Path guided motion synthesis for Drosophila larvae*#
2023-11-06JunjunCHENYijunWANGYixuanSUNYifeiYUZiaoLIUZhefengGONGNengganZHENG
Junjun CHEN ,Yijun WANG ,Yixuan SUN ,Yifei YU ,Zi’ao LIU ,Zhefeng GONG,4,5 ,Nenggan ZHENG†‡,3
1Research Institute of Basic Theories,Zhejiang Lab,Hangzhou 311121,China
2School of Rehabilitation Sciences and Engineering,University of Health and Rehabilitation Sciences,Qingdao 266114,China
3Qiushi Academy for Advanced Studies,Zhejiang University,Hangzhou 310007,China
4Department of Neurobiology and Department of Neurology of Second Affiliated Hospital,Affiliated Mental Health Center,Zhejiang University School of Medicine,Hangzhou 310058,China
5NHC and CAMS Key Laboratory of Medical Neurobiology,MOE Frontier Science Center for Brain Research and Brain-Machine Integration,School of Brain Science and Brain Medicine,Zhejiang University,Hangzhou 310058,China
Abstract: The deformability and high degree of freedom of mollusks bring challenges in mathematical modeling and synthesis of motions.Traditional analytical and statistical models are limited by either rigid skeleton assumptions or model capacity,and have difficulty in generating realistic and multi-pattern mollusk motions.In this work,we present a large-scale dynamic pose dataset of Drosophila larvae and propose a motion synthesis model named Path2Pose to generate a pose sequence given the initial poses and the subsequent guiding path.The Path2Pose model is further used to synthesize long pose sequences of various motion patterns through a recursive generation method.Evaluation analysis results demonstrate that our novel model synthesizes highly realistic mollusk motions and achieves state-of-the-art performance.Our work proves high performance of deep neural networks for mollusk motion synthesis and the feasibility of long pose sequence synthesis based on the customized body shape and guiding path.
Key words: Motion synthesis of mollusks;Dynamic pose dataset;Morphological analysis;Long pose sequence generation
1 Introduction
All animals,whether vertebrates or invertebrates,interact with the environment mainly through a variety of motions that include complex and subtle spatialtemporal features.Modeling the motion dynamics and synthesizing the realistic motions of animals have great significance in many industrial applications,such as computer animation (Holden et al.,2016;Mourot et al.,2022),game production (Busso et al.,2005;Eberly,2007;Sha et al.,2021),and biomimetic robots (Okajima et al.,2018;Dong et al.,2021).Mollusks such asCae‐norhabditis elegans,caterpillar,andDrosophilalarva have received increasing attention in both scientific research and industrial engineering due to their unique features including deformability and high degree of freedom (DOF).However,compared with mammals,especially humans,few studies on the motion synthesis of mollusks have been reported.
Animal motions are typically depicted by pose sequences for mathematical analysis and synthesis(Ionescu et al.,2014;Li RL et al.,2021;Negrete et al.,2021;Shooter et al.,2021).Each pose consists of a set of points and edges that represent the joints and skeletons of animals,respectively.Traditional analytical models (Sok et al.,2007;Yin et al.,2007,2008;Coros et al.,2010;Liu LB et al.,2010) simplify the mechanical constraints of poses by regarding the skeletons as rigid and restricting the DOF of joints to construct the dynamic equations.Generally,the pose sequence of a specific motion pattern is decomposed into several consecutive states whose dynamic features are modeled by proportional derivative (PD) controllers,and the transitions between states are determined by a finite state machine.The analytical model is physically interpretable and allows the virtual agent to interact with the environment such as walking on ice and climbing stairs.However,the drawbacks of the analytical model are noticeable.First,PD controllers are simplified mechanical models of complex biological neuromuscular actuation systems,and easily lead to stiff and unnatural motions.Second,the motion decomposition and the PD controller parameters are generally bound to specific actions,so it is hard to develop a universal model to cover multiple motion patterns.Finally,the analytical model assumes rigid skeletons of animals and cannot apply to mollusks.The motion synthesis of mollusks is more complicated than that of mammals due to the extremely high DOF.One feasible method is to model the mollusk body with several end-to-end springs to reduce the DOF(Yekutieli et al.,2005).
Apart from the analytical models,statistical models using machine learning methods are widely applied to motion synthesis,and learn the underlying distribution of pose sequences from plenty of samples regardless of the physical mechanisms.Bayesian statistical models,such as linear dynamic systems (LDSs)(Kalman,1960;Pavlovic et al.,2000) and hidden Markov models (HMMs) (Busso et al.,2005;Yu,2010;Lehrmann et al.,2013;Zhao and Ji,2018),explore dynamic process of motions by modeling the transitions between adjacent hidden states.However,LDSs describe dynamic process with a simple linear model,whereas the computational complexity of HMMs grows exponentially with the model capacity increasing.Furthermore,both models have state transition assumptions,which are not always consistent with real motion dynamics.Recently,deep neural networks (DNNs) have been applied to motion analysis and achieved remarkable success due to their powerful data fitting ability without extra assumptions (Dang et al.,2019;Sha et al.,2021;Zhang DJ et al.,2021).Various models,such as the convolutional neural network (CNN) (Li C et al.,2018;Li YR et al.,2019;Mao et al.,2019;Liu XL et al.,2021),recurrent neural network (RNN) (Fragkiadaki et al.,2015;Jain A et al.,2016;Ghosh et al.,2017;Martinez et al.,2017;Pavllo et al.,2018;Aksan et al.,2019;Guo and Choi,2019;Wang et al.,2019),and Transformer (Aksan et al.,2021;Bhattacharya et al.,2021;Li RL et al.,2021),have been implemented in pose synthesis tasks.Compared to analytical and statistical models,DNNs have some impressive advantages,although they demand more training samples and more time for model optimization.First,deep motion synthesis models do not assume a rigid skeleton and can apply to both mammals and mollusks.Second,the superior model capacity of DNNs makes it possible to synthesize various motion patterns with a single end-to-end model,which improves the model generalization and simplifies the computational process.Furthermore,new optimization methods such as generative adversarial network (GAN) have been proposed to allow the model to generate more realistic pose sequences and even new motions not present in the dataset (Barsoum et al.,2018;Kundu et al.,2019;Jain DK et al.,2020;Li MS et al.,2020;Cui and Sun,2021).
Although the pose synthesis model based on DNNs has achieved impressive success,there are still some issues to be addressed.First,generating realistic motions remains a significant challenge due to the anisotropy and diversity of spatial-temporal data.Sequential models,such as RNN,focus on exploring temporal dynamics,but process spatial features via simple linear layers,which may lead to unrealistic body shapes.Yan et al.(2019) proposed the spatial-temporal graph convolutional network (STGCN) to model local spatialtemporal features and achieved better performance than traditional sequential models.Second,generating a long pose sequence is another challenge for DNN models (Aksan et al.,2021;Mourot et al.,2022).Sequential models like RNN are prone to suffer from error accumulation and regression to the mean,which may cause synthesized motions to freeze (Li RL et al.,2021).Third,compared with motion synthesis of mammals,mollusks are less studied and large-scale mollusk pose datasets have never been reported.Considering the high DOF and deformability of mollusks,the performance of DNNs in motion synthesis tasks remains to be studied.
We propose a deep motion synthesis model to generate long pose sequences ofDrosophilalarvae given the initial poses and the guiding path.(1) We construct a large-scale dynamic pose dataset ofDro‐sophilalarvae for model training.(2) We propose the Path2Pose model to synthesize fixed-length pose sequences that are joined smoothly to the initial poses and match the guiding path.(3) We use the welltrained Path2Pose model to synthesize long pose sequences via recursive generation and concatenation,which solves the error accumulation problem.A series of evaluation metrics based on biological morphology and machine learning demonstrate that our novel model generates highly realistic pose sequences and achieves state-of-the-art performance compared with classic neural network models.
2 Methods
2.1 Dataset construction
We employed DNNs to estimateDrosophilalarval poses from video images and constructed a large-scale dynamic pose dataset.Briefly,a portion of the video images were manually annotated to train a semantic segmentation model and a pose estimation model,which were then used to estimate the poses in the remaining video images.A recursive refinement strategy was designed to retrain the models to improve the estimation accuracy and minimize the demand for manually annotated images.
2.1.1 Video acquisition
We labeled theDrosophilalarval muscles with GCaMP,a genetically encoded calcium indicator,and recorded their motions under a fluorescence microscope.The brightness of muscles varied with the degree of their contraction under the microscope,which makes the body segments distinguishable.All experimental subjects were first-instar larvae with body length ranging from 0.8 to 1.2 mm.Each subject was placed in a 5-mm-diameter container filled with water for free movement.The motions ofDrosophilalarvae were recorded at 100 frames per second (FPS) using a highspeed camera under the fluorescence microscope.The video resolution varied between 2000×2000 pixels and 2304×2000 pixels depending on the experimental session.Each subject was recorded for a limited time because of the photo-bleaching phenomenon.Only the active subjects were picked for the experiments and recorded until they stopped moving for >2 min.Considering theDrosophilalarvae move quite slowly,we down sampled the raw videos to 3 FPS to accelerate the motion dynamics.
2.1.2 Manual annotation
We uniformly sampled a subset of images for manual annotation from the down sampled videos at a sampling rate of 1:30.The first-instarDrosophilalarvae had 12 body segments,of which the last two segments close to the tail were indistinct.Therefore,we used 22 keypoints,including 1 head point,1 tail point,and 20 body points,to construct the larval pose,and divided the body into 11 segments.Each pose contained two-dimensional (2D) coordinates of the 22 keypoints.Three well-trained technicians spent a total of >60 h annotating the selected images via an open-source image annotation tool (labelme) and finally obtained about 2000 pose-image pairs.
2.1.3 Segmentation and pose estimation
We implemented a semantic segmentation model named Mask R-CNN (He et al.,2017) to estimate the body contours and draw the bounding boxes for each video image.Then,a pose estimation algorithm based on a high-resolution model (HRNet) (Cao et al.,2019;Sun et al.,2019) was employed to estimate the positions of the 22 keypoints for each cropped image.
2.1.4 Refinement and smoothing
We developed a recursive refinement method to improve the accuracy of pose estimation and minimize the demand for manually annotated data as much as possible.First,we used principal component analysis(PCA) to extract the top five principal components(PCs) of the estimated poses and detected the outliers of these PCs using a sequential anomaly detection algorithm (PersistAD,Anomaly Detection Toolkit).Then,the images with anomalies were manually annotated and merged with the previously annotated data for the second model training.This refinement operation was repeated several times until the estimated poses were accurate enough to depict larval motions.Finally,because the poses were estimated from individual images independently,all keypoints were temporally smoothed to eliminate oscillation.
2.1.5 Evaluation
The mean per-joint position error (MPJPE) is a commonly used metric to evaluate the accuracy of estimated poses (Ionescu et al.,2014;Li RL et al.,2021).In this work,we normalize it to the body length ofDrosophilalarva to compute a more intuitive relative error.For a frame of poset,the normalized mean per-joint position error (NMPJPE) was computed using the following equation:
whereNtis the number of keypoints,Ltis the larval body length,which is the sum of all body segment centerlines,pestandpannare the positions of the estimated and manually annotated keypoints,respectively,and ‖ · ‖2represents the L2 norm.NMPJPE was applied to the evaluation of not only the estimated poses,but also the synthesized movement path in the following analysis.
2.2 Path2Pose model
As illustrated in Fig.1,we design a deep generative neural networkGnamed Path2Pose to synthesize the pose sequence ofDrosophilalarva given an initial pose sequence and a guiding path.The Path2Pose model should ensure a seamless transition from the initial sequence to the synthesized sequence,while maintaining the consistency between the guiding path and the larval head movement path.An adversarial loss and a reconstruction loss are introduced to improve the similarity (to the real pose sequences) and the movement path accuracy of the synthesized pose sequences,respectively.The Path2Pose model is trained with our constructed DLPose dataset.

Fig.1 Architecture of the Path2Pose model including a generative model and the loss functions.The generative model takes the initial poses and the guiding path as inputs and synthesizes the subsequent pose sequence matching the guiding path.The loss functions consist of a conditional adversarial loss and a path reconstruction loss
2.2.1 Generative model
In the Path2Pose model,three inputs are fed into the generative model including an initial pose sequenceand a Gaussian noise vectorz,whereKandNare the frame numbers of the initial poses and the guiding path,respectively.As a result,the generative modelGoutputsNframes of the synthesized posesSuperscripts of the variables represent the global time points to illustrate the temporal relationship.As spatial-temporal data,the pose sequence has three dimensions including a temporal dimension relating to the sequence length,a spatial dimension with regard to 22 keypoints,and a feature dimension containing the coordinates of individual keypoints.
First,the initial pose sequencePiniis processed in an RNN-based pose encoder to extract its intrinsic spatial-temporal features,such as the larval body shape and the historical dynamics.The last hidden state of the RNN and the Gaussian noisezcreate temporal extensions by duplicating themselves along the temporal dimension.Then they are joined to the guiding pathXgalong the feature dimension to construct a composite vector sequenceC=[cK+1,cK+2,…,cK+N].Next,a path encoder,composed of a ResNet and a multi-head self-attention (MHSA) network,is designed to fuse the information inCand obtain an intermediate state sequenceS=[sK+1,sK+2,…,sK+N].Specifically,the ResNet processes each composite vectorci(i=K+1,K+2,…,K+N) independently,while the MHSA network integrates information along the temporal dimension.Then the last frame of the initial pose sequenceis extended temporally and joined to the composite vector sequenceCand the intermediate state sequenceSalong the feature dimension to obtain a hidden state sequenceH=[hK+1,hK+2,…,hK+N].This skip connection prevents the model from omitting important previous information and directly uses the most relevant pose to synthesize the subsequent pose sequence.Finally,the hidden state sequenceHis fed into a spatialtemporal pose decoder (STPD) to generate the final pose sequencePsyn.Inspired by STGCN (Yan et al.,2019),we propose a novel attention-to-convolution network (AttnCnNet) by replacing the spatial graph convolutional layer of the STGCN with MHSA layer and duplicating the temporal convolutional layer twice.Specifically,each framehi(i=K+1,K+2,…,K+N)ofHis fed into the MHSA layer independently to decode the spatial features,while the subsequent convolutional layers decode the temporal dynamics for individual keypoints in the temporal dimension.Compared with the GCN,the MHSA layer explores the global relationship of keypoints in a pose instead of the local one,which allows it to better model the spatial features.
2.2.2 Optimization
The generative modelGis prone to suffer from regression to the mean when optimized by either L1 or L2 loss,resulting in stiff movements.Therefore,the adversarial loss (Goodfellow et al.,2014) is implemented to optimizeGdue to its impressive improvement in generative tasks.In addition,a path reconstruction loss is introduced to constrain the head movement path of theDrosophilalarvae.
The discriminator in the Path2Pose model is implemented to improve the similarity of the synthesized poses to the real ones.As illustrated in Fig.1,the synthesized pose sequencePsynis temporally joined to the initial sequencePinito obtain the complete pose sequencePc,which containsK+Nframes and 22 keypoints in each frame.Next,the spatial dimension ofPcis reconstructed in preparation for the three-dimensional(3D) convolution operation according to the topology of theDrosophilalarval pose as shown in Fig.2.Specifically,the 22 keypoints are numbered clockwise and rearranged into two rows,so that the topologically adjacent keypoints are close to each other.As a result,the reconstructedPchas a four-dimensional (4D) spatialtemporal structure,including one temporal dimension,two spatial dimensions,and one feature dimension.The corresponding real pose sequences ofPsynare processed in the same way.Both the real and synthesized pose sequences are fed into a discriminatorDbased on a 3D CNN (Ji et al.,2013;Carreira and Zisserman,2017) to compute the probability.Note that GAN usually suffers from unbalanced training between the generator and the discriminator,resulting in gradient vanishing during the training process.Therefore,we add a spectrum normalization layer after each convolutional layer to make the discriminator 1-Lipschitz continuous (Miyato et al.,2018),which could prevent gradient from vanishing effectively.

Fig.2 Rearrangement of the 22 keypoints of the Drosophila larval pose
The discriminatorDis optimized using the following equation:
whereRis the real pose sequence sampled from the DLPose dataset,preal,based on the initial pose sequencePiniand the guiding pathXg,andzis the noise with a Gaussian distributionpnorm.The loss of the generative modelGconsists of an adversarial loss from the discriminatorDand an L2 reconstruction loss between the guiding path and the synthesized head movement path.
whereFtis the head movement path of the synthesized poses andαis the predefined gain of the path reconstruction loss.
2.2.3 Implementation details
In our experiments,the lengths of the initial pose sequence and the guiding path are set toK=5 andN=35,respectively.The long sequences in the DLPose dataset are first divided into a training set and a test set,and then split into short segments of 40 frames with a sliding window (window size=40,step=10).The coordinates of each segment are adjusted to ensure that the head point of the first pose lies at the origin of coordinates.Then,the coordinates of all sequences are normalized between -1 and 1 with the same scale ratio.The gain of the path reconstruction loss is set to 0.1.The Path2Pose model is trained with a batch size of 256 using an Adam (Kingma and Ba,2015) optimizer (β1=0.5,β2=0.99).The initial learning rates of the generator and the discriminator are set to 1e-4 and 5e-4,respectively,and an exponential decay rule is applied to them to stabilize the model training.The model is trained on a Tesla V100 graphics processing unit (GPU) for up to 20 000 epochs until no significant performance improvement.
2.3 Morphological metrics
Inspired by the eigenworms (Stephens et al.,2008),we designed two morphological metrics,eigenwaves and eigenbodies,to depict the peristaltic wave and the body posture ofDrosophilalarva.TheDrosophilalarva crawls by contracting and relaxing its body segments sequentially,which results in peristaltic wave passing through the body periodically.Therefore,the peristaltic wave can be depicted by a feature vector composed of body segment lengths.For eigenwaves,the lengths of all body segments are measured to construct a length vector,which is normalized to the body length:
whereli(i=1,2,…,11) is the measured length of theithbody segment.
PCA is applied to the normalized length vectors across all pose frames to obtain the PCs,which are called eigenwavesAs for the eigenbodies,a series of angles between the adjacent body segments are computed to construct the angle vectorand PCA is directly applied toVAto obtain the eigenbodies
Both eigenwaves and eigenbodies are employed to evaluate the similarity of our synthesized poses to the real ones.First,the real poses in the DLPose dataset are used to train the PCA and calculate the real eigenwaves/eigenbodies.Then,the synthesized poses are projected into the same eigenspace with the trained PCA to obtain the synthesized eigenwaves/eigenbodies.Finally,we explore the relationship between the real and the synthesized eigenwaves/eigenbodies to evaluate the similarity of the synthesized poses to the real ones.
2.4 Evaluation metrics
To compare the similarity of the pose sequences synthesized by different models to the real ones,a binary classifier based on 3D CNNs is implemented to calculate three evaluation metrics including classification accuracy,false positive (FP) rate,and Fréchet discriminative distance (FDD) in two different classification tasks.
Classification accuracy and FP rate:In the first classification task,a binary classifier is used to distinguish the real pose sequences from the synthesized ones for different models.The classification accuracy is calculated with the test data after 500 training epochs.Generally,the superior model tends to have lower accuracy than the other models.The FP rate is defined as the ratio of the number of misclassified synthesized samples to that of all the synthesized samples,i.e.,the probability that the classifier regards the synthesized samples as the real ones.Therefore,the generative model with better performance tends to have a higher FP rate.
FDD:Inspired by the Fréchet inception distance(FID)—a metric to evaluate the quality of synthesized images (Heusel et al.,2017)—we propose FDD to quantify the similarity of the synthesized pose sequences to the real data.In the second classification task,a binary classifier is employed to distinguish the real pose sequences from a collection of synthesized ones originating from multiple models.The classifier maps the pose sequence to a high-dimensional feature vector and calculates the probability with the feature vector in the output layer.We remove the output layer of the well-trained classifier and use it to project the pose sequences into the feature vector space.The FDD is defined as the Fréchet distance between the two sets of feature vectors of the real and the synthesized samples:
whereuandΣare the mean and covariance matrices of the feature vectors,respectively.Compared to FID,the FDD classifier directly distinguishes the real and the synthesized samples,which makes the FDD more sensitive to the difference between them.
2.5 Long pose sequence synthesis
Some complex motion patterns ofDrosophilalarvae,such as turning,generally last for relatively long time and cannot be completely depicted with the individual short sequences synthesized by the Path2Pose model.Therefore,we use the well-trained model to synthesize the long pose sequence by generating and joining short sequences recursively.Given an initial pose sequence ofKframes and the subsequent long guiding path,the long path is first split into several segments ofNnon-overlapping frames.Then the initial sequence and the first guiding path are fed into the Path2Pose model to synthesize a pose sequence of which the lastKframes serve as the initial poses of the second guiding path for the next generation.The coordinates of both the initial poses and the guiding path are adjusted before each generation to make sure that the head point of the first initial pose lies at the origin of coordinates.In this way,a series of short pose sequences are synthesized recursively.Finally,all the synthesized short sequences are joined end-to-end to obtain a long pose sequence.
3 Results
3.1 DLPose dataset
We recorded the videos of 51Drosophilalarvae with a total length of 5.1 h.The raw videos were then down sampled to 3 FPS to accelerate the motion dynamics.To ensure the continuous movement ofDro‐sophilalarvae,we manually cut out the frame sequences when the subjects had been still for >2 s,and finally obtained 61 644 frames of video images,which were divided into 165 clips.The videos captured most of the natural motion patterns ofDrosophilalarvae including straight locomotion,turns,and head sweeps.The pose,composed of 22 keypoints,was estimated from each video image independently and smoothed temporally as described in Section 2.Therefore,the DLPose dataset was composed of a series of video clips and the paired pose sequences.The constructed poses precisely depicted the spatial-temporal features ofDrosophilalarval motions,such as peristaltic waves during straight locomotion (Fig.3,movie 1) and multiple body postures during turning (Fig.S1,movie 2).The NMPJPE of the DLPose dataset was 0.0105±0.0241,which indicated that the average estimated error of an individual keypoint was only 1.05%±2.41% of the body length.Most public animal datasets were composed of discrete images,which contained only static features such as body postures,but no motion dynamics.To our knowledge,the DLPose dataset was the first large-scale dynamic pose dataset for mollusks that contained multiple motion patterns and supported training of the deep motion synthesis model.
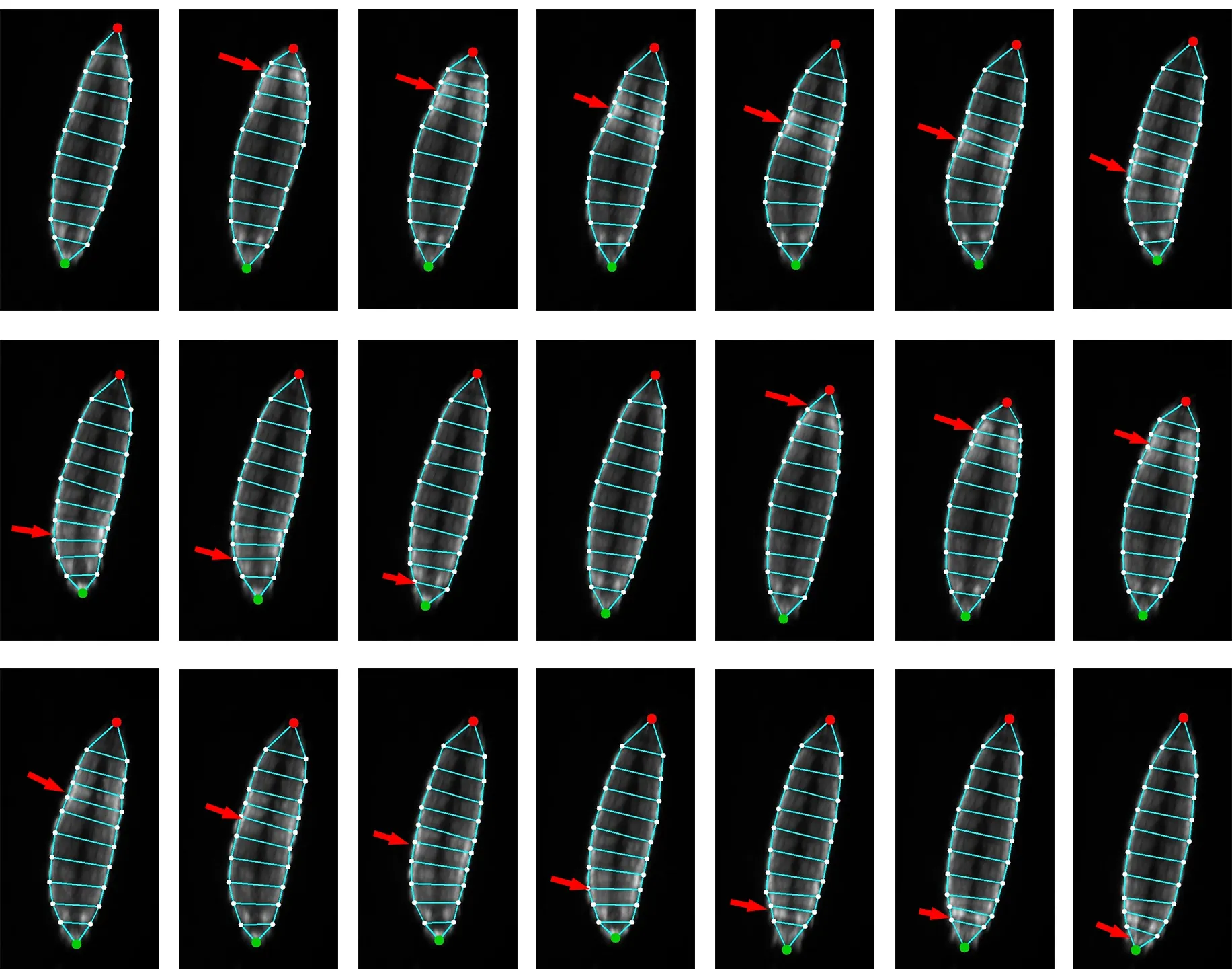
Fig.3 An estimated pose sequence in the DLPose dataset.Raw video images of 2000×2000 pixels are cropped to 330×624 pixels for demonstration.The pose sequence depicts a Drosophila larva moving forward with the peristaltic wave (red arrow) passing through its body periodically.The peristaltic wave propagates from the tail (red point) to the head (green point) in a crawling cycle
3.2 Short pose sequence synthesis
We synthesized 1000 pose sequences (35 frames per sequence) with the Path2Pose model given the initial poses and the guiding paths sampled from the DLPose dataset.Each synthesized sequence has its counterpart in the dataset.As spatial-temporal data,the pose sequence has both static and dynamic features.On one hand,static features are related to the keypoint distribution of the individual pose.That is,the 22 keypoints should lie on a reasonable hyperplane to form a realistic and natural body shape ofDrosophilalarva.TheDrosophilalarva has many typical motion patterns,such as straight locomotion (Figs.4a and 4b,movie 3),head sweeps (Fig.S2,movie 4),and turns,resulting in a variety of body postures and static features.On the other hand,the dynamic features refer to the temporal evolution process of a series of keypoints.The peristaltic wave is a typical dynamic motion feature ofDrosophilalarva,which is usually accompanied by longitudinal and lateral contraction of local keypoints.The peristaltic wave of the synthesized pose sequence (Fig.4b) is similar to that of the real data (Fig.4a) in terms of the wave appearance and the propagation process.In addition to the peristaltic wave,we analyze the dynamics of the head and the tail points.The synthesized head movement path is highly identical with the guiding path in Fig.4c,thanks to the path reconstruction loss of the Path2Pose model.The Pearson correlation coefficient between them is 0.9956±0.0460 and the NMPJPE is 0.003 715±0.002 357,which indicates that the average error of individual head point equals 0.3715%±0.2357% of the body length.The tail movement is another important dynamic feature because the forward locomotion always starts from the tail.As illustrated in Fig.4d,the tail travel distance normalized by larval body length shows obvious periodicity during forward locomotion for the real and the synthesized samples.The rapid rise of the travel distance curve indicates the tail’s forward contraction at the beginning of a crawling cycle,and a slight decline may occur because of the tail’s slip on the surface.The plateau represents a phase when the anterior body segments move forward sequentially.We calculate the Pearson correlation coefficients between the real and the synthesized travel distances for both the head and the tail points,respectively (Fig.4e).The synthesized tail movement is not strictly identical to the real data compared to the head movement,because it is not restricted in the path reconstruction loss of the Path2Pose model.However,most synthesized samples present significant similarity to the real ones in terms of the tail travel distance,which indicates that the Path2Pose model captures the main dynamic features of the tail.
3.3 Morphological evaluation
To study the physical meaning of the proposed morphological metrics,theDrosophilalarval body segments from the tail to the head are numbered from 1 to 11.The top four eigenwaves and top four eigenbodies,which explain more than 90% and 70% of total variance,respectively (Fig.S3),are closely related to the propagation of the peristaltic wave and the bending state of the larval body,respectively (Fig.S4).For example,the trough and peak of the first eigenwave (eigenwave 1)correspond to the peristaltic wave located at the third and ninth body segments,respectively.The first eigenbody (eigenbody 1) becomes positive when the body bends to the right (frames 10,22,and 26) and negative when the body bends to the left.The lower-ranking metrics,such as eigenwave 4 and eigenbody 4,have higher frequencies and smaller amplitudes,indicating that the low-ranking metrics may explain the high-frequency and subtle components.
Considering that the top eigenwaves and eigenbodies are closely related to the states of peristaltic wave and body posture,respectively,we use them to evaluate the similarity of our synthesized pose sequences to the real data in terms of the peristaltic wave and the body posture.We extract the top four eigenwaves and top four eigenbodies from individual pose sequences and compare each metric seperately between the real and the synthesized pose sequences.The Pearson correlation coefficient is used to quantify the similarity of metric.As illustrated in Figs.5a and 5b,the morphological metrics of the real and the synthesized pose sequences are generally linearly dependent.Fig.5c shows the proportion of samples with significant Pearson correlation coefficients for each metric,which indicates that most samples show significant correlation in the top eigenwaves and eigenbodies (p<0.05).The distribution of correlation coefficients in Fig.5d shows that the higher-ranking metric tends to have a stronger correlation than the lower-ranking one,which indicates that the Path2Pose model learns key motion features from the real data and concurrently generates various details.
3.4 Comparison with other models
We compare the performance of the Path2Pose model with those of the traditional neural network models including CNN (Liu XL et al.,2021),RNN(Fragkiadaki et al.,2015),and fully connected networks.In the CNN and LSTM models,the initial pose sequences are first encoded using a vanilla RNN and then fed into the main network with the guiding paths to generate the subsequent sequences.The mode-adaptive neural network (MANN) (Zhang H et al.,2018) is a classical sequence-to-sequence model constructed using a fully connected network,in which eigenwave 1 and eigenbody 1 serve as the input of the gating network to update the parameters of the motion prediction network.All the above models are optimized by the pose reconstruction loss,which is the mean squared error between the real and the synthesized pose sequences.The Path2Pose model tends to synthesize more realistic poses with smoother body contours and more natural peristaltic waves than the other models (Fig.S5).Three metrics,including classification accuracy,FP rate,and FDD,are used to quantify the model performance (Table 1).The Path2Pose model shows a lower classification accuracy and a higher FP rate than the traditional models,which means that the classifier has more difficulty in distinguishing the synthesized samples of the Path2Pose model from the real data than those of the other models.FDD is a similarity metric that quantifies the distribution distance between the real and the synthesized data.The Path2Pose model has the lowest FDD among the traditional models,which means that its synthesized samples are closer to the real data in the feature space.
To evaluate the performance of the AttnCnNet in the Path2Pose model,we design the variants of the Path2Pose model by replacing the AttnCnNet with RNN and GCN modules,while the other modules remain unchanged.All models are trained for 20 000 epochs and then employed to synthesize 1000 pose sequences for evaluation.As illustrated in Table 2,AttnCnNet has better results than the RNN and GCN modules in three metrics,which proves that AttnCnNet can synthesize better pose sequences than the traditional sequence-to-sequence models.

Table 2 Synthesized results of AttnCnNet compared with the variants of Path2Pose model
3.5 Long pose sequence synthesis
Pose sequences synthesized by the Path2Pose model are limited by the fixed short length and hardly depict complicated and continuous motions ofDro‐sophilalarvae,which limits the practical application of the Path2Pose model.Therefore,we use well-trained model to synthesize long pose sequences in a recursive way as described in Section 2.Fig.6 (movie 5)shows a synthesized long pose sequence,in which a larva makes a left turn by changing the locomotion direction twice.The long sequence,joined with four short segments,consists of 145 pose frames and is down sampled for the sake of demonstration.More synthesized samples are shown in Figs.S6 and S7(movies 6 and 7).There are two challenges in the long pose sequence synthesis task—smooth transition between segments and error accumulation.On one hand,the initial pose sequence provides information about the larval body shape and the historical motion to the Path2Pose model,which contributes to the natural transition between segments.The length of the initial pose sequence is the result of a trade-off between the generation similarity and the computational cost.On the other hand,there is no significant error accumulation in terms of path accuracy and generation similarity in our experiments.As illustrated in Fig.7a,the head movement path of the synthesized sequence strictly matches the guiding path among all four segments.The NMPJPE of the path shows no significant difference across segments (Fig.7b,ANOVA,p=0.9311),which indicates that the path error does not accumulate with an increase in the sequence length.In addition,we evaluate the generation similarity of each joined segment with classification accuracy and FP rate.The results in Figs.7c and 7d show that there is no significant difference in terms of the two metrics across four segments (ANOVA:classification accuracy,p=0.2028;FP rate,p=0.5143),which indicates that the sequence length has little impact on the similarity of the synthesized poses to the real ones.

Fig.6 A long pose sequence composed of four recursively synthesized segments.The head movement paths of individual segments are labeled by different colors
4 Discussion
The construction of a pose dataset is typically a laborious task that involves the acquisition and extraction of a vast amount of motion data.Human poses are typically recorded with motion capture technology,which is infeasible for mollusks.We employ DNNs to estimate the poses ofDrosophilalarvae from recorded videos.Considering that DNNs demand plenty of manually annotated samples for training,we propose a recursive refinement strategy to annotate the incorrectly estimated images and retrain the models until the estimation error is sufficiently small.This method enables the model to learn new knowledge,which is not mastered,and minimizes the demand for manually annotated images as soon as possible.To our knowledge,the DLPose dataset is the first public dynamic pose dataset for mollusks.Note that the estimated poses in the DLPose dataset are 2D data.Therefore,only the horizontal components of motions are captured while some vertical motions,such as hunching,cannot be depicted precisely.
The generator of the Path2Pose model is modified from the pose/video prediction models in computer vision (Fragkiadaki et al.,2015;Martinez et al.,2017),which originally generate the subsequent sequences given several initial frames.In the Path2Pose model,the guiding path is introduced as the second conditional input to allow users to customize the head movement path ofDrosophilalarva.The adversarial loss and the path reconstruction loss are introduced to improve the similarity of synthesized poses to the real ones and the accuracy of paths,respectively.We implement three methods to solve the gradient vanishing problem of the GAN.First,the last frame of the initial sequence is directly fed into the spatialtemporal decoder to provide the closely relevant pose information.We prove that this skip connection can accelerate the model convergence in our experiments.Second,our discriminator is constructed using a simple 3D CNN instead of the more powerful neural networks like GCN to balance the performances of the generator and the discriminator (Liu C et al.,2022).Finally,attaching a spectrum normalization layer after each individual convolutional layer in the discriminator to make it 1-Lipschitz continuous is probably the most effective method to prevent the gradient vanishing.
Theoretically,the Path2Pose model allows users to arbitrarily customize the initial pose sequence and the guiding path sampled from the DLPose dataset.But in practice,the two inputs of the Path2Pose model,the initial pose sequence and the guiding path,should be carefully selected to guarantee their natural and reasonable motion semantics.For example,an initial pose sequence of forward crawling paired with a backward guiding path implies an unnatural orientation change that is too abrupt,leading to a collapse of the pose synthesis.In our current work,guiding path must be the real head movement path ofDrosophilalarvae,because the Path2Pose model is trained with the real paths from the DLPose dataset.We will extend the versatility of the model in the future to make it compatible with hand-drawn guiding paths,which are more continuous and smoother than the real movement paths.
5 Conclusions
In this paper,we propose an end-to-end motion generative model to synthesize long pose sequences ofDrosophilalarvae with various motion patterns and allow users to customize the body shape and the movement path.First,we construct a large-scale dynamic pose dataset ofDrosophilalarvae to support model training.Then the Path2Pose model is proposed to synthesize the short pose sequence given the initial poses and the guiding path sampled from the dataset.Finally,the well-trained model is employed to synthesize the long pose sequences by recursively generating and joining short sequences.The evaluation analysis results show that the Path2Pose model synthesizes highly realisticDrosophilalarval motions in terms of morphology and achieves better performance than the traditional models.This work demonstrates the feasibility of a deep generative model in the motion synthesis of mollusks.In the future,we will focus on more realistic pose generation ofDrosophilalarva based on hand-drawn guiding paths.
Contributors
Nenggan ZHENG and Junjun CHEN conceived the idea and designed the research.Zhefeng GONG and Yixuan SUN conducted the experiments and recorded the videos ofDrosophilalarval motions.Yifei YU and Zi’ao LIU preprocessed the video data.Junjun CHEN drafted the paper.Zhefeng GONG and Nenggan ZHENG helped organize the paper.Junjun CHEN and Yijun WANG revised and finalized the paper.
Compliance with ethics guidelines
Nenggan ZHENG is a corresponding expert ofFrontiers of Information Technology &Electronic Engineering,and he was not involved with the peer review process of this paper.Junjun CHEN,Yijun WANG,Yixuan SUN,Yifei YU,Zi’ao LIU,Zhefeng GONG,and Nenggan ZHENG declare that they have no conflict of interest.
Data availability
The source code and data used in this study are openly available in Github at https://github.com/chenjj0702/Path2Pose.git.
List of supplementary materials
Fig.S1 Estimated pose sequence in the DLPose dataset depictingDrosophilalarval turning motion
Fig.S2 Pose sequences depictingDrosophilalarval head sweeps:(a) real pose sequence from the DLPose dataset;(b) synthesized pose sequence with the same initial poses and guiding path.The guiding and synthesized movement paths are represented by the blue and red lines,respectively
Fig.S3 Cumulative variance of the principal components(PCs) for eigenwaves (a) and eigenbodies (b)
Fig.S4 Morphological analysis for eigenwaves and eigenbodies:(a) typical pose frames (top panel) and top four eigenwaves (bottom panel) of a pose sequence (peristaltic wave position is labeled by the red arrow);(b) typical pose frames (top panel) and top four eigenbodies (bottom panel)of a pose sequence
Fig.S5 Pose sequence synthesized by RNN (a),MANN (b),and Path2Pose (c) models
Fig.S6 Synthesized long pose sequence joined with four segments depictingDrosophilalarval forward locomotion
Fig.S7 Synthesized long pose sequence joined with four segments depictingDrosophilalarval head sweeps and turning
杂志排行
Frontiers of Information Technology & Electronic Engineering的其它文章
- Correspondence:A low-profile dual-polarization programmable dual-beam scanning antenna array*#
- Correspondence:Uncertainty-aware complementary label queries for active learning∗
- Wideband and high-gain BeiDou antenna with a sequential feed network for satellite tracking
- Synchronization transition of a modular neural network containing subnetworks of different scales*#
- RFPose-OT:RF-based 3D human pose estimation via optimal transport theory∗
- Attention-based efficient robot grasp detection network∗
