基于银行单位资产损失分布的存款保险定价研究

张金宝

(北京第二外国语学院 经济学院,北京 100082)

0 引言

我国于2015年5月1日正式实行存款保险制度。国务院颁布的《存款保险条例》决定实行基准费率和风险差别费率相结合的存款保险费率。目前执行的费率平均约为被保险存款的1.6个基点左右,并没有体现出不同银行的风险差别,这意味着现有存款保险定价方法仍不能为确定合理的风险费率水平提供足够的理论支撑。存款保险定价通常有两种范式:一种是基于预期损失的定价方法[1],另一种则是基于期权理论的定价方法[2]。但这两种范式只适用于上市银行和少量获得权威的外部评级的商业银行,无法适用于国内近四千家参保银行中绝大多数的中小银行,从而形成实证研究中的空白,这正是当前存款保险费率厘定所面临的困境。本文将尝试建立一个更符合我国国情的存款保险定价方法。

1 文献研究回顾

1.1 研究回顾

基于期权理论的存款保险定价方法由MERTON[2]提出。MERTON认为:存款保险可看成是一个看跌期权,这个看跌期权的标的就是银行的资产价值,执行价格是保险到期后被保险存款的本息和。用看跌期权的价值除以期初存款的额度,就得到存款保险的费率。基于期权的定价方法需要借助银行股票的市场价格估计两个关键的参数:银行的资产价值和波动率[3]。在此范式下,学者们开展了大量的扩展性研究[4-7]。但因需要银行的股价数据,实证研究均针对的是上市银行。

另一种基于预期损失的定价范式由LAEVEN[1]提出。该方法将银行破产造成的不能全部支付存款者本息的现象看成银行对存款者的违约行为。用破产时银行资产的损失除以被保险的存款,就得到了存款保险费率。该方法需确定两个关键参数:一是银行的破产概率,一般是根据权威评级机构(如标准普尔等)对银行评级所积累的历史数据来估算[1]。另一个参数是被保险存款的违约损失率。LAEVEN通过贷款的违约损失率和存贷比来估算。张金宝和任若恩[8]在预期损失范式下进行了扩展性研究。此外,也有学者从维持保险基金平衡的角度讨论存款保险定价问题[9],但尚在理论探讨阶段,未见有实证研究发表。

1.2 研究评述

基于期权理论的定价方法只能用于上市银行。预期损失定价方法虽然适用于非上市银行,但需要外部评级数据来估算银行的破产/违约概率,而目前只有为数不多的银行公布过它们获得的来自标普、穆迪等有影响力的评级公司的信用级别。国内虽有评级公司进行银行的信用评级,但积累的历史数据时间较短,且国内鲜有银行倒闭发生,因而很难依据国内的评级数据测算银行的破产概率。参保银行中绝大多数银行是未上市或未获得外部评级的中小银行。问题在于,中小银行的风险往往相对较高,这恰恰是存款保险定价应该重点关注的对象。因此需要研究一种适用范围较广的存款保险定价方法。

2 银行的损失分布、资本配置与存款保险定价

2.1 损失分布、资本配置与存款保险定价

给定银行的损失分布,银行的资本配置和存款保险定价的关系可以用图1来说明。在存款保险制度下,银行的损失实际上是由股东和存款保险机构共同承担的。损失准备金、风险资本和存款保险构成了银行风险管理的三道防线。如果银行的损失超过风险资本和损失准备金之和,那么它的全部资本就将被耗尽,银行将被迫实行破产清算,超额部分的损失将由存款保险机构来补偿。

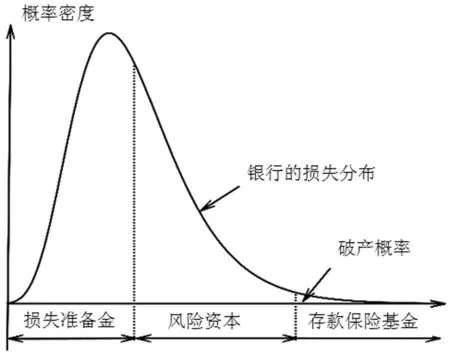
图1 单位资产损失的概率密度

2.2 存款保险机构的损失赔付函数

在讨论存款保险基金的赔付函数之前,本文做如下基本假定:第一,存款保险费为事前支付。第二,存款保险基金的来源是参保银行缴纳的保费。第三,沿用MERTON模型的“银行的负债全部为存款且全部被保险”的假定。简单起见,本文不考虑监管宽容。假定银行的损失用随机变量L表示,其概率分布函数为F(L)。当银行的损失超过损失准备金和风险资本之和时,存款保险机构将履行赔付责任,预期的赔付EL可表示成:

(1)

式(1)中,LR,RC分别代表银行计提的损失准备金和风险资本。假定缴费时刻银行全部负债为存款D,资产为A,则单位存款的预期损失g可表示成:

(2)

定义η=D/A,由于假定银行全部负债为存款,η则为银行的资产负债率。故g可表示为:

(3)

公式(3)右侧的第2个带有积分的分式项,实际上表示的是单位资产的损失。若将银行全部资产看成是贷款的话,公式(3)本质上是将银行资产的损失转换成单位存款的损失来定价存款保险,这与LAEVEN的方法是一致的,只不过相较而言对银行资产的损失测算更精确。根据《存款保险条例》规定,存款保险基金一般投资于政府债券等低风险金融资产,因此可近似认为它的收益率为无风险利率rf。从维持存款保险基金平衡的角度看,期初银行缴纳的保费应能恰好弥补期末的预期损失。于是期初的保费应为:

(4)

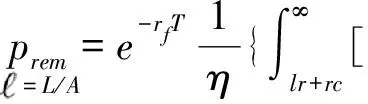
(5)

3 单位资产损失分布的测算

测算银行单位资产损失分布的思路是:第一,对银行的资产进行抽样。考虑到统计学中已有成熟的抽样方法,本文不拟对抽样方法加以讨论。第二,测算资产组合的损失分布。第三,将资产组合的损失除以抽样时该组合的资产总额,便得到单位资产的损失分布。

严格地说,银行资产的构成具有一定的多样性。但考虑到银行的损失主要是信贷资产的损失,本文后继对银行单位资产损失分布的讨论将基于信贷资产组合来展开。

3.1 测算银行单位资产损失分布基本原理

3.1.1 测算抽样的资产组合损失分布

假定抽样获得的贷款组合中未来1年会有Nd笔贷款违约,每笔违约贷款损失为Xi,i∈{1,2,…,Nd}。显然,Nd和Xi都是随机的。于是,违约贷款损失之和Ls的矩母函数为:

MLs(t)=E[et(Ls)]=ENd[E[et(X1+X2+…+XNd)|Nd]]

(6)

若将每笔违约贷款的损失Xi看成是服从同一分布且彼此独立,则公式(6)可表示为:

MLs(t)=ENd[MX(t)Nd]=PNd[MX(t)Nd]

(7)

其中,MX(t)为单笔贷款的损失矩母函数;PNd[]为违约数目Nd的概率生成函数。公式(6)表明贷款组合损失的矩母函数MLs(t)可以看成是由PNd[]和MX(t)两者复合而成。所以,需要依据抽样数据给出PNd[]和MX(t)的具体函数形式。现假定贷款组合总的损失Ls的矩母函数MLs(t)是已知的,根据GORDY[10]的研究,已知损失的矩母函数,利用鞍点法测算违约贷款组合损失分布的尾部具有较好的特性,这恰好能满足存款保险定价对测算精度要求。

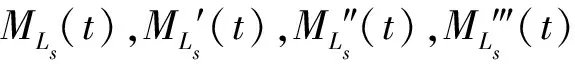
(8)

其中:

(9)

3.1.2 单位资产损失分布的测算

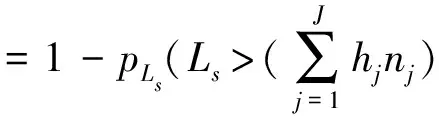
(10)

3.2 测算资产组合损失分布数据形式

为了适应上述测算要求,本文借鉴Creditrisk+模型来测算信贷资产组合的损失。所不同的是本文还需要收集贷款违约损失率的数据,引入违约损失率变量目的是更精确地测算存款保险费率。参考Creditrisk+的作法,需首先将抽样获得的N笔贷款进行分组。将其中额度比较接近的贷款归入一组,不妨假定全部抽样贷款被划分成J组。例如,额度接近1万元的贷款划分到第1组,该组贷款额度近似用h1来表示;接近2万元的贷款放在第2组,其贷款额度用h2表示,等等。不失一般性,假定第j组对应的贷款数目为nj,对应的贷款额度为hj。其次,根据银行不同信用评级贷款的历史违约数据,可测算出该级别贷款违约概率的均值和标准差,具体方法参见张金宝[12]的研究,不再赘述。

3.3 贷款组合中违约贷款数目Nd随机性质

(11)

(12)

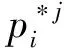
(13)

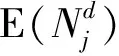
(14)

(15)

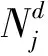
(16)

(17)

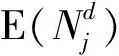
(18)

同理,假定影响所有贷款的共同因素的影响因子Θ服从Gamma(α,β)分布,当给定Θ值时,所有贷款的违约事件相对独立。于是,抽样组合中违约贷款数目Nd的随机性质只取决影响因子Θ的变化,可表示成:

(19)

(20)

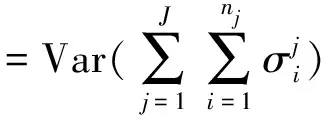
(21)

同理,沿用公式(18)估计参数的做法,同样可以估计参数α,βμ*:

(22)

3.4 单笔贷款的违约条件损失X的随机性质

现在考虑违约贷款的损失X的概率分布。显然,X由违约贷款的额度H和违约损失率Ξ共同决定,即:

X=H×Ξ

(23)

对于获得的抽样而言,未来1年里究竟抽样中哪笔贷款违约,违约后的损失率大小如何均具有随机性。从这个意义上,违约贷款额度H和违约损失率Ξ均看成是随机变量。

3.4.1 违约贷款额度H的概率分布

根据抽样的分组数据,违约贷款额度H的概率分布可用离散的概率分布表示:

(24)

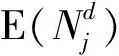
3.4.2 违约贷款损失率的分布

关于违约贷款的损失率,其影响因素比较复杂。现有文献在论及其统计特征时多用beta分布来描述[13],概率密度函数可表示为fΞ(ξ|a,b),其中a和b是beta分布的参数。本文采用beta分布描述违约贷款损失率Ξ。

3.4.3 违约贷款损失X的分布

求解违约贷款损失X的分布,实际上是求解违约贷款额度H和违约损失率Ξ两个随机变量乘积的分布。最近的研究认为贷款额度与违约损失率并没有显著的关系[14],为此可将贷款额度H和违约损失的概率Ξ看成是彼此独立的。于是,根据刘继成和胡晓山[15]的研究,单笔贷款损失X的概率密度函数可以表示成:

(25)

公式(25)引入为违约损失率变量,主要是考虑到存款保险机构通常是在对银行破产清算之后,再赔付存款人的损失。贷款违约损失率的高低,会对银行资产清算后的价值有重要影响。因此引入该变量会大大提高存款保险费率的测算精度。

3.5 贷款组合损失的矩母函数的具体形式

当把全部贷款的违约概率看成受一个服从Gamma(α,β)分布的随机因子Θ影响时(即μ=Θμ*),根据公式(19),违约数目Nd的概率生成函数PNd(t)为:

PNd(t)=E[E(PNd(t))|Θ]

(26)

(27)

对公式(26)(27)进行复合运算(参见公式(7)),即得到了抽样贷款组合损失LS的矩母函数,然后运用鞍点法进行求解,代入到公式(8)中,就可以求解抽样贷款组合损失LS的概率分布,进而计算单位资产的损失分布,再运用公式(5)即可定价存款保险。

4 一个具体的算例

本节以某沿海城市A银行为例,提供一个具体的算例。抽样时间为2016年8月底,抽样时采用不放回的简单随机抽样方式,共获得贷款332笔。

4.1 关于数据

4.1.1 贷款抽样数据及其初步处理

第一,对抽样贷款进行分组。本文以20万元为单位对332笔贷款进行分组。具体地,小于或等于20万元以下的贷款划分为第1组,小于或等于40万元的贷款划分为第2组,因有的区间没有贷款,所以共计划分77组(即J=77)。考虑到在计算单位资产损失时,需要用贷款损失除以所有贷款额度的总和,为不致引起误差,本文用每组贷款额度的平均值作为该组贷款的额度hj,并统计每组贷款的个数nj。

表1 不同信用级别贷款的违约概率的均值和标准差(单位:10-4)

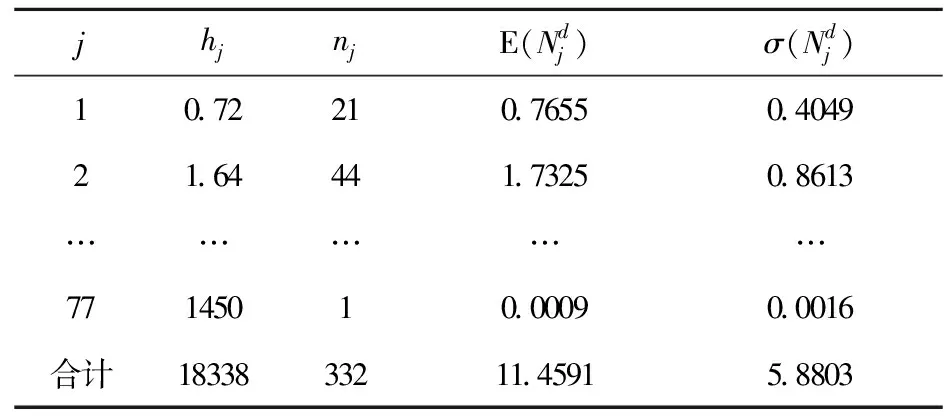
表2 贷款抽样数据分组情况

第三步,选取恰当的违约损失率的参数。本文参考该银行所属地区的贷款违约后回收率的情况,收集贷款损失后的回收数据共计439个数据,测算出其均值为40.36%,标准差为7.76%。然后用所得到的回收数据估计了beta分布的参数:a=0.8313,b=1.1892。

4.1.2 其他变量

根据公式(5)的要求,本文收集了该行2016年资产负债、银行资本方面的数据,这些数据均来自银行公开披露的数据,据此本文算出存款保险定价所需的参数值,详见表3。无风险利率rf选用当年1年期国债的平均利率2.18%。

表3 存款保险定价算例的其它参数

4.2 对存款保险定价的分析与测算

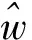
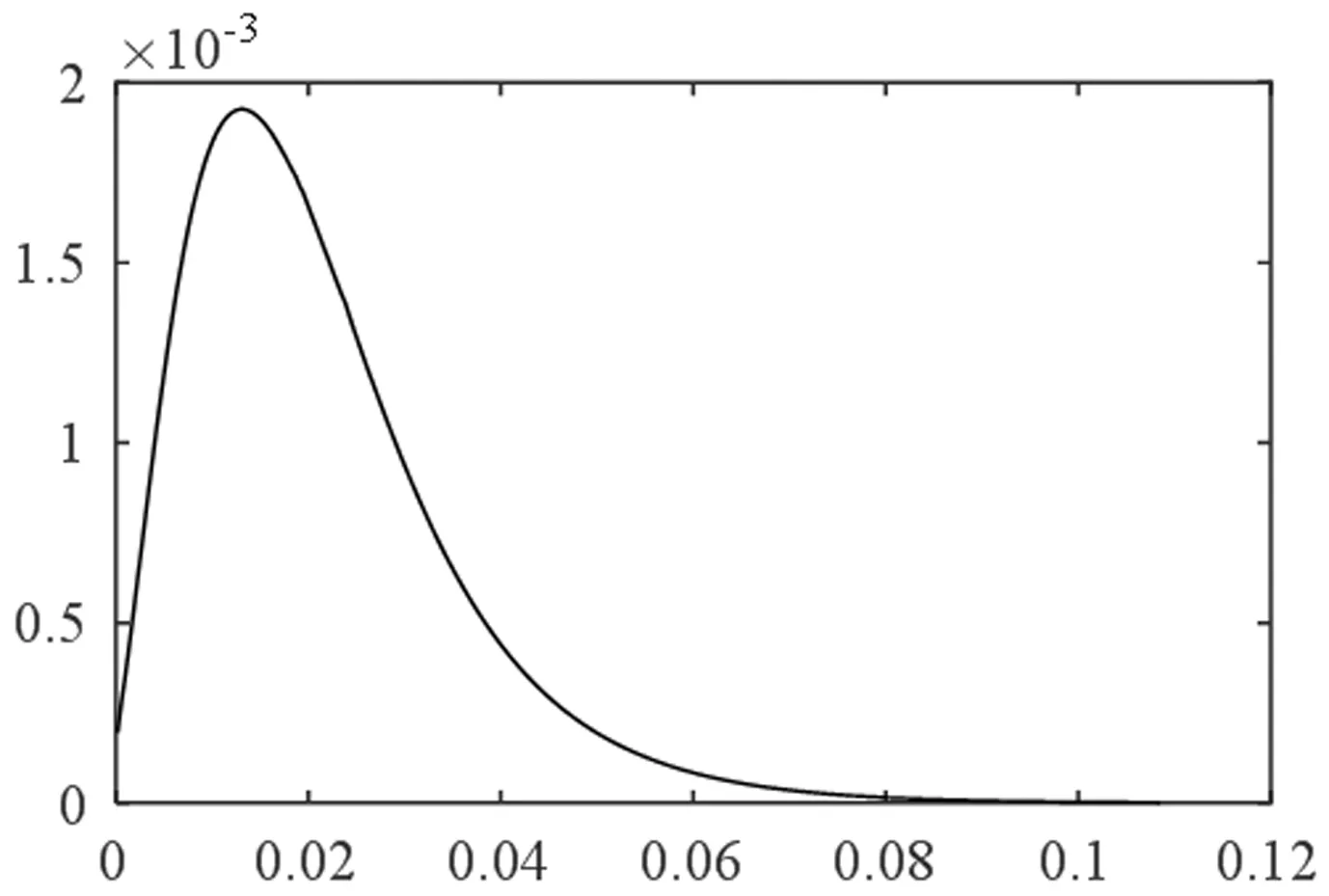
图2 单位资产损失的概率密度

4.3 关键因素对存款保险定价的影响

借助本节的算例,可以直观地考察贷款违约损失率对存款保险费率的影响。由于假定违约损失率呈beta分布,简单起见本文保持beta分布的方差不变,改变分布的均值,来分析违约损失率对存款保险费率的影响。从图3可以看出,当违约损失率均值由35%上升至55%时,存款保险费率由0.6个基点上升至11.5个基点,增加近20倍。这表明,存款保险费率对商业银行贷款的违约损失率变动比较敏感,说明引入贷款违约损失率变量是非常必要的。显然,有效降低存款保险费率,应更加关注违约损失率的影响。

图3 违约损失率与存款保险费率

5 结论

本文的方法使存款保险定价所面临的困境得到解决,它具有如下特点:

第一,提出了基于银行单位资产损失分布的存款保险定价新方法。该方法将信用风险研究成果引入到存款保险定价的领域,拓宽存款保险定价的研究思路。

第二,提出了利用抽样数据估算银行单位资产损失分布的具体方法,节省了估算银行资产损失的成本。此外该方法将违约损失率引入到损失分布的概率模型中,克服了Creditrisk+模型的缺点,从而有效提高模型的测算精度。

第三,该方法不依赖于外部评级数据和银行股票的市场价格数据,适用范围不再受到限制,具有广阔的应用前景。所采用的数据具有良好的可获得性。其中银行的资产、负债以及风险资本等基础数据均是公开披露的数据。国家金融监督管理总局通常会要求商业银行提供贷款组合的风险模拟和测算情况,因此贷款组合的抽样数据可以从监管数据中获得。当然,这需要存款保险机构未来能够和监管机构实现数据共享,在制度层面是可以解决的。