马尔可夫决策过程在类风湿关节炎治疗中的应用研究

徐伟锋, 曹 平

(中国科学技术大学 管理学院,安徽 合肥 230026)

0 引言

类风湿关节炎(RA)是一种常见的慢性自身免疫性疾病,发病人数约占全球总人口的0.24%[1]。其通常伴随着心血管疾病、呼吸系统疾病、胃肠道疾病、神经系统疾病、血液系统疾病和肾脏疾病等合并症,还可能使患者出现焦虑、抑郁和睡眠障碍等精神问题,极大地增加了患者死亡的风险[2]。在我国,RA的发病率为0.42%,患者人均门诊用药费用为8018元,这给普通劳动人民患者带来了一定的经济压力[3]。因此,更快地制定合适的治疗方案尤为重要。

近年来学者们从不同的角度对RA展开了较多的相关研究。一方面,学者们关注于通过临床试验来得到更优的治疗方案[4,5],然而这些试验往往需要花费较大的人力物力,并且由于患者的健康状况并不是完全暴露的,医生往往需要在一个不确定的环境中进行多阶段决策,同一种治疗策略可能对不同患者的效果是随机的,因此疗效具有很大的不确定性。另一方面,学者们致力于使用数据挖掘的方法从RA患者的电子病历中寻找患者的用药规律以及药物对疗效的影响,例如陈梦娜等[6]使用关联规则、聚类分析等方法对RA患者的用药规律进行了挖掘,XIE等[7]使用关联规则探究了RA患者一些实验室指标与中药之间的关系,但是他们都是从医疗数据挖掘的角度寻找进行了研究,并没有涉及医疗决策问题。本文使用的马尔可夫决策过程(MDP)能够较好地在不确定环境中对RA患者的住院流程进行建模,并且能从患者决策的角度给出相应的治疗策略。

我们的工作还与MDP模型在医疗保健决策领域的应用相关。在医疗保健决策领域中,MDP模型有着广泛的应用,例如ALAGOZ等[8]建立了一个用于确定最佳肝移植时间的MDP模型,CHHATWAL等[9]根据女性乳房X光片特征和人口统计学信息基于有限阶段准则建立了一个MDP模型以确定进行乳腺活检的时间,BAZRAFSHAN和LOTFI[10]基于有限阶段准则建立了一个MDP模型,其可以根据癌症患者的病情选择最优的化疗方案。但是以上研究都是基于有限阶段准则进行建模,并未将RA这类需要终身治疗的慢性疾病考虑进去。本文从RA患者的电子病历中提取数据,基于无限平均准则将MDP模型应用于这些患者的治疗过程中,并且详细给出了MDP模型五元组的构建过程,最后得出了最优治疗策略以及治疗报酬和成本。

基于上述研究,本文创新地在无限平均准则下将MDP模型应用于RA患者的治疗过程中,主要贡献如下:首先,本文利用RA患者电子病历中的数据建立了一个MDP模型,该建模流程不仅可以应用于RA的治疗过程中,还可以适用于其他慢性疾病的治疗中;其次,我们发现本文所建立的MDP模型得到的治疗报酬与治疗成本均优于医院现有治疗方案下的治疗报酬与治疗成本,这就显示了MDP模型在RA治疗中的潜力与价值,它在降低RA患者的治疗成本的同时,提高了医院的治疗效率。

本文的内容安排如下:第0节为引言,第1节给出研究样本与数据来源;第2节给出模型构建的整个过程;第3节给出最优策略的求解方法;第4节给出模型相应的结果以及稳健性检验;第5节给出本文的结论。

1 研究样本与数据来源

本研究所使用的资料来自安徽中医药大学附属第一医院风湿科患者的电子病历。这些患者于2012年6月至2016年6月期间在该院住院治疗。电子病历包括患者的基本信息、就诊信息、实验室指标信息以及用药信息等。我们从中选取了被诊断为RA患者的电子病历,并进行了如下样本筛选:(1)排除住院期间未使用中药进行治疗的患者;(2)排除被诊断为有严重并发症的患者和怀孕患者;(3)排除住院期间只进行检测了一次实验室指标检查的患者。最终共得到858例RA患者的电子病历数据,其中女性741例(86.36%),男性117例(13.64%)。患者的平均年龄为53.85岁,平均住院天数为16.69天。

2 模型构建

住院患者的具体流程如图1所示:

图1 患者住院治疗流程图

由图1可知,患者在t0时刻入院后,其在t1时刻会去检查症状与实验室指标,在t2时刻医生会根据患者的身体状况做出诊断并给出相应的治疗方案,在t3时刻患者开始接受治疗,之后患者可能会继续接受几次症状与实验室指标检查,然后医生继续给出治疗方案直至其符合出院标准出院。在此过程中,患者的症状与实验室指标检查并不能完全代表患者真实的身体状况,医生往往是在不确定的环境下做出多个阶段的医疗决策,该过程正好适合用MDP模型来进行建模。MDP模型由五元组构成,其分别为决策时刻、状态、行动、转移概率函数和报酬或成本,可参见刘克和曹平[11]第1章第3节。下面我们将在每一小节中给出这些要素的定义方式。

2.1 决策时刻

患者经过实验室指标检查后,医生会根据其健康状况给出相应的治疗方案。把医生每次给出治疗方案的时间点记为决策时刻,用T记所有决策时刻的点集。

2.2 状态

患者真实的健康状况是隐藏的,医生通常通过对患者的症状和实验室指标检查来推测患者的身体状况。本研究中,我们根据医师的建议和相关文献,从患者的实验室指标中选择了9个关键指标来近似患者的身体状况,这些指标通常用于评估治疗效果。这些指标可分为三类,分别是炎症指标(CRP,ESR,RF)、肝功能指标(ALT,AST)和血液学指标(RBC,HGB,PLT,WBC)。CRP,ESR和RF作为RA的诊断标准[12],它们能帮助了解体内的炎症水平。ALT和AST能帮助医生了解患者用药过程中肝功能是否有损伤。检查RBC和HGB能监测贫血,检查PLT能了解是否有血小板增多,检查WBC能了解是否有白细胞减少。而贫血、血小板增多与白细胞减少在RA患者中较为普遍[13]。为了讨论的方便,我们将上述指标的值离散化成两类,处于正常值参考范围记为正常,未处于正常值参考范围记为不正常,并分别用{1,0}表示。

接下来定义状态s。若将状态s定义为s=(I1,I2,…,I9),其中Ii表示上述9个指标的取值,则一共有29种可能,以此进行分析有以下问题。首先是转移概率矩阵会变为稀疏矩阵,对于转移概率的估计会产生较大的偏差,其次是求解会变得更为复杂,最后是按此求得的策略并不具有普适性,不利于现实中的应用。为了减少状态的个数,我们选取患者用药前和用药后检查的上述实验室指标,将其作为特征变量进行聚类分析。而K-modes聚类算法作为一种常用的聚类算法,其常用于对分类属性型数据的聚类中。本研究使用该聚类算法生成每个患者用药前后的状态。每个患者都将根据聚类结果归入一个状态,每一个状态代表患者的健康状况。但是在使用该算法之前,需要指定聚类的数目K。本研究中,首先令K∈{2,3,…,10},然后对于每个K,我们多次使用该算法进行测试,发现当聚类数等于6时,分类结果是合理且可以解释的。这些患者刚好可以根据有多少个炎症指标异常、贫血指标是否异常、血小板是否异常、白细胞是否异常以及肝功能是否异常进行分类。该结果与RA实验室指标可能出现的情况刚好一致,聚类结果如表1所示。

表1 K-modes算法聚类结果

由上可知,根据聚类结果可将患者的状态分为6类。当患者处于状态1时,ALT,AST与RF不正常,其他指标正常;处于状态2时,CRP,ESR,RF与HGB不正常,其他指标正常;处于状态3时,CRP,ESR,RF,HGB,RBC,WBC与PLT不正常,其他指标正常;处于状态4时,ESR与RF不正常,其他指标正常;处于状态5时, RF不正常,其他指标正常;处于状态6时,ALT,AST,CRP,ESR与RF不正常,其他指标正常。

2.3 行动

在这些患者的治疗过程中,大约有260种中药被使用,而由于中药处方的种类繁多,因此把每个处方视为不同的治疗方案是不切实际的。于是我们把在第一次和第二次实验室指标检查之间使用的中药作为行动的基础。为了减少行动的个数,我们根据药典将使用的中药分为22个大类,删除使用较少的中药类别,最后得到8大类中药,分别为利水渗湿药、活血化瘀药、补虚药、清热药、祛风湿药、理气药、消食药和祛痰药。我们发现这些患者均使用了利水渗湿药、活血化瘀药、补虚药、清热药、祛风湿药和理气药,不同之处在于是否使用了消食药和祛痰药,其中未使用消食药和祛痰药的有349人,使用消食药的有164人,使用祛痰药的有191人,而既使用了消食药也使用了祛痰药的有154人。为了研究消食药和祛痰药对患者的影响,我们定义如下行动空间,对于任意的i∈S,A(i)={a1,a2,a3,a4},其中a1表示未使用消食药和祛痰药,a2表示使用消食药,a3表示使用祛痰药,a4表示使用消食药和祛痰药,即医生在患者处于任何状态i(i∈S)时可从行动a1,a2,a3与a4中选取其中一个。

2.4 转移概率函数

函数p(s′|s,a)称为转移概率函数,其表示当前决策时刻状态为s,若采取行动a,到下一个决策时刻转移到s′的概率。由前面定义的状态与行动可知,患者的状态有6个,即状态1到状态6,我们分别将其记为s1,s2,s3,s4,s5与s6,采取的行动有4个,即a1,a2,a3与a4。比如说,我们想计算处于状态2的患者在使用消食药后变为状态1的概率,那就是要计算p(s1|s2,a2)。我们可以先统计数据中所有这类患者的数量,得到n(s1|s2,a2)。然后,我们再统计数据中所有处于状态2并使用消食药的患者数量,得到n(a2|s2)。我们用这两者的比率来近似p(s1|s2,a2)。在我们的数据中,n(s1|s2,a2)=23,n(a2|s2)=61。因此,我们用23/61来近似p(s1|s2,a2)。对于处于其他状态,采取其他行动的转移概率,也可由同样方式求得。

2.5 报酬与成本

医生根据患者的状态会采取不同的行动,该行动可能是确定性的,也可能是随机的。本研究中,由于患者的健康状况并不是完全暴露的,且根据我们的数据,医生对于处于相同状态下的患者会随机地选取行动,因此医院的策略是随机的。医院的随机策略定义为π:S×A→[0,1],此时π(s,ai)=P(ai|s)。医院的具体策略如表2所示。

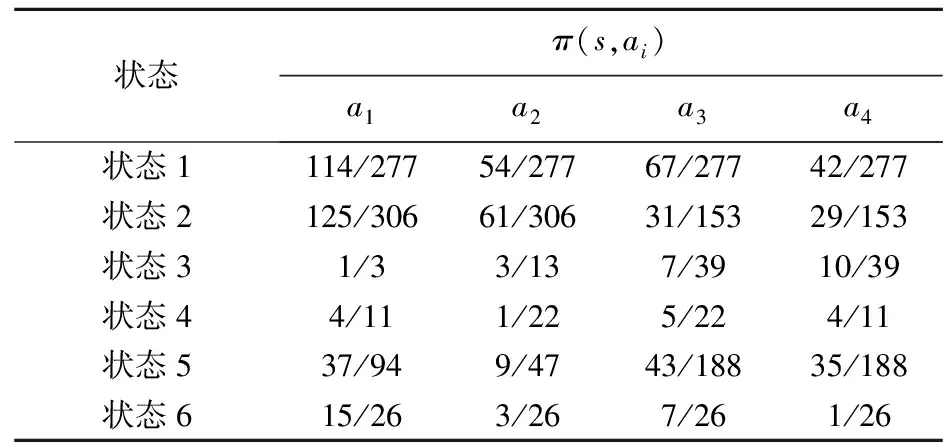
表2 医院策略

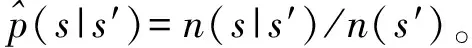
于是可将指标R定义为

(1)

其表示医院在上述策略下的平均报酬,其值记为r。

然后我们介绍第二个度量指标C,我们将患者两次实验室指标检查已住院的天数视为成本,住院天数越长,患者所需支付的医疗费用越多,成本就越大。患者从状态s转移到状态s′已住院的平均天数记为δ(s,s′),成本C(s,a)表示患者在处于状态s时采取行动a所需付出的成本,其计算公式为

于是可将指标C定义为

(2)

其表示医院在上述策略下的平均成本,其值记为c。

3 最优治疗策略的求解方法

在无限阶段平均准则下,当MDP为单链且状态空间与行动空间均有限时,必定存在一个最优的确定性策略[11]。由于本文考虑两个度量指标,因此一一给出这两个度量指标下最优治疗策略的求解方法。

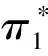
(3)

(4)

(5)

(6)

(1)取V0=0,取定迭代精度ε>0,k=0。

(2)对于每个i∈S,利用

(7)

得到Vk+1。

(4)此时对每个i∈S,取

(8)

然后停止。

4 结果分析

4.1 模型结果

通过上述的求解方法,可得最优策略和报酬与成本,如表3和表4所示。

表3 最优策略

表4 报酬与成本

4.2 稳健性检验

表5 新行动空间下的最优策略

表6 新行动空间下的报酬与成本

5 结论

本文基于无限阶段平均准则将MDP模型应用于RA患者的中药治疗过程中。首先我们从已有的数据中推断出建立MDP模型所需的各个参数,然后我们使用相对值迭代算法来求解这一问题并得到了相应的治疗策略。结果表明,本文建立的模型得到的治疗成本要低于医院的治疗成本,报酬要高于医院的报酬,这对RA的临床治疗具有一定的指导意义。本研究仍然存在一些局限性,首先我们没有考虑其他治疗方法,如熏蒸、推拿、针灸和西药等,未来可把这些纳入模型的行动中;其次患者的健康状况是隐藏的,并没有完全暴露,部分可观察的马尔可夫决策过程可能是一个很好的模型,今后研究可以从这方面开展。