基于预防维修的可变抽样区间泊松EWMA控制图经济设计

薛 丽, 曹逗逗, 王秋语

(郑州航空工业管理学院 管理工程学院,河南 郑州 450046)

0 引言

随着现代高新企业智能制造技术的广泛运用以及大量过程数据获取的便捷性,产品制造过程监控日益受到关注。由于人、机、料、法、环、测的影响,产品相关的质量特性值将会偏离目标值,即过程波动经常存在。统计过程控制是应用统计技术对过程各个阶段进行评估和提升质量的一种有效技术和方法,通过其重要的工具——控制图对过程进行监控可以快速识别异常波动,达到提高过程质量的目的。为了监控产品缺陷数的异常波动,休哈特提出泊松分布下缺陷数c控制图,由于仅仅考虑现时样本点的影响,只有当过程中的波动达到一定程度大时其监控效果才比较明显。1959年ROBERTS[1]基于指数加权形式放大单个样本点的信息,提出对过程中较小波动监控灵敏的EWMA控制图。

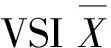
为了降低过程控制成本,DUNCAN[9]提出了控制图的经济模型,以确定均值控制图的参数最优值。FRANCO等[10]用变采样策略监测自相关数据,构建了休哈特控制图的经济模型。NADERKHANI和MAKIS[11]研究了具有两个采样区间的多元贝叶斯控制图的经济设计。COSTA和FICHERA[12]运用一种改进的自适应差分进化方法,研究了ARMA控制图的经济统计设计。CHOU等[13]对VSI EWMA控制图经济设计进行研究。SEIF等[14]提出一种运用马尔可夫链方法对VSST2控制图进行经济设计研究。王海宇等[15]基于平均产品长度,构建EWMA控制图的多目标经济统计优化模型。薛丽[16,17]针对标准差变化和产品缺陷数变化的两种情形,研究抽样区间变化的EWMA控制图的经济设计问题。

随着生产过程机器化和自动化的日益普及,产品制造流程也从人工时代向机器化时代转变。此时,设备运行状态是否正常越来越重要,密切影响到产品的质量、过程控制的效果以及控制成本。学界和业界均认为设备运行状况与过程质量存在密切联系,许多学者持续关注设备维修管理与过程质量控制的联合决策研究[18-21]。另一方面,由于高精度产品测量成本日益增高,强调产品质量输出偏离目标值的质量损失函数被广泛使用在制造过程中。传统的经济模型关注过程控制成本,较少考虑偏离目标值造成的质量损失[9-17]。因此,本文基于质量损失函数和预防性维修策略,研究可变抽样区间泊松EWMA控制图的经济设计问题,构建其经济模型。对其进行灵敏度分析,以指导在实际生产过程中如何选择最优的控制图参数。

1 可变抽样区间泊松EWMA控制图

令X为生产过程中单个产品中的缺陷数,一般情况下服从泊松分布:

P{X=x}=e-μμx/x!,x=0,1,2,…

(1)

其中,μ>0为已知参数。过程受控时,μ=μ0。过程失控时,μ=μ1=μ0+μ0δ,δ为均值波动。则容量为n的样本中包含的总缺陷数表示为Y=X1+X2+…+Xn,它服从参数为nμ的泊松分布:

P{Y=y}=e-nμ(nμ)y/y!,y=0,1,2,…

(2)

则受控状态下Y的均值和方差为:

(3)

泊松EWMA控制图的监控统计量Z0为:

(4)

根据式(3)、式(4)可以得出:

(5)

当t充分大时,得到Zt方差的渐近形式:

Var(Zt)≈λnμ0/(2-λ),0<λ≤1

(6)

其中,λ为平滑系数。泊松EWMA控制图的上下控制限为:

(7)

(8)

其中k1,k2为上下控制限系数。

由于式(4)得到的统计量Zt≥0,当LCL≤0时,控制图检测不出均值的向下波动,此时的控制图应该为非对称的,因此取k1≠k2。

泊松EWMA控制图的上下警戒限为:

(9)

(10)

其中w1,w2(0

选取h1和h2为两抽样区间,且h1>h2>0,若LWL≤Zt≤UWL,则间隔h1抽取下一个样本;若UWLUCL或Zt

2 经济模型建立

为了建立经济模型,有如下假设:

(1)过程最初为受控,即μ=μ0;

(2)总缺陷数服从参数为nμ的泊松分布;

(3)若过程失控时,总缺陷数nμ=nμ1=nμ0+δnμ0;

(4)受控时间服从参数为θ的指数分布;

(5)异常原因不发生在抽样时,且最多有一个[10];

(6)一旦过程发生波动,不可能自动恢复到受控;

(7)当UWL

2.1 过程循环周期T的确定

将从开始到失控,寻找并消除异常原因的时间称为过程循环周期T。T可以分为:(1)受控时间;(2)失控到报警的时间;(3)分析样本并记录的时间;(4)异常原因找到以及过程纠正的时间。表1记录经济模型的有关参数,T的公式如下:

表1 相关参数定义

T=1/θ+(1-γ1)st0/ANSS0+ATS1-τ+t1+t2+ng

(11)

2.2 损失成本函数L的确定

一个循环周期的损失成本有:(1)错误警报、作图和异常原因找到并纠正的损失成本L1;(2)预防维修损失成本L2;(3)受控损失成本L3;(4)失控损失成本L4。

(1)错误警报、作图和异常原因找到并纠正的损失成本L1为:

L1=α×(1/θ+(1-γ1)st0/ANSS0)/h0×d+

(12)

(2)预防维修损失成本L2为:

L2=Cpm×[p01×(1/θ+(1-γ1)st0/ANSS0)/h0+

(13)

其中p01为受控时落在警戒域的概率,p11为失控时落在警戒域的概率。

(3)记m为目标质量特性值,Δ为容差,M/Δ2为损失函数系数。受控时,将均值和目标值的绝对偏差记为dv,即dv=|μ-m|,则受控时期损失成本L3可表示为:

(14)

其中y为单位内的产品生产量。

(4)当异常原因发生时,损失成本L4可表示为:

(ATS1-τ+t1+t2+ng)y

(15)

因此得到损失成本函数L为:

L=L1+L2+L3+L4

(16)

2.3 单位时间的损失成本函数ETL

由式(11)和式(16)得到单位时间的损失成本函数ETL:

ETL=L/T

(17)

由前面讨论可知ETL是与参数(n,k1,k2,h1,h2,w1,w2,λ)有关的函数。

3 数据案例

下面通过给出航空玻璃纤维布的例子说明求解参数(n,h1,h2,k1,k2,w1,w2,λ)最优解的过程。

为了提高过程质量,某航空制造企业采用VSI泊松EWMA控制图对玻璃纤维布上的瑕疵点监控。受控时,服从参数为μ=μ0=4的泊松分布,失控μ=μ1=μ0+δμ0=6时。模型和成本相关参数如下:a=1.5,b=0.5,Δ=4,W=4,d=2,m=4,g=0.2hr,t1=0.6hr,t2=0.6hr,θ=0.01,γ1=γ2=1,y=12,Cpm=10,M=10。

matlab环境下对遗传算法进行编码。要求n为整数,参数(n,h1,h2,k1,k2,w1,w2,λ)的取值范围为:1≤n≤20,1≤h1≤3,0.01≤h2≤1,1≤k1≤4,1≤k2≤4,0.01≤w1≤3,0.01≤w2≤3,w1≤k1,w2≤k2,0.01≤λ≤1。人口规模N为30,变异率和交叉率为0.1和0.8,令ETL(式(17))的倒数为适应度函数。当迭代到100代时算法停止,得到VSI泊松EWMA控制图的最优值参数:n=2,k1=3.518,k2=1.979,h1=2.758,h2=0.121,w1=1.73,w2=1.933,λ=0.062,ETL=262.1259。

4 灵敏度分析

为了研究(a,b,θ,d,g,t1,t2,δ,Cpm,W,M)与(n,h1,h2,k1,k2,w1,w2,λ)和ETL间的关系,对经济模型进行参数灵敏度分析。(a,b,θ,d,g,t1,t2,δ,Cpm,W,M)为自变量,对应的水平记在表2,(n,h1,h2,k1,k2,w1,w2,λ)和ETL为因变量。这是两水平十一因素的正交试验,可以选用正交表L16(215)。令γ1=γ2=1,t0=1。由L16(215)得到的试验方案以及结果记在表3和表4。

表2 十一个模型参数的两种水平

表3 根据L16(215)安排的十六次试验

令显著性水平α=0.1,运用SPSS软件对因变量进行回归分析,得到参数之间的影响关系,具体见表5。

表5 设计参数或ETL与模型参数间的影响关系

5 最优性分析

某一产品缺陷数服从泊松分布,受控时参数μ=μ0=4,失控时μ发生波动,可以采用VSI泊松EWMA控制图监控。下面对基于经济方法设计和统计方法设计的两种控制图做比较研究。

(1)样本容量n=2时,由统计方法设计VSI泊松EWMA控制图。令受控ATS0为固定值,使失控ATS1达到最小得到(n,h1,h2,k1,k2,w1,w2,λ)的最优值。

(2)基于经济方法构建的VSI泊松EWMA控制图。根据所建立的经济模型(17)得到(n,h1,h2,k1,k2,w1,w2,λ)的最优值。

在表2给定参数值的前提下,计算单位时间损失成本并进行比较。根据统计方法得到的单位时间损失成本记为ETL1;根据经济方法得到的单位时间损失成本记为ETL,相关结果记录在表4。令n=2,k1=2,k2=3,w1=1,w2=2,分别计算λ=0.05,ATS0=250,300,350和λ=0.1,ATS0=150,200,250时,16次试验得到的单位时间损失成本,并记在表6。

表6 最优性分析结果

由表6可知:每种试验下基于经济方法设计得到的单位时间损失成本ETL均小于统计方法设计得到的单位时间损失成本ETL1,因此基于经济方法设计的控制图优于统计方法设计的控制图。

计算16次试验得到的单位时间损失成本平均值,并记录在表中倒数第二行。例如,基于经济方法设计得到的单位时间损失成本ETL均值为230.367,而当λ=0.05,ATS=300,时,用统计方法设计得到的单位时间损失成本ETL1的均值为256.244,得到ETL

最后平均值除以ETL均值230.367,得到标准化之后的比值并记在最后一行。例如:λ=0.1,ATS=200时标准化比值为1.1106,说明基于经济方法设计的控制图ETL优于统计方法设计的控制图1.1106倍。

综上可知:基于经济方法设计的VSI泊松EWMA控制图优于统计方法设计的控制图。

6 结论

本文引入预防维修策略,构建基于二项分布的VSI泊松EWMA控制图经济模型;采用遗传算法令目标函数最小化得到经济模型的最优解;然后对经济模型进行灵敏度分析,得出参数(a,b,θ,d,g,t1,t2,δ,Cpm,W,M)与(n,h1,h2,k1,k2,w1,w2,λ)间的关系,为实际中选取最优参数提供参考建议,建议分别为:(1)过程均值波动δ增大时,建议降低控制图的样本容量n,增大上控制限系数k1、上警戒限系数w1、平滑系数λ;(2)异常原因发生的频率θ增大时,建议降低上控制限系数k1、下控制限系数k2、上警戒限系数w1和下警戒限系数w2;(3)发现及修复一次异常原因的平均成本W增大时,建议增大上控制限系数k1,减小下控制限系数k2;(4)发现过程异常原因的时间t1增大时,建议增大上控制限系数k1,减小上警戒限系数w1;(5)纠正过程的平均时间t2增大时,建议增大上控制限系数k1;(6)抽取一个样品并记录它的时间g变大时,建议调大上控制限系数k1,上警戒限系数w1;(7)在使用控制图对过程进行监控时,如果统计量落在警戒域内,应即时进行预防维修;如果样本点超出了控制限,应立即查找异常原因,采取相应措施纠正过程,以减少不合格品的产生。

通过最优性分析可知:基于经济方法设计的控制图比统计方法设计的控制图单位时间损失成本更小,其经济性能更优越。