毕达哥拉斯三角模糊数密度算子及其应用

易平涛, 王胜男, 李伟伟, 王 露

(东北大学 工商管理学院,辽宁 沈阳 110167)

0 引言

多属性决策[1]是多指标环境下多方案的选择方法,在经济管理、政治、军事、工业,乃至医药卫生等诸多领域广为应用。近年来,受决策问题频度、广度需求日增及现代信息技术迅猛发展的内外驱动,相较于经典处理方式,新时期的多属性决策问题呈现出复杂化、多样化等信息特征。其中,考虑到决策过程中的不确定性、敏感性及决策者偏好等原因,以模糊信息形式为基础的决策问题成为众多学者关注的焦点。

考虑到隶属度与非隶属度之和大于1的情形,YAGER和ABBASOV[2]在直觉模糊集的基础上进一步拓展,提出毕达哥拉斯模糊集(PFS),满足条件为隶属度与非隶属度的平方和小于等于1,从而更清晰地刻画出决策的不确定性本质并确保属性信息呈现的真实性。近年来,基于PFS的拓展性研究逐渐被重视。2019年,何霞等[3]提出PTFN及其集成算子,既有效地解决方案属性值为直觉三角模糊数时可能存在隶属度与非隶属度之和大于等于1的情况,又进一步拓展了PFS的研究领域。PTFN是模糊数据的深度拓展,兼顾毕达哥拉斯模糊集与直觉三角模糊集的优势,为复杂不确定决策情景提供一种新的量化形式。(1)但目前PTFN在决策领域的应用极少,且在PTFN集结过程中没有考虑数据的分布特征,较难适应更复杂的决策环境。

在信息集结过程中,常借助于数据的疏密程度对数据进行聚类,进而刻画数据间的分布结构特征。基于此,易平涛等[4]考虑属性信息分布的疏密关系,构造出密度中间(DM)算子,从而实现数据在信息结构上的二次柔性集结。近年来对于DM算子的拓展研究逐渐深入[5-7]。DM算子充分考虑属性信息分布的疏密,有效增强信息集结过程的准确性。(2)但目前DM算子的研究大多聚焦于普通的评价环境,依托的数据类型多为精确值、语言信息或基础的模糊数[8-12],未有研究运用DM算子解决毕达哥拉斯三角模糊决策问题。

基于以上两点局限性,本文对属性信息为PTFN的多属性决策问题进行探索,考虑数据信息分布的疏密关系,构建出一种新的PTF-DM算子,并参考了CABLES等[13]研究中模糊参考理想法(FRIM)的基本思想以及得分函数实现数据的有效聚类和最终排序。PTF-DM算子是在信息表达及信息集成方向上的有效拓展,既实现多属性决策中模糊数据类型的深度细化,又考虑数据信息分布的不均匀问题,能够有效应对多属性决策问题中逐渐模糊化及复杂化的决策环境。

1 相关概念介绍

(1)

记非隶属函数为v(x):X→[0,1],有

(2)

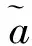
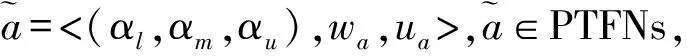
(3)

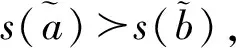
2 毕达哥拉斯三角模糊数的聚类

2016年,学者CABLES等[14]首次提出参考理想法(Reference Ideal Method,RIM),随后,一些学者开展相关拓展研究。2018年,CABLES等[13]将RIM拓展到模糊领域,提出模糊参考理想法(Fuzzy Reference Ideal Method,FRIM),并将FRIM法应用到以PFN为属性信息的决策问题中。2020年,SANCHEZ-LOZANO和RODRIGUEZ[15]将FRIM法应用到属性值为三角模糊数(TFN)的军用训练机优选中,为该研究领域提供新的决策方法。由于PTFN是TFN的推广并符合PFN的性质,因此,基于FRIM法的部分思想实现PTFN的聚类。根据CABLES等[13]、SANCHEZ-LOZANO和RODRIGUEZ[15]的研究,现给出毕达哥拉斯三角模糊数的距离与估值矩阵的相关定义。

(4)

(5)

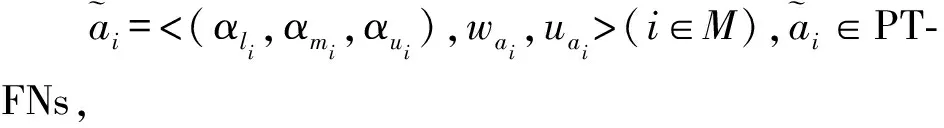
(6)

其中,P,Q,M,N∈PTFNs,IRj=[P,Q]表示参考理想区间,Rj=[M,N]表示取值范围,且满足[P,Q]⊂[M,N]。

归一化的估值矩阵为

针对一维数据聚类问题,CABLES等[14]提出一种聚类方法——有序增量分割法。该法根据数据增量以及间隔的疏密来实现数据的最终聚类。

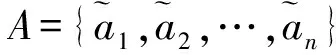
3 毕达哥拉斯三角模糊数密度算子

3.1 基本定义

(7)

(8)

将PTF-DWA算子与PTF-DWGA算子统称作毕达哥拉斯三角模糊数密度算子,记PTF-DM算子,与其他密度算子类似,PTF-DM算子满足幂等性、置换性、有界性、单调性等性质[9]。它可与WA,WAA,OWA,AA,Min,Max等算子结合构建合成算子,下面以WAA算子为例,构建相应的密度合成算子。

定义9设PTF-DWAWAA:Rn→R,称PTF-DWAWAA算子为毕达哥拉斯三角模糊数密度加权平均算子:

(9)

(10)

3.2 密度权重的确定

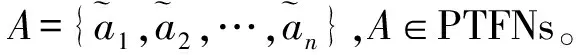
定义10[4]令ξ=(ξ1,ξ2,…,ξm)T为密度加权向量,则有

(11)

密度权重有趋同性、趋极性与趋中性之分,本文依据易平涛等[4]的“组间同性”(Ts(ξ))测度方法与熵值法求解密度权重,规划模型如下:

(12)

4 应用算例

某家风险投资公司需要在6家制造型企业Ci(i=1,2,…,6)中选择一家进行投资,且在进行企业优选时需考虑6个因素,分别为创新能力(f1)、技术基础(f2)、产品质量(f3)、服务品质(f4)、成长背景(f5)、绿色生态(f6)。假设制造型企业Ci(i=1,2,…,6)关于属性fj(j=1,2,…,6)的综合值取值为PTFN,相关决策信息见表1,如<(4.3,6.5,8.4),0.7,0.3>表示制造型企业C1相对于技术基础(f2)方面的得分为6.5,且最大满意度为0.7,而最小不满意度为0.3。假设6家制造型企业中各属性的最高分值是10分,且属性权重向量为w1=(0.1,0.3,0.1,0.2,0.1,0.2)T(计算结果保留三位小数)。

表1 PTFN相关决策信息

下面给出PTF-DM算子的具体计算步骤:

(1)聚类PTFN决策信息

由表1的信息可得出各属性取值范围(R),参考理想区间(IR)可由决策者(即风险投资公司)根据决策需要或属性特点以及取值范围给出,具体结果见表2及表3。

表2 各属性取值范围(R)

表3 各属性参考理想区间(IF)

首先,通过式(3)-式(6)计算出各备选企业各属性的毕达哥拉斯三角模糊数,得到归一化处理后的估值矩阵Y:

根据有序增量分割法,取m=3,实现各备选企业属性的聚类,得到的结果分别为:

企业C1:A1={f2,f3,f6},A2={f1,f4},A3={f5};

企业C2:A1={f2,f3,f6},A2={f5,f4},A3={f1};

企业C3:A1={f2,f3,f6},A2={f1,f4},A3={f5};

企业C4:A1={f1,f4,f6},A2={f3,f5},A3={f2};

企业C5:A1={f1,f4,f5},A2={f2,f6},A3={f3};

企业C6:A1={f1,f2,f4},A2={f5,f6},A3={f3}。

(2)确定密度权重

为体现密度权重(即决策者对信息分布的偏好)对企业最终排序结果的影响,给定“组间同性”测度的不同取值,根据式(12)的规划模型计算出不同取值下的密度权重,详见表4。

表4 不同“组间同性”测度取值下的密度权重

(3)集结决策信息

计算不同“组间同性”测度下的各企业最终评价值并得到最终排序结果,详见表5。同时,图1反映了在不同“组间同性”测度(决策者的信息偏好)下,各企业最终评价值的变化趋势。从表5和图1中可以得出结论:Ts(ξ)取值的不同(即密度权重的不同)会对企业评价值产生影响并最终影响排序结果,这进一步表明考虑决策者信息分布偏好对企业优选具有重要作用。

图1 不同“组间同性”测度下各企业最终评价值的变化

表5 不同“组间同性”测度下各企业最终评价值及排序结果

分别以PTF-DWAWAA,PTF-DWGAWAA,PTF-DWAOWA和PTF-DWGAOWA算子为例,假定决策者偏好群体共识,给出“组间同性”测度Ts(ξ)=0.7,通过PTF-DM算子计算出各企业Ci(i=1,2,…,6)最终评价值和排序结果,如表6所示(PTF-DWAOWA和PTF-DWGAOWA算子中决策信息的位置权重随机生成,取w2=(0.1678,0.1485,0.1987,0.1892,0.1533,0.1425)T。

表6 考虑信息分布疏密的各企业最终评价值及排序结果

由表6可得出如下结论:4种密度算子中有3种密度算子得到的最优企业均为C2(PTF-DWGAOWA算子中最优企业为C6),这表明PTF-DM算子具有很好的稳定性。通常情况下,PTF-DWA算子的最终集结值大于PTF-DWGA算子的最终集结值,PTF-DM算子可以有效地应用于多属性决策中,且决策者可根据自身偏好自由选择相应的集结方法。

(4)PTF-DM算子与PTF集成算子的对比分析

为进一步验证PTF-DM算子的有效性,选择与何霞等[3]研究中提出的三种毕达哥拉斯三角模糊数集成算子(即毕达哥拉斯三角模糊数加权平均(PTF-WAA)算子、毕达哥拉斯三角模糊加权几何平均(PTF-WGA)算子与毕达哥拉斯三角模糊有序加权平均(PTF-OWA)算子)作对比研究,得到的最终评价值与排序结果如表7所示,同时图2反映了不同集结方法下各企业排序结果的变化趋势。

图2 不同集结算子下各企业最终评价值的变化

表7 不考虑信息分布疏密的各企业最终评价值及排序结果

从表7中可以看出,在运用上述3种经典算子实现信息集结时,最优企业均为C6,与表6中运用4种密度算子得到的最优企业(C2)不同,且整体排序结果有较大程度的波动。各企业整体排序结果有波动的关键原因在于密度算子实现了信息的二次集结,集结过程中受密度权重等要素影响使得评价值发生变动,进而影响排序结果。

从图2中可以观察出每家企业在不同集结算子下的最终评价值及其变化趋势,即各企业的最终评价值在3种经典算子中产生小范围波动,而在4种密度算子中变化明显。最终评价值变化明显的主要原因在于密度算子注重决策者对群体信息分布的偏好。决策者偏好确实可以影响最终的集结结果,因此考虑信息分布的疏密程度十分必要。

5 结论

毕达哥拉斯模糊集与密度信息集结是对信息表达及信息集成理念的新发展,本文是对二者的深度融合性研究。针对属性信息为PTFN的多属性决策问题,考虑到属性信息分布的疏密关系,提出PTF-DM算子并详细探讨其运用方法。具体而言,基于模糊参考理想法(FRIM法)的思想与得分函数,实现对PTFN的有效聚类,并运用熵值法建立规划模型确定密度权重。将PTF-DM算子与经典信息集结算子结合,构建出面向不同情境的具体集结算子,从而大幅拓展决策工具的选择空间。进一步的研究可从群体、时序背景切入,考虑立体信息结构下的多属性决策问题展开,实现对泛条件下的信息表达与集结研究。