Learning-Based Dynamic Connectivity Maintenance for UAV-Assisted D2D Multicast Communication
2023-11-06JingjingWangYanjingSunBowenWangShenshenQianZhijianTianXiaolinWang
Jingjing Wang ,Yanjing Sun,* ,Bowen Wang ,Shenshen Qian ,Zhijian Tian ,Xiaolin Wang
1 School of Information and Control Engineering,China University of Mining and Technology,Xuzhou 221116,China
2 XCMG Fire-Fighting Safety Equipment Co.,Ltd,Xuzhou 221004,China
3 School of Mines,China University of Mining and Technology,Xuzhou 221116,China
*The corresponding author,email: yjsun@cumt.edu.cn
Abstract: Unmanned aerial vehicles (UAVs) enable flexible networking functions in emergency scenarios.However,due to the movement characteristic of ground users(GUs),it is challenging to capture the interactions among GUs.Thus,we propose a learningbased dynamic connectivity maintenance architecture to reduce the delay for the UAV-assisted device-todevice(D2D)multicast communication.In this paper,each UAV transmits information to a selected GU,and then other GUs receive the information in a multi-hop manner.To minimize the total delay while ensuring that all GUs receive the information,we decouple it into three subproblems according to the time division on the topology: For the cluster-head selection,we adopt the Whale Optimization Algorithm (WOA) to imitate the hunting behavior of whales by abstracting the UAVs and cluster-heads into whales and preys,respectively;For the D2D multi-hop link establishment,we make the best of social relationships between GUs,and propose a node mapping algorithm based on the balanced spanning tree(BST)with reconfiguration to minimize the number of hops;For the dynamic connectivity maintenance,Restricted Q-learning(RQL)is utilized to learn the optimal multicast timeslot.Finally,the simulation results show that our proposed algorithms perform better than other benchmark algorithms in the dynamic scenario.
Keywords: cluster-head selection;whale optimization algorithm(WOA);balanced spanning tree(BST);multi-hop link establishment;dynamic connectivity maintenance
I.INTRODUCTION
Unmanned aerial vehicles(UAVs)have attracted much unparalleled attention and interest in industry and academia because of their flexibility and adaptability capabilities [1].The development of the Internet of Things (IoT) makes the case for UAV-assisted communication stronger than ever[2].Research on UAVassisted communication has been involved in environmental monitoring,agricultural irrigation,and intelligent transportation[3–5].
To be more specific,the issues addressed for the aerial communication networks,such as deployment,navigation,and control,are critical to further enhancing the energy-efficiency and coverage [6,7].Furthermore,some events including earthquakes and tsunamis have shown that the first 24 to 72 hours of a disaster are prone to be chaotic,and UAV-assisted communication is a reliable infrastructure for surveillance and recovery [8,9].Therefore,a reliable infrastructure of UAV-assisted communication should be considered.
1.1 Prior Works
Closer scrutiny of the related works reveals that the UAV is a pioneer in dealing with emergencies [10–12].If base stations (BSs) are damaged by disasters or emergencies,UAVs can be deployed rapidly as mobile relays for content sharing and information distribution due to their high-cost-effectiveness.There are some existing works investigating UAV-assisted communication.The authors in[13]proposed an architecture for UAV virtualization,which overcame the limitations of the short flight time of traditional UAVs,in turn allowing them to provide persistent services for multiple users.Songetal.in [14] proposed a flyand-communicate protocol,where the UAV disseminates some common information to all the ground users(GUs)and the completion time decreases monotonically with altitude.Mengetal.in [15] proposed a space pruning-based trajectory search (SPTS) algorithm by exploiting the geometric characteristic of the optimal inter-task UAV trajectory,which achieved substantially faster convergence and obtained a lower bound of the mission completion time.Furthermore,the optimization of the dynamic trajectory of UAVs is also investigated.The authors in [16] proposed a location-based k-means UAV clustering algorithm,which combined the mobility and relative location of the UAVs to enhance the reliability of the UAV network with limited resources.Dengetal.[17] proposed the clustering machine learning (C2ML) for multicast grouping and solved the UAV trajectory optimization problem by formulating an equivalent centroid-adjustable traveling salesman problem (CATSP).
To relieve the backhaul burden of UAVs,the authors in[18]proposed a transmission scheme in which multiple hovering UAVs relay data for a half of ground users (GUs) and share the spectrums with the other GUs that communicate with the BS directly.However,the interactions among UAVs,the BS,and GUs are complicated.Furthermore,this kind of framework only plays a significant role in enhancing spectral efficiency but ignores the transmission range.To extend the range of UAV-assisted communication,deviceto-device (D2D) communication technology is introduced.Wangetal.in [19] focused on joint caching placement and cache-enabled rescuers (CERs) deployment to maximize the effective capacity subject to delay-bounded quality of service (QoS) requirements by caching some imperative content at terrestrial CERs.The authors in [20] studied the tradeoff between the performance improvement of UAVs and the performance loss of ground D2D users when they reuse the same spectrum resources and obtained a reasonable spectrum sharing strategy through random geometric analysis,which can improve the total throughput.Jietal.in[21]jointly optimized the user association and UAV scheduling,transmission power,and UAV trajectory over a finite period in which both UAVs and D2D users are equipped with cache memory.The authors in [22] modeled the interaction between the operator,who allocated the activity policy of UAVs,and the content providers (CPs) as a cooperative game,in which they can exchange content via D2D links,thereby reducing content transfer cost and delay.
Other works stimulated by the movement characteristic of GUs have been approaching the optimal solutions in dynamic scenarios.Chenetal.in[23]utilized the machine learning framework of conceptor-based echo state networks(ESNs)to predict each user’s content request distribution and its mobility pattern,and then derived the optimal locations of UAVs as well as the content to cache at UAVs.The authors in [24]characterize the impact of GUs’mobility,propagation environment,and channel fading on the outage performance of UAV-assisted communication.
1.2 Motivation and Contributions
Considering that transmission delay is one of the most concerning problems in emergency communication,we hope to be able to solve this problem more thoroughly.As discussed above,related works have focused on the movement characteristic of GUs or dynamic trajectories of UAVs when solving optimization problems,but they did not make a further study on the dynamic evolution of the overall topology.In a nutshell,the dynamics are not just in the characteristics of the GUs themselves,but in the overall topology changes,i.e.,the social relationships and the status of transmission links among them.Therefore,we consider a UAV-assisted D2D multicast communication system with dynamic connectivity maintenance in emergency scenarios.
The trajectories of UAVs in[17]are the direct paths between the hovering positions in each group,and it is assumed that the UAVs can obtain global information.However,UAVs with limited storage capacities,which are used as relay devices for emergency communication,generally need patrol and probe to obtain global information.The trajectory optimization problem is usually non-convex,so the existing works utilize the convex approximation and heuristic methods to solve it [25].However,convex approximation algorithms usually have high computational complexity.Recently,since meta-heuristic optimization algorithms are easy to implement and can bypass local optima,they are becoming utilized in a wide range of problems covering different disciplines,especially in engineering applications.There are three main categories including evolution-based,physics-based,and swarm-based methods.Swarm-based algorithms preserve searching space information over iterations but evolution-based algorithms discard it.A new metaheuristic optimization algorithm,namely the Whale Optimization Algorithm(WOA),which is mimicking the hunting behavior of humpback whales,has been described and applied in wireless networks in [26].Therefore,we can consider adopting bionic algorithms to solve the trajectory-related optimization problem.
Considering the limited transmission capability of UAVs,the D2D forwarding mechanism is implemented on the ground to extend the communication range.Most of the related works deal with the movement characteristic of equipment by utilizing machine learning or Markov chains.The connectivity maintenance for UAVs has been well studied in [27,28]by utilizing their detection information and monitoring functions.However,connectivity maintenance for D2D links during the topology evolution has been neglected.It is worth mentioning that there are two important implications for this article in [27]: (i)a consensus-based action for enabling fast displacements with minimal topology changes by having all follower robots moving at a certain velocity;(ii) an automatic decrease of the minimum degree of connectivity,enabling an intuitive and dynamic expansion/compression of the formation.Motivated by the above contents on topology changes and connectivity and the work in [29,30],we focus on the physical and social graph extracted from topological changes including the GUs’movements from another perspective,in which the structure of the graph(tree)is analyzed and reconfigured in view of graph theory.
Compared to existing works,the main contributions are summarized as follows:
• We envision a real-world emergency communication scenario,where UAVs are deployed to work in place of damaged BSs.Considering the energy limitations,the UAVs first diffuse the information to the cluster-heads,then the social relationships among GUs are fully utilized to establish D2D links for the reliability of information transmission.Therefore,the optimization problem is decoupled into three subproblems: the cluster-head selection,D2D multi-hop link establishment,and dynamic connectivity maintenance according to the time division of the total delay,which allows for better capture of the characteristics in each transmission phase.
• We innovatively use the Whale Optimization Algorithm (WOA) to mimic the process of UAVs searching for cluster-heads by mimicking the hunting behavior of whales.Some virtual ground agents(GAs)are employed by UAVs for clusterhead searching process because UAVs do not have access to global information.The proposed WOA based cluster-head selection scheme(WBCSS)is more capable than the existing mechanisms in terms of solution stability and convergence speed in the UAV-assisted communication network.
• The D2D multi-hop link establishment based on the balanced spanning tree (BST) with reconfiguration algorithm is proposed to make the most of GUs’social relationships preserved,where reconfiguration covers three items: node mapping,edge construction,and node exchange.The proposed algorithm not only preserves most of the social relationships but also constructs the minimum number of hops and edges that are constructed,thereby reducing the transmission delay of GUs.Comparing existing work on UAVs’connectivity maintenance,we conduct complementary research on the aspect of maintenance of GUs’connectivity in UAV-assisted D2D multicast scenarios.To the best of our knowledge,this is the first work that BST is harnessed in UAV-assisted D2D multicast communication.
• Restricted Q-learning (RQL) is utilized for the cluster-head to learn the optimal multicast timeslot,in which the transmission delay of GUs is the lowest as the topology evolves.The D2D multihop link establishment algorithm combined with RQL is more robust to dynamic topological networks and can easily achieve dynamic connectivity maintenance.The simulation results verify both the adaptiveness and effectiveness of the proposed scheme while taking into account the interactions among UAVs and GUs in terms of physical locations,social relationships,and information forwarding abilities in highly dynamic scenarios.
1.3 Organization
The organization of this paper is as follows: In Section II,the application scenario for UAV-assisted D2D multicast communication is depicted.The algorithms for solving the delay minimization problem including WOA based cluster-head selection scheme,BST based D2D link establishment,and RQL based dynamic decision of timeslot for multicast are also illustrated in Section II.Numerical results and analyses for performance evaluation are shown in Section III.The conclusions are given in Section IV.
II.SYSTEM MODEL AND PROBLEM FORMULATION
As shown in Figure 1,we consider a communication scenario where ground users (GUs) are mobile and distributed randomly,and some UAVs are deployed to serve them due to the damage of base stations (BSs) for emergency communication.UAVsU={u1,u2,···,un}have different coverage capabilities measured in circular areas whose radiuses areRu={R1,R2,···,Rn},and they disseminate information to GUsD={d1,d2,···,dm}through line of sight(LoS)channels.Any two GUsdianddjare able to communicate with each other within a constrained circular area minthrough D2D links.
Since the storage capacities of UAVs are limited,it is unprocurable for each UAV to have global knowledge,such as all GUs’ physical locations of the last timeslot.We assume that each UAV transmits data to one GU in one task,and then returns over the ground vehicles(GVs)for charging or waits for the next transmission task.Then,the GU transmits the data to other GUs via multiple hops in the same cluster,which is divided according to the physical topology.To capture the interactions between GUs,we also focus on the social topology changes during a period of timeTafter releasing the task,in which the period is divided into several timeslots.Thus,an undirected hypergraph,|Et|≤n(Iis a finite set of indexes of nodes) is modeled for the social topology in timeslott.is termed as an undirected hyperedge,in which nodes communicate through multiple hops by utilizing their social relationships.For instance,the UAV firstly transmits information tod1,then a D2D multi-hop link can be established on the same undirected hyperedgewhich is composed of several GUsd1,d2,d3,andd4at timeslott.However,d4’s movement to another direction may cause his D2D link into be interrupted.Therefore,whetherd4should belong to cluster 2 or not is also one of the issues addressed in this paper.
Considering that the application scenario in this paper is the occurrence of an emergency,the optimization problem in this paper is to ensure that all GUs receive the messagefwhile minimizing the receiving time,i.e.the total delaydu:
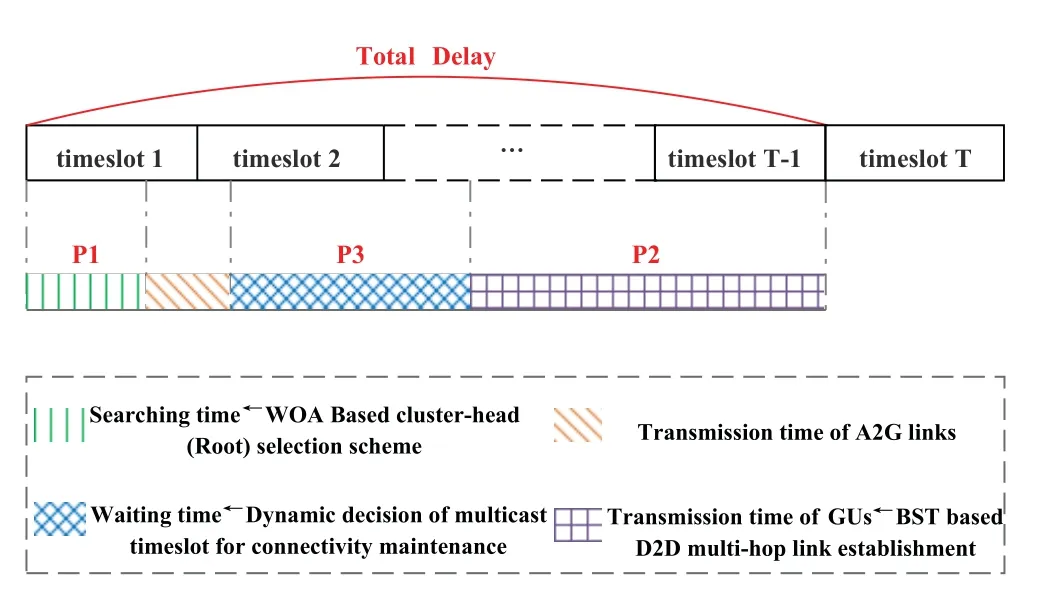
Figure 2.The diagram of time division during the transmission process.
whereαuandαdrepresent the path-loss exponents for the A2G link and D2D link,respectively.η0denotes the power gain of an LoS channel per unit distance.hm′,mdenotes the complex Gaussian channel coefficient which follows the distribution with a mean of 0 and a variance of 1.
As mentioned above,GUs in the clusterirequest messages in each timeslot.The UAV covering the cluster selects the most appropriate GU to be a ground relay,i.e.,cluster-head in a searching manner,and then relays the message to her.Afterwards,the rest GUs receive the messages through D2D multi-hop links.However,the movement characteristic of GUs may lead to the instability of D2D links.Therefore,according to the time division of the total delay in Figure 2,the optimization problemPis decoupled into three subproblems: the cluster-head selection (P1),D2D multi-hop link establishment(P2),and dynamic connectivity maintenance(P3),which are described in the following subsections.
2.1 WOA Based Cluster-Head (Root) Selection
Browsing the existing algorithms,the Whale Optimization Algorithm(WOA)is known for its fast convergence performance[26].In order to select clusterheads for UAVs (P1) more efficiently to minimize the delay,we resort to the WOA algorithm,which is highly competitive compared with state-of-the-art optimization methods.As a general assumption,the UAVs are regarded as humpback whales who live in groups,and cluster-heads are treated as preys.The whales have a special hunting method,including encircling prey,bubble-net attacking method,and search for prey.Due to the damage of the BS,the UAVs initially only have local information about the GUs,so they can utilize those GUs’ positional information in a creative way.By imitating the hunting behavior of whales,the UAVs employ some virtual nodes,i.e.,ground agents(GAs)G={g1,g2,···,gz},z≤m,to help with the search,and then the cluster-head(proximity of the best GAs)can be innovatively selected by the WOA.The initial positions of GAs(X,Y)are the same as the positions of partial GUs’,which is in line with the practical communication scenario,i.e.,UAVs cannot acquire global knowledge.In other words,the updates of GAs’ positions (the red nodes in Step 1 of Figure 3) can be the positions experienced by the UAVs searching for the cluster-heads.
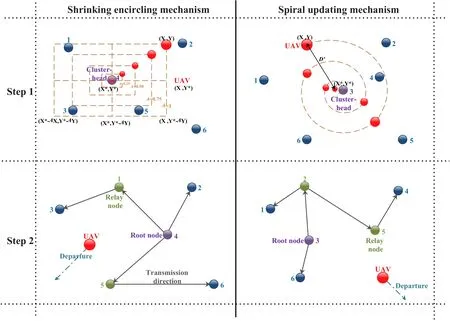
Figure 3.The illustration of UAV-assisted D2D multicast communication system in one cluster.
2.1.1 Encircling Prey
It is assumed that GUs are static in timeslott,and then move somewhere else in the next timeslott+1.The cluster-heads are the target preys for UAVs,whose GAs update their positions towards the preys over the course of iterations.This behavior is formulated by the following equations:
wheretidenotes the current iteration.represents the position vector of GA,and→X∗represents the position vector of the best GA.andare coefficient vectors calculated by
Step 1 of Figure 3 illustrates the rationale behind Eq.(5)for the communication scenario.Different coordinates around the cluster-head to be selected can be achieved with respect to the current position by adjusting the values ofandvectors.That the GA updates its position in the neighborhood of the best solutions intisimulates encircling the prey.
2.1.2 Bubble-Net Attacking Method (Exploitation Phase)
As mentioned before,humpback whales also attack the preys with the bubble-net strategy,which is composed of two approaches called shrinking encircling mechanism and spiral updating position.
The shrinking encircling mechanism is achieved by setting random values forin [-1,1] while linearly reducing the value ofover the course of iterations.Thus,the updated position of the GA can be found between the original position and the best GA.
Spiral updating position is achieved by mimicking the helix-shaped movement of humpback whales according to the distance between the GA located at(X,Y) and the best GA located at (X∗,Y∗).It can be calculated by
Considering that the two approaches are used simultaneously for whales,it is assumed that each mechanism is chosen with the probability of 50% to model the exploitation phase as follows:
wherepdenotes the probability.
2.1.3 Search for Prey(Exploration Phase)
In this phase,GAs are forced to move far away from a random GA by utilizing the shrinking encircling mechanism with the coefficient vector>1.So,the positionis replaced by the positionwhich is the position of the randomly selected GA.The searching space is extended to obtain a global solution.The exploration phase is modeled as follows:
The bubble-net attacking method concentrates on the local regional search by exploiting the current best GA,while the search for prey is to widen the searching space to achieve a global solution.The WOA algorithm is considered one of the most efficient optimization algorithms due to its good balance between exploitation and exploration.
The pseudocode of the WOA based cluster-head(root)selection scheme(WBCSS)is illustrated in Algorithm 1.The positions of the best GAs over the course of iterations are regarded as the projection of the UAV’s trajectory onto the ground (the earthy yellow dash line in Figure 3).We design the fitness function to calculate the fitness of each GA according to[32]:

The fitness function corresponds to the first part of the optimization problemP,which is a kind of unimodal function and has a minimum value.At the end of iterations,the outputs of Algorithm 1 are the locations of the best GAs in each cluster and the position of clusterhead,i.e.,the solution of the subproblemP1is:
The computational complexity of computing fitness function isO(NZ),whereNis the number of whales andZis the dimension of GAs.Since finding the positions of best GAs in each iterationIrequires computing the fitness once,the computational complexity of the algorithm isO(NZI).
2.2 D2D Multi-Hop Link Establishment
As shown in Figure 1,the UAVs transmit the information to the cluster-heads,then fly towards the GVs for charging or wait for the next transmission task.As shown in the Step 2 of Figure 3,GUs in the same cluster transmit the information via D2D links.It is noteworthy that not only the selection of cluster-head but also the social relationships among GUs will affect the D2D link establishment,i.e.,users with social relationships are more willing to forward information[33].Thus,the utilization of social relationships is no exception in this paper.
In order to ensure that all GUs can receive messages through D2D links,some works introduced an incentive mechanism,where nodes forward information to other nodes who have no social relationships with them after being rewarded [34,35].However,since the cluster can be divided according to the physical topology,we cannot guarantee that any two nodes in one cluster have a social relationship.So,the incentive mechanism should be a last resort,not a first line of defense due to its expensive cost.
Assuming that each GU has the same information forwarding ability,that is,she can mostly broadcast information tokGUs.To ensure that each node in the cluster can receive information with maximum use of social relationships,a node-mapping strategy based on the balanced spanning tree(BST)with reconfiguration is proposed for the D2D multicast transmission,where the root is the cluster-head obtained by Algorithm 1.
whereNadenotes the number of edges to be constructed in the BST.hdenotes the height of the BSTas well as the number of hops for GUs’transmission.The delay grows smaller as the height is shorter.denotes the preserve rate of the social edges in.The possibility of all GUs receiving the information becomes higher as the preserve rate is higher,i.e.the forwarding abilities of GUs are maximized.All nodes have exactlykleaves with the exception of the root node which has exactlyk+1 leaves[29].
To maximize the forwarding abilities of GUs,we resort to the BST to establish the D2D links and introduce the graph reconfiguration to solve the subproblemP2.The reconfiguration in our proposed algorithm innovatively includes three entries:
2.2.1 Node Mapping
To establish the D2D links,we introduce a nodemapping strategy with edge construction shown in Figure 4.In the first step of the process,we construct an initial BST according to a certainhandk.As shown in Figures 4(b),(c)and(d),differenthandklead to different numbers of nodes that are needed to form the BST,which has a great impact on the preserve rate of social edges and the number of edges that are constructed.In order to reduce the workload of this entry and reduce the total delay as much as possible,the number of BST’s nodes iskh-1(k+1),wherehis the minimum height that can constitute a BST.The next step is node mapping,i.e.,the mapping from nodeinonto the nodevfin.The mapping from the cluster-head onto the root nodehas been completed in 2.1.Then,the other nodes of the initial BST are determined by the level order according to the descending order of the nodei’s utility function(Φ):
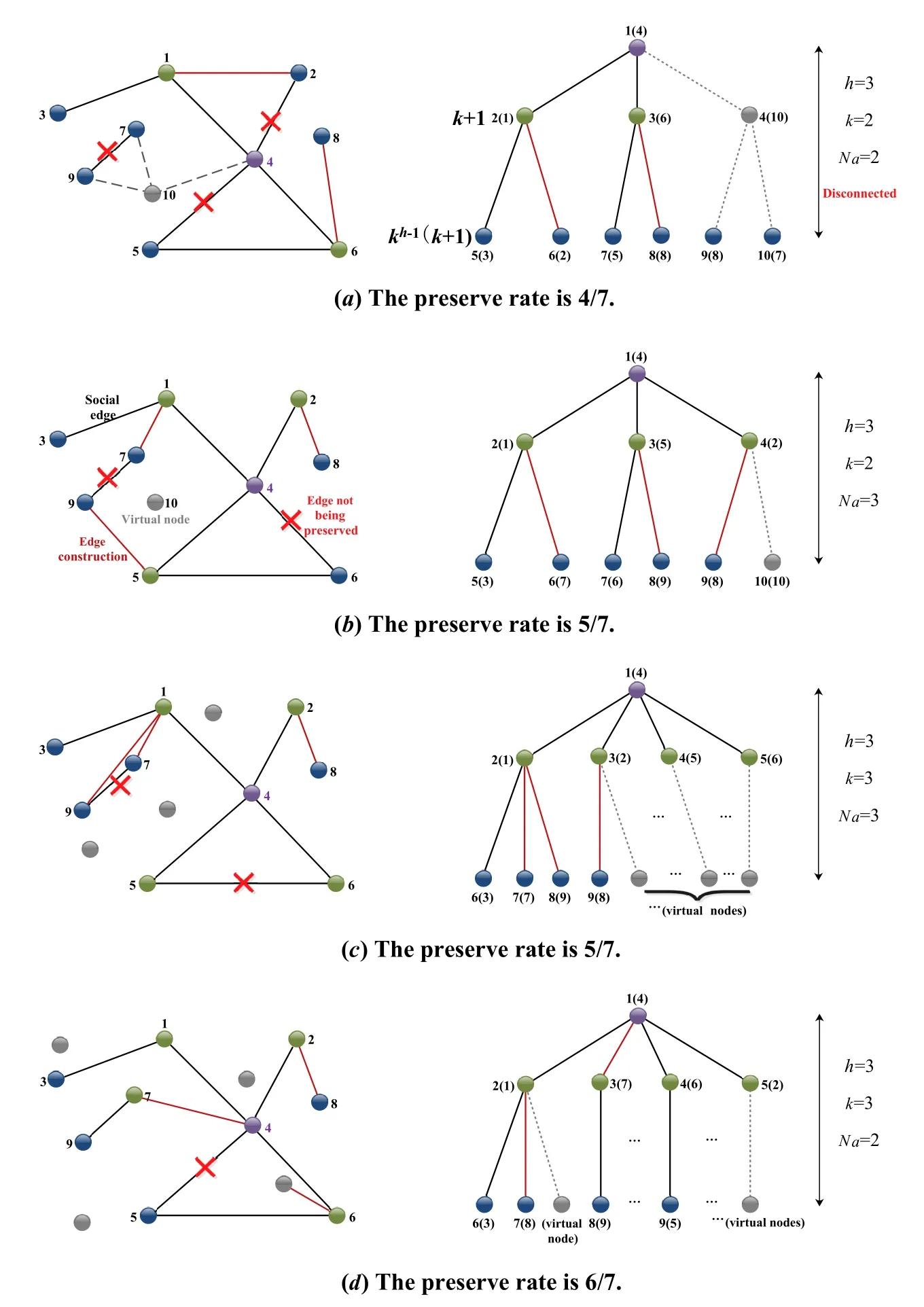
Figure 4.The D2D link establishment based on the BST with different h and k in cluster i.
wheredeg(i) denotes the degree of nodei.αandβare weighting factors and equal to 1/2.σ(i,npre) is a binary variable,which indicates whether the nodeiis connected with the current predecessor nodenprebeing traversed.However,since the number of nodes in the BST is not less than the number of nodes in the cluster,we add some virtual nodesNvthat are isolated,i.e.,their utility values are zero,to help complete the mapping.For example,Table 1 calculates all nodes’utilities in Figure 5(a) except the root node’s.When traversing to root node 1,we find that the utility values of node 2,node 3,and node 4 are the largest(the underlined parts),so 2,3,4 inare mapped to 2,3,4 in the BST.The node identifications in the BST are the sequence numbers generated in the level order,while the identifications in parentheses are the node numbers in the original topology.The virtual nodes can only be mapped to leaves or their predecessors that are also mapped from virtual nodes,otherwise,the tree will be disconnected shown in Figure 4(a).It turns out that Eq.(12)meets the requirements.
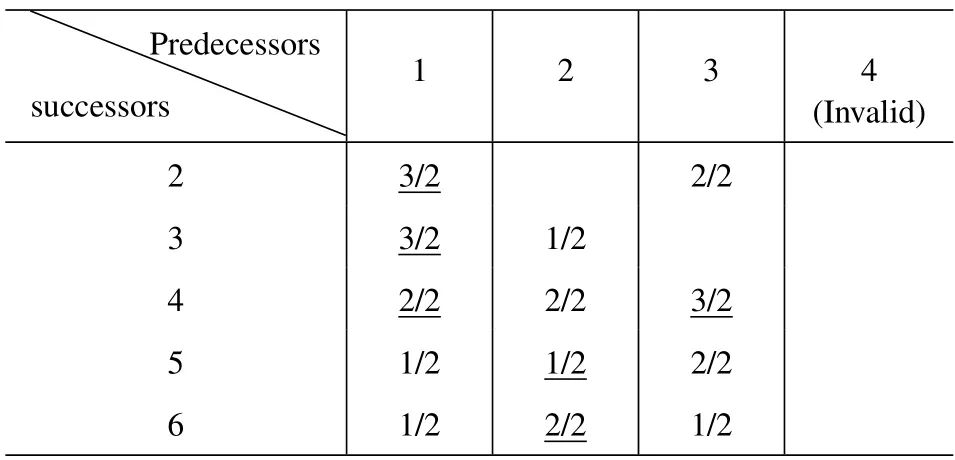
Table 1.Node exchanges for the BST reconfiguration.
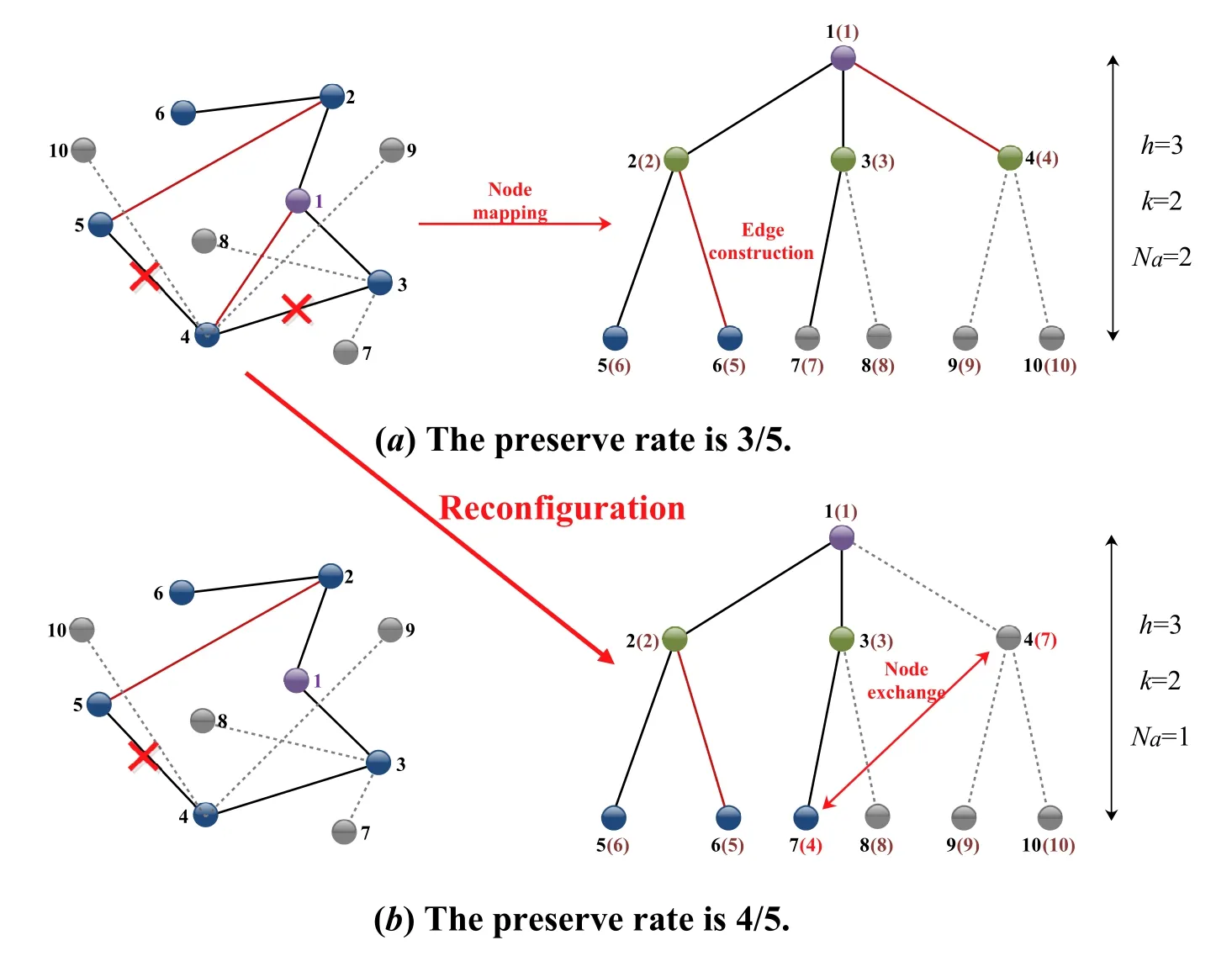
Figure 5.The diagram of the BST with reconfiguration in cluster i.
2.2.2 Edge Construction
To guarantee that each node in the cluster can receive the information,the multicast transmission topology is at least in 1-edge-connectivity,i.e.,there is at least one path between any two nodes in the BST.Therefore,we construct edges for GU nodes inaccording to the topology of the BST.Ifvf=Φ-1(vi)anduf=Φ-1(ui) are predecessor and successor inrespectively,as well as there is no social relationship betweenvianduiin,we construct an edge(ui,vi) for the D2D link establishment.As shown in Figure 4,the red lines are edges we construct.The black lines inandare social relationships and social edges that are preserved,respectively.The red crosses represent the social edges that are not preserved in the BST,i.e.,the social relationships that are not utilized for D2D multi-hop link establishment.The black dotted lines represent the virtual edges connecting the virtual nodes,which are only used to establish the complete BST and are not included in the calculations.By comparing Figure 5(a)and Figure 5(b),it is found that different node mappings lead to dif-ferent results regarding the number of edges that are constructed.
2.2.3 Node Exchange
To solve the subproblemP2,we conduct node exchange during the BST’s construction according to Eq.(12).Take an example as shown in Figure 5 and the corresponding Table 1,when the current predecessor comes to node 3 in,we find that the utility value of node 4 inhas increased compared to the previous two rounds(predecessors 1 and 2)while other GU nodes’did not increase.Therefore,we change node 4 and node 7 which was the successor of node 3 to reach our optimum.The preserve rate of social edges is increased by 1/3 compared with the non-node exchange,while the number of edges constructedNais reduced by 1.The D2D link establishment based on the BST with reconfiguration algorithm (BSTRA) we propose is shown in Algorithm 2.
Theorem 1.ThesolutionoftheproposedD2DmultihoplinkestablishmentbasedontheBSTwithreconfigurationalgorithmisconvergentandstable.
Proof.Theorem 1 can be proved by contradiction readily as follows.For a GU nodeui,we get and verify her predecessoruvby using Eq.(12) in Algorithm 2.If the current solution were unstable,there should be someone else,such as another GU nodeukthat can replaceuv,i.e.,Ud(i,uk)>Ud(i,uv),which goes against our proposed algorithm.Therefore,as the iteration proceeds,the algorithm converges into a stable solution.
The computational complexity of the level order for the BST isO(W),whereWis the width of the tree.Considering the worst case,the computational complexity of each node being replaced once isO(M2).
2.3 Dynamic Decision Algorithm Based on RQL
Since GUs move randomly and the arrival of multicast missions is unpredictable,the physical and social topology changes cannot be ignored.However,if the multicast behavior is triggered without observing the topology of GUs as soon as the cluster-head receives the information,then we may construct too many edges for the GUs’ multi-hop transmission or the delay of D2D links is too large.Like the GUd4in Figure 1,his movement makes both the physical and social topology change greatly,which affects the transmission link establishment,or even worse,leads to a transmission interruption.This shows that it is quite important to determine which timeslot to carry out the multicast for GUs to reduce the total delay.Therefore,we propose a dynamic decision of multicast timeslot algorithm with connectivity maintenance based on the adaptive batch-based framework [36].The objective of this section(P3)is to find an appropriate multicast timeslot,in which the third part of the total delay can be minimized,so we turn the problem into a dynamic decision problem based on Restricted Q-learning(RQL).

As shown in Figure 6,the physical and social topologies between timeslott=1 and timeslotTstand for the states,which can be splitted into batches.This kind of sequential decision-making problem,i.e.,batch splitting process,can be modeled as a Markov decision process (MDP),which is composed of state space,action space,reward function,and time horizon.By interacting with the environment,i.e.,the dynamic topologies,the actions,i.e.,the multicast timeslot selection,will be taken according to the reward.To find the optimal strategy of multicast timeslot selection,we apply RQL to split batches.A particular description of RQL is given in the following parts,including state representation,restriction principle,and state&action reformulation.
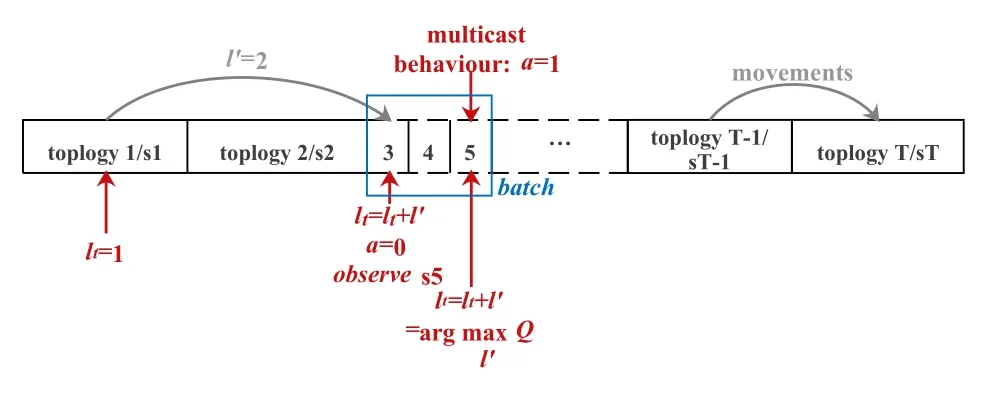
Figure 6.Dynamic decision process for multicast behaviour based on RQL.
2.3.1 State Representation
We represent each state by the topology containing the number of nodes,the positions of nodes,and the relationships among them,rather than using a state-action table to record the Q-function as in traditional Qlearning algorithms for the smaller size of state space.The size of the state space of our MDP is infinite,so we cannot record every state-action pair.Another reason why the state-action table is not used is that it is almost impossible for GUs to encounter the same state twice.As there areM-NGU nodes waiting on the topology,the size of state space is(M-N)2.
2.3.2 Restriction Principle
We exploit the restriction principle to reduce the size of the strategy space in this adaptive framework based on RQL,which is exponential of the time horizon in traditional Q-learning.According to Algorithm 2,the strategies in the restricted space splitted by a batch satisfy that the distance between two adjacent nodesiandjis less than min{}for each cluster(BST)formed by multiple links.
2.3.3 State&Action Reformulation
The original action space can be denoted as{0,1}in each timeslot.To meet the restriction principle of RQL,we definel′∈[lmin,lmax]as the expected length of the current batch.Both of the upper and lower bounds satisfyl′≤D.Dis the maximum duration of a transmission task.Our opportunity of multicast decision only occurs when the batch length is no smaller thanlmin.With the above theories in heart,the reward for the multicast timeslottis:
wherea1 andb1 are the positive tradeoff factors,satisfyinga1+b1=1.We can adjust the weights of our concern for the waiting time and delay of D2D multi-hop links.In order to reduce the total delay,it is reasonable for the cluster-head to wait forl′timeslots during the dynamic evolution of the physical and social topology over time.RQL is introduced to make the decision of the multicast timeslot in dynamic scenarios more intelligent.As shown in Figure 6,after two rounds of batch splitting by settingl′=2,the splitting point corresponding to the maximum feedback is found,i.e.,the topology at timeslott=5 is most suitable for the multicast behavior.
To facilitate batching,the action of executing the multicast behaviora∈{0,1}is replaced byl′∈[lmin,lmax].The updates of Q-values forandare as follows:
The dynamic decision of the multicast timeslot algorithm based on RQL (DTBRQL) is shown in Algorithm 3.Firstly,we initialize the batch and set the Q-values of the situations wherel>l′to be 0.Then,we conduct actiona=0 forlmin-1 timeslots and observe the situation atlmintimeslot.With the passage of iterations,Q-values are updated according to the state,i.e.,the dynamic evolution of the physical and social graph.The decision of the multicast timeslot can be controlled by adjusting the boundaries of the batch.The timeslotwith the largest Q-value will be denoted asa=1,i.e.the GUs carry out the D2D multihop link establishment at this timeslot.,h,Na,and the preserve rate are the outputs of Algorithm 2 as well as the inputs of Algorithm 3 whose output is the delay of D2D multi-hop links at the timeslot

The space complexity of RQL,i.e.,the memory size to store the tabular Q-function for GUs isThe computational complexity to execute Algorithm 1 and Algorithm 2 on the physical and social graph with at mostNnodes per time is at mostO(M2I)becauseN≪M.The proposed algorithm tends to be more robust to dynamic topological networks because the changes in topology only affect the topology in each cluster.The nodes can quickly learn the next multicast timeslot with relatively low computational complexity.
III.SIMULATION RESULTS
In this section,simulations of the proposed dynamic decision of multicast timeslot algorithm based on RQL(DTBRQL) are conducted in addition to WOA based cluster-head(root)selection scheme(WBCSS)and the D2D multi-hop link establishment based on the BST with reconfiguration algorithm (BSTRA).The main simulation parameters are shown in Table 2.Thereinto,the heights of the UAVs cannot exceed 100 meters [17].Indicators involving communication,such asη0,N0,αu,and so on,are all referred to[11].The probability of social relationships between any two GUspsis adjustable between 0 and 1.The information forwarding ability of GUs is denoted byk,which equals to 3 for the cluster-heads and 2 for other GUs.
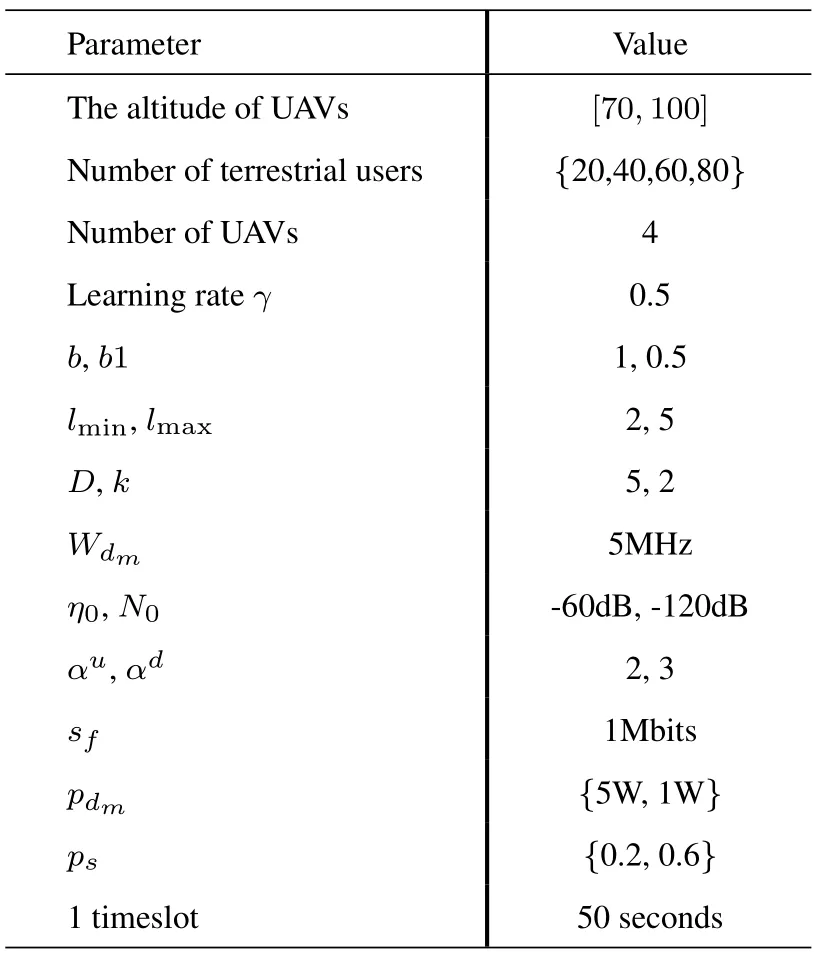
Table 2.Simulation parameters setting.
To verify the performance advantage of WBCSS,we adopt different benchmark algorithms for solving the subproblemP1,i.e.,the cluster-head searching.Since our proposed algorithm belongs to natureinspired meta-heuristic algorithms,which are composed of three main categories: evolution-based,physics-based,and swarm-based methods,we adopt three representative algorithms including Random Walk Algorithm with Restart (RWWR) [37],Ant Colony Optimization (ACO) algorithm [38],and Genetic Algorithm (GA) [39] for the performance comparison.As shown in Figure 7,we conduct simulations in one cluster under the above four algorithms.
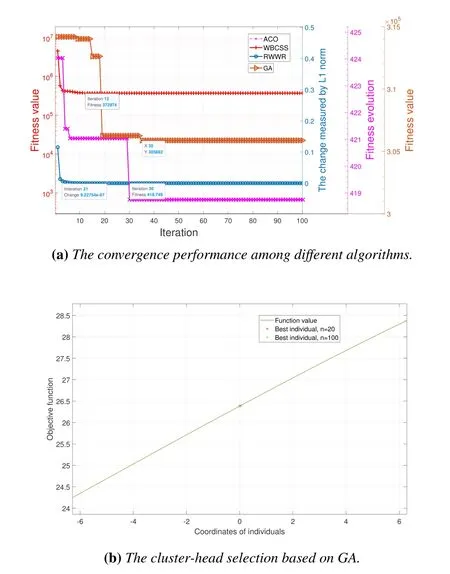
Figure 7.Performance comparison among different algorithms for cluster-head selection.
The value of coordinatesx1andx2is [-100,100],and four clusters are formed according tox1∈[-100,0],x2∈[0,100];x1∈[-100,0],x2∈[-100,0];x1∈[0,100],x2∈[0,100];andx1∈[0,100],x2∈[-100,0].We present the simulation results in the first cluster,where the hovering position of the UAV in the first cluster is(-28,26,71).Thereinto,the number of GUs in Figure 7 is 20 while the numbers of GUs in the other figures are not unique.
Figure 7(a) presents the convergence performance of different algorithms including WBCSS,RWWR,and ACO algorithms for UAVs’ searching for the cluster-heads.
As for the Ant Colony Optimization (ACO) algorithm,the inspiring factor and the pheromone concentration are denoted by the reciprocal of distance between the GA and the UAV and the reciprocal of delay of the A2G link,respectively.The fitness value of the ACO algorithm is the shortest distance for the UAVs searching for the cluster-heads to minimize the delay of the A2G link.
As for the Random Walk Algorithm with restart(RWWR),the probabilities for GU nodes are denoted byp(0),and the probabilities for GA nodes are denoted byp(1).The random walk is defined as:
whereris the probability of random walk in every time step at GU nodes.Wdenotes the similarity function between nodeiand nodej.In this simulation,the similarity function is denoted byW=1/|sf/Ri-sf/Rj|,wheresf/Rirefers to the transmission delay from UAV node to GU or GA nodei,i.e.,the delay of the A2G link.The parameterris set to 0.5.When theL1norm calculated by the change betweenp(t) andp(t+1) is less than a cutoff 10-6,the random walk is considered stable[37].
As for the Genetic Algorithm(GA),the population equals to 20,consisting of 10 GUs and 10 GAs.Both the crossover probability and mutation probability are 0.5.The objective function is the same as the proposed WBCSS’s,i.e.,Eq.(9).
Although these four algorithms have different measurement indexes on convergence,their parameter settings are all related to the delay of the A2G link as described above.As shown in Figure 7(a),the convergent steps of the WBCSS,the ACO,the RWWR,and the Genetic Algorithm (GA) are 12,30,21,and 35,respectively.It is clearly observed that our proposed WBCSS has the fastest convergence rate.What’s more interesting is that the UAVs’trajectories of other algorithms are all straight lines,but our proposed algorithm arranges both straight lines and curves for UAVs’trajectories,which is more in line with the reality of UAV patrols.
In addition,as shown in Figure 7(b),the output(marked as a star)of the Genetic Algorithm(GA),i.e.,the best individual (cluster-head),is greatly affected by population sizen.Because GA does not use the external information in the searching process,i.e.,only takes each individual’s fitness function as the basis for the search,it is unstable in the investigated scenario.Since the initial GAs’ positions are the positions of partial GUs,the output of WBCSS can be unique according to the position updating mode of WOA after iterations.For example,the positions of best 20 GAs in the clusterx1∈[-100,0],x2∈[-100,0](the outputs of WBCSS) are -1.2344,-0.36605,-0.75265,-1.2011,-0.1539,-1.2451,-0.68183,-0.41169,-1.094,-0.81645,-0.95121,-1.5417,-0.52223,-1.207,-0.64265,-0.84251,-0.54546,-0.34877,-0.8381,-0.899,and the position of the corresponding cluster-head is[-16,-11].
The computational complexity of the ACO isM(M-1)×Z×I/2.The RWWR is very dependent on the step size.The larger the step size is,the larger the initial space to find the optimal solution is,i.e.,the more iterations are.Therefore,as the scale of the application scenario expands,the proposed WBCSS is one of the most effective algorithms for the clusterhead selection process and is adaptive for the dynamic scenario with lower complexity.
The number of edges that are constructed for the D2D multi-hop link establishment is investigated among three conditions: the proposed BSTRA,BSTRA without node exchange,and BST with random mapping.In this step,we add several virtual nodes for the initial graph to generate a multicast BST.The solutions to the subproblemP2areh=2,h=2,h=3,andh=3 respectively when the numbers of GUs in the first cluster are 5,10,15,and 20,and the specific numbers of edges that are constructed are shown in Figure 8.It can be seen that the number of edges the proposed BSTRA obtained is lesser than that of the other two algorithms obtained.Besides,it is worth mentioning that when the numbers of GUs are 15 and 20,we don’t need to construct extra edges.This illustrates that if there are enough social relationships(edges),the construction of edges for D2D multi-hop links can be avoided as long as the graph reconfiguration is properly utilized.
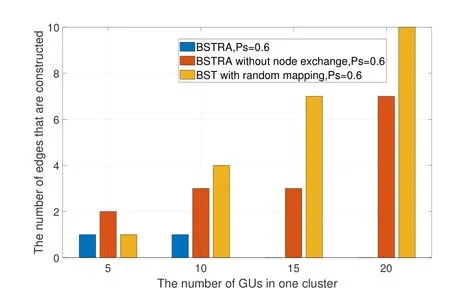
Figure 8.The number of edges that are constructed among different algorithms in one cluster.
The preserve rate is another measurable indicator in the subproblemP2.We compare the preserve rates of three algorithms which are the same as the algorithms mentioned above under different probabilities of social relationships.It is found that in Figure 9,the higher the social probability is,the more unutilized social edges will be.Therefore,BSTRA with thePs=0.6 has a lower preserve rate than that withPs=0.2.The preserve rate decreases as the number of GUs increases.Nevertheless,when the social probability is 0.6,the preserve rates obtained by BSTRA without node exchange and BST with random mapping with 10 GUs are slightly higher than that obtained by them with 5 GUs.The reason is that as the number of GUs increases,the number of social edges in the BST also increases.However,if the number of GUs grows to a point where the number of social edges grows faster than the number of the BST’s edges,the preserve rate drops.Furthermore,when the probability of social relationships is fixed,the preserve rate the proposed BSTRA obtained is significantly higher than that of the other two benchmark algorithms.
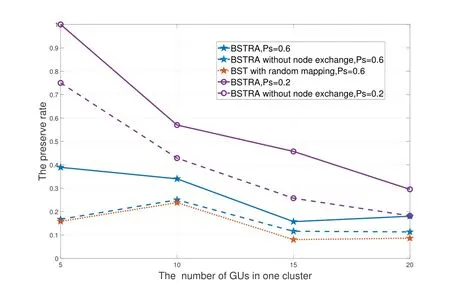
Figure 9.The preserve rate among different algorithms in one cluster.
Since our optimization problem includes minimizing the total delay,we take the outputs of Algorithm 2 as the partial inputs of Algorithm 3 to achieve dynamic connectivity maintenance for the dynamic scenario.Therefore,we also compare the delay of different algorithms under different probabilities of social relationships.As shown in Figure 10,when the probability of social relationships is fixed,the delay the proposed DTBRQL obtained is much lower than that of algorithms without RQL.What is interesting is that the delay is lower with 10 GUs than that with 5 GUs.The reason is that even though they have the same height in the BST,the GUs are more dispersed when the number of GUs is 5,resulting in a relatively long transmission distance.Therefore,the proposed DTBRQL can availably capture the GUs’ movement characteristics,analyze dynamic topological changes,and find the optimal multicast timeslot by utilizing RQL.
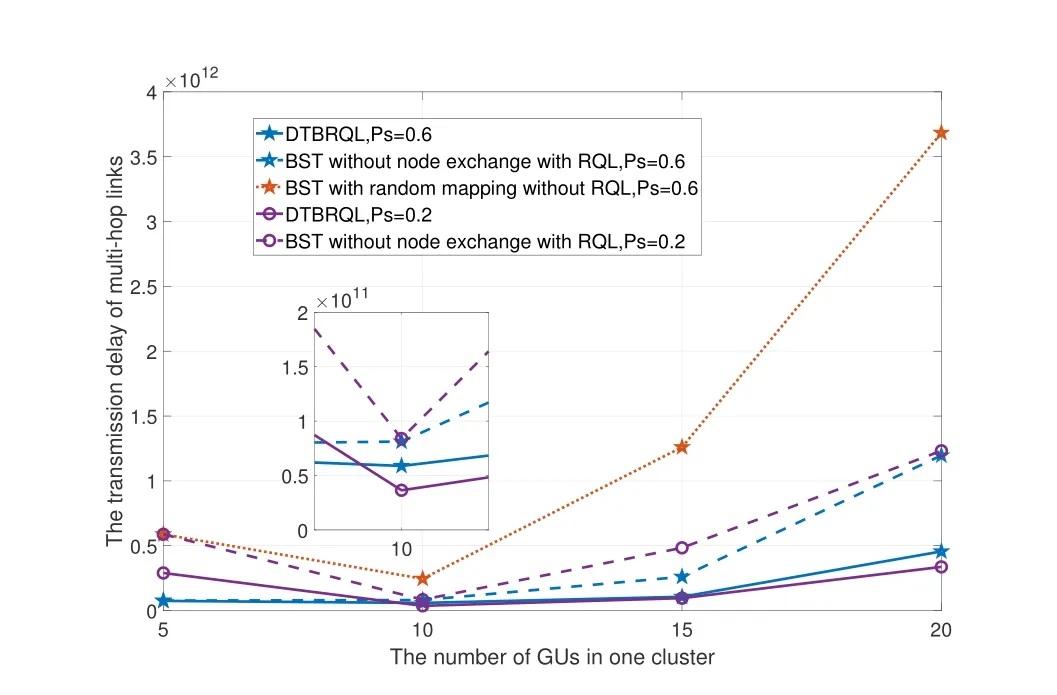
Figure 10.The transmission delay of multi-hop links among different algorithms in one cluster.
IV.CONCLUSION
In this paper,we have investigated the reliability and low-delay transmission for UAV-assisted D2D multicast communication in emergency scenarios.According to the time division on the physical and social graph abstracted from the network,we decoupled the optimization problem into three subproblems: clusterhead selection,D2D multi-hop link establishment,and dynamic connectivity maintenance.The cluster-head selection problem was formulated as the hunting behavior of whales by treating the cluster-head as UAVs’prey.To minimize the number of hops and edges that were constructed as well as preserve most of the social relationships for information transmission among GUs,a D2D multi-hop link establishment based on the BST with reconfiguration algorithm has been proposed.As the physical and social topology has been changing over time,RQL was utilized to learn the optimal multicast timeslot for dynamic connectivity maintenance.Simulation results were a testament to the validity,adaptation,and efficiency of our proposed algorithms in dynamic scenarios.
ACKNOWLEDGEMENT
This work is part supported by the Future Scientists Program of China University of Mining and Technology(2020WLKXJ030)and the Postgraduate Research&Practice Innovation Program of Jiangsu Province(KYCX20_1993).
杂志排行
China Communications的其它文章
- SR-DCSK Cooperative Communication System with Code Index Modulation: A New Design for 6G New Radios
- Sparsity Modulation for 6G Communications
- Sparse Rev-Shift Coded Modulation with Novel Overhead Bound
- Reconfigurable Intelligent Surface-Based Hybrid Phase and Code Modulation for Symbiotic Radio
- Model-Driven Deep Learning for Massive Space-Domain Index Modulation MIMO Detection
- Modulation Recognition with Frequency Offset and Phase Offset over Multipath Channels
