Reconfigurable Intelligent Surface-Based Hybrid Phase and Code Modulation for Symbiotic Radio
2023-11-06SongBaiQiangLiDonghongCai
Song Bai,Qiang Li,Donghong Cai
College of Information Science and Technology,Jinan University,Guangzhou 510632,China
*The corresponding author,email: qiangli@jnu.edu.cn
Abstract: Reconfigurable intelligent surface (RIS)-assisted symbiotic radio is a spectrum-and energy-efficient communication paradigm,in which an RIS performs passive beamforming to enhance active transmission,while using the electromagnetic waves from the active transmission for additional information transfer (i.e.,passive transmission).In this paper,a hybrid RIS-based modulation,termed hybrid phase and code modulation (HPCM),is proposed to improve the reliability of RIS-assisted symbiotic radio.In RIS-HPCM,the RIS simultaneously performs direct sequence spread spectrum and passive beamforming on incident signals.Moreover,both the spreading code and phase offset are exploited to carry the RIS’s own information.A low-complexity detector is designed,in which the receiver first detects the spreading codes and then demodulates the constellation symbols.We analyze the bit error rate(BER)performance of RIS-HPCM over Rician fading channels.BER upper bounds and approximate BER expressions are derived in closed-form for maximum-likelihood and low-complexity detectors,respectively.Simulation results in terms of BER verify the analysis and show the superiority of RIS-HPCM over the existing RIS-based modulation.
Keywords: reconfigurable intelligent surface;symbiotic radio;index modulation;direct sequence spread spectrum;performance analysis
I.INTRODUCTION
A reconfigurable intelligent surface (RIS) has a large number of low-cost and low-power passive reflecting elements,whose reflection coefficients can be manipulated to flexibly control the propagation environment[1,2].By judiciously adjusting the reflection coefficients,RISs have found a wide range of applications in the field of wireless communications [3].Among them is symbiotic radio(SR).In RIS-SR,the RIS not only enhances active radio transmission but also enables passive transmission by resorting to the radio waves of the active transmission [4,5].In essence,the passive beamforming of the RIS is performed according to the passive information to be sent.In such a manner,the passive transmission dispenses with the adoption of complex radio-frequency chains and the occupancy of additional spectrum.Therefore,RISSR is a spectrum-and energy-efficient communication paradigm,and is expected to be a promising solution to Internet of Things networks.
Index modulation [6–8] that uses the activation states of some resources/building blocks for information embedding is a key enabling technology for RISSR [9].The author in [10] proposes the RIS with spatial modulation (RIS-SM) scheme,which embeds passive information into the receive antenna index associated with the maximum received power via RIS’s beamforming.To improve the data rate,in [11],the RIS is virtually partitioned into two parts,and they perform beamforming independently to steer the inphase (I) and quadrature (Q) components of reflected signals to two receive antennas respectively as in QSM[12],where the indices of the two antennas are determined by two different data streams.In[13],the RISSM scheme is integrated with conventional transmit SM.Reference [14] proposes to use different phase shift matrices of an RIS to carry passive information in RIS-aided multi-input-multi-output(MIMO)systems.In [15],each RIS element is set to be active or inactive,which conveys one bit of passive information.To avoid the power loss resulting from inactive elements,the authors in[16]propose to activate all RIS elements by applying two orthogonal states,i.e.,I-and Q-state,and use the positions of the elements with the I-state to convey the passive information.Further,the authors in [17] propose to encode passive information into the number rather than positions of the elements with the I-state,achieving higher reliability in terms of passive transmission.Apart from index modulation,RISs can implement amplitude and phase modulation to transmit passive information by exploiting the capability of reconfiguring the amplitude and phase responses of channels.Specifically,in[18],the RIS elements are grouped into two halves,each of which is regarded as one antenna,and then Alamouti space time block coding is implemented based on the two virtual antennas.In[19],double-ring phase shift keying (PSK) is performed at the RIS by taking into account the constellation used at the active transmitter.By simultaneously adjusting the ON/OFF state and the phase shifts of an RIS,a hybrid amplitude-and phasemodulation scheme is introduced in [20].In contrast to[10,11,13–20]that consider the scenario of centralized reception for the active and passive information,[21,22]propose RIS-SR with distributed reception for MIMO and single-antenna systems,respectively.
It is worth mentioning that RIS-SR applies to many practical scenarios.For example,with RIS-SR,home sensors in the smart home can transmit messages to a smart phone by relying on the radio signals from the Wi-Fi access point(AP).However,there are still some challenges in existing RIS-SR systems,such as the involvement of complex non-convex optimizations,relatively poor error performance for the passive transmission,and the requirement of multiple receive antennas.Moreover,the passive transmission is often achieved at the cost of the performance of active transmission.Motivated by these observations and the capability of configuring an RIS at a chip rate [23,24],in this paper we employ an RIS to simultaneously perform passive beamforming and direct sequence spread spectrum(DSSS),and propose a novel RIS-based modulation,termed hybrid phase and code modulation(RISHPCM).The main contributions of this paper are summarized as follows:
• In RIS-HPCM,the phase shifts and spreading codes are jointly used to convey passive information.Moreover,the phase shifts are optimized in terms of both passive beamforming and information transmission.In addition to the optimal maximum-likelihood (ML) detector,a lowcomplexity (LC) yet near-optimal detector is designed.
• We analyze the bit error rate(BER)performance of RIS-HPCM with the ML and LC detectors over Rician fading channels.Upper bounds on the BERs of both active and passive transmission are derived in closed form.Extensive computer simulations are conducted to verify the analysis and the superiority of RIS-HPCM over RIS-SM.
The rest of this article is organized as follows.In Section II,we present the system model of RISHPCM,including the design of information modulation and signal detection.Section III analyzes the BER performance of RIS-HPCM with ML and LC detectors.Simulation results are given in Section IV.Section V concludes this paper.
Notations: Column vectors and matrices are denoted by lowercase and uppercase boldface letters,respectively.ℜ{·} and ℑ{·} return the real and imaginary parts of a complex number,respectively.j=is the imaginary unit.(C)N(µ,σ2) represents the(complex)Gaussian distribution with meanµand varianceσ2.E{·}andVar{·}denote expectation and variance,respectively.The probability of an event,the probability density function (PDF),and cumulative distribution function(CDF)of a random variable are denoted by Pr(·),p(·),andF(·),respectively.Q(·)represents the GaussianQ-function.∠(·)denotes the phase of a complex number.∥·∥denotes the 2-norm of a vector.(·)Tand (·)Hdenote the transpose and Hermitian transpose,respectively.1Ndenotes anNdimensional all-one vector.TheN×Nidentity matrix is symbolized by IN.1F1(·;·;·)denotes the confluent hypergeometric function.
II.SYSTEM MODEL
Figure 1 depicts the system model of RIS-HPCM,in which a single-antenna AP transmits active information ofb0=log2Mbits viaM-ary PSK symbol-bysymbol with guard intervals in between,to a singleantenna user with the aid of an RIS.The RIS,consisting ofNreflecting elements,simultaneously reflects the signal from the AP and conveys passive information to the user.The RIS is connected to and configured by a controller that is located in the proximity of the AP,thus facilitating the feedforward link from the AP to the controller [25].The reflection coefficient for thei-th reflecting element at the timetis given byϕi(t)=ejθi(t),wherei=1,...,N,andθi(t) is the time-varying phase shift that can be arbitrarily adjusted by the RIS controller in the interval[0,2π).For ease of exposition and to model the scenario with obstructions between the AP and the user,we assume that a direct link from the AP to the user does not exist [26].Note that the proposed modulation technique also applies to the scenario with a direct link,which will be considered in future work.The channels from the AP to the RIS,and from the RIS to the user are described by g=[g1,...,gN]T∈CN×1and f=[f1,···,fN]T∈CN×1,respectively,wheregiis the channel coefficient from the AP to thei-th reflecting element,andfidenotes the channel coefficient from thei-th reflecting element to the user.In this paper,quasi-static Rician fading channels are considered,i.e.,we have
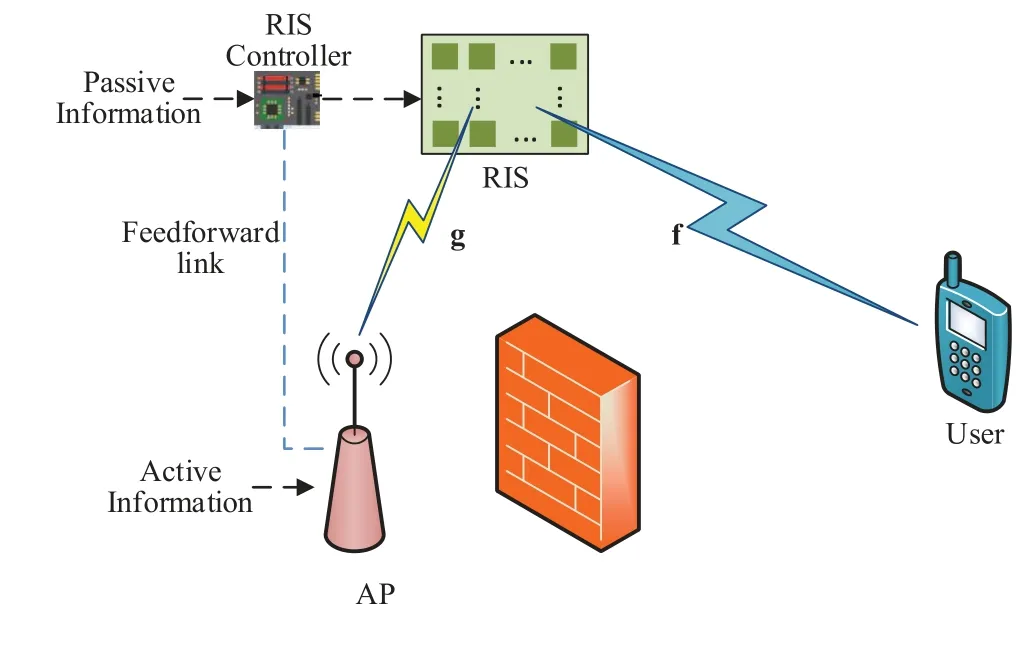
Figure 1.System model of RIS-HPCM.
whereKis the Rician factor for both the AP-RIS and RIS-user channels.gLosand fLosrepresent the deterministic line-of-sight components of the AP-RIS and RIS-user channels,which are assumed to be gLos=fLos=1N,respectively [16].gNLoS∼CN(0,IN)and fNLoS∼CN(0,IN) are the non-line-of-sight components of the AP-RIS and RIS-user channels,respectively.
The received signal at the user can be given by
wherexis anM-ary symbol drawn from a normalized PSK constellationM,andw(t) stands for the additive white Gaussian noise at the user.Without loss of generality,let us focus on one symbol period,namelyt∈[0,Ts],whereTsis the symbol period.At the timet∈[0,Ts],the phase shift for thei-th RIS element is composed of two parts,i.e.,
whereξiis the time-invariant part of the phase shift for thei-th reflecting element,andφ(t) is the timevarying part of the phase shift for all reflecting elements.By putting(4)into(3),we arrive at
Samplingy(t)at the rate of 1/Tcleads to
wheren=0,...,L-1,Tc=Ts/Lis the chip period,andLis the spreading factor.We can rewrite(6)into
where y=[y0,...,yL-1]T=[y(0),...,y((L-1)Tc)]T,c=[c0,...,cL-1]T=[ejφ(0),...,ejφ((L-1)Tc)]T,and w=[w0,...,wL-1]T=[w(0),...,w((L-1)Tc)]T
with the distributionCN(0,N0IL).
2.1 RIS-Based Modulation Design
By recalling that spreading codes,such as Zadoff-Chu and Walsh codes,have a unity amplitude and thus can be acted by reflection coefficients of an RIS,c in (7)can be treated as a spreading code andxc as the implementation of DSSS onx.Therefore,by resorting to the concept of code index modulation[27],we can employ c for information transfer.Specifically,we construct a spreading code setZ={c0,...,cL-1}that includesLspreading codes,and then select a spreading code fromZas c according tob1=log2Lbits,whereLis set to be an integer power of 2.
To enable LC detection at the user,the spreading codes inZshould be orthogonal to each other,and the maximum size ofZisL.For Walsh codes,the(l+1)-th spreading code inZ,i.e.,cl,is the(l+1)-th column of theL×LHadamard matrix,wherel=0,...,L-1.For Zadoff-Chu codes,Zis derived by cyclically shifting a basic Zadoff-Chu sequence by 0,...,L-1 positions.The mapping and demapping between theb1bits and c can be easily implemented by the natural binary code.
On the other hand,from (7),ξican be set toξi=-∠fi-∠gi+ζto maximize the received power,whereζ∈[0,2π)is a phase offset.In this case,(7)reduces to
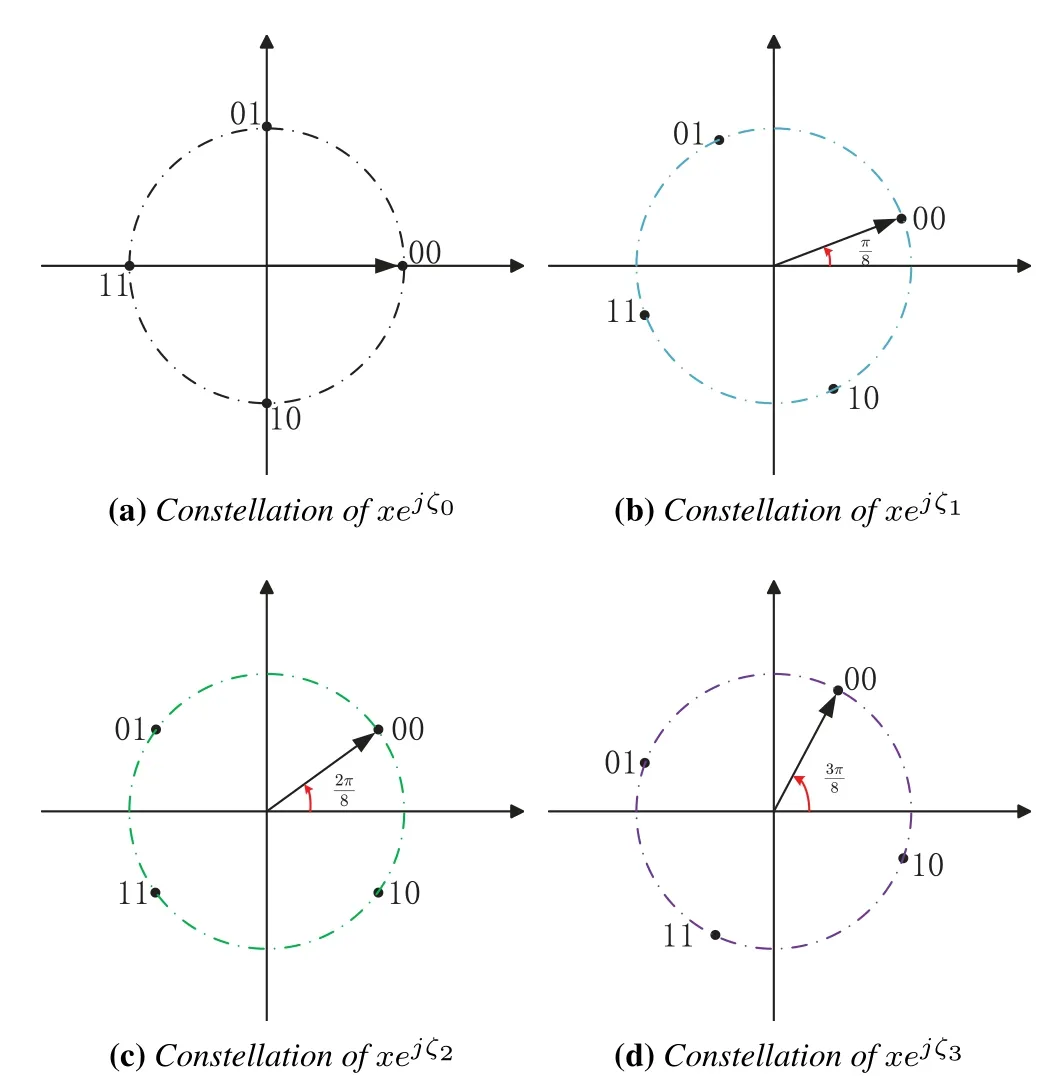
Figure 2.The constellations of xejζ0,xejζ1,xejζ2,and xejζ3,where M=4,P=4,ζ0=0,ζ1=π/8,ζ2=2π/8,and ζ3=3π/8.
2.2 Signal Detection Design
For signal detection,the receiver should detect the constellation symbolx,the spreading code c,and the phase offsetζ.In this section,we develop the optimal ML and a near-optimal LC detectors.
2.2.1 ML Detector
From(8),the optimal ML detector makes a joint decision onx,c,andζby searching all possible combinations of them,namely
2.2.2 LC Detector
In this detector,the detection process consists of two steps.In the first step,the spreading code is estimated by exploiting the orthogonality of spreading codes.In the second step,the constellation symbol and the phase offset are detected by using the spreading code estimated in the first step.Specifically,the spreading code can be estimated by
After obtaining ˆc,at the second stage,the information symbolxand the phase offsetζcan be estimated readily via
From (10) and (11),the search complexity of the LC detector is of order∼O(L+MP),which is lower than that of the ML detector.
Remark 1.Obviously,thesynchronizationbetween theAPandtheRISisrequiredforRIS-HPCM,which canbereadilyachievedbythefeedforwardlinkbetweenthem.InRIS-HPCM,theRISsimultaneously performsDSSSandpassivebeamformingonincident signals.Specifically,asseenfrom(8),thecomposite symbolxejζisspreadbythespreadingcodecover Lchips,andthechannelqualityissignificantlyenhanced.Therefore,RIS-HPCMcanachieveboththe spreadinggainandthebeamforminggain.Ontheotherhand,duetotheDSSS,RIS-HPCMresultsin signalswithawiderbandwidth,occupyingmorespectrum.Also,theRISneedstobeconfiguredLtimesper activesymbol,andthesamplingrateoftheanalogdigitalconverterattheusershouldbeLtimesthatin otherRIS-aidedcommunicationsystems.Thesemay increasetheenergyconsumptionandhardwarecosts.
III.PERFORMANCE ANALYSIS
In this section,we analyze the BER performance of RIS-HPCM by assuming the ML and LC detectors.Tight upper bounds on the BERs of the active and passive information are derived in closed-form.
3.1 Performance Analysis for the ML Detector
In order to derive the BER upper bounds for the ML detector,we first consider the pairwise error probability (PEP),Pr(x,c,ζ→),which is the probability for the event that the transmitted (x,c,ζ) is erroneously detected asTherefore,given the channel state informationh,the corresponding instantaneous PEP can be expressed as
After putting y in (8) into (12) and performing some simple algebraic operations,we have
whereG=We observe thatGis a Gaussian random variable with
Accordingly,we can express the instantaneous PEP as
With the moment generating function (MGF) approach,the unconditional PEP can be derived as
whereMA(t)is the MGF ofA.
Since |gi| and |fi| are independent Rician random variables,we have[28]
fork=1,2.Further,Ntends to be a large number in practice.According to the central limit theorem(CLT),can be well approximated as a Gaussian random variable,i.e.,where
Finally,according to the union bounding technique,the BERs of the active and passive information for RIS-HPCM with ML detection can be upper bounded by
respectively,whered(x→) denotes the number of erroneous bits whenxis detected as,andd(c,ζ→) is the number of erroneous bits when (c,ζ) is detected as
3.2 Performance Analysis for the LC Detector
In the LC detector,as shown in(10)and(11),we first obtain the estimate of c through correlation operations,and then detectxandζvia ML detection based on the estimate of c.According to the law of total probability,the BERs ofxand(c,ζ)for RIS-HPCM with the LC detection can be expressed as
respectively,wherePerepresents the erroneous spreading code detection probability,Pb1is the average bit error probability (ABEP) ofxin the case of correct estimation of the spreading code,Pb2is the ABEP of (c,ζ) in the case of correct estimation of the spreading code,and the factor 0.5 accounts for the ABEP in the case of incorrect estimation of the spreading code.
For the derivation ofPb1andPb2,the spreading code is detected correctly,i.e.,c=Hence,from (11),the instantaneous PEP for theMP-PSK constellation points can be expressed as
Similar to(16),we can obtain the unconditional PEP,from (24).The detailed procedures are omitted here to avoid redundancy.After obtainingthe upper bound onPb1can be given by
and the upper bound onPb2can be expressed as
Then,let us focus on the derivation ofPe.According to(10),the probability of detecting c as ˆc based onxandζis given by
whereX=|xejζhL+cHw|2andY=.Obviously,Yis an exponential random variable,whose CDF is given by
ForX,it can be expressed as
Hence,the MGF ofXis given by
In order to obtain the error probability of detecting the spreading code,letYι=,ι=1,...,L-1,where cιis theι-th spreading code with cι≠c.Therefore,the error probability of detecting the spreading code c conditioned onxandζcan be calculated by
Accordingly,the unconditional erroneous spreading code detection probabilityPecan be formulated as
Finally,by putting(33),(25),and(26)into(22)and(23),we arrive at the approximate BER expressions for the active and passive information for RIS-HPCM with the LC detector.
IV.SIMULATION RESULTS
In this section,we conduct Monte Carlo simulations to evaluate the BER performance of RIS-HPCM.The performance analysis in Section III is also verified.We explore the influence of system parameters,including the spreading factorL,the constellation sizeM,the size of the phase offset setP,and the number of reflecting elementsN,on the BER performance of RISHPCM.The performance comparison between RISHPCM and RIS-SM [10] is further presented.In all simulations,we plot the BER versus SNR that is defined as 1/N0.The Rician factor isK=1.Each BER point is obtained by averaging over at least 105channel realizations.
In Figure 3,we show the BER performance of RISHPCM with Walsh and Zadoff-Chu codes,where ML detection,L=8,andN=128 are employed for all schemes.BothM=P=2 andM=P=4 are considered.For clarity,the BER curves of the passive information forM=P=2 are not presented in Figure 3,since they are very close to those of the active information.As see from Figure 3,the RISHPCM schemes with Walsh and Zadoff-Chu codes almost achieve the same performance throughout the considered SNR region for bothM=P=2 andM=P=4.For this reason,Walsh codes are adopted in the remaining simulations unless otherwise noted.Also,as expected,we observe from Figure 3 that RISHPCM withM=P=4 performance worse than that withM=P=2,achieving a trade-off between SE and BER performance.
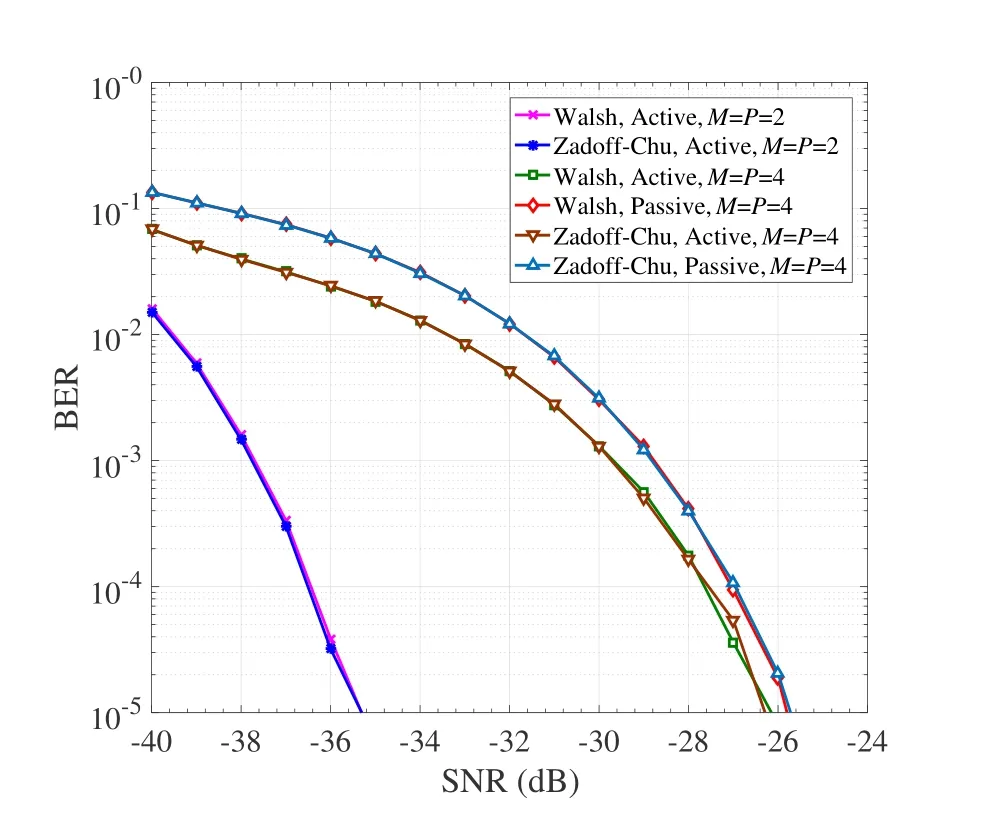
Figure 3.Performance comparison between Walsh and Zadoff-Chu codes for RIS-HPCM with ML detection,where M=P=2,4,L=8,and N=128.
In Figure 4,we compare the ML and LC detectors for RIS-HPCM,whereN=32,64,128,M=2,P=2,andL=8.Figures 4(a) and (b) present the BERs ofxand c &ζ,respectively.It can be seen from Figure 4 that for all consideredN,the LC detector achieves near-ML performance in terms of the BERs of bothxand c&ζthroughout the considered SNR region.This can be explained as follows.The first stage of the LC detector is able to achieve a comparable reliability to that of the ML detector.Once the spreading code is detected correctly,the second step of the LC detector becomes the ML detection.As expected,both the ML and LC detectors perform better with increasing the value ofN.At a BER value of 10-5,increasing the value ofNfrom 32 to 64 and from 64 to 128 leads to about 6.5 dB SNR gain for both detectors.In addition,we can see in Figures 4(a)and(b)that the gain obtained by doublingNis almost the same.
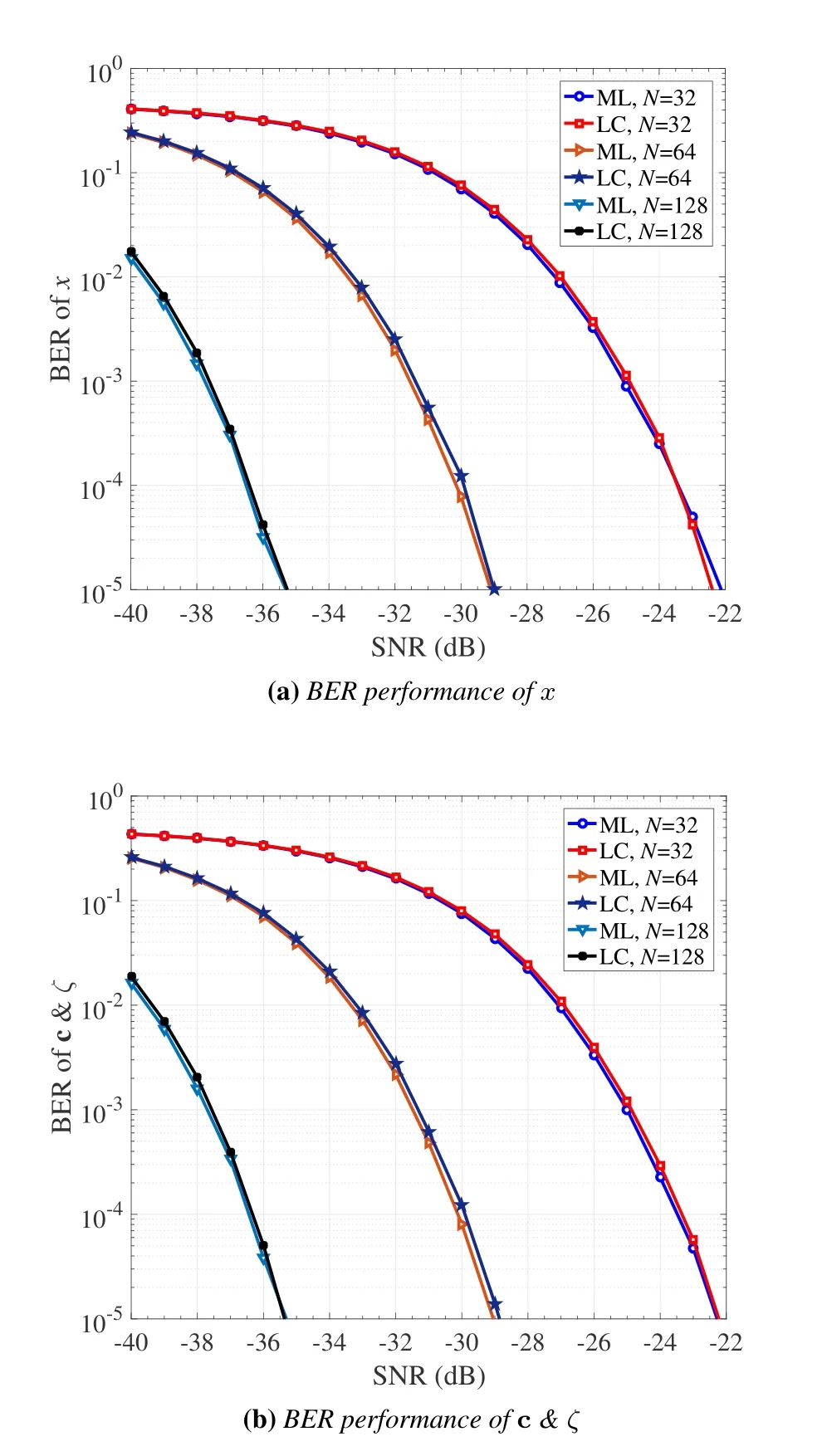
Figure 4.Performance comparison between the ML and LC detectors for RIS-HPCM:(a)BER of x and(b)BER of c&ζ,where N=32,64,128,M=2,P=2,and L=8.
Figure 5 shows the BER performance of RISHPCM with ML detection,whereN=64,M=2,P=2,andL=4,8,16.To verify the analysis in Section III.A,the upper bounds on the BERs of the active information(20)and the passive information(21)are also given in Figures 5(a)and(b),respectively.From Figure 5,we observe that all upper bounds match the simulated counterparts very well in the high SNR region.For fixed values ofN,M,andP,increasing the value ofLimproves the BER performance of bothxand c&ζdue to the increased spreading gain.Specifically,whenLincreases from 4 to 8 and from 8 to 16,about 2.5 dB SNR gain is achieved in terms of the BERs of both the active and passive information,at a BER value of 10-5.However,it is worth noting thatLcannot be increased infinitely,which is largely limited by the hardware implementation.
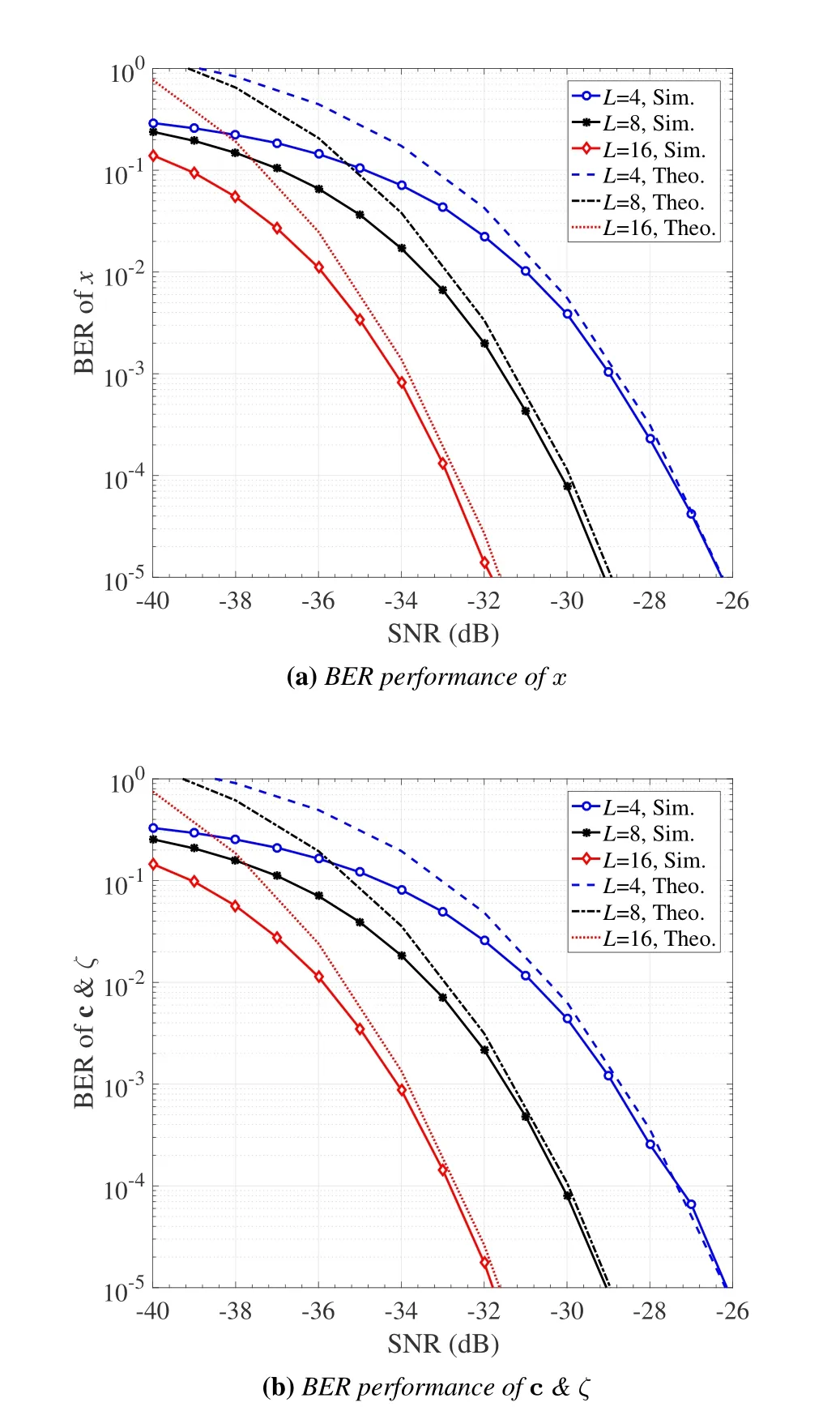
Figure 5.Performance of RIS-HPCM with ML detection:(a)BER of x and(b)BER of c&ζ,where N=64,M=2,P=2,and L=4,8,16.
Figure 6 presents the BER performance of RISHPCM with LC detection,whereN=128,M=2,P=2,4,8,andL=4.Figures 6(a)and(b)present the BERs ofxand c &ζ,respectively.To verify the analysis in Section III.B,the approximate BER expressions (22) and (23) are provided in Figures 6(a) and(b),respectively.As shown in Figure 6,the derived theoretical BER curves agree with the simulated counterparts in the high SNR region.For both the active and passive information,the BER performance deteriorates with increasing the value ofP.This can be explained as follows.Increasing the value ofPresults in a larger constellation size ofMP-PSK,and a smaller minimum Euclidean distance,which decreases the detection accuracy.Since theMP-PSK symbol carries both the active and partial passive information,the BERs of both the active and passive information become larger with increasing the value ofP.Therefore,for the selection ofP,we should comprehensively consider the detection performance and SE of the system.Specifically,about 4 dB SNR loss is incurred whenPincreases from 2 to 4 for the performance of both the active and passive information,while about 5 dB SNR loss occurs whenPincreases from 4 to 8,a BER value of 10-5.
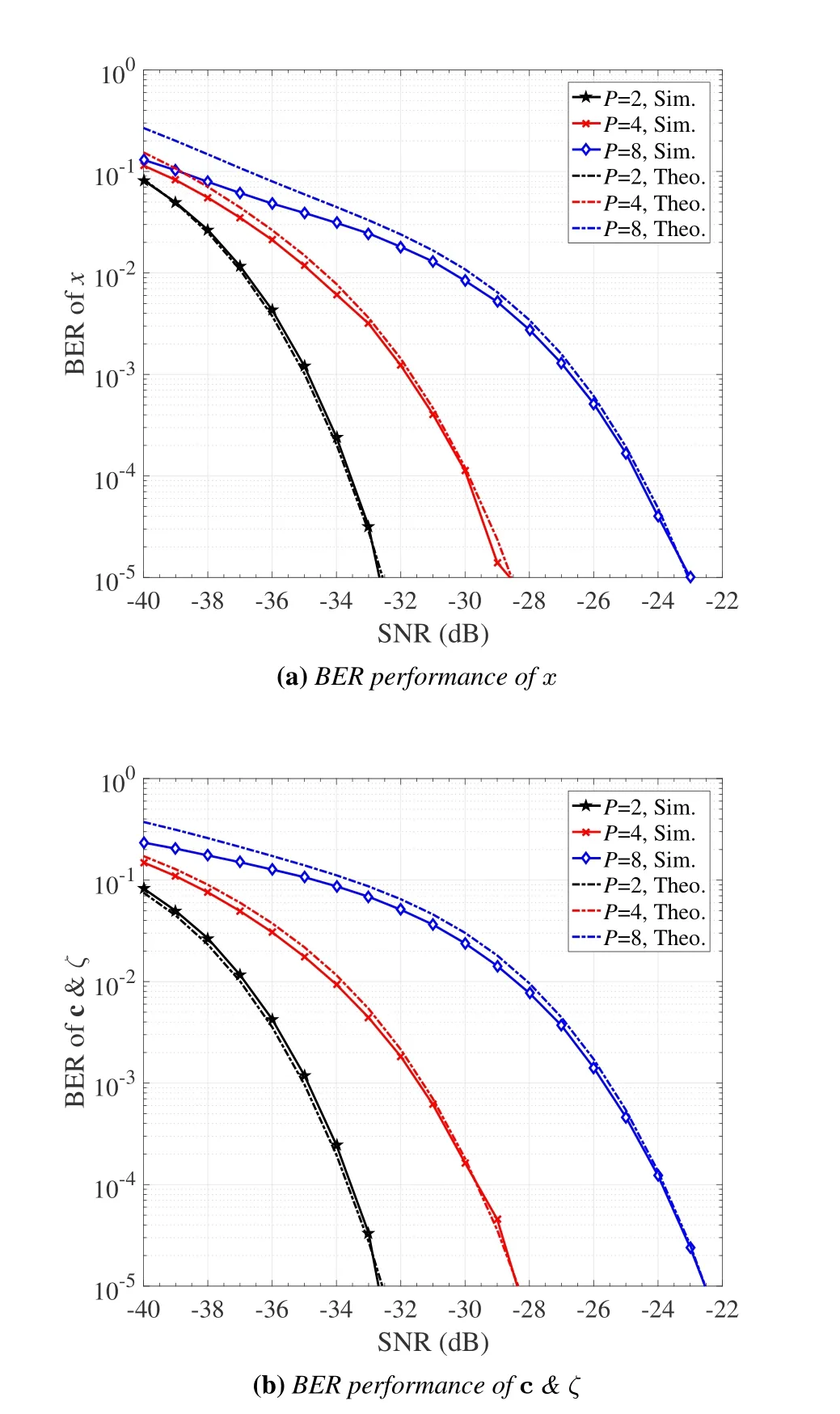
Figure 6.Performance of RIS-HPCM with LC detection:(a)BER of x and(b)BER of c&ζ,where N=128,M=2,P=2,4,8,and L=4.
Figure 7 depicts the BER performance of RISHPCM with ML detection,whereN=128,P=4,L=8,andM=2,4,8.It can be seen from Figure 7 that the BER performance of both the active and passive transmission deteriorates with increasing the value ofM.This is because a larger value ofMleads to worse performance ofMP-PSK demodulation,which impacts both the active and passive transmission.This is similar to the effect ofP.IncreasingMresults in worse BER performance while achieving the SE improvement of the active transmission.Specifically,increasingMfrom 2 to 4 results in about 5.5 dB SNR loss and 6 dB SNR loss for the active and passive transmission,respectively.Similarly,whenMis increased from 4 to 8,the SNR loss of active and passive information is about 5.5 dB and 6 dB,respectively.In addition,it can be found that when the modulation order increases,the performance gap between the BERs of the active and passive information increases.
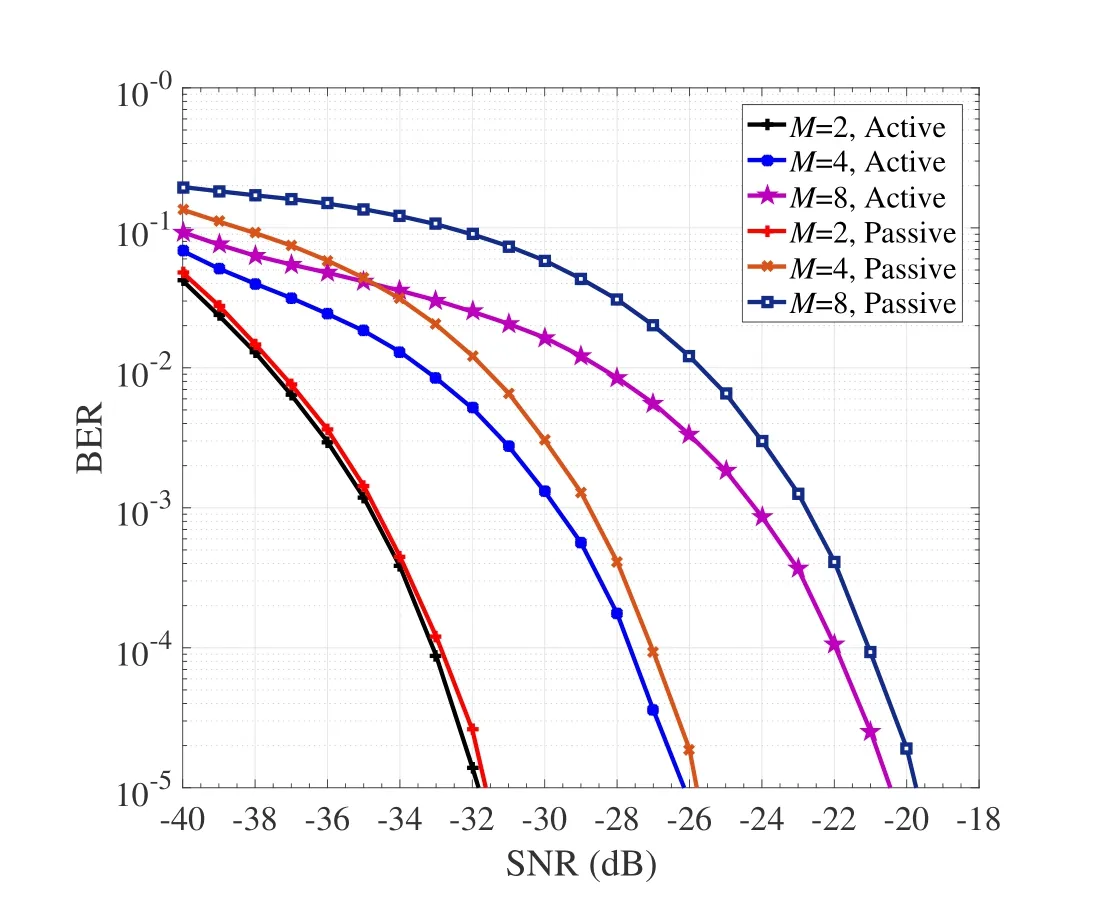
Figure 7.Performance of RIS-HPCM with ML detection,where N=128,P=4,L=8,and M=2,4,8.
Figure 8 shows the performance comparisons between RIS-SM [10] and RIS-HPCM at the same SE.Figure 8(a)shows the BER curves associated with ML detection,while Figure 8(b)plots the BER curves associated with LC detection.In RIS-SM,the index of the selected receive antenna conveys the passive information oflog2NRbits,whereNRis the number of receive antennas.RIS-SM usesM=4,NR=8,andN=128,while RIS-HPCM usesM=4,P=2,L=4,andN=128.RIS-SM and RIS-HPCM achieve the same SE of 2 bpcu for the active transmission and 3 bpcu for the passive transmission.Moreover,RIS-HPCM and RIS-SM employ the LC detector and the greedy detector (GD) in Figure 8(b),respectively.It should be noted that the GD detector is a LC and sub-optimal detector for RIS-SM.As shown in Figure 8(a),for the active transmission,RIS-SM obtains approximately 3 dB SNR gain at a BER value of 10-5over RIS-HPCM;for the passive transmission,RIS-HPCM obtains approximately 9 dB SNR gain at a BER value of 10-5over RIS-SM.Hence,for ML detection,the superiority of RIS-HPCM over RIS-SM lies in the passive transmission.Interestingly,as shown in Figure 8(b),the performance comparisons with LC detection are different from those with ML detection,and with LC detection,RIS-HPCM performs better than RIS-SM in terms of both active and passive transmission.Specifically,for active transmission,RIS-HPCM has a SNR gain of about 3 dB compared with RIS-SM at a BER value of 10-5,while for passive transmission,RIS-HPCM achieves a SNR gain of about 10 dB.
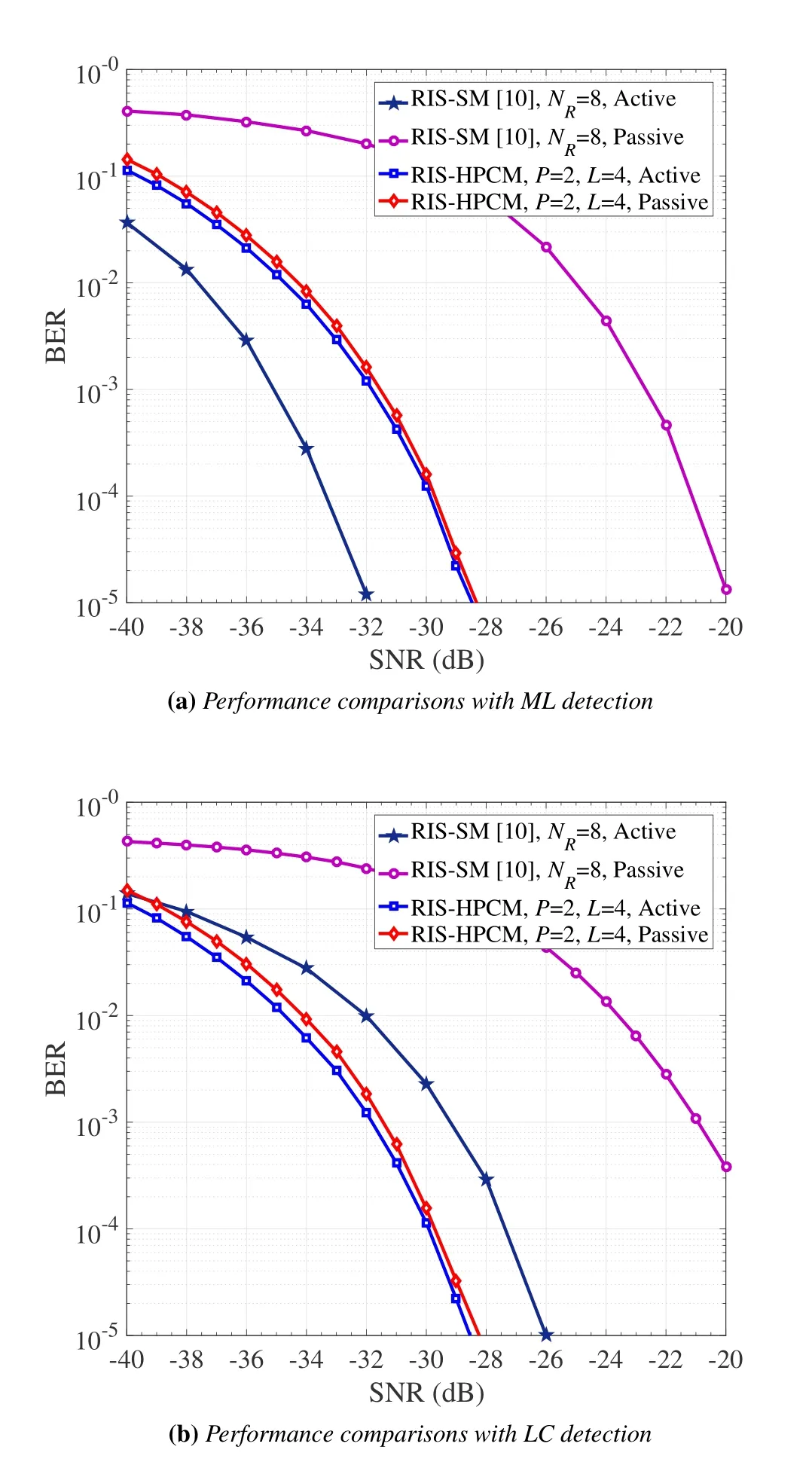
Figure 8.Performance comparisons between RIS-SM and RIS-HPCM.RIS-SM uses M=4,NR=8,and N=128,while RIS-HPCM uses M=4,P=2,L=4,and N=128.
V.CONCLUSION
In this paper,we have developed a hybrid RIS-based modulation,i.e.,RIS-HPCM,for SR.In RIS-HPCM,the RIS performs passive beamforming to implement DSSS on the incident signal and employs the spreading codes and phase offsets to convey its own information.A LC detector has been designed for RISHPCM.Upper bounds and approximate mathematical expressions for the BERs of ML and LC detectors have been derived in closed-form.Finally,the BER performance of RIS-HPCM has been simulated extensively,whose results have shown that RIS-HPCM significantly outperforms RIS-SM when LC detector is used.We remark that,RIS-HPCM can be further extended to multi-user scenarios with deep learning[29].
ACKNOWLEDGEMENT
This work was supported in part by the National Natural Science Foundation of China under Grant 62201228 and Grant 62001190,and in part by the Science and Technology Major Project of Tibetan Autonomous Region of China under Grant No.XZ202201ZD0006G02.
杂志排行
China Communications的其它文章
- Learning-Based Dynamic Connectivity Maintenance for UAV-Assisted D2D Multicast Communication
- AIGC Scenario Analysis and Research on Technology Roadmap of Internet Industry Application
- Dynamic Visible Light Positioning Based on Enhanced Visual Target Tracking
- Ultra Dense Satellite-Enabled 6G Networks: Resource Optimization and Interference Management
- Analysis and Optimization of Validation Procedure in Blockchain-Enhanced Wireless Resource Sharing and Transactions
- Anti-Jamming and Anti-Eavesdropping in A2G Communication System with Jittering UAV
