数列及函数极限的几种特殊求法①
2023-11-05赵士元
赵士元
(朔州师范高等专科学校数计系,山西 朔州 036000)
0 引 言
极限概念是高等数学中最抽象的基础概念,从连续到导数、从微积分到级数等都是用极限来定义的,是高等数学学习的第一个难关,贯穿了高等数学的始终。求极限的方法有很多,比如:利用单调有界定理、两边夹定理、中值定理、定积分定义、等价替换、洛必达法则、无穷小量的性质、泰勒公式等方法。因此,全面掌握极限概念与求极限的方法及技巧对学好高等数学有一定的指导意义。
1 利用单调有界定理求证数列极限[1]
若数列{an}单调增加(或单调减少),且有上(下)界,则数列{an}收敛。
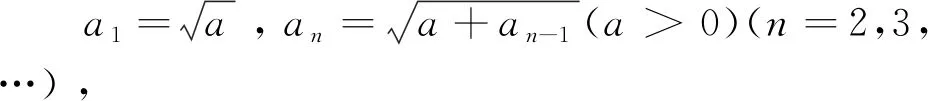

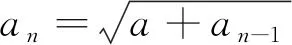
又因为an+1-an与an-an-1同号,而

即a2>a1, 所以an+1-an>0.即{an}为单调递增数列。
显然
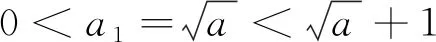
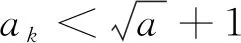
当n=k+1时,有

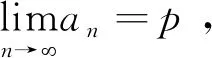
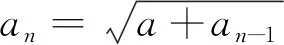
故p2-p-a=0
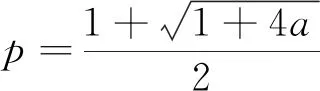
2 利用定积分定义求数列极限
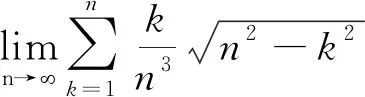
解
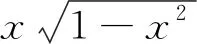
3 利用裂项法求数列极限
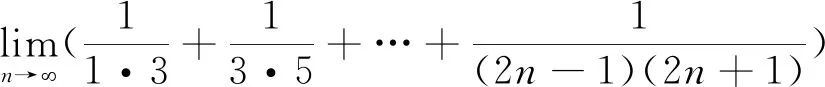
解:由于
所以
4 利用两边夹定理求极限
(1) 设有三个数列{an},{bn},{cn},若∃N∈N,∀n>N,有an≤bn≤cn,且
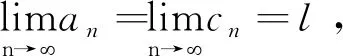
例4[2]求
解:
由于
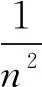
所以
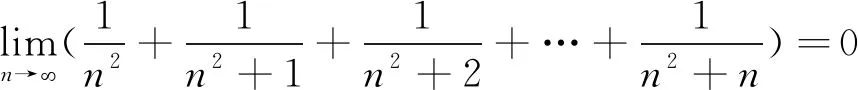
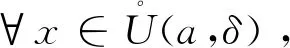
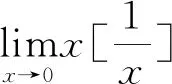
解: 因为
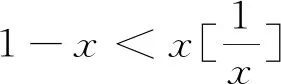
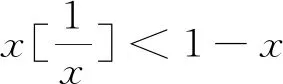
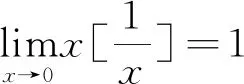
5 利用消去零因子法求函数极限
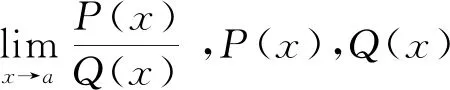
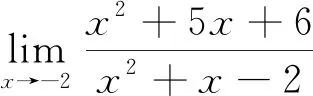
解:
6 利用重要极限求函数极限[2]
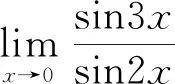
解:
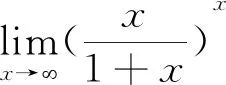
解:
7 利用无穷小量的性质巧求极限[3]
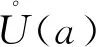
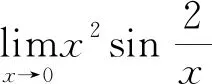
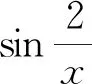
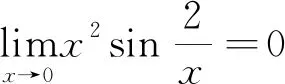
8 利用洛必达法则求极限[4]

若函数f(x)与g(x)满足下列条件
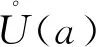
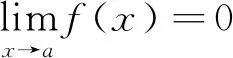
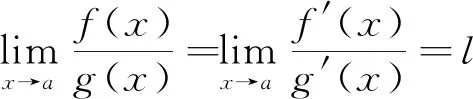
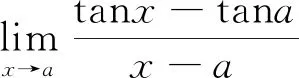
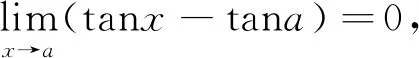
根据洛必达法则,有

若函数f(x)与g(x)满足下列条件:
(1)在(a,+∞)可导,且g′(x)≠0;
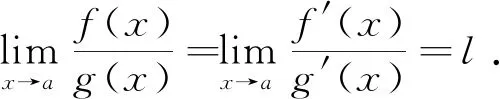
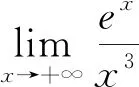
解:

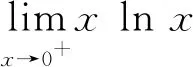
9 利用等价替换求函数极限
最常用的等价替换[1]有:
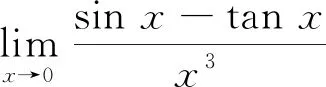
解:
10 利用中值定理求函数极限[4]
对于一些含有积分式子或分式的极限,可考虑利用积分中值定理或微分中值定理进行求解
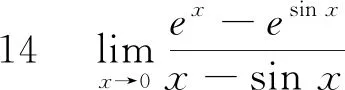
解:设f(x)=ex,由微分中值定理得:
ex-esin x=(x-sinx)e[sin x+θ(x-sin x)][cosx+
θ(1-cosx)]
从而,
11 利用泰勒公式求函数极限
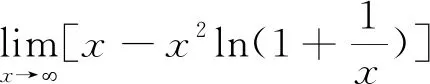
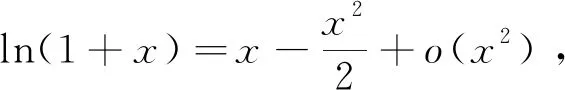
12 结 论
由于高等数学中极限部分内容多、课时短、知识点抽象,对于学生学习动力不足、大学授课方法有别于中学等情况,困惑、厌烦焦虑等情绪比比皆是,这对后期内容的教授,带来了更大的挑战。数列及函数极限概念是高等数学中一个非常重要的基本概念, 是学习变量数学的必备工具, 涉及到很多方面的知识,甚至贯穿于整个高等数学知识体系,所以在求极限时,首先要充分考虑, 分析所求函数的类型, 然后再去确定用什么方法,求极限的题型灵活多变,所以一定要熟练掌握求极限的方法,准确掌握求极限的基本方法有利于更好地学习高等数学。
