一种2R1T并联机构位置反解和工作空间分析①

张金萍, 何学军,2, 郭朋浩,2, 李宪芝, 罗厚学

(1.沈阳化工大学机械与动力工程学院,辽宁 沈阳 110142;2.营口理工学院机械与动力工程学院,辽宁 营口115014;3.营口理工学院化学与环境工程学院,辽宁 营口 115014)

0 引 言

多链构型的并联机构,具有优异的位置精度和强大的负载能力。这种机构的应用非常广泛。例如,它可以被用于工业生产线上[1],执行复杂的装配操作,从而减少人工干预。此外,它还可以用于医疗[2]、安保[3]、军事[4]和物流[5]等领域。当前,尽管存在一定的并联机构构型研究成果,但机构的性能指标还需进一步提升。因此,新型的少自由度并联机器人被设计出来,运用螺旋理论分析结构并用改进的G-K公式求解机构的自由度,分析其构型设计,并提高并联机器人的性能指标。通过数值搜索法,展开并联机构的工作空间分析[6],并优化并联机构的性能指标。设计了一种带封闭支链的2R1T并联机构,并对该机构进行了自由度分析、运动学的反解求解及工作空间分析。

1 机构自由度分析

1.1 机构组成

2R1T并联机构由定平台和动平台加三条支链组成。定平台和动平台都是等边三角形,边长各为2a,2b。两个平台之间通过三个不相同的支链相连接,包括两个结构相同的RPS支链A1B1,A2B2和一个长度为r的SS支链A3B3。旋转副R1,R2的轴线方向分别与A1A2垂直,而R3的轴线方向则与A1A2平行。此外,在A3B3的四分之三处,有一个由R3P3S5组成的支链通过R3,S5分别与A3B3,A1A2相连接,且S5位于A1A2的中点处。如图1所示。

图1 2R1T机构简图

1.2 自由度分析

支链1的运动螺旋为:

其反螺旋为式(1):

(1)

支链2的运动螺旋为:

其反螺旋为式(2):

(2)

支链3包括闭环支链(S4+ S5P3R3)和S3,

闭环支链(S4+ S5P3R3)分析:

S4运动螺旋为:

其反螺旋为式(3):

(3)

S5P3R3运动螺旋为:

其反螺旋为式(4):

(4)

(3),(4)反螺旋为:

S3的运动螺旋为:

所以,支链3的运动螺旋为:

支链3的反螺旋为式(5):

(5)

对式(1),(2),(5)求反螺旋,得动平台运动螺旋系为式(6):

(6)

动平台有1个绕x轴轴线的旋转自由度,1个绕y'(过B1,B2平行y轴)轴轴线的旋转的自由度,及1个沿着y轴方向的移动自由度。

采用修正的Grubler-Kutzbach(G-K)公式计算自由度,即式(7):

(7)

式(7)中:M为机构的自由度;d为机构的阶数,d=6-λ,λ为公共约束;n为连杆数目;g为运动副的数目;fi为第i个运动副的自由度;v为冗余约束;ζ为局部自由度。

由动平台所受约束可知,机构不存在公共约束,λ=0;无冗余约束,v=0;无局部自由度,ζ=0。应用修正G-K公式可得:

M=6×(9-11-1)+21=3

由计算结果可知,该并联机构自由度为3,与螺旋理论分析结果一致。

2 运动学分析

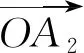
所以,

由1.1部分可知,机构有绕着新的x轴和y轴的转动以及沿x轴的移动共三个自由度,假设动平台以欧拉角的形式进行运动,先绕x轴旋转α角度,再绕y轴旋转β角度,最后沿x轴平移s毫米。

(8)

其中,

(9)

设移动副P1,P2,P3的位移距离分别为d1,d2,d3:

(10)

3 2RT1并联机构工作空间分析

根据运动学分析得到的位置反解表达式,采用数值搜索算法的方式在Matlab软件中计算2R1T并联机构的三维工作空间表示,工作空间三维坐标及XY平面投影图如图3和图4所示。

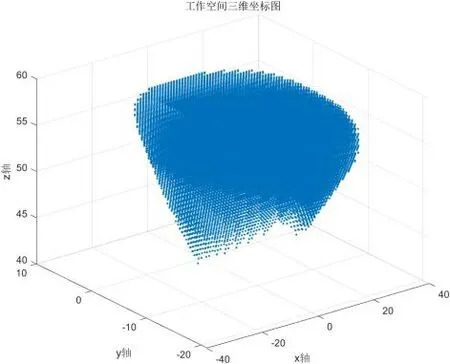
图3 工作空间三维坐标图

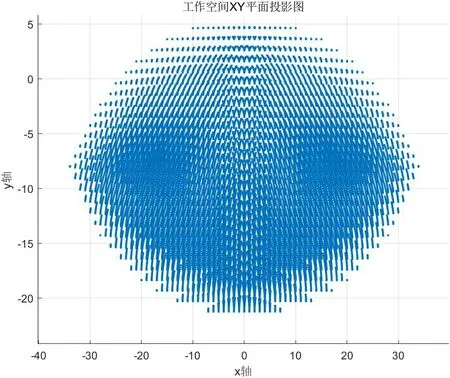
图4 工作空间XY平面投影图

从图3,图4中可以看出,2R1T并联机构工作空间形状规则,分布均匀,没有出现空洞的现象,说明并联机构运动性能及稳定性好。

4 结 语

文章中设计了一种2R1T并联机构,运用螺旋理论分析机构自由度,并用改进的G-K公式求解机构的自由度进行验证。对该并联机构的位置反解进行求解,得到了原动件的准确位移。同时,还采用数值搜索法对机构的工作空间进行了全面分析,得到了该机构精确而完整的工作空间。