基于Petri网的运输流程系统建模优化①
2023-11-05邢金库
孙 霞, 邢金库
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
0 引 言
目前,在我们的日常生活中,货物运输已经成为了不可或缺的一部分。在搬家或者运输货物时,我们都会使用到运输车辆,因此货拉拉近几年开始流行起来,越来越多的司机开始进入到“货拉拉”公司,截止至2022年8月,“货拉拉”业务范围已覆盖352座中国内地城市,月活司机达66万,月活用户达950万[1]。“货拉拉”通过共享模式整合社会运力资源,完成海量运力储备,并依托移动互联、大数据和人工智能技术,搭建“方便、科技、可靠”的货运平台,实现多种车型的即时智能调度,为个人、商户及企业提供高效的物流解决方案[2]。可是由于货拉拉在运输过程中货物破损等问题经常引起纠纷,给客户带来不好的体验。Petri网是一种分布式系统的建模和分析工具,其业务流程模型可以应用于多种场景[3]。针对此类问题,通过Petri网对其建模进行了优化,将根据所运输物品分为易燃易爆类、易碎类、普通物品三类,根据类别的不同选择装载和运输的方式,有效的避免了在运输过程中易燃易爆类物品发生爆炸的危险情况的发生,同时也降低了易碎物体破碎的概率[4]。根据货物破碎后的处理情况,做出了相应的优化措施,客户和司机可以选择自行解决的方式,进行当面的协商。如果协商未果,可以选择平台接入,平台会根据情况快速处理,给出一个合理的解决方案。
1 基本概念
1)对于三元组N=(S;T;F)来说,只要满足三个条件就可以称为有向网,简称网。
1.S∪T≠∅∧S∩T≠∅.
2.F⊆T×S∪S×T.
3.dom(F)∪cod(F)=S∪T
(1)
S为库所,T为变迁,皆为Petri网的集合,且两个集合中无任何公共元,并且至少一个不为空集,F为流关系,三元组(S;T;F)中的分号表明了F对S和T的从属性:T和S是相对独立的,且用S和T来定义F。
2)六元组Σ=(S;T;F;K;W;M0)是一个Petri网系统,又被简称为网系统,其中N=(S;T;F)是有向网,被称为Σ的基网。W是N上面的权函数,表示资源消耗或产生的量,K是指容量函数,M0是初始状态标识。M是N=(S;T;F)上的标识,且t∈T。其中t在M中具备有发生权的条件为∀s∈.t:M(s)≥W(s,t)∧∀s∈t.:M(s)+W(t,s)≤K(s),且记作M[t>.[5]。当t在M有发生权了以后,M变为M′,由式(2)得出:
(2)
3)Petri网的发生关系。Petri网的发生关系包括以下几种:顺序关系、并发关系、冲突关系、冲撞关系等。事件e1,e2∈E在情态c发生顺序关系的条件为:c[e1>c′∧c′[e2>┐∧c[e2>,即两个事件e1和e2的发生具有先后之分,后者发生的条件是前者发生。并发关系发生的一个条件为两个事件e1和e2相互独立,即(.e1∪e1.)∩(.e2∪e2.)=∅∧c[e1>∧c[e2>.并发事件e1,e2可以同时发生。
2 传统的“货拉拉”运输流程模型
在运输货物的流程中经常发生用车调度不方便和货物破损等问题,针对这些问题,通过Petri网对其运输流程的原始模型进行优化,实现更加高效的运输,也保证了运输过程的安全可靠[7]。
图1为传统货拉拉运输流程的模型,首先用户需要点击货拉拉app,输入出发地和目的地,并且根据所需运送货物的量来选择使用的车型,此时T0,T1,T2发生,它们三个之间变迁是严格序关系,即T0,T1,T2依次发生,也就是后一个发生的前提是上一个变迁发生。接下来用户通过运输的货物量来选择车型,如果货物重量在500公斤以内,可以选择小面包车,此时变迁T3和T4发生;货物重量在1 t以内选择中面包车,此时变迁T5和T6发生;货物重量在1~1.5 t选择小货车,此时变迁T7和T8发生;货物重量在1.5~1.8 t选择中货车,此时变迁T9和T10发生。用户会在四种车型中悬着出做合适的一种,即变迁T3,T5,T7,T9之间是排他关系,只能有一种情况发生。用户选择完车型开始发布订单,此时变迁T11发生,车主们进行抢单,如果有司机抢到订单,则变迁T12发生,车主出发到用户所在地;如果没有车主接单,此时变迁T13发生,没有司机接单,则会返回到变迁T11,再次在平台发布订单,供车主及时抢单,此时T12和T13是排他序关系。待车主接单后,将车开到出发地点,变迁T14发生,开始对货物进行验货,用户和车主共同确认过后开始装车,T15发生,待车到达了目的地,用户确认订单并付钱,完成订单。变迁T15,T16,T17,T18是顺序关系,依次发生,他们之间满足严格的序关系,记做T15→T16→T17→T18.

图1 传统货拉拉运输流程的模型流程图
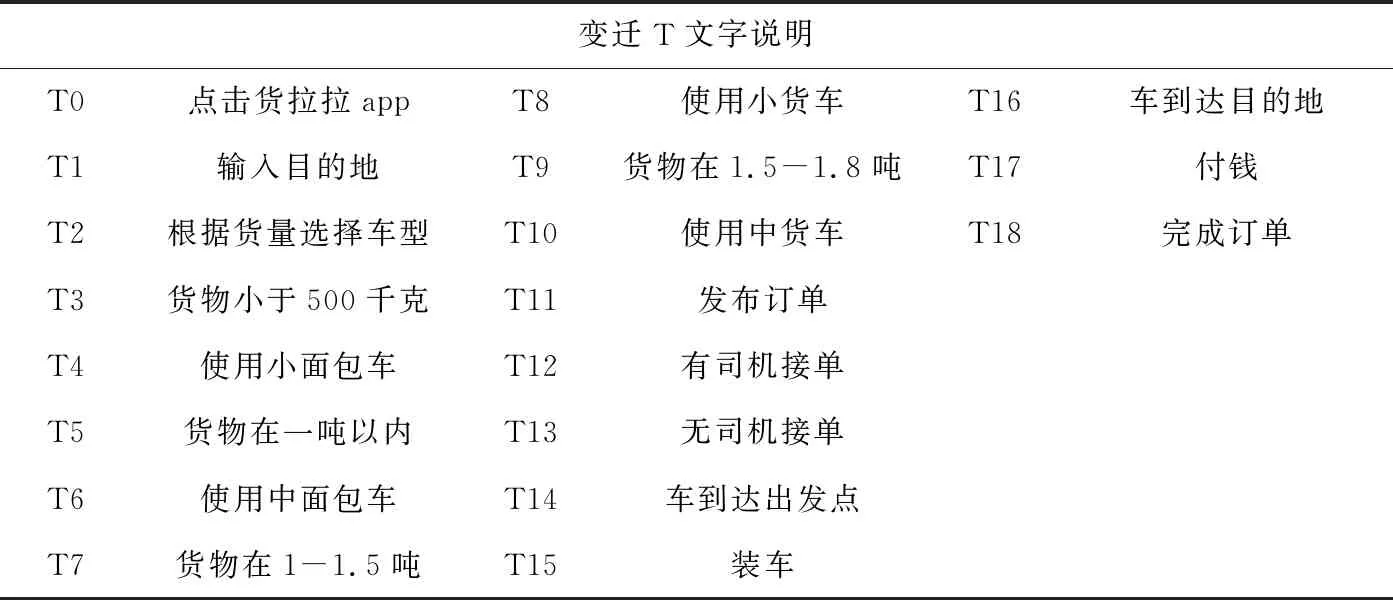
表1 传统的“货拉拉”运输流程模型图各变迁符号及其意义文字说明
3 优化后的“货拉拉”运输流程模型
货拉拉在传统的运输过程中,没有将货物进行分类别的装车运输,导致产生一些不必要的问题。而且对于订单出现异常时的纠纷问题不能很好的进行解决,可以利用Petri网的相关运行规则,通过增加相应的控制结构对其传统的模型进行优化[8]。图2为系统优化后的模型,主要是对货物的运输分类和对异常订单处理的优化,当装车前的验货工作完成时,即变迁T15发生后,根据物品的种类分为三类,易燃易爆品应使用正规的危险品运输车运输,禁止装车,该过程变迁T16,T17,T18依次发生,为顺序关系,记作T16→T17→T18,易碎物品应采用特定的包装并将物品装在易碎品区域小心装车,此过程T19,T20发生,普通物品则正常装车即可。其中变迁T16,T17,T18为排他关系,变迁T20,T21为并发关系,可以共同发生。当车辆到达目的后,进行验货,如果货物无问题,没有丢失或破损,用户便付款,完成订单,交易结束。此过程中变迁T24,T25,T26为顺序关系,依次发生。如果货物有问题,发生了破损或者丢失的现象,则用户与车主可以采用自行解决的方法,赔款或者其他方式,变迁T28发生,如果可以自行解决,赔偿双方都可以接受,则问题处理完成,即变迁T31发生,则返回到变迁T25,根据所谈的价格进行付款。若自行解决未果,则平台出面解决,用户可以在平台投诉,平台处理异常单,最终给出一个令人满意的解决方案。其中变迁T29,T30为排他关系,只能有一个发生,待平台处理完成后再次返回到变迁T25,用户根据平台所给出的解决法案进行付款,最终订单完成,结束交易。通过增加的以上控制结构,在最大程度上保证了用户和车主共同的利益,使得用户的满意度得到提高。
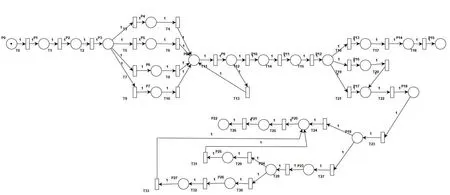
图2 优化后的“货拉拉”运输流程模型流程图
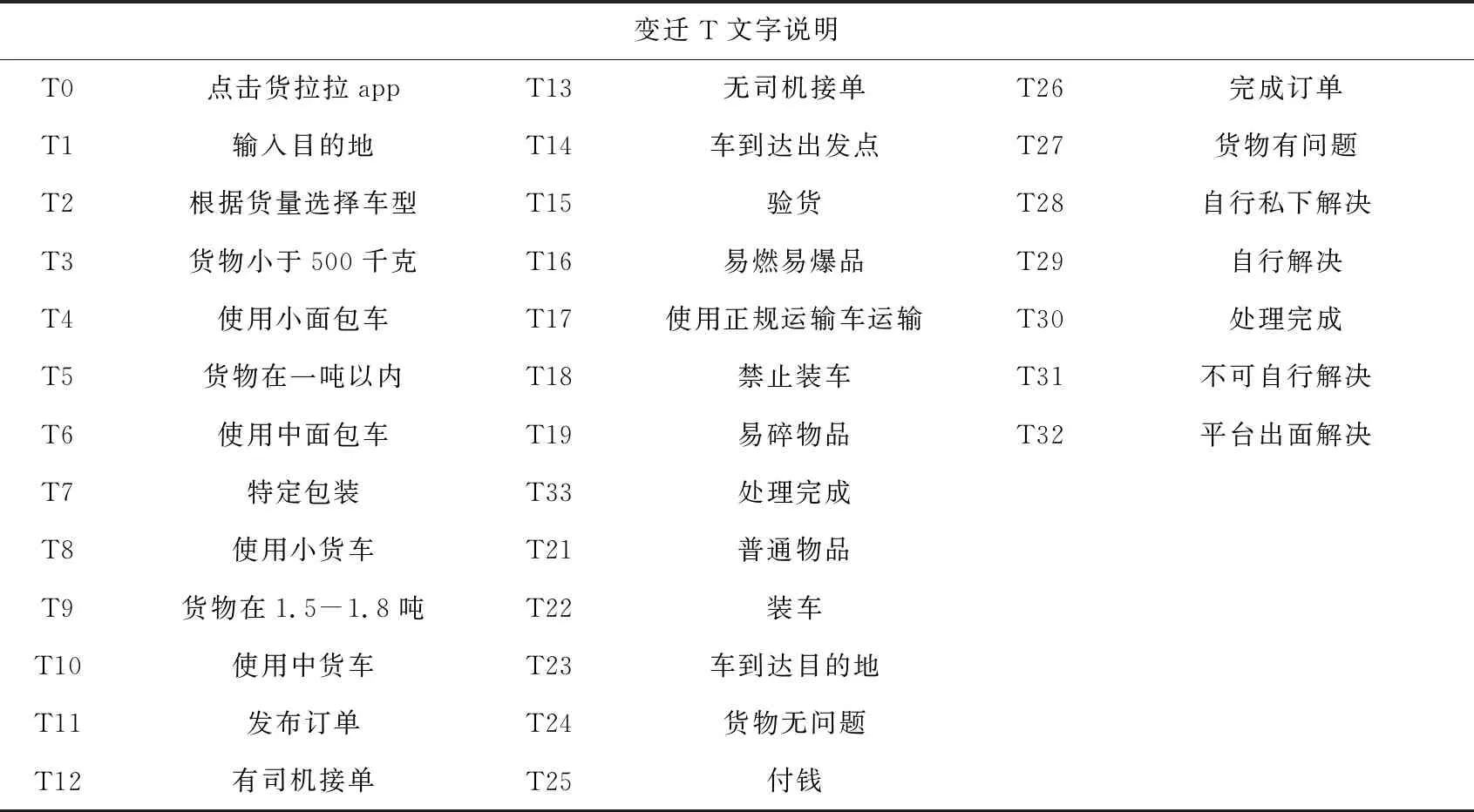
表2 优化后“货拉拉”运输流程模型图各变迁符号及其意义文字说明
优化后的货物运输模型通过增加控制结构,实现了货物按类别分类运输和运输中发生问题后的订单异常处理的优化[9],不但可以减少货物运输中问题的出现率,同时也能在问题出现后及时有效的处理掉,使得货物的运输更加高效,也能够在最大程度上保证双方的利益,达到双赢的效果。图中各变迁符号及变迁文字说明见表2。
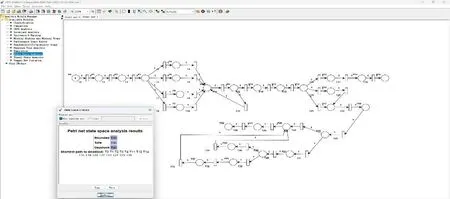
图3 优化后的Petri模型在PIPE软件中的仿真图
4 算法运用
在物流运输的过程中,不仅要考虑用户的利益,同时也要让车主的利益最大化,实现双赢的目的,蚁群优化算法已被广泛用于解决具有良好鲁棒性和正反馈的组合优化问题,在运输车辆运送的配车问题上,可以将蚁群优化算法加入其中,选择最优的配送路径以及距离最近的分配方式。
首先,可以将要分配的车辆作为蚂蚁访问的路径节点,代替原来的位置节点,根据用户下单用车事件对路径节点进行访问,其次,根据用户下单的时间和地点依据蚁群优化算法选择最优的派车方案。公式如下:
(3)
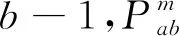
(4)
5 优化后的货拉拉运输流程Petri网性能的验证
5.1 优化后模型性能的分析
对优化后的模型进行性能分析,Petri网采用可视化图形描述,用形式化的数学方法支持,表达离散事件动态系统的静态结构和动态变化[10]。
通过对其静态性能进行分析,可以得出该模型是否稳定。货拉拉运输流程的Petri网的静态结构由三部分组成,即关联矩阵A、输入矩阵B、输出矩阵C,它们三者满足A=B-C.其关联矩阵如下图4所示:
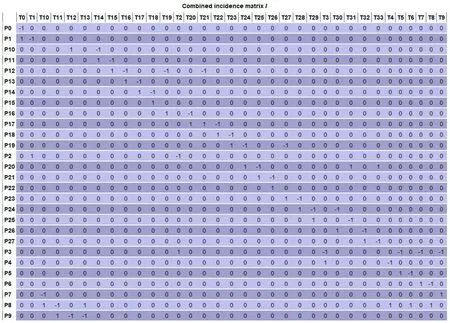
图4 关联矩阵
根据其关联矩阵,可以根据公式ATX=θT和AY=θS求出其通解X和Y,也就是S-不变量和T-不变量[11]。矩阵的通解为YT为:
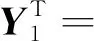
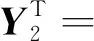
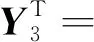
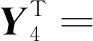
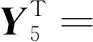
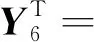
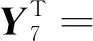
(5)
由式(5)通解可知整个过程中托肯总数不变,S-不变量能够反应托肯的流动路径,并且具有不变性,一直在整个过程中流动,因此该优化模型的Petri网的性能是稳定的、可行的[12]。
5.2 Petri网的性能的验证
为了验证运输流程Petri网的性能,看其是否具备正确性和可达性,将Petri网优化后的模型在软件PIPE中绘制,利用软件中的函数对模型进行验证[13]。运行结果如图5所示,可知构建的模型是可行的。
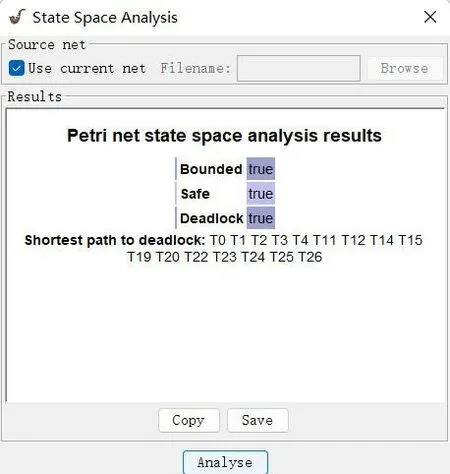
图5 PIPE仿真模拟结果图
6 结 语
为了处理传统运输过程中易发生危险事件和货物丢失或损坏等问题,通过在传统的运输流程中加入控制结构对传统的模型进行了优化,取得了以下成果:(1)解决了传统运输过程中易发生危险事件和货物丢失或损坏等问题,进而保证了运输流程的可靠性,提高了运输的效率,减小了运输中的危险性。(2)有效的解决了纠纷问题,将之前几天才能解决的问题在短时间内便可解决,提高了效率,用户的满意度得到了很大的提升。
随着运输流程的发展,也可将Petri网运用于重要医疗设施运输或重要危险物的运输中,结合Petri网性能的稳定性和可行性,使得未来的运输流程业务更加完善。
