“圆”题重现，赋能再出发

文／王晓华

我们遇到的综合题往往是在教材例习题的基础上，进行重新整合、变式或拓展而形成的。因此，我们要追“本”溯“源”，多角度思考，与所学的其他知识、思想方法串联起来，构建更为完整的知识结构。

【原题重现】（苏科版数学教材九年级上册第57 页例3）如图1，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，，BE分别交AD、AC于点F、G。判断△FAG的形状，并说明理由。

图1

【解析】根据圆周角定理的推论，得出∠BAC=90°。再将“弧相等”转化为∠ACB=∠ABE。根据三角形内角和定理以及垂直，得出∠ACB+∠DAC=90°，∠ABE+∠AGB=90°，故∠DAC=∠AGB，从而AF=FG。

【追问】点F为线段BG的中点吗？

【解析】因为∠BAC=90°，AD⊥BC，易得“子母型”这一基本图形，从而得∠BAF=∠ACB。又因为∠ACB=∠ABE，所 以∠BAF=∠ABE，从 而AF=BF。再由AF=FG，得BF=FG，故点F为线段BG的中点。

【点评】转化思想能够将复杂的问题简单化。我们要把曲线型问题（圆）转化为直线型问题，弧、弦、圆心角、圆周角之间往往也可以互相转化。因此，我们在审题的过程中就要巧妙地将条件进行转化。

【变式】若点E与点A在直径BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，请画出图形，再思考上题中的结论还成立吗？

【点评】同学们思考问题要全面。点A、点E可以在直径BC的同侧，也可以在异侧，由此得到图2。虽然图形发生了变化，但解题的方法是一致的。

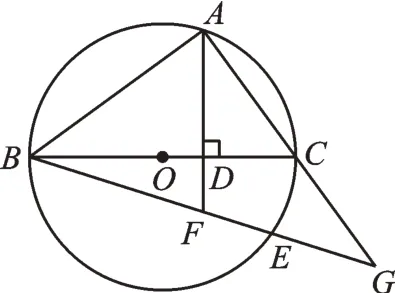
图2

【拓展1】在图1 的基础上，连接CE，探索BD、CD、CE三条线段之间的数量关系。

【解析】连接AE，如图3。根据，得到AB=AE。在CB的延长线上取一点C′，使得BC′=CE。连接AC′，根据圆内接四边形对角互补以及同角的补角相等，得出∠AEC=∠ABC′，从而△ACE≌△AC′B（SAS），得AC=AC′。又因为AD⊥BC，所以CD=C′D，进一步得到CD=BD+CE。当然，我们还可以继续思考，若在图2 的基础上连接CE，刚才的结论还成立吗？

图3

【点评】此题以圆为背景，把弧相等转化为弦相等，再一次变成我们熟悉的直线型几何问题。我们可以利用截长补短、全等三角形等相关知识加以解决。

由定性分析到定量计算，我们还可以赋予一些线段具体的长度值，从而产生新的问题。

【拓展2】如图1，若⊙O的半径为5，OD=3，求AF的长。

【解析】根据已知条件，得BD=2。连接AO，在Rt△ADO中，由勾股定理得出AD=4。由上面的分析，已得AF=BF，故求AF的长就是求BF的长。进一步把BF放在Rt△BDF中，设AF=x，则BF=AF=x，DF=4-x，再根据勾股定理，建立方程x2=22+（4-x）2，解得x=2.5。∴AF=2.5。

【点评】圆的综合性题目，除了证明外，还涉及计算。在求线段长度时，通常会根据勾股定理以及今后会学的相似、三角函数等知识加以解决。