数控多轴联动加工误差研究

李 可，王文超，熊亭超

（九江职业技术学院，江西 九江 332007）

制造业水平的高低是衡量一个国家工业科技实力的重要标尺，世界上的发达国家大多是制造业强国[1]。改革开放四十多年间，我国经济实力、科学技术水平都获得了大幅度提高，制造业也得到了深度发展。在早期阶段，我国的机械产品和机械加工设备，主要依靠从国外进口，德国、日本、美国都是我国制造业相关产品和设备的主要进口国。通过多年的学习和坚持自身的发展，我国具备了大多数民用机械产品和高端工业机械品的制造能力[2]。在机械加工设备方面，我国已经可以自行研发设计出多种类型的数控机床。尤其是多轴联动数控机床和数控加工中心的国产化，标志着我国机械加工和制造业技术水平得到了跨越式发展，步入了制造业强国的行列。在可喜的局面之下，也应该清醒地认识到我国制造产业尤其是机械加工技术领域中存在的不足[3]。对于多轴数控机床和数控加工中心，我国存在对加工误差分析水平不到位、加工误差无法得到全面补偿和修正、加工精度无法进一步提高的瓶颈问题。据此，本文以多轴联动数控加工误差为核心研究内容，以期为我国机械加工行业瓶颈问题的突破提供新思路。

1 多体理论及其拓扑结构

从国外研究的已有成果来看，对于多轴联动的数控机床进行误差分析，主要借助多体理论并结合齐次坐标变换。可见，多体理论是多轴联动数控加工误差分析的基础工具。多体理论的全称为多体系统运动学理论，即将多轴联动数控机床看成一个多体系统，通过运动学分析发现其加工误差的形成原因。运用多体理论进行多轴联动数控加工误差分析的主要流程如图1所示。

图1 运用多体理论进行多轴联动数控加工误差分析的主要流程

从图1 给出的流程框架可知，运用多体理论对多轴联动数控机床进行误差分析，可以对多轴联动数控机床的装配误差、运行误差、换刀误差和热误差进行分析，进而建立各类误差对应的数学模型，再采用齐次坐标计算，从而得到误差矩阵，进而将各项误差的矩阵进行合并，可以得到多轴联动数控机床的综合误差矩阵，最终实现对数控机床误差的准确表达。

所谓多体理论是将复杂系统看成多个物体组成的多体系统，本文要研究的多轴联动数控机床就属于复杂系统，因此满足进行多体系统抽象和多体理论分析的基础条件。多体理论既可以对闭环系统进行分析，也可以对开环系统进行分析。多轴联动数控机床属于开环系统，这就需要用到多体系统开环分析理论，其基础性工作是为其构建多体系统的拓扑结构。

因为多体系统涉及到多个个体，所以对于多轴联动数控机床的多体抽象，需要先将其进行个体分解，再对每一个个体形成编号，具体操作是先找到0 编号个体，然后按照各个体之间的关系依次进行编号，编号过程中要注意可能出现的分支情况，当机床内所有组成部分均配置标号后，多体系统正式建立。本文以XYZ型多轴联动数控机床为例，对其进行多体系统构建和编号处理，如图2 所示。

图2 XYZ 型多轴联动数控机床的多体抽象

从图2 中可以看出，在XYZ 三维坐标系下，多轴联动数控机床的各个组件被依次编号。其中，0 编号个体形成以后，又分别形成了2 个分支。左向分支包括了1 编号个体、2 编号个体，右向分支包括了3 编号个体、4 编号个体、5 编号个体。在这个拓扑结构之下，进一步进行关联关系、误差分析，可以分别依据各编号个体所在的位置有序展开。

2 多轴联动数控机床的运行误差建模

对于XYZ 型多轴联动数控机床而言，其加工误差的形成包括了多方面原因，如装配误差、运行误差、换刀误差和热误差等。其中，换刀误差、热误差属于局部误差，其对全局综合误差的影响占比较低，而装配误差在加工前就已经形成，在不能重复装配的情况下可以认定其为系统误差。所以，对机械加工过程中的误差影响最大的因素就是机床的运行误差。因此，这里主要对多轴联动的数控机床运行误差进行建模和分析。

XYZ 型多轴联动数控机床在运行过程中，其某一个自由度上的运动，总可以分解成X方向运动、Y方向运动、Z方向运动，要么是3 个方向上的运动效果合成，要么是2 个方向上的运动效果合成，要么是1 个方向上运动的对应。在这3 个方向上的实际运动，总会和预期的理想运动轨迹存在一定偏差，从而导致最终的停程位置也出现一定的偏差，这个位置上的偏差就是多轴联动数控机床的运行误差。

为了便于对多轴联动数控机床的运行误差进行建模处理，首先需要建立参考坐标系，具体过程为在多轴联动数控机床的床身上建立第一个坐标系，是为参考坐标系O。进而，对多轴联动数控机床的X方向溜板建立坐标系O1、对多轴联动数控机床的Y方向溜板建立坐标系O2、对多轴联动数控机床的Z方向溜板建立坐标系O3、对多轴联动数控机床的刀具建立坐标系M和对多轴联动数控机床的工件建立坐标系N。这些坐标系的三维坐标方向应一致，但各坐标系的原点互不重叠，从而可以实现各个坐标系的合理区分。

在上述的坐标系配置关系之下，可以得到多轴联动数控机床的运行误差矩阵

式中：e（x）为多轴联动数控机床X方向上的位移误差；e（y）为多轴联动数控机床Y方向上的位移误差；e（z）为多轴联动数控机床Z方向上的位移误差；t（x）为多轴联动数控机床X方向上的转动误差；t（y）为多轴联动数控机床Y方向上的转动误差；t（z）为多轴联动数控机床Z方向上的转动误差。

类似地，可以得到某一个个体坐标系下的运行误差矩阵，例如刀具坐标系下的运行误差矩阵

式中：em（）为多轴联动数控机床刀具X方向上的位移误差；em（）为多轴联动数控机床刀具Y方向上的位移误差；em（）为多轴联动数控机床刀具Z方向上的位移误差；tm（）为多轴联动数控机床刀具X方向上的转动误差；tm（）为多轴联动数控机床刀具Y方向上的转动误差；tm（）为多轴联动数控机床刀具Z方向上的转动误差。

3 多轴联动数控机床的加工误差分析

根据大量的数据分析和实际操作经验可知，多轴联动数控机床的运行误差形成与主轴振动、刀具磨损、3 个方向上溜板磨损有关，而不同原因形成的运行误差又会导致被加工工件不同形式的误差。下面分别从主轴振动、刀具磨损、3 个方向上溜板磨损这3 种情况出发，逐一分析其可能造成的加工误差。

首先，来看多轴联动数控机床主轴振动可能导致的加工误差，如图3 所示。

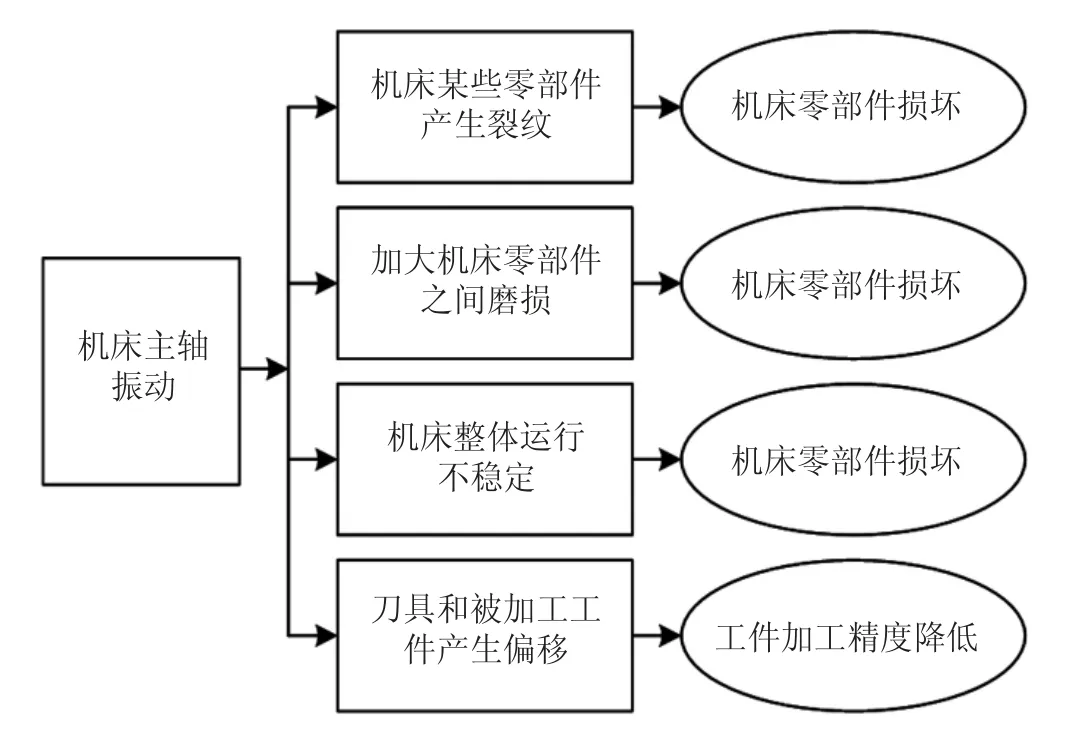
图3 多轴联动数控机床主轴振动可能导致的加工误差

从图3 中可以看出，多轴联动数控机床主轴振动，可能会形成4 个方向上的影响：第一个方向上，主轴振动可能会导致机床上某些零部件产生裂纹，最终后果是导致机床零部件损坏、机床被迫停机；第二个方向上，主轴振动可能会加大机床某些零部件之间的磨损，最终后果是导致机床零部件损坏、机床被迫停机；第三个方向上，主轴振动可能会导致机床整体运行不稳定，最终后果是导致机床零部件损坏、机床被迫停机；第四个方向上，主轴振动可能会导致刀具和被加工工件产生偏移，最终后果是导致被加工工件精度降低。可见，从加工误差的影响角度看，主轴振动第四个方向上的影响最直接。

其次，多轴联动数控机床刀具磨损可能导致的加工误差，如图4 所示。

图4 多轴联动数控机床刀具磨损可能导致的加工误差

从图4 中可以看出，多轴联动数控机床刀具磨损，可能会形成4 个方向上的影响：第一个方向上，刀具磨损可能会导致机床刀具后刀面出现磨损，最终后果是导致工件加工精度降低；第二个方向上，刀具磨损可能会导致机床刀具边界出现磨损，最终后果是导致工件加工精度降低；第三个方向上，刀具磨损可能会导致机床刀具前刀面出现磨损，最终后果是导致工件加工精度降低；第四个方向上，刀具磨损可能会导致刀具崩刃，最终后果是导致被加工工件精度降低。可见，刀具磨损在4 个方向上的影响，都会导致工件出现加工误差。

最后，多轴联动数控机床3 个方向上溜板磨损可能导致的加工误差，如图5 所示。

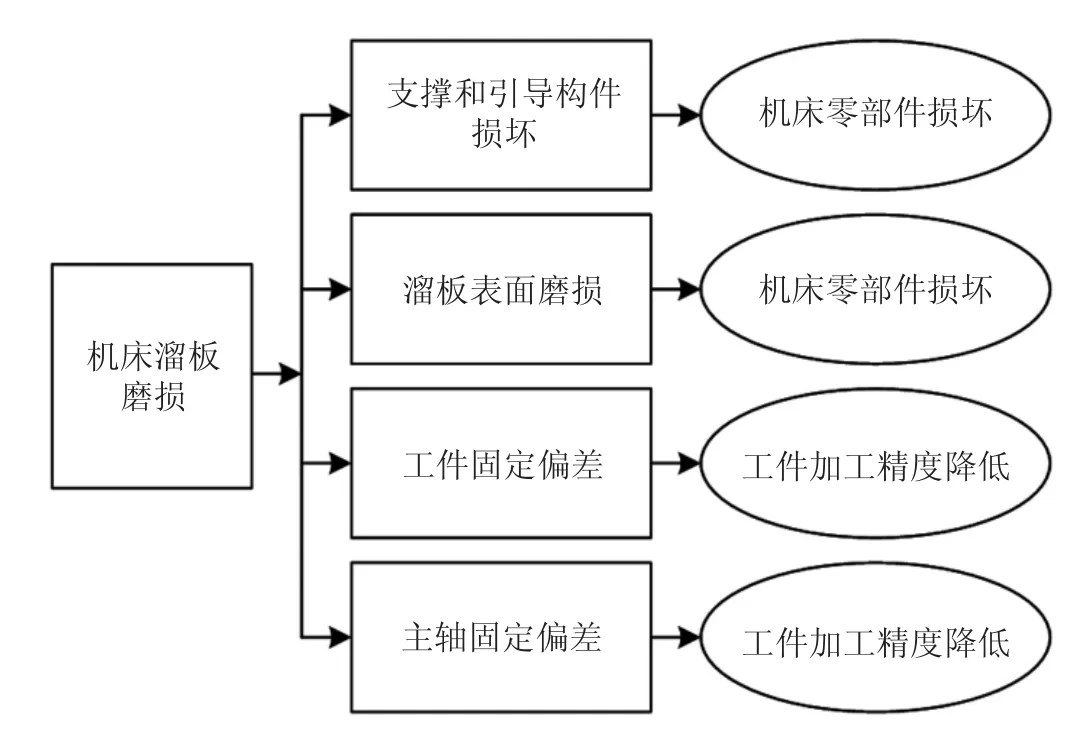
图5 多轴联动数控机床溜板磨损可能导致的加工误差

从图5 中可以看出，多轴联动数控机床溜板磨损，可能会形成4 个方向上的影响：第一个方向上，溜板磨损可能会导致支撑和引导构件损坏，最终后果是导致机床零部件损坏；第二个方向上，溜板磨损可能会导致溜板表面磨损，最终后果是导致机床零部件损坏；第三个方向上，溜板磨损可能会导致机械加工过程中工件固定出现偏差，最终后果是导致被加工工件精度降低；第四个方向上，溜板磨损可能会导致机械加工过程中主轴固定出现偏差，最终后果是导致被加工工件精度降低。可见，溜板磨损在后2 个方向上的影响，都会导致工件出现加工误差。

4 结论

多轴联动数控机床是目前机械加工最常用的工具，其加工精度直接关系到机械加工制造行业的产量和效率。本文对多轴联动数控机床进行误差分析，进而找到提升其加工精度的切入点。首先，以多体模型和多体理论，对XYZ 型多轴联动数控机床进行了多体拓扑结构划分和编号处理。其次，针对多轴联动数控机床中的运行误差进行了分析，建立了数学模型并给出了误差矩阵，明确了其中移动误差和转动误差在误差矩阵中的构成。最后，从主轴振动、刀具磨损、溜板磨损3 个方面，分析其可能导致的加工误差，进而定位了提升多轴联动数控加工精度的切入点。