基于TypeB 卡阅读器的数字解调算法

2023-11-05陈俊凝

科技创新与应用 2023年30期

陈俊凝

（西北大学信息科学与技术学院，西安 710127）

非接触式IC 卡系统由邻近卡（PICC）和近耦合设备（PCD）组成[1]，两者通过无线通信来完成信息传输。然而，PCD 解调误差大、速度慢，将出现系统无法正确通信的问题。解调能力提升，不仅可以发挥PICC 芯片性能优势，还能够提升自身的可靠性和安全性，这对系统的运行起到关键性作用[2]。

对于符合ISO/IEC 14443[3]TypeB 标准的PICC，其发送给PCD 的数字信息也是被附加在847 kHz 的副载波上的，再利用负载调制将双重载波发送给PCD，波特率为106 kbps。简而言之，就是通过106 kbps 的数字信号对847 kHz 的副载波信号进行二进制相移键控（BPSK）调制，根据协议规定，采用连续8 个周期初始相位固定的副载波信号来表示“0”，“1”则用与初始相位相差为连续8 个周期的副载波信号表示[4]。

1 BPSK 相干解调关键技术

BPSK 调制利用载波信号的相位信息调制，包络检波无法检测到相位变化，因此采用相干解调方式更为理想[5]。特别是在PICC 和PCD 进行信息交互时，由于信号较弱，再加上外界干扰，信号在传送过程中很容易产生偏差，导致本地振荡产生的相干载波不能严格实现同频同相，并且大大影响了解调性能，因此在接收端实现载波同步非常重要[6]。

本文对传统解调算法进行了深入研究，结合实际工程的需要，针对BPSK 相干解调过程中的载波同步、码元同步等关键技术进行研究与实现，并且提出了优化方案加以对比分析。

2 载波同步

2.1 传统Costas 环路原理

锁相环在调制解调中发挥着重要作用[7]，其是一种典型的反馈控制电路，能够锁定相位[8]。

然而传统锁相环技术对本地时钟频率要求较高，在跟踪载波时无法有效纠正较大频偏，也不适合宽率范围内的基带码元同步。

Costas 环[9]基于锁相环原理，其原理框图如图1所示。

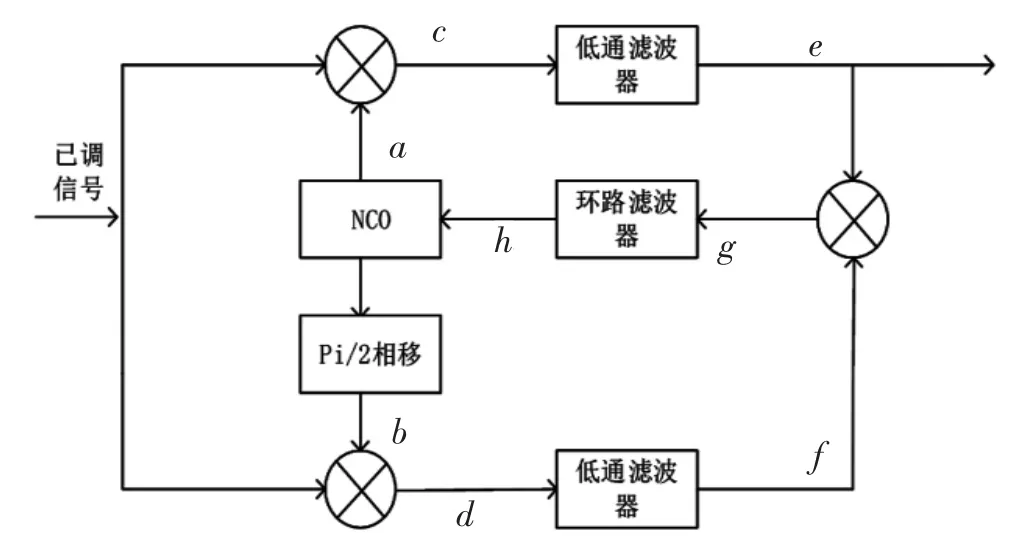
图1 Costas 同步环路原理框图

BPSK 信号被送入两路相乘器，与压控振荡器产生的a、b 两点电压相乘，得到c、d 两点电压，分别经过低通滤波器后相乘得到环路滤波器的输入电压vg为

式中：m（t）为调制信号，φ-θ 为本地信号与载波信号的相位差。对于BPSK 信号而言，m（t）=±1，并且在φ-θ 很小时，sin（φ-θ）=φ-θ，那么式（1）便可改写为

这时vg通过环路滤波器间接控制数控振荡器的频率，环路滤波器的作用就是低通，仅允许vg中的直流分量通过，数控振荡器（NCO）受到电压控制后调整频率不断使φ-θ 尽可能变小，直到它减小为0 时，就可以得到vg=1/2m（t）。

此时的电压和需要解调出的信号m（t）只是幅值不同，直接输出这个电压就可以得到近似的解调结果。

2.2 基于希尔伯特鉴相的解调算法原理

传统的Costas[10]环解调效果较为理想，不过其仍然存在某些缺点，载波频率高的时候，对滤波器特性要求也就变高，因此在实际应用中，常搭配叉积鉴频算法[11]来提高效率，实现起来会有些繁琐。本文在Costas 环法上做了部分改进，改进的结构如图2 所示。

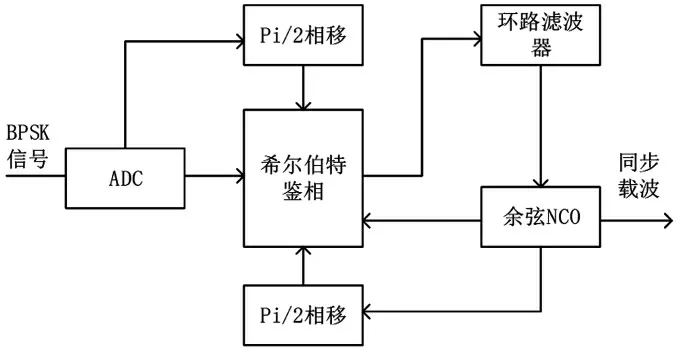
图2 基于希尔伯特鉴相的解调原理框图

希尔伯特鉴相模块总共有四路输入信号，与模数转换器（ADC）采样后的已调波和控制余弦NCO 产生的的信号有关，其中已调信号与其90°相移的信号固定不变，NCO 经过环路不断调整生成的余弦波和90°相移后的正弦波持续进入鉴相模块，这些信号在模块内部按照算法进行数学运算，得到相位差。计算过程如下。

设m为接收端收到的BPSK 调制信号，mh是调制信号移相90°后的信号，α 是余弦NCO 信号，β 是α 经过90°相移的信号，ωc是载波中心频率，△ω 为频偏，θ是载波的相位差，即

因此可以得到

运算结果便是本地载波与调制信号的相位差。

3 位同步

Gardner 算法[12]利用反馈环路，使得这种算法收敛速率高，运算量更小，所以本文选用了Gardner 定时同步环路实现码元同步，其原理框图如图3 所示。

图3 Gardner 算法原理框图

传统Gardner 定时环路通常在每个码元内的采样点数较少，不能根据初始赋值来直接锁定最佳抽样时刻，必须通过内插滤波器和NCO 模块不断地反馈计算出最佳采样点。对于本文所设置的参数，采样频率明显超过了码元速率，可以在每个码元内取得31 个采样点，在这些采样点中，有位于最佳采样时刻附近的值。

4 硬件实现

4.1 载波同步的硬件实现

载波同步模块采用Costas 同步环路由环路滤波器、NCO 以及希尔伯特鉴相器等构成。

对于环路滤波器，为了节省系统的硬件逻辑资源，简化计算，在不影响系统正常运行、确保误差在允许范围内，对环路系数的小数部分进行数据处理，将其转换为近似相等与2 的负整数次幂的值，这样就可以直接采用右移法对环路进行运算。

NCO 模块主要功能是产生同相的相干载波，然后通过低通滤波器得到数字基带信号，可以利用直接数字式频率合成器（DDS）原理实现NCO 功能。在设计时，为了减少ROM 占用的硬件资源，只在ROM 中存储1/4 周期的余弦波对应的值，其他周期的的值通过算法来计算。

希尔伯特鉴相器由4 个乘法器、2 个加法器以及1个实现反三角函数运算的CORDIC 算法模块[13]组成，其结构如图4 所示。乘法器和加法器采用QuartusⅡ中的IP 核即可生成，CORDIC 算法模块采用16 级流水线设计，将x0、y0和θ=0 导入到寄存器中，利用流水线对n 个固定的右移结构实现n 次迭代，这种结构尽管没有将逻辑资源的利用率降低，但是采用了较为简单的右移结构，简化了逻辑结构，有效提升了系统的时钟性能。此外，采用流水线结构也可以提高算法的运行速率，相比直接循环式结构的实现方法，速率提高了n倍，是高速系统中的关键点。反三角函数对应的值存放在ROM 中，可以减少资源占用空间。

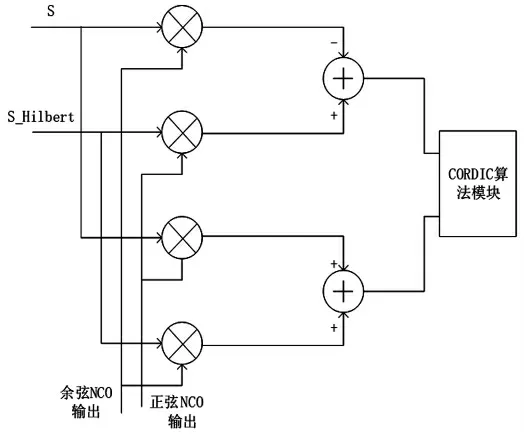
图4 希尔伯特鉴相算法模块

4.2 位同步的硬件实现

本文采用Gardner 定时同步环路实现位同步，由内插滤波器、定时误差检测、环路滤波器以及NCO 模块构成。其中环路滤波器与NCO 模块与内插滤波器模块使用Farrow 结构，实现了基于拉格朗日多项式的立方插值滤波器功能[14]，该结构的滤波器由FIR 滤波器实现，滤波器参数由仿真工具FDATOOL 得到。

4.3 硬件测试结果

硬件实现和模拟BPSK 通信搭建的现场可编程门阵列（FPGA）硬件仿真环境如图5 所示。

图5 BPSK 通信实物图

为了得到与测试结果相比较的绝对基准来评估解调效果，需要得到协议的误码率或丢包率的理论极限，推导出理论极限为

式（8）分别描述了1 bit 信号能量值Eb与有效电压值VSrms和比特持续时间Tb、功率谱密度N0与噪声有效电压VNrms和噪声带宽BW 之间的关系；式（9）为BPSK 解调误码率计算公式；式（10）描述了数据丢包率和误码率的转换关系。

将解调得到的数据导入Matlab 中进行处理，得到数据在传输过程中的丢包率，将理论、实际以及原解调算法所得数据整合，得到丢包率（PER）对比结果，如图6 所示。

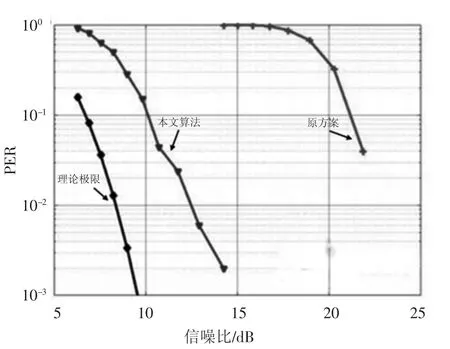
图6 理论、实际及原算法丢包率对比

图6 中由左至右曲线分别为理论极限、本文算法、原芯片解调方案在不同信噪比情况下的丢包率，每一个数据点发送500 个数据包。可以看到，在0.1 PER 值处，TypeB 的理论极限与实际测量结果存在3.1 dB 的差异，这是因为理论极限不包括数据包在开始或结束检测时的错误概率，只包含了误码率。可以看到在PER值为0.1 的情况下，相比原解调算法，本文设计算法所需信噪比环境降低了11 dB 左右，这说明本文设计算法可行，并且性能优于原解调算法。