基于半边数据结构的A-star 路径规划算法及实现

古天驰，李晓东，苏龙生

（佛山科学技术学院 计算机系，广东 佛山 528225）

路径规划在游戏AI 自动寻路、航路规划、人工智能避障以及驾车地图导航等现代计算机科学领域中都有着广泛的应用[1-2]，其主要实现障碍躲避以及最佳路径的选择。A-star 算法则是一种能够达到最优解且常运用于最优路径规划的算法。在路径规划方面，A-star算法通常基于方格地图实现，而方格地图的空间描述局限性较大导致路径选择自由度受限。

传统图的邻接表存储结构复杂而使用不便，导致搜索邻接点、线和面时效率较低。而半边数据结构则是一种基于多边形网格的空间数据结构，常用于三维地图表达，具有较强的拓扑性和灵活性，因此其在计算机图形学、三维建模等领域有着广泛的应用[3-4]。本文提出含邻接边中点信息的半边数据结构，并与利用优化预估代价计算模型的A-star 算法结合，运用于三角网格3D 地图，可突破方格地图的空间局限，有利于提高网格地图的空间利用率，同时提高路径搜索效率。

1 算法原理

1.1 半边数据结构描述

半边数据结构是可用于网格中邻接元素查询的一种数据结构，相较于邻接表方式，半边数据结构更有利于点、线及面的拓扑搜索访问，同时半边数据结构对于网格的表达要求是流形结构[5]，其中三角形是简单的流形结构，故下面是基于三角网格的问题研究。一个网格地图包含点集、边集和面集，其中三角面的每条边为有向边，且逆时针构成环。顶点结构HE_Vertex 包含坐标及其出半边edge 的信息；半边结构HalfEdge 包含目标顶点target、相邻半边pair、下一条半边next 以及所属面face 的信息；面结构HE_Face 包含其中一条半边edge 的信息（图1）。

图1 半边数据结构示意图

为方便A-star 算法在半边数据结构上的应用，在传统半边结构HalfEdge 中添加了边的中点坐标信息center，从而方便路径规划过程中相邻半边的搜索以及最终结果路径顶点的确定，有利于后续A-star 算法基于邻接边中点的路径选择方式的实现（图2）。

图2 含中点信息的半边数据结构三角网格

1.2 HEAS 算法原理

启发式的A-star 算法在路径规划问题中根据终点已有的启发信息来引导搜索，通过计算每一步的代价来决定下一步的去向，代价的计算模型如下所示。

记当前节点自起点累计已花费的代价为G（n），当前节点到达目标点的预估代价为H（n），则当前综合总代价F（n）表示为

记2 个相邻路径节点V1（x1，y1）和V2（x2，y2）间的距离计算利用欧氏距离公式

记当前搜索节点为Vn，其前驱节点为Vn-1，目标点为Vg，当前搜索节点与目标点的相连线段经过障碍的合计距离为di，其间经过的障碍半边数为n。传统预估代价H（n）的计算利用欧式距离，下面通过考虑当前节点与终点连线经过的障碍因素对传统预估代价进行优化，得到新的预估代价计算模型，当前已花费代价G（n）及优化的预估代价H（n）分别表示为下列式（3）和式（4）

下面以具有162 个单位三角网格的地图为基础，在均匀分布的地图障碍面积占整个地图的不同比例下，分别对利用优化预估函数的HEAS 算法和传统预估函数运用在A-star 算法中搜索的三角网格数进行对比测试，如图3 所示。

图3 优化的预估函数与传统预估函数的搜索网格数对比

通过测试，可见利用优化后的预估函数，算法搜索的网格数总是小于或等于利用传统预估函数的搜索网格数，且与障碍面积所占地图比例相关，随着障碍面积平均占比的增大，优化的搜索网格数也随之增大。当起点到目标点的路径上不存在障碍时，2 种预估函数的搜索个数相等，而当起点到目标点的路径上存在障碍时，优化的预估函数其搜索网格数总是更少。

HEAS 算法应用于多边形网格地图在搜索路径决定下一步节点时，对于路径节点的选择是沿多边形的邻接边的中点，在三角网格基础上即2 个三角面之间公共边的中点（图4）。

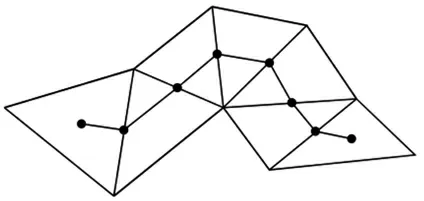
图4 基于邻接边中点的路径选择方式示意图

算法每一步搜索将当前搜索半边所在面的其他2条半边纳入搜索范围，同时利用当前搜索半边的中点计算当前累计的已花费代价G（n）和预估代价H（n），并始终选择两者之和最小即代价最小的半边继续搜索，当遇障碍无法继续搜索时则从搜索范围内的其他半边继续搜索，如此算法则始终体现出整体逼近终点方向搜索的状态。

2 算法的实现

2.1 改进半边数据结构的实现

实现路径规划算法前，首先需要利用含半边中点信息的半边数据结构实现三角网格地图的构造。三角网格地图包含顶点集、半边集和面集，需依次构造单位三角面的顶点、半边以及面结构，并通过对半边结构HalfEdge 添加中点坐标的改进，在构造单位半边结构时，利用半边两端顶点坐标计算出半边中点坐标并进行存储，可方便结果路径的节点获取。

三角网格地图构造过程描述如下：

2.2 HEAS 算法实现三角网格地图最优路径的搜寻

算法执行的辅助结构包含开放队列open，路径前驱节点容器path 以及当前累计代价容器cost。其中开放队列open 为基于小顶堆的优先队列，用其存储等待搜索的半边节点及其优先值，其中优先值按当前累计已花费代价G（n）和预估代价H（n）之和计算，由此确保队头元素总是目前综合代价最小的预搜索半边节点。路径前驱节点容器path 和当前代价容器cost 都是键值对map 容器，path 用于存储已搜索半边节点信息及其搜索过程的前驱半边节点信息，而cost 则存储各半边节点及其自起始点累计已走的距离。

结合上述辅助结构，将利用优化预估代价计算模型的A-star 算法应用于含邻接边中点信息的半边数据结构所构造的三角网格地图的HEAS 算法描述如下：

算法最终所得的结果路径则存储在path 容器的记录中，可从目标节点逐层递推地找到各节点的搜索路径前驱节点，从而通过目标点倒推到起始点找到结果目标路径。

3 实验测试与分析

测试环境所使用的开发工具包括VisualStudio 2019 和OpenGL 应用工具包v3.7 版本，测试用例为半边数据结构构建的三角网格地图，其中包括障碍区域和不可达三角区域，自定义起点和终点并绘制最短路径，以下在基于半边中点的路径节点选择方式下的可达路径进行测试，其中起点和终点的连线为算法所得结果路径，深色网格表示已搜索过的三角面（图5）。

图5 三角网格测试地图示意以及最短路径测试结果

在整体三角面大小较为均匀的地图基础上，以邻接边中点为路径节点的路径选择方式整体较优，可进一步进行三角面细分[6]及利用平滑路径算法来优化冗余路径[7-8]。

在3 个具有不同障碍分布的三角网格地图中基于邻接边中点的路径节点选择方式，分别对Dijkstra 算法、贪心的最佳优先搜索算法（GBFS）以及本文提出的HEAS 算法在搜索网格数量和搜索时间2 个方面的运行情况进行对比，图6 为测试结果。

图6 各路径规划算法对比测试结果

Dijkstra 算法在寻路过程中是以距离起点最近为导向，而GBFS 算法在寻路过程中则是以距离终点最近为导向，但这种贪心思想所得的最终结果未必是最短的路径。HEAS 算法则是在两者中取得平衡，在寻路过程中以距起点距离和距终点距离综合最近为导向，同时考虑两者代价以做出权衡，所得到的结果路径为最短路径。

可见，当地图中有障碍物时，Dijkstra 算法的结果路径总是最优，但在时间效率上欠佳；最佳优先贪心算法在时间效率上最优，但其结果路径并不总是理想的；而采用居中策略的HEAS 算法所得到寻路时间效率和结果路径则是综合最优的方案。

4 结束语

本文利用含邻接边中点信息的半边数据结构表达地图的三角网格信息，结合改进的预估代价计算模型的A-star 算法以及沿三角形的邻接边中点的路径表达方式，证明了HEAS 算法高效适用于三角形网格的路径规划问题，可以得到综合最优的路径方案，同时三角形网格可从二维空间拓展至三维空间，在解决3D游戏场景以及实际三维地形图中的诸多寻路导航问题中更具优势。