明晰学习路径 提升学习能力

文／朱月红

“有理数”是初中数学学习的起点。同学们在小学学习的运算法则、运算性质，在有理数范围内仍然成立。当然，初中的要求会有所提高。初步学习数系扩充的方法，掌握研究一类数的基本方法，会让数学学习更轻松、有趣。

一、初识“数系扩充”的必要性

我们学过各种各样的数。为了表示物体的个数或者顺序，产生了整数1、2、3 等；为了表示“没有”，引入了数0；有时分配、测量的结果不是整数，需要用分数（小数）表示；为了表示具有相反意义的量，我们又引进了负数……总之，数是为了满足生产和生活的需要而产生、发展起来的（如图1）。

图1 数系的扩充路径

二、类比自然数，再识有理数

同学们还记得小学是怎么研究自然数的吗？先回忆一下，将你的想法与图2进行对比。

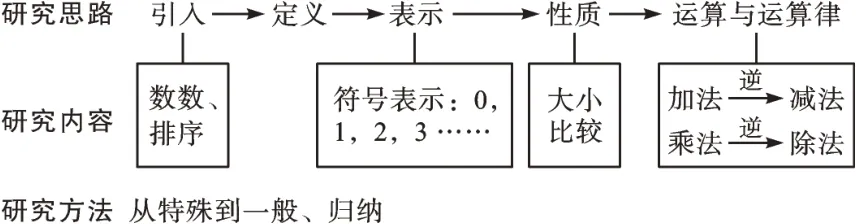
图2 自然数的学习路径

有理数是两个整数的比，是一种具有统一模式（规律）的数，这种模式就是有理数的本质属性。我们可以类比自然数（分数）的学习内容和学习路径来学习有理数。“有理数”这一章的主要内容包括有理数的概念、性质和运算，如图3；研究路径是：引入负数→有理数集→概念→在数轴上的表示（数形结合）→相反数、绝对值→性质→运算。

【小贴士】同学们可以自主建构自己所理解的知识结构图，并将其完善和优化，也可由此流程图想得更远一些，比如，易考点是什么？易错点是什么？创新点在哪儿？未来将继续研究什么？

三、拓展应用，合理运算

数学是讲道理的，数学的计算、证明过程要严谨、有理有据。“有理数”这一章要求的核心能力是运算能力。同学们在学习时，要学会设计运算程序，做到算有方法，算有规矩；探究运算思路，做到算得合理，算得简洁。也就是说，除了会算，同学们还要进一步学习“优算”。

1.明晰运算对象，有序进行计算

学习有理数的运算时，我们可类比小学学过的规则。如分层归纳有理数的加法：第一层按照“正数加正数，正数加负数，负数加正数，负数加负数，负数加0，0 加负数”进行分类归纳；第二层把第一次的归纳结果进一步简约化，并与数轴上点的运动规律建立联系，得到教材上的加法运算法则。依据运算次序、运算法则和运算律进行运算，说明运算步骤的依据，可以培养同学们的推理能力。我们先看一个简单例子。

例1计算：

第一步：观察式子的结构，明确式子中有哪些运算？

第二步：按照运算顺序进行运算。

解：原式=

【小贴士】我们分析算式的运算结构，从有理数的运算法则和运算律出发，通过推理，可以得到有理数混合运算的运算顺序：先算乘方，再算乘除，最后算加减，有括号的先算括号内的式子，能用运算律的尽量用运算律简化运算，从而达到简算、优算的目的。

2.拓展应用，提升学习能力

数学思想是数学知识、数学技能、数学方法的本质体现，是形成数学能力、数学意识的桥梁，是灵活运用数学知识、方法的灵魂。有理数运算主要涉及数形结合、从特殊到一般、分类等数学思想方法。

例2综合运用：学习了“有理数”一章后，小奇对运算产生了浓厚的兴趣。他借助有理数的运算，对于有理数a、b，定义了一种新运算*，满足a*b=a2+b2-|a-b|+1。

（1）分别计算2*（-1）和（-1）*2的值。

（2）试探索这种新定义运算“*”是否满足交换律？请说明理由。

（3）当a=b时，若a*b=3，求出a的值。

解：（1）2*（-1）=22+（-1）2-|2 -（-1）|+1=3；（-1）*2=（-1）2+22-（|-1）- 2|+1=3。

（2）满足交换律。

因为a*b=a2+b2-|a-b|+1，b*a=b2+a2-|b-a|+1= a2+b2-|a-b|+1，所 以a*b=b*a。

（3）因为a*b=3，所以a2+b2-|a-b|+1=3。因为a=b，所以a2+a2-|a-a|+1=3。所以a=±1。

【小贴士】我们可以体会从特殊到一般的思想，感受代数的核心思想，即“引入一种新数，就要研究相应的运算；定义一种运算，就要研究相应的运算律”。

“有理数”这一章涉及的概念较多，同学们可以尝试通过建构数学概念结构图，加深对数学概念的理解，感悟概念的本质，领悟数学研究方法，形成数学学习的一般观念。这样，同学们的学习便能实现从0 到1（从无到有），从1 到n（从有到所有）的蜕变，以及从n到n+1的创造。