采用黑洞-连续蚁群算法的数控车床切削参数优化

赵义豪, 徐莉萍, 张朝阳, 李健, 何奎

(河南科技大学 机电工程学院,河南洛阳 471003)

我国是制造业大国,近几十年来取得了迅猛发展,但是制造业高投入、高消耗的弊端也日益暴露,如何节能降耗、提高能源利用率是当前中国制造业面临的重大问题。机床作为制造业的重要生产工具,其能量利用率平均低于30%,大量的能源浪费也带来了生态环境的污染和CO2排放严重等问题[1-2],而数控车床是使用最为普遍的一种机床,因此,如何在保证产品加工质量的同时降低数控车床的能量消耗,提高资源利用率,是相关行业目前亟待解决的问题。切削参数对数控车床加工起着重要作用,研究表明,通过对加工参数进行合理的优化选择,可以使数控车床能量消耗最高降低40%[3]。因此,在准确建立数控车床切削参数与加工能耗之间的数学模型基础上,提出能够有效降低数控车床能耗的参数优化方法,已成为业界的研究热点。

针对数控车床能耗建模问题,国内外学者进行了大量研究。传统的切削功率建模是通过建立切削参数与切削功率之间的幂率公式,再与加工时间乘积得到切削能耗函数。但该模型涉及多个指数计算,且切削过程中存在载荷损耗,以致准确度不高。为了更方便得到切削能耗值,Kara等[4]提出了能够反映切削能耗与材料去除率关系的切削比能能耗模型;张洪潮等[5]根据切削力经验公式来提出了建立数控车床切削比能幂率公式的方法,并探讨了单个切削参数对切削比能的影响;徐敬通等[6]在文献[5]的基础上研究了双切削参数对切削比能的影响情况;Su等[7]利用支持向量回归方法建立了考虑刀具磨损时的车削比能和加工表面粗糙度的预测模型;Zhou等[8]和Zhong等[9]均建立了以切削参数为自变量的能量预测模型。上述研究均表明不同切削参数组合确实会引起数控车床加工能耗的变化,利用切削比能理念进行数控车床的能耗建模是当前主要的建模方法。

对于切削参数的优化,不仅要考虑对加工能耗的影响,还要考虑对加工质量的影响。因此,如何选择切削参数,同时实现切削能耗和加工表面粗糙度的双目标优化方法的研究受到广泛重视。如Camposeco-negrete等[10]在干切削条件下,利用响应曲面法优化数控车床切削参数选取,使切削比能降低15.69%,表面粗糙度降低26.36%;Nan等[11]利用非支配遗传算法实现了数控车床能量消耗、能量效率和表面粗糙度的多目标优化;Song等[12]着重考虑了切削比能与加工成本,提出动态多种群粒子群算法选择最优切削参数组合,并在AD-35数控车床上得到验证;Li等[13]通过TLBO算法对数控铣床各切削参数进行优化,使切削比能降低5.2%,表面粗糙度减少了10.95%。尽管前人已在机床切削参数多目标优化中取得一定进展,但由于上述优化算法在寻优能力、寻优效率等方面各有局限性,因此还应该对切削参数优化方法进一步深入探索。

连续蚁群算法ACOR(Continuous ant colony optimization algorithm)由Dorigo提出,其比原始蚁群算法更适合解决连续函数优化问题,求解精度更高[14],已在船舶纵向运动参数优化[15]、起重机主梁轻量化设计[16]等工程问题上有所应用,均取得较好效果。ACOR虽然收敛速度快,但由于算法会将每次迭代中的劣解删除,导致其存在易陷入局部最优且自身无法轻易跳出局部最优区域的问题。黑洞算法BH(Black hole optimization algorithm)利用优解指引寻优方向,可以在限定空间内进行充分搜索,有助于提高解的多样性。因此利用黑洞算法对ACOR进行改进,提出黑洞-蚁群算法(BH-ACOR),并应用于数控车床切削能耗和加工表面粗糙度的多目标优化求解。优化结果表明BH-ACOR算法在数控车床多目标优化问题的解决中具有更好的效果。

1 数控车床切削阶段多目标优化建模

数控车床完整的加工过程可划分为主轴启动阶段、主轴空转阶段、进给传动系统空载阶段和材料切削阶段,各阶段功率可表示为启动功率Pstart、空转功率Pidle、空载功率Pempty和切削功率Pcutting。所以,整个加工阶段的总功率可表示为

Ptotal=Pstart+Pidle+Pempty+Pcutting

(1)

材料切削阶段是数控车床能量消耗最大的阶段,而其余阶段主要包含辅助系统运行、主轴旋转、刀架传动等动作,稳定运行后这些系统的能耗成为定值,优化空间不大[17]。数控车床利用进给系统带动刀架上的刀具进行车削以去除多余材料,而切削力Fc是影响切削热和表面质量的直接因素[18]。切削力的变化会直接影响切削加工过程中的切削功率,而车床切削参数又是影响切削力和加工表面质量的主要原因。对于外圆车削加工,切削功率Pc与切削速度vc(m/min)、进给速度f(mm/r)、背吃刀量ap(mm)之间的关系可表示为

(2)

式中:CF、x、y、z为与机床和材料有关的系数;KF为修正系数。

切削比能SEC(Specific energy of cutting)作为衡量加工能效的指标[19],切削比能QSEC表示为

(3)

式中:CMRR为材料去除率,表示每秒去除材料体积的大小,mm3/s。

(4)

联立式(2)～式(4)可得切削比能指数形式的表达式为

(5)

以上公式中的系数与指数值是通过查找切削用量手册确定的,但出现手册规定外的加工条件时选取特定的数值就会变得困难,所以需要根据试验数据进行拟合得到相关系数值。本文引用文献[20]中的试验数据,通过数据拟合以确定引文中加工条件下的式(5)中的系数。试验数据如表1所示。

表1 试验数据[20]Tab.1 Test data

使用1stopt软件拟合得到的切削比能函数,即

(6)

切削比能拟合结果与试验值的对比如图1所示。拟合值与实际值之间的相关系数R=0.98,R2=0.97,表明二者之间的相关性较高,所拟合模型能有效描述切削速度与切削比能之间的关系。

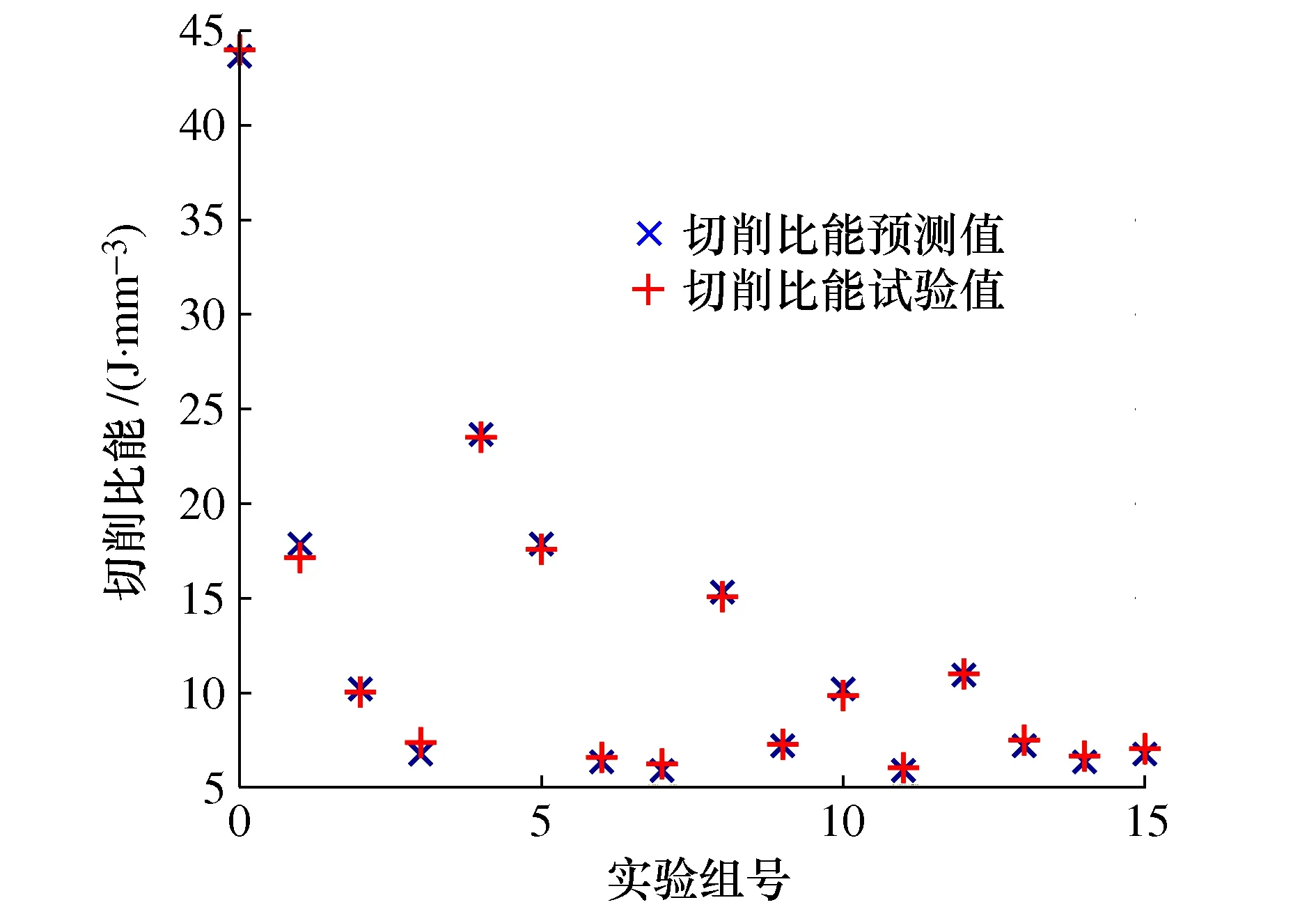
图1 切削比能的预测值和试验值对比Fig.1 Comparison of predictive and experimental values of cutting specific energy

表面粗糙度Ra作为衡量已加工表面质量的常用指标[20],其数学表达式为

Ra=1.598 5-0.006 7vc+0.028 72vcf+

0.002 73vcap

(7)

根据切削比能和表面粗糙度的数学表达式,以及切削参数所必须满足的生产条件限制,可确定材料切削阶段数控车床高能效、高表面质量的多目标优化模型为:

minRa=min(1.598 5-0.006 7vc+

0.028 72vcf+0.002 73vcap)

(8)

多目标优化问题常采用加权求和法将其转化为单目标优化问题。由于切削比能和表面粗糙度的量级不同,还需要对两个目标函数进行归一化处理。根据追求的效益目标不同,对每个优化目标设置不同的权重系数,系数越大表示更加注重对切削比能的优化,反之则追求更低的加工表面粗糙度。

加权后的优化目标函数可表示为

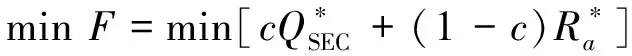
(9)

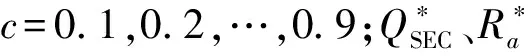
归一化过程定义为

(10)

式中fi,max和fi,min分别为每个目标函数单目标优化时的最大值和最小值。

2 采用黑洞-连续蚁群算法求解最优切削参数

2.1 连续蚁群算法概述

连续蚁群算法(ACOR)是在一般蚁群算法的基础上使用了高斯核函数进行取样来构成新解,将离散搜索空间扩展到连续空间。对于n维优化问题,设初始蚂蚁种群数量为k,则每个蚂蚁可表示为

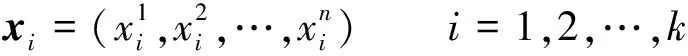
(11)

ACOR在每次迭代时采用高斯核函数根据一定的选择概率由该k个解产生m个新解(m个新蚂蚁),然后把这k+m个解重新排序,只取前k个优解置于解档案中用于下次迭代,后m个劣解则舍弃。通过这种选择、更新、舍弃的方式,当解档案中存放的解逐步趋于一致,此时的解即为所寻找的最优解,具体步骤如下:

步骤1 在定义域内随机生成k个蚂蚁,根据式(9)计算他们的函数值F(xi),并根据结果从小到大进行排序。

步骤2 根据排序编号i,计算每个解的权重ω

(12)

式中:q为强化因子,其值越小算法更趋向于选择排序靠前的解。

步骤3 计算每个解被选择的概率pi

(13)

步骤4 根据步骤3的概率选择一个指导解xi,采用加权高斯核函数Gj(x)对xi的n个维度进行m次采样。采样过程表示为

(14)

式中:j=1,2,…,n;μij为均值,μij=xij;σij为标准差。

(15)

式中:ξ为偏移距离比,其值大于0,ξ值越大则算法收敛速度越慢。

步骤5 采样产生新的m只蚂蚁后,再次根据式(9)计算他们的函数值F(xi)并与之前的k只蚂蚁合并,按照函数值从小到大进行排列,从这k+m个蚂蚁中取出前k个结果视为较优解置于解档案中,后m个视为劣解而舍去。然后返回步骤2,直到迭代终止。

2.2 采用黑洞-连续蚁群算法的切削参数优化

ACOR虽然有收敛速度快的特点,但由于寻优过程中解的多样性过低,容易陷入局部最优。ACOR在运行一段时间后,相对较优解被选作为指导解的概率过大,导致标准差向量σij后续逐渐趋向于0,无法产生新解,解的多样性消失。由于数控车床能耗优化模型是两目标、三变量的非线性函数,其可能具有多个局部最优点,所以传统连续蚁群算法无法保证能够跳出局部最优区域。为解决这个问题,引入黑洞算法[21]与ACOR相结合形成黑洞-连续蚁群算法(BH-ACOR)。BH-ACOR的特点是对ACOR步骤5中解档案的优解和劣解都做出处理。将前k个较优解视为黑洞,后m个劣解视为行星,吸引每个行星朝黑洞所在方向移动以进行全局搜索,且黑洞之间互相不吸引,以期望在移动过程中发现更好的解,从而扩大寻优范围,提高解的多样性。而对于黑洞本身使用局部搜索策略,以提高寻优精度。

由于有3个切削参数作为变量进行寻优,所以维度n为3,则构造的三维解档案结构如图2所示。

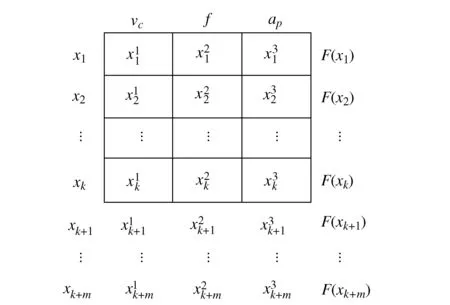
图2 解档案的构造Fig.2 Construction of solution files

在式(8)限定的搜索空间内随机生成k个蚂蚁,则包含3个变量的第i个蚂蚁的位置可表示为

(16)

沿用ACOR步骤2～步骤4,生成m个新解。由于仅有3个切削参数,采样生成的新解数过多会产生相同解出现的情况,对后续寻优造成不利影响,所以本文将m设为50。利用式(9)计算出每个解对应的函数值后进行排序,将前k个使切削比能和表面粗糙度值相对较小的切削参数值置于解档案中视为黑洞,后m个解视为行星。

对于行星,他们将朝向黑洞移动以进行全局搜索生成新的m个解,其搜索算法可表示为

Xi,j=Xi,j+(Xb,j-Xi,j) ·rand(0,1)

(17)

式中:i为第i个行星,i=1,2,…,50;b为第b个黑洞,b=1,2,…,k;j为第j维,j=1,2,3;Xi,j为第j维上第i个行星的位置;Xb,j为第j维上第b个黑洞的位置。

由于黑洞能吸收它周围的物质,所以当行星移动完成后,如果进入黑洞的吸收半径Rb内就会被黑洞吸收。为保证搜索空间内行星总数保持不变,黑洞吸收了多少行星,就要在搜索空间内补充等量的行星,并保证新生成的行星不在吸收半径Rb内。对于多目标优化问题,将吸收半径Rb的计算定义为

(18)

式中:Fb为第b个黑洞的函数值大小;Fi为第i个行星的函数值大小。

对于黑洞,原始黑洞算法认为它具有比行星更优的函数值,不会让黑洞产生移动[22]。但针对数控车床能耗的非线性函数优化问题,黑洞附近是可能存在全局最优解的。为提高解的精度,BH-ACOR算法令k个黑洞在其半径为Rb的空间内进行局部搜索再生成新的k个解。黑洞进行局部搜索过程可表示为

Xb,j=Xb,j+rand·Rb

(19)

最后,将行星和黑洞有关的2m+2k个解进行排序,并取前k个解来更新解档案后进入新一轮的迭代计算。黑洞-连续蚁群算法流程如图3所示。

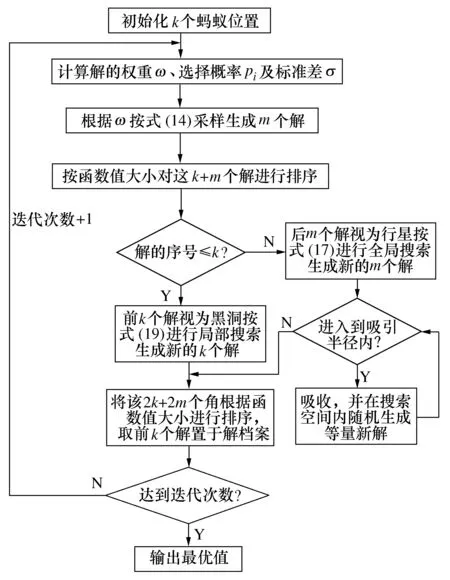
图3 黑洞-连续蚁群算法流程图Fig.3 BH-ACOR flow chart

3 优化结果分析

针对数控车床能耗和表面粗糙度的优化问题,使用MATLAB 2016a编写了基于BH-ACOR优化程序,程序中所使用的算法参数如表2所示。

表2 黑洞-连续蚁群算法参数设置Tab.2 BH-ACOR parameter settings

当多目标优化函数的权重系数c设为0.5,算法运行到第50代、第100代、第200代时切削参数的搜索结果如图4～图6所示。当算法运行到第200代时搜索结果已经收敛,黑洞的位置集中出现在vc=249.94 m/min、f=0.067 mm/r、背吃刀量ap=0.48 mm附近,可见此处存在切削参数最优值。

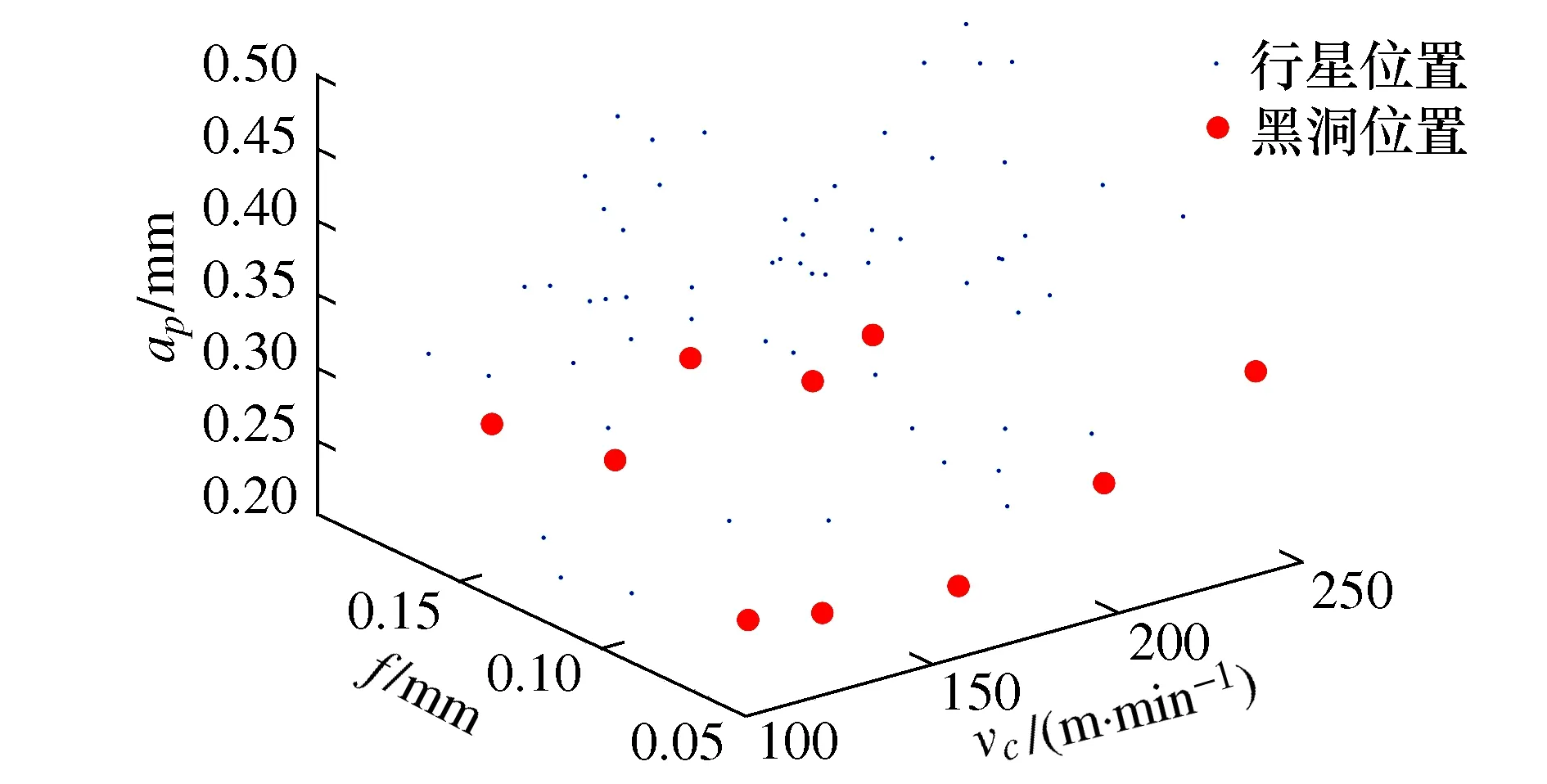
图4 迭代50次时的搜索结果Fig.4 Search results for 50 iterations

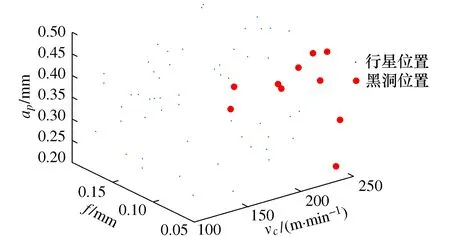
图5 迭代100次时的搜索结果Fig.5 Search results for 100 iterations

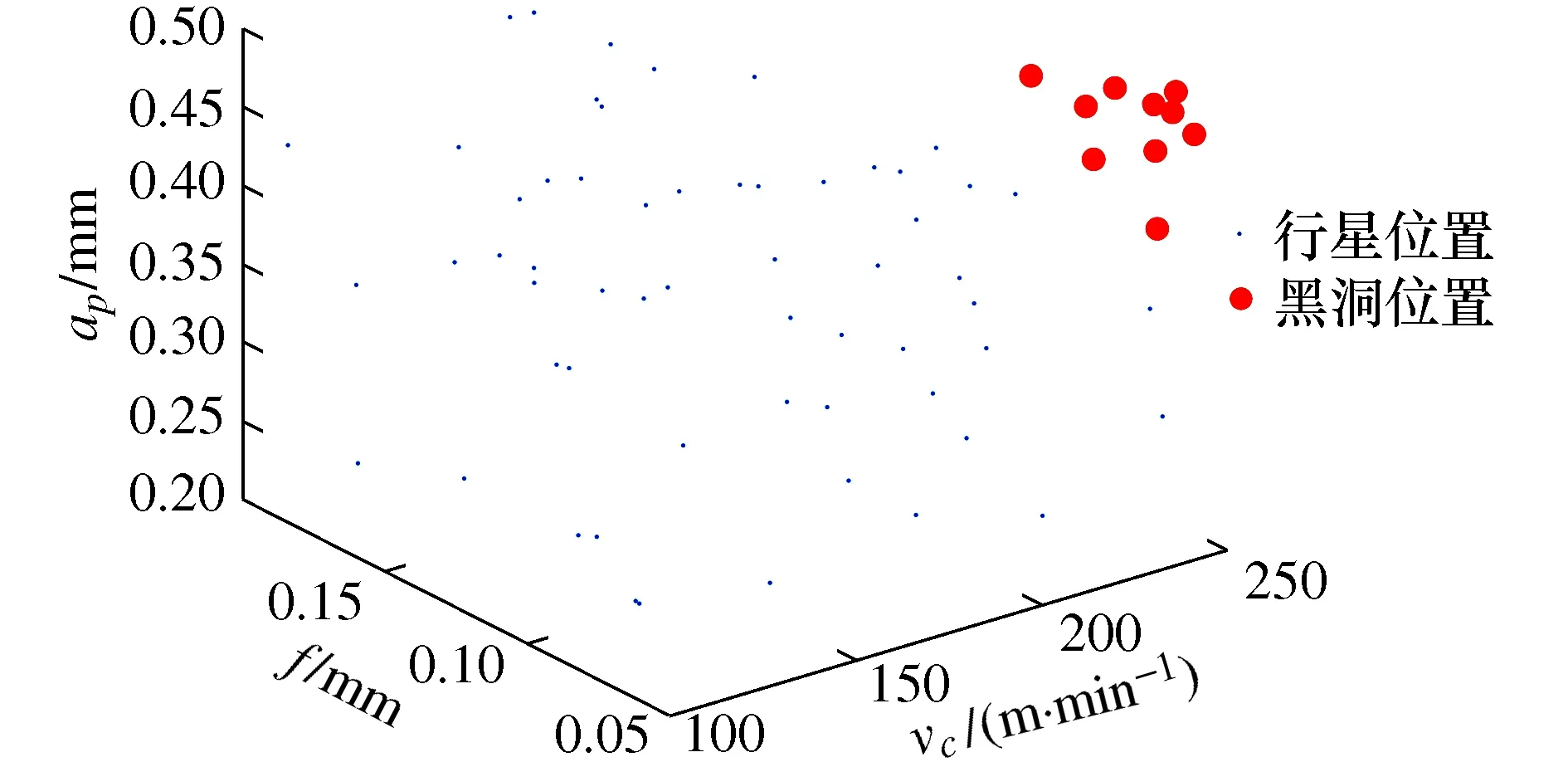
图6 迭代200次时的搜索结果Fig.6 Search results for 200 iterations

不同取值的权重系数c对应得到的切削比能和表面粗糙度的优化结果如表3所示。

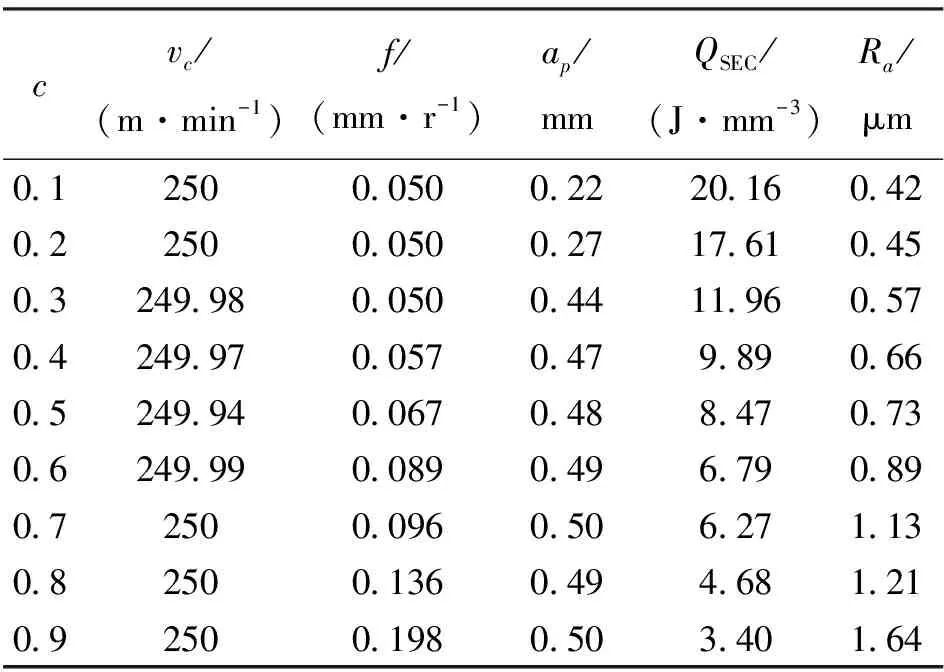
表3 不同权重下的优化结果Tab.3 Optimization results under different weights

由表3可见,优化后切削速度全部接近设置上限250 m/min,说明采用较高的切削速度能够降低切削比能、改善表面质量。选取较大的进给速度和背吃刀量有利于降低切削比能,但会使表面粗糙度升高。同时也应看到,当c=0.1～0.3时,进给速度值全部选于参数设置下限0.05 mm/r,此时背吃刀量是影响二者变化的主要因素;而当c=0.6～0.9时,背吃刀量对二者影响开始变得有限,其值接近设置上限0.5 mm,此时进给速度成为主要影响因素。从整个优化结果看,随着权重系数c的取值增大,切削比能从20.16 J/mm3逐步降为3.40 J/mm3,表面粗糙度Ra从0.42 μm逐步升为1.64 μm,这也就意味着追求切削比能的优化,是要以舍弃表面质量为代价的。

在实际加工中,Ra=0.8 μm时就已经能够满足加工表面质量要求,因此将采用BH-ACOR算法c=0.5时的切削参数优化结果与采用经验加工参数时进行对比,如表4所示。可以看到,利用BH-ACOR算法对切削加工参数优化后,切削比能从9.91 J/mm3减少到8.47 J/mm3,减少约14.5%;表面粗糙度Ra从1.19 μm降到0.73 μm,降低约38.7%。优化结果表明所提出的BH-ACOR优化方法不仅可以提高加工效率,降低能量消耗,同时也使得加工表面质量得到明显改善。

表4 优化结果对比Tab.4 Comparison of optimization results

为了验证算法性能,将BH-ACOR算法与文献[14]中的ACOR算法、文献[20]中的NSGA-Ⅱ算法得到的SEC和Ra的优化结果对比如图7所示。

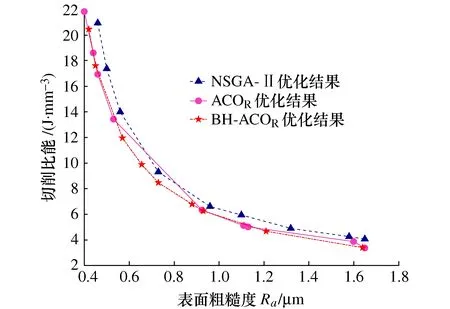
图7 BH-ACOR与其它算法优化结果对比图Fig.7 Comparison of optimization results between BH-ACOR and other algorithms

可以看到,所提的BH-ACOR算法与ACOR算法虽然在搜索结果上相差不大,但ACOR算法的搜索结果在c值为0.4和0.5的两边分布较多,而BH-ACOR算法的结果分布相对均匀,说明BH-ACOR算法在一定程度上避免了局部最优问题;从寻优能力上看,BH-ACOR算法相比于NSGA-Ⅱ算法的结果整体更优,优化效果平均提高约9.58%。

4 结论

建立了以切削比能、加工表面粗糙度最小的数控车床多目标优化模型,提出了黑洞-连续蚁群算法以寻找最优车削参数组合。该优化算法将连续蚁群算法与黑洞算法相结合,扩大了算法搜索范围的同时提高收敛精度,也解决了连续蚁群算法易陷入局部最优的问题。利用黑洞-连续蚁群算法优化后的切削参数比经验参数下加工获得的切削比能值和表面粗糙度有大幅降低。相比于ACOR算法和NSGA-Ⅱ算法,BH-ACOR算法不仅寻优范围更大,优化效果也综合提高约为9.58%。因此BH-ACOR算法能实际兼顾加工能效和加工质量的要求,为帮助企业优化加工工艺,选取合适加工参数组合提供了有效解决方案。