电池包箱体跌落挤压动力学分析与结构优化

许莎, 陈浩, 杨亚莉, 蔡丽红

(上海工程技术大学 机械与汽车工程学院,上海 201620)

随着我国电动汽车的快速发展,电池包作为电动汽车的核心部件在电动汽车上的应用日益增多,电池包在使用及储运过程中的安全问题也日益凸显出来[1]。在激烈的外力作用下,电池包的模组容易起火甚至发生爆炸,严重威胁到司机和乘员的安全。电池包箱体是动力电池的主要载体,对保证整个电池包的安全起着至关重要的作用。因此,对电池包箱体进行动力学分析和结构优化,使箱体满足不同工况下的力学要求,对提高电池包的碰撞安全性具有重要的意义。

近年来,电池包箱体的结构设计和安全性方面的研究逐渐成为热点。在结构设计方面,国内外的研究主要集中在使用复合材料、轻质合金等轻量化材料对电池包箱体进行轻量化设计或采用尺寸优化、拓扑优化以及形貌优化等优化方法对电池包箱体进行结构设计。Hartmann等[2]采用形貌优化,在提升箱体固有频率的基础上减轻了箱体重量。Wang等[3]提出了综合考虑静刚度和动频率的电池箱体拓扑优化方法。Shui等[4-7]以质量、固有频率和变形为设计目标,对电动汽车电池包箱体进行尺寸优化。Zhang等[8]对钢、铝、铜和碳纳米管等不同电池包箱体的最大等效应力和共振频率进行了分析,结果表明碳纳米管在各方面表现较好。李明秋等[9-10]对电池包箱体上盖采用形貌优化,下箱体采用复合材料优化,实现了轻量化设计。冷晓伟[11]通过拓扑优化提升了电池包箱体的强度、固有频率和疲劳寿命。谢晖等[12]对铝合金一体式电池箱上盖进行了形貌优化,轻量化的同时提高了箱体的刚强度。兰凤崇等[13]建立了电池包箱体多材料选材与优化设计流程,实现了电池包综合性能提升。

在安全性研究方面,一般从结构的模态分析入手,进而讨论电池包的振动特性或碰撞条件下的动态响应,并在此基础上提高电池包箱体的耐冲击性能。冯富春等[14]将箱体吊耳的斜面改为直面,从而提升了电池包的抗挤压性能。李志杰等[15]对机械外力如正碰、侧碰及振动冲击下的电池包安全性能进行仿真分析,并提出了综合评价电池包安全的方法和指标。李垚坤等[16]对电池包静刚强度和随机振动进行分析并提出结构改进方案,增强了结构的刚强度。岑波等[17]对电池包进行挤压和机械冲击分析,考察电池包的机械冲击性能。匡松松等[18]在动力学仿真中引入延性损伤准则,提高了电池包挤压仿真的准确度。

目前的研究中,对电池包箱体的研究多为对其单一特性的优化与验证,本文综合考虑电池包在使用和储运过程中经常出现的跌落和挤压问题,采用多样的跌落方式、复杂的挤压工况分析电池包箱体的动态响应。针对现用电池包箱体在结构设计上的不足,建立优化设计流程,综合跌落和挤压工况优化电池包箱体的耐撞性和抗挤压强度,改善电池包箱体安全性能。

1 电池包箱体跌落及挤压动力学分析

1.1 电池包箱体跌落分析

本文对某电动物流车的动力电池包进行研究。整车总质量245 0 kg,整备质量136 5 kg,最高时速80 km/h,电池总电量38.95 kW·h,设计续航里程260 km。整个电池包主要由箱体、模组、控制系统和冷却系统组成,安装在物流车底部,电池模组重327.1 kg,电池包总重386.6 kg。电池包箱体跌落分析的有限元模型如图1所示。整个模型共803 663单元,模组采用六面体实体单元,箱体选用四边形壳单元。电池包上下箱体螺栓连接孔刚性连接,模组与电池包下箱体采用共节点连接。为了防止各部件间发生相互穿透,电池包箱体设置自接触[19],电池包下箱体与刚性地面设置面接触。

箱体材料为普通碳素结构钢,采用Johnson-Cook材料模型,包含应力硬化、应变率的影响[20]。模组定义为弹性材料。箱体和模组的材料基本参数如表1所示。

表1 材料基本参数Tab.1 Basic parameters of materials

1.1.1 电池包箱体不同高度跌落分析

分别对电池包箱体在不同跌落高度和不同跌落角度下的工况进行了跌落冲击仿真。结合试验标准[21]以及电池包在运输过程中可能出现的跌落高度,选取了5个高度h进行分析,h分别为0.8、0.9、1.0、1.1、1.2 m。为了节约计算时间,将高度直接换算成触地时的速度,5个跌落高度对应的速度分别为3.96、4.20、4.43、4.64、4.85 m/s。为防止在初始计算时箱体和地面已经接触并发生相互作用,计算时电池包的离地高度设置为2 mm[22]。图2是h分别为0.8、0.9、1.0、1.1、1.2 m跌落时与地面接触瞬间的最大等效应力。从图2可以看出,当高度为0.8 m时,最大等效应力是325.5 MPa,当跌落高度为1.2 m时,最大等效应力是331.1 MPa,后者比前者增大了1.72%。电池包箱体最大等效应力虽然随着跌落高度的变大而增大,但变化趋势缓慢。因此在0.8 m到1.2 m的跌落高度范围内,跌落高度对最大等效应力的影响不明显。

在进行大变形和冲击分析时,由于离散单元的局限性,通过等效应力考察结构的失效往往数值偏大,而工程应用中有效塑性应变是考察大变形和冲击时的有效指标[23]。不同跌落高度下,电池包箱体受到的冲击载荷不同,因此具有不同的有效塑性应变[24]。所有跌落高度的有效塑性应变最大值都位于下箱体底部凸起处,与地面直接接触的位置。对应于跌落高度h分别为0.8、0.9、1.0、1.1、1.2 m时的有效塑性应变分别为0.085 75,0.096 25,0.106 8, 0.116 3, 0.126 6。可以看出,不同跌落高度下最大有效塑性应变均大于安全容限0.03,箱体结构强度不足,有可能在跌落时遭到严重的破坏。1.2 m时最大有效塑性应变比0.8 m时增大了47.64%,因此跌落高度对有效塑性应变影响很大。

1.1.2 电池包箱体不同角度跌落分析

本文基于实际储运过程中电池包箱体可能的跌落角度设计了1 m高度跌落时4个不同跌落角度α的接触冲击分析,α分别为5°、10°、15°和20°。图3所示为不同角度下电池包箱体的等效应力分布情况。由于等效应力是由电池包箱体触地时刻速度以及与地面接触面积决定,因此4个跌落角度下的最大等效应力发生在不同时刻。

图3 不同跌落角度的等效应力Fig.3 Equivalent stress at different drop angles

从图3可以看出,最大等效应力随跌落角度的增大而减小,跌落角度α=5°时的最大等效应力是331.6 MPa,跌落角度α=20°时的最大等效应力是326.7 MPa,相差4.9 MPa,变化幅度不大。因此,在α=20°的范围内,跌落角度对最大等效应力并没有多大影响,表明跌落角度不太可能导致等效应力骤然增大。

电池包箱体在α分别为5°、10°、15°和20°跌落下的最大有效塑性应变分别为0.240 2,0.225 1, 0.211 3,0.189 0。最大有效塑性应变基本都位于与地面接触的箱体底部。跌落角度α=5°时的有效塑性应变最大,是角度跌落的较薄弱工况。跌落角度α=20°的有效塑性应变最小,比5°的有效塑性应变减小了20.83%,说明跌落角度对有效塑性应变有显著影响[25]。

1.2 电池包箱体挤压分析

1.2.1 等效应力和有效塑性应变

本文对电池包箱体横向和竖向挤压两种方式进行动态分析。挤压板采用刚性材料模拟,假设挤压过程不发生弹塑性变形。无限大的刚性平面位于电池包箱体的底面及侧面。电池包箱体不同方向的挤压分析模型如图4所示。

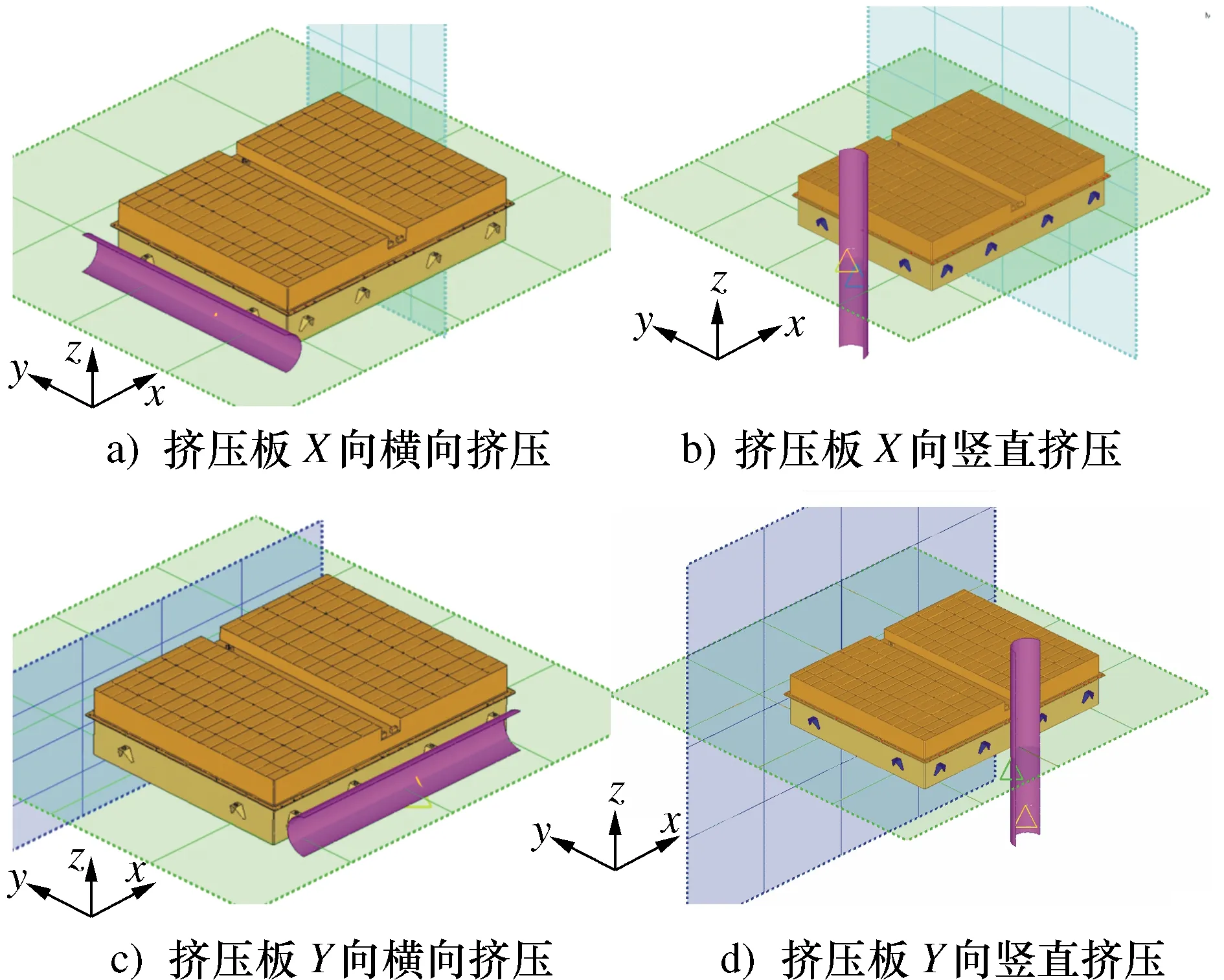
图4 电池包箱体挤压模型Fig.4 Extrusion model of a battery pack box

国家标准规定在100 kN的挤压力下,电池包不能起火和爆炸。因此需要对挤压板达到100 kN挤压力时电池包的变形状态[26]进行重点查看。4个挤压工况下的等效应力如图5所示。横向挤压时,挤压板直接作用于吊耳处,导致应力最大值极易出现在吊耳处,竖直挤压下,受力方向上的面较易出现应力集中。

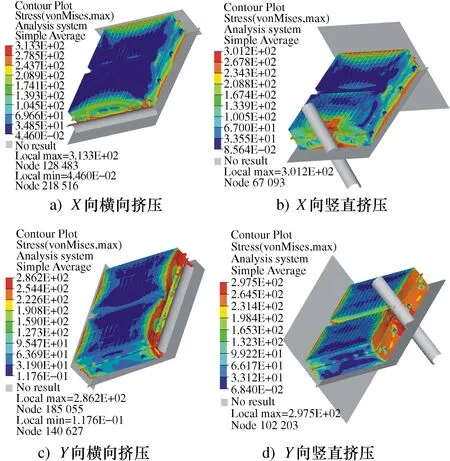
图5 电池包箱体挤压分析的等效应力Fig.5 Equivalent stress of battery pack box extrusion

由图5可知,4种挤压工况下,Y向横向挤压时电池包箱体的应力值是286.2 MPa,此时的最大等效应力最小;X向横向挤压时电池包箱体的应力值是313.3 MPa,此时的最大等效应力最大。不同挤压工况对等效应力的影响较小,X向横向挤压时箱体较为薄弱。电池包箱体X向横向、X向竖直、Y向横向及Y向竖直挤压4种工况下的最大有效塑性应变分别为1.235,0.836 7,0.640 5,1.453,大于安全容限0.03,电池包箱体总体的有效塑性应变过大,说明电池包箱体的强度不足,极易在挤压工况下产生撕裂现象。

1.2.2 吊耳侵入量

本文分析4种挤压工况对吊耳侵入量的影响,吊耳变形如图6所示。

图6 吊耳变形Fig.6 Deformation of lifting lug

由图6可以看出,吊耳的变形量很大,说明在挤压工况下,吊耳对碰撞能量吸收贡献很大。挤压工况中,吊耳对电池包箱安全性能有较大影响,而过大的吊耳侵入量会导致电池包箱体过早出现变形[27],威胁模组安全。X向横向、X向竖直、Y向横向及Y向竖直挤压4种工况下,吊耳侵入量分别为19.1 mm、13.1 mm、11.6 mm、13.2 mm。X向横向挤压吊耳侵入量最大,Y向横向挤压时吊耳侵入量最小。最大吊耳侵入量比最小侵入量多64.7%,过大的吊耳变形量说明电池包箱体抗挤压能力不足。

1.2.3 下箱体侵入量

判断模组是否受到挤压,主要的评价参数是下箱体侵入量。为保护模组安全,一般要求下箱体最大侵入量小于受力方向模组与箱体的原距离。本文的电池包模型,X向挤压的安全距离是16.9 mm,Y向挤压的安全距离为48.3 mm。图7为下箱体在4种挤压工况下的变形云图。

从图7可以发现,竖直挤压工况下高变形区域比横向挤压工况小,但最大变形量比横向挤压工况要大,说明竖直挤压工况更容易压溃箱体。X向横向和X向竖直挤压的最大侵入量分别为19.2 mm和20.3 mm,最大值都大于X向的安全距离16.9 mm,其中X竖直挤压时安全隐患最大,超出安全距离20.1%。Y向横向和Y向竖直挤压的最大侵入量分别为41.3 mm和51.7 mm,Y向横向挤压侵入量小于安全距离48.3 mm,Y向竖直挤压侵入量大于安全距离7%。考虑4种工况下的侵入情况,本文现用电池包箱体不符合安全要求。

2 电池包箱体多目标优化

2.1 电池包箱体跌落优化设计

分析电池包跌落仿真中的等效应力和有效塑性应变,可以发现电池包箱体强度的薄弱点大都位于电池包下箱体的底部。因此,本文选取上箱体厚度和下箱体厚度作为优化设计变量,通过改变箱体尺寸参数增强电池包箱体强度。考虑到电池包箱体材料的工艺以及钣金件的加工要求,上箱体和下箱体厚度的设计范围为1～3 mm。以等效应力、有效塑性应变、重量最小化为目标,以电池包箱体跌落分析中的易破坏区域应力和有效塑性应变为约束,建立优化模型。利用HyperStudy结构优化求解器,在现有的电池包箱体结构上开展优化设计,定义25次计算,观察每次计算变量和对应响应量的值,选择最佳参数组合。跌落优化前后的结果对比如表2所示。

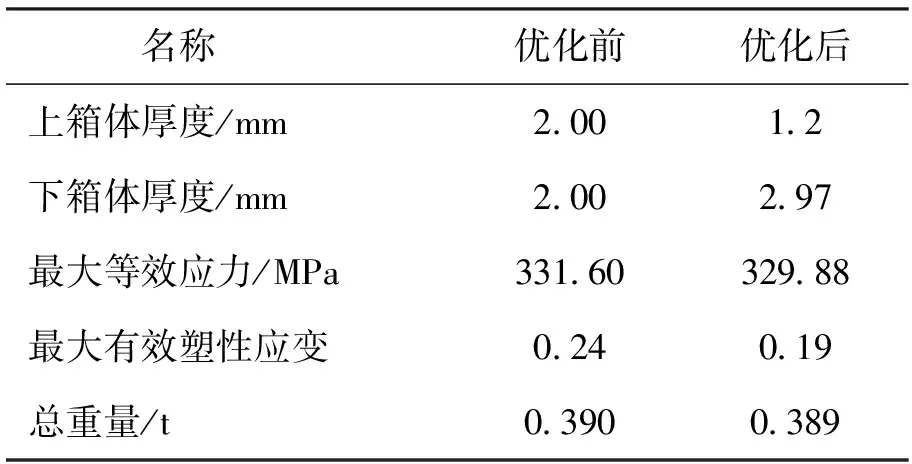
表2 跌落优化前后对比Tab.2 Comparison before and after drop optimization

由表2可知,为了提高电池包箱体耐撞性能,通过增加下箱体厚度到2.97 mm以及上箱体厚度减小到1.2 mm,使电池包箱体的最大有效塑性应变减小了20.8%,最大等效应力和总重量略有降低,提升了电池包箱体的跌落碰撞性能。

2.2 电池包箱体挤压优化设计

为了增加吊耳在变形时吸收的能量,减缓冲击,挤压优化中选取上箱体厚度、下箱体厚度和吊耳厚度作为设计变量,考虑到电池包箱体材料的工艺以及钣金件的加工要求,上箱体和下箱体厚度的设计范围为1～3 mm,吊耳厚度的设计范围是1～4 mm。挤压优化设计以等效应力、有效塑性应变、侵入量最小化为研究目标,结合电池包箱体挤压分析中的薄弱区域为约束条件,建立挤压优化模型,得到挤压优化前后结果对比如表3所示。

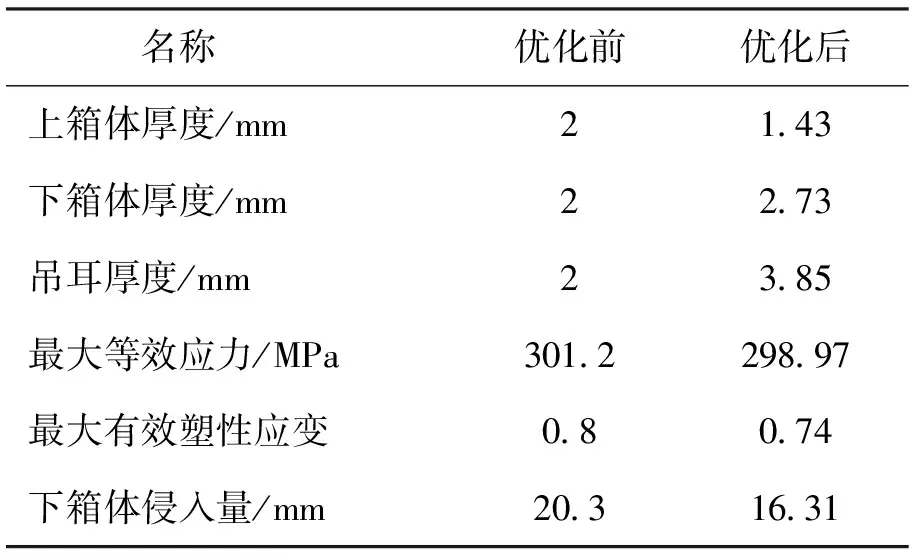
表3 挤压优化前后对比Tab.3 Comparison before and after extrusion optimization

由表3中可知,下箱体侵入量为16.31 mm,比优化前20.3 mm降低了19.7%,维持在安全距离以下,很好的增强了模组的安全性能。最大有效塑性应变降低7.5%,最大等效应力减小了0.7%,优化方案能有效降低响应量,提高电池包箱体安全性能。

2.3 电池包箱体优化结果

根据电池包箱体跌落工况优化得到上箱体厚度1.2 mm、下箱体厚度2.97 mm,根据电池包箱体挤压工况优化得到上箱体厚度1.43 mm、下箱体厚度2.73 mm和吊耳厚度3.85 mm。为了满足两种工况要求,同时提高电池包箱体安全性,取上箱体厚度1.43 mm、下箱体厚度2.97 mm以及吊耳厚度3.85 mm。考虑到钣金件的工艺要求,调整箱体结构参数为上箱体厚度1.5 mm、下箱体厚度3 mm、吊耳厚度4 mm。根据优化后的结构参数对电池包箱体的动力学特性进行分析。

2.3.1 优化后电池包模态分析

优化前后电池包前10阶固有频率的对比情况如表4所示。从表4可以看出,优化后电池包的前10阶固有频率有明显改善。优化后电池包的1阶频率37 Hz与优化前的1阶频率22.2 Hz相比增大了14.8 Hz,高于路面的激励频率21 Hz,能够避免电池包共振现象的发生。

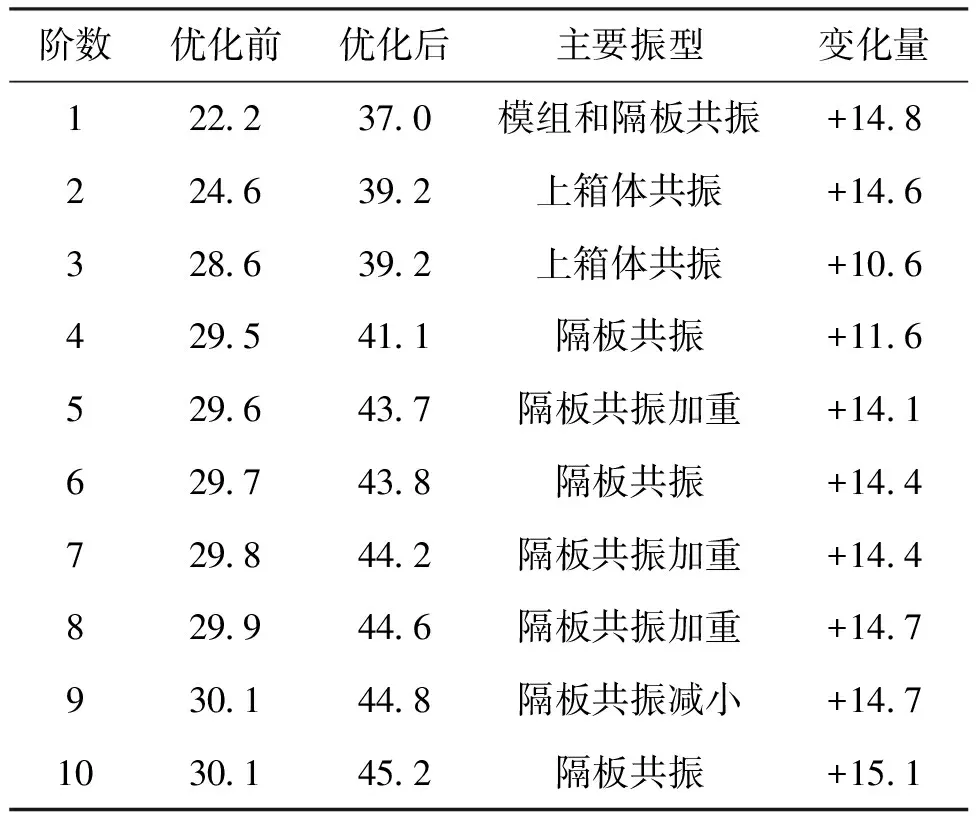
表4 电池包前10阶固有频率

2.3.2 优化后电池包箱体跌落分析

尺寸优化后电池包箱体跌落响应以最大等效应力和最大有效塑性应变作为优化评价标准。电池包箱体跌落分析的等效应力和有效塑性应变情况如图8所示。从图8a)可知,等效应力最大值为328.3 MPa,比较未优化时等效应力最大值331.6 MPa,最大等效应力略有下降。由图8b)可知,有效塑性应变最大值0.19相比优化前的0.24降低了20.8%,因此电池包箱体跌落工况时的安全性能得到了改善。

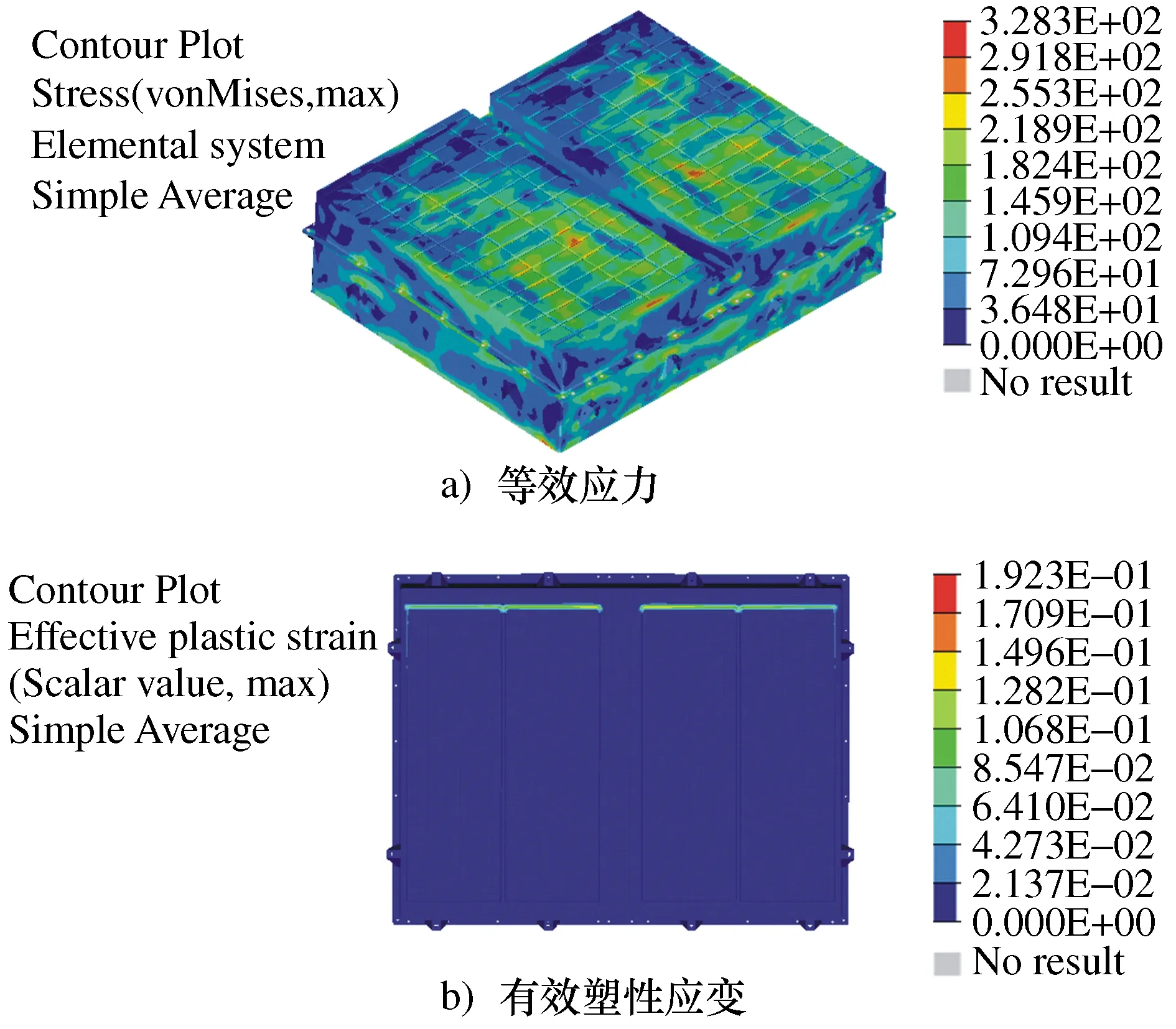
图8 电池包箱体跌落云图Fig.8 Contours of battery pack box drop

2.3.3 优化后电池包箱体挤压分析

图9所示为优化后电池包箱体的等效应力以及下箱体的位移云图。

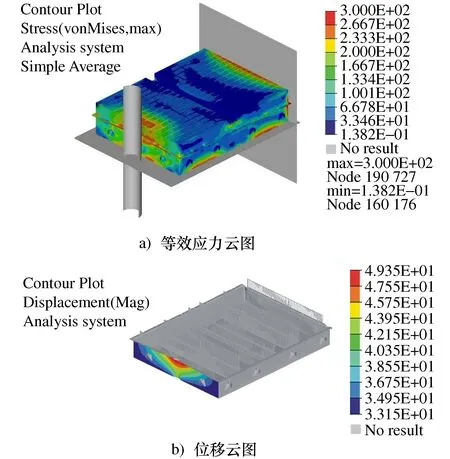
图9 电池包箱体挤压云图Fig.9 Contours of battery pack box extrusion

从图9a)可知,等效应力最大值为300 MPa,比优化前的等效应力最大值301.2 MPa略有减少。优化后的有效塑性应变最大值为0.68,相比优化前的0.8,优化后有效塑性应变降低15%,提高了箱体强度。由图9b)可知,最大侵入量为16.2 mm,相比优化前的20.3 mm,优化后侵入量降低20.2%,小于安全距离16.9 mm,达到电池包箱体挤压标准要求。

2.4 电池包跌落试验

按国家标准[21]要求,蓄电池沿Z轴方向从1 m高度处自由跌落到水泥地面上,观察2 h。考虑到实际储运或安装过程中可能的跌落角度5°,试验跌落高度为电池包倾斜5°时最低点至水泥地面的距离。

将优化后的电池包以1C充放电至厂家规定的截止条件并分别静置30 min,进行预处理,如图10所示。

图10 预处理Fig.10 Pretreatment

然后,将电池包提升到1 m处并倾斜5°,松开电池包让其自由落体撞击地面。跌落试验通过观察试验过程中电池包有无电解液泄露着火或爆炸现象判断其安全性能,试验结果如图11所示。从图11可以看出,跌落试验过程中并没有发生电解液泄露或者爆炸起火现象,电池包箱体底部的变形较小,试验结果满足跌落标准的要求。

图11 跌落试验Fig.11 Drop Test

3 结论

1) 通过探讨不同跌落高度(0.8、0.9、1、1.1、1.2 m)和不同角度(5°、10°、15°、20°)对箱体动态响应的影响,发现有效塑性应变对高度和角度参数敏感程度很高,且最大值都位于下箱体底部,表明下箱体底部为跌落工况的薄弱区域,下箱体容易发生强度破坏。

2) 通过分析X向横向、X向竖直、Y向横向及Y向竖直4种挤压工况下电池包箱体的动态响应,发现X向横向、X向竖直及Y向竖直挤压工况下侵入量都高于电池包挤压安全要求,表明电池包箱体的结构强度不足,存在着压溃现象。

3) 通过多目标尺寸优化,综合考虑跌落和挤压工况,对电池包箱体进行了结构优化设计。对比初始动态特性,优化后,电池包1阶固有频率显著提高,有效的避免了路面和台架试验的振动频率。跌落工况有效塑性应变降低了20.8%,挤压工况侵入量和有效塑性应变分别降低了20.2%和15%,表明电池包的跌落和挤压安全性能在优化后得到了明显的提升。