天目山常绿阔叶林胸高断面积生长量影响因子研究

窦啸文，吴登瑜，张笑菁，汤孟平

（1.浙江农林大学 省部共建亚热带森林培育国家重点实验室，浙江 杭州 311300；2.浙江农林大学 环境与资源学院，浙江 杭州 311300；3.浙江农林大学 林业与生物技术学院，浙江 杭州 311300）

断面积生长模型是森林生长和收获预估的重要基础[1]。目前，在区域尺度上，较为常见的，是基于抽样方法的多个小样地(400～600 m2）调查数据，并用逐步回归的方法[2-4]建立某个树种的单木断面积生长模型，模型的自变量包括林木大小、竞争、地形等因子[5-8]。由于逐步回归法直接剔除共线性自变量，导致完全忽视被剔除变量的影响。岭回归分析是一种专门用于共线性数据分析的有偏估计方法。针对共线性的病态数据，岭回归既保留了全部自变量，又在一定程度上减少了多重共线性对回归结果的影响[9]。但是，岭回归在单木断面积生长模型研究中应用较少。已有研究表明：在群落尺度上，为精准掌握森林空间结构，样地面积至少为2 500 m2[10]。然而，基于群落大型固定样地，建立包含森林空间结构变量的单木断面积生长模型研究少见报道。因此，岭回归分析应用于建立大型固定样地的单木断面积生长模型的问题值得探讨，可以在不剔除自变量的基础上，对含有不同自变量的模型进行比较，定量描述不同自变量对胸高断面积生长量的影响。

常绿阔叶林是中国亚热带最复杂、生产力最高、生物多样性最丰富的顶级森林群落，对保护环境、维持全球性碳循环平衡和人类可持续发展等都具有极重要的作用[11]。目前，对常绿阔叶林的研究集中在空间结构[12-13]、生物多样性[14]、碳储量[15]等方面，而关于单木断面积生长量的研究少见报道。本研究以浙江天目山国家级自然保护区内常绿阔叶林为对象，分析林木大小、竞争因子、地形因子与胸高断面积生长量的相关性，再对不同胸径大小、冠幅和竞争等级的胸高断面积生长量进行差异性分析，最后基于岭回归，建立以胸高断面积生长量对数为因变量的单木生长模型，定量描述胸高断面积生长量与胸径、竞争和地形因子的关系，为常绿阔叶林经营提供理论依据。

基于公司实际情况，优化数据编码管理权限的设置，实现基础数据过程管理规范化流程，规范基础数据（标准编码）的申请、审核、确认的流程管理。在系统应用初期应进行数据编码的集中、统一、归口管理，确保数据源的准确、唯一，随着后期系统应用成熟和编码标准的不断完善和细化，再逐步放权，以此来保证物资管理系统的应用能够不因为数据的问题导致流程效率低下、单据质量不高、频繁驳回的情况。

1 研究区概况

天目山国家级自然保护区位于浙江省杭州市临安区西北部(30°18′30″～30°24′55″N，119°24′11″～119°28′21″E），距杭州市中心94 km，总面积为4 284 hm2。该保护区属中亚热带向北亚热带过渡气候，受海洋暖湿气流影响，季风盛行，气候温和。年平均气温为 8.8～14.8 ℃，最冷月平均气温为-2.6～3.4℃，最热月平均气温为19.9～28.1 ℃。雨水充沛，年降水量为1 390～1 870 mm。森林类型多样，主要有常绿阔叶林、常绿落叶阔叶混交林、落叶阔叶林、落叶矮林、针叶林和毛竹Phyllostachysedulis林等[16]。

（2）对购置崭新的汽车货车等固定资产应该想到最节税的办法方案去执行。在营业税改增值税的方案落实之后，购入机器设备等固定资产的进项税额是可以开始扣除掉的，因此物流公司应该努力想方设法去研究应该在哪个时间点上去购置新的固定资产，以何种方式去购置，购置哪种金额的设备，该设备的预计使用年限及耗损率等等，才能以最优的方式去节税少税。

2 研究方法

2.1 样地设置

“可是蚊子除了，蜻蜓吃什么？蜘蛛吃什么？蝙蝠又吃什么？还有其他的鸟儿，也得将蚊子当饭。要是没有蚊子，万花谷就会少很多生机与生趣。我来谷里几个月，功夫上没什么长进，心里却觉得，每一棵树，每一只动物，每一个人，在这里都是相关的，长在一起，牵一发而动全身，一头白猿在晴昼海里叫几声，可能就会引来一场雨，第二天早上，晴昼海里的草头就会盛开，一片紫颜色。”

2.2 胸高断面积生长量

林木的生长量指一定间隔期内林木各种调查因子的变化量，分为总生长量、定期生长量、连年生长量、定期平均生长量和总平均生长量等[17]。本研究采用2005—2020 年15 a 间林木胸高断面积的定期生长量。计算公式为：

在常绿阔叶林样地内，计算活立木在2005 年时的胸径、冠幅、海拔、坡度、坡向指数、竞争指数及2005—2020 年间胸高断面积生长量的均值、标准差(表1）。对各变量进行Kolmogorov-Smirnov 检验，发现所有变量的显著性都小于0.05，均不符合正态分布，故用Spearman 相关系数进行相关性分析(表2）。结果表明：胸高断面积生长量与胸径、冠幅均呈现极显著正相关(P＜0.01），与竞争指数呈现极显著负相关(P＜0.01），与地形因子的相关系数均不显著。说明天目山常绿阔叶林的林木胸径、冠幅对林木胸高断面积的生长起到正向作用，竞争对林木胸高断面积生长起到负向作用，地形因子对林木胸高断面积生长的影响小。胸径和冠幅均与竞争指数极显著负相关(P＜0.01），说明竞争抑制林木胸径和冠幅的生长。冠幅与海拔极显著正相关(P＜0.01），说明海拔影响林木冠幅的生长。坡向指数与冠幅显著负相关(P＜0.05），说明坡向影响林木冠幅的生长。

式(1）中：BAI为林木胸高断面积生长量(cm2）；Dt1和Dt2分别为林木在t1和t2时的胸径(cm）。

2.3 生长模型的建立

单木生长模型主要有潜在生长量修正法、回归分析法和生长分析法[18]。本研究采用回归分析法，建立林木胸高断面积生长量对数与林木大小、竞争和立地等因子之间的回归方程[5-8]：

式(2）中：BAI为胸高断面积生长量；f(x1)为林木大小因子的函数；f(x2)为林木竞争因子的函数；f(x3)为林木立地因子的函数；a为常数项；b、c、d为方程参数。

在 Excel 2019 中对数据进行预处理。基于林木的三维坐标，利用ArcMap 10.7 插值分析提取坡度、方位角数据；基于 ArcMap 10.7 和 Python 语言编程计算每株林木的竞争指数；在 SPSS 26 中采用Kolmogorov-Smirnov 检验法对各因子进行正态性分析，并利用Spearman 相关系数进行相关性分析；利用SPSSAU 采用Kruskal-Wallis检验法(K-W）和Nemenyi 法分析不同胸径大小、竞争条件下林木胸高断面积生长量的差异性，采用岭回归方法建立单木生长模型。

2005 年，在研究区内选择代表性地段，设置100 m×100 m 的常绿阔叶林固定样地，样地中心地理坐标为： 30°19′40″N，119°26′12″E，并用相邻格子调查法将样地划分成10 m×10 m的网格单元。对网格单元进行每木检尺，记录树种、胸径、树高、活枝下高、冠幅等，并以样地西南角为原点，采用激光对中全站仪(徕卡TCR702）测定每株林木的坐标及海拔。2020 年对该样地进行复查。本研究采用2005 和2020 年2 期调查数据，从中筛选出2 期均存活且胸径≥5 cm 的活立木共计733 株。其中，常绿阔叶优势树种有细叶青冈Cyclobalanopsisgracilis、短尾柯Lithocarpusbrevicaudatus、青冈C.glauca、小叶青冈C.myrsinifolia、豹皮樟Litseacoreana等，占全部活立木的51.99%。

2.4 模型因子的选取

2.4.1 林木大小因子的选取 林木大小是影响林木断面积生长量的最重要因子[6]。林木胸径是反映林木大小的最直观因子，也是预测林木生长最重要的因子之一[19]。林木胸径平方能够很好地表述林木生长趋势，即林木在幼龄时生长速度较快，成熟时生长达到顶峰，随后生长速度开始逐渐下降[2]。此外，用胸径对数进行建模分析也较常见[5-6]。冠幅直接影响林木进行生理活动的能力[20]，因此在林木生长模型中常作为反映林木大小的变量。如 MONSERUD 等[6]发现：冠长率能解释奥地利针叶树种和阔叶树种断面积生长量14%～47%的变异。本研究选取林木的胸径平方、胸径对数和冠幅来代表林木大小。这里，冠幅用冠幅半径表示，计算公式为：

式(3）中：Cr为林木冠幅半径(m）；L1、L2分别为林木东西、南北冠幅半径(m）。因此，林木大小因子的函数表达式为：

式(4）中：D为林木胸径；b1、b2、b3为方程参数。

二是以特定区域或特定社会组织类型人员为调查对象，分析社会组织人才专业化状况。金锦萍（2008）以北京市残疾人康复服务机构为例、Tracy Taylor，Peter McGraw（2006）以体育类社会组织为例、邢博（2011）以上海市基金会为例分别考察社会组织人才现状。罗拾平（2008）以长沙市社会组织为例、尹志刚（2010）以北京市西城区社会组织为例、叶萍（2011）以广东省社会组织为例、罗美侠（2011）以黑龙江省社会组织为例考察社会组织人才现状。

2.4.3 立地因子的选取 地形是影响林木生长的重要因素。如COOMES 等[24]在研究新西兰的森林时，发现随着海拔的升高，林木生长率有下降的趋势；STAGE 等[25]发现：坡度、坡向、海拔的交互作用影响森林的物种组成和森林的生产力；BARIBAULT 等[26]发现：森林地形的差异会导致林木间的生长有很大的不同。根据前人构建的生长模型[5-6]，选取海拔、坡度和坡向作为模型的立地因子。其中，采用坡向指数(As）来代表坡向。坡向指数的计算公式为[27-28]：

式(6）中：c1、c2为方程的参数。

式(5）中：IC为对象木i的竞争指数；Di、Dj分别为对象木i和竞争木j的胸径(cm）；Lij为对象木i与竞争木j之间的距离(m）；ni为对象木i所在竞争单元的竞争木株数。因此，林木竞争因子的函数表达式为：

式(5）中：As为坡向指数；θ为坡向值(0°～360°）。因此，立地因子的函数表达式为：

式(8）中：Al为林木所处的海拔；Sl为林木所处的坡度；d1、d2、d3分别为方程参数。将式(4）、式(6）、式(8）代入式(2）得到最终的林木胸高断面积生长模型：

传统假肢矫形器制作技术是一种典型的手工制作技术，制作过程包括取模、修模、成型加工等步骤，3D打印通过三维扫描仪获得肢体或残肢的数据，再通过相关软件进行设计修改，最后通过设备打印。两种制作方法比较见表1。

2.5 统计分析

根据相关报道，并结合核电站二回路腐蚀产物的分布规律，可以用凝汽器中的磁性过滤器、除氧器筒体内部及蒸汽发生器泥渣沉积量作为水质控制优劣的评价依据[4]。现以某核电站为例，对凝汽器磁性过滤器、除氧器筒体及蒸汽发生器的沉积物进行分析评价。

3 结果与分析

3.1 相关性分析

In the sigma–delta modulator, the noise is mainly determined by the switch-capacitor thermal noise of the first integrator. The sampling phase and integral phase will both contribute to certain noise. In the sampling phase, the input noise power is:

表1 各变量统计结果Table 1 Statistics results of each variable

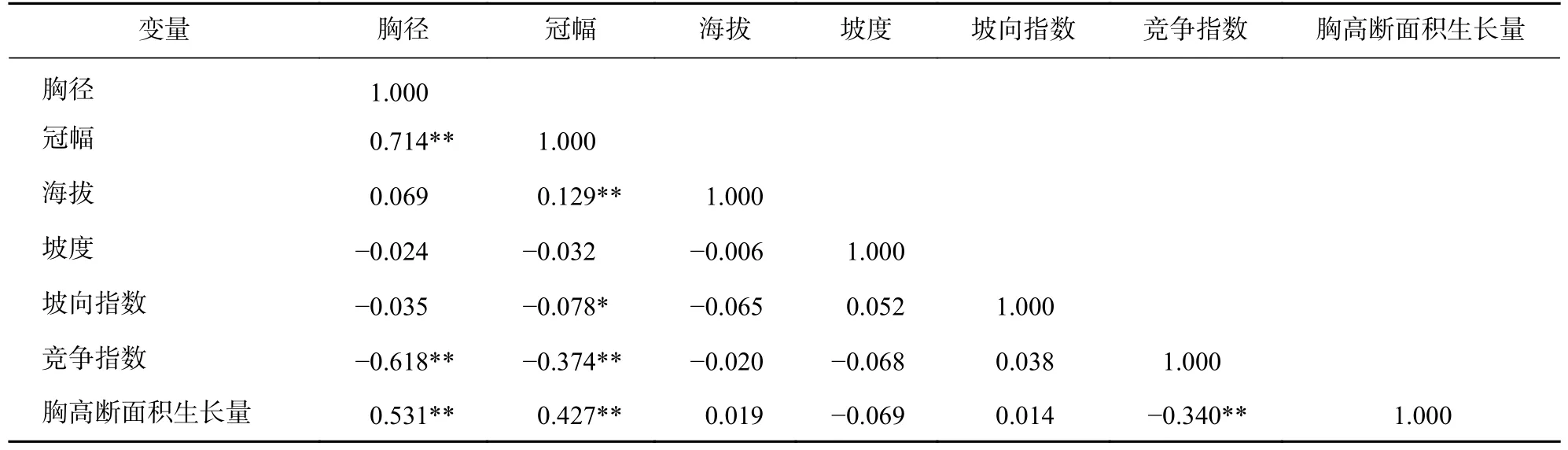
表2 各变量的相关系数Table 2 Correlation coefficients of each variable

3.2 胸径对胸高断面积生长量的影响

样地林木胸径均值为13.15 cm，胸径最小值为5.00 cm，最大值为50.30 cm。根据林木胸径均值和分布范围，将其分为3 个径级：[5.00, 9.00）、[9.00, 13.00）、[13.00, +∞），分别表示为Ⅰ径级、Ⅱ径级、Ⅲ径级。对不同径级林木的胸高断面积生长量进行Kruskal-Wallis 非参数检验。结果显示：Ⅰ径级、Ⅱ径级和Ⅲ径级的胸高断面积生长量中位数分别为22.50、49.68 和86.71 cm2，K-W 检验的统计量(H）=185.84，P＜0.01，存在极显著差异，表明胸高断面积生长量随着林木胸径的增加而增加。用Nemenyi 法进一步证明(图1）：Ⅰ径级、Ⅱ径级、Ⅲ径级林木的胸高断面积生长量两两之间差异极显著(P＜0.01）。说明林木胸径大小是导致胸高断面积生长量差异的主要因子之一。

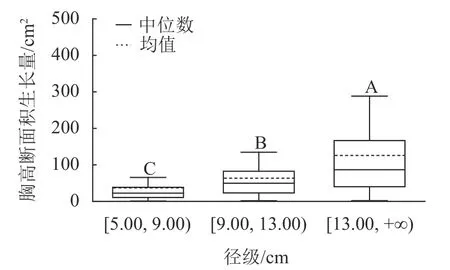
图1 不同径级的胸高断面积生长量Figure 1 Breast-height basal area increment for different diameter classes

3.3 冠幅对胸高断面积生长量的影响

样地林木冠幅均值为1.86 m，冠幅最小值为0.25 m，最大值为6.11 m。根据林木冠幅均值和分布范围，将其分为3 个等级：[0.25, 1.35）、[1.35, 2.45）、[2.45, +∞），分别表示为Ⅰ冠幅、Ⅱ冠幅、Ⅲ冠幅。对不同冠幅等级林木的胸高断面积生长量进行Kruskal-Wallis 非参数检验。结果显示：Ⅰ冠幅、Ⅱ冠幅和Ⅲ冠幅林木的胸高断面积生长量的中位数分别为24.03、37.37 和90.65 cm2，H=96.627，P=0.000＜0.01，存在极显著差异，林木胸高断面积生长量随着林木冠幅的增加而增加。用Nemenyi 法进一步证明(图2）：Ⅰ冠幅与Ⅱ冠幅、Ⅲ冠幅林木的胸高断面积生长量两两之间差异极显著(P＜0.01）。说明，林木冠幅大小是导致胸高断面积生长量差异的主要因素之一。

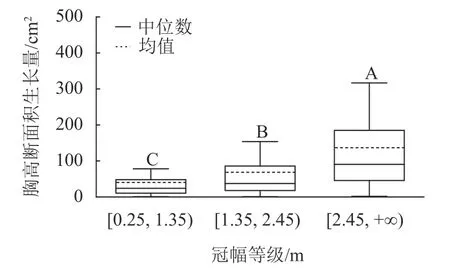
图2 不同冠幅等级的胸高断面积生长量Figure 2 Breast-height basal area increment for different crown classes

3.4 竞争对胸高断面积生长量的影响

样地林木竞争指数均值为8.44，竞争指数最小值为0.47，最大值为217.79。根据林木竞争指数均值和分布范围，将其分为3 个等级：[0, 4.00）、[4.00, 8.00）、[8.00, +∞），分别用Ⅰ竞争、Ⅱ竞争和Ⅲ竞争表示，对应3 个竞争强度等级：低度、中度、强度。不同等级的竞争指数代表林木受到的竞争压力大小不同，数值越大，竞争压力越大。对不同竞争强度等级林木的胸高断面积生长量进行K-W 非参数检验。结果显示：Ⅰ竞争、Ⅱ竞争和Ⅲ竞争林木的胸高断面积生长量的中位数分别为67.90、27.14 和29.90 cm2，H=67.434，P＜0.01，存在极显著差异；不同竞争强度等级的林木的胸高断面积生长量不同，低度竞争强度的林木胸高断面积生长量最大。用Nemenyi 法进一步证明(图3）：低度竞争与中度竞争、强度竞争林木的胸高断面积生长量呈现极显著差异(P＜0.01）。低度竞争林木的胸高断面积生长量中位数最大，说明林木受到的竞争压力越小，有利于提高林木胸高断面积生长量。

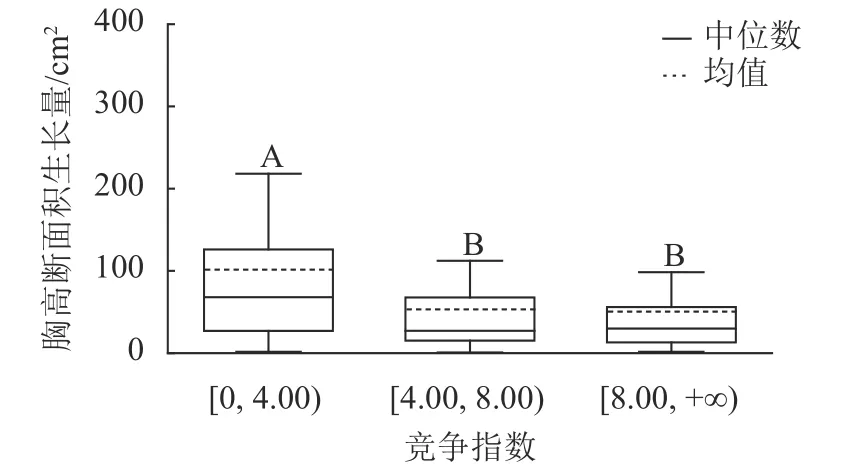
图3 不同竞争等级的胸高断面积生长量Figure 3 Breast-height basal area increment for different competition classes

3.5 单木生长模型

因为冠幅、竞争指数与胸径相关系数的绝对值均大于0.6，所以进行最小二乘回归时存在共线性问题。因此，本研究为探究胸径和竞争指数对胸高断面积生长量的影响，以式(9）为基础模型，林木胸高断面积生长量对数为因变量，冠幅、海拔、坡度和坡向指数为控制变量，分别以胸径平方、胸径对数、竞争指数和竞争指数对数的不同组合为自变量进行岭回归，得到基于单株林木的单木生长模型(表3）；对2005 年调查的林木胸径按2 cm 为组距进行径阶整化，对林木大小因子、竞争因子和立地因子计算其每一径阶的平均值，以每一径阶内林木胸高断面积生长量对数的平均值为因变量，冠幅、海拔、坡度和坡向指数等因子的平均值为控制变量，分别以每一径阶内胸径平方、胸径对数、竞争指数和竞争指数对数的平均值的不同组合为自变量进行岭回归，得到基于径阶平均值的单木生长模型(表4）。其中2 类岭回归模型的K值采用SPSSAU 给予的推荐值。

2.4.2 林木竞争因子的选取 林木竞争限制林木生长[21]。本研究选取Hegyi 竞争指数[22]及其对数形式来表示林木竞争因子的大小。其中，竞争木的选择采用汤孟平等[23]提出的基于Voronoi 图的方法。Hegyi 竞争指数的计算公式为：

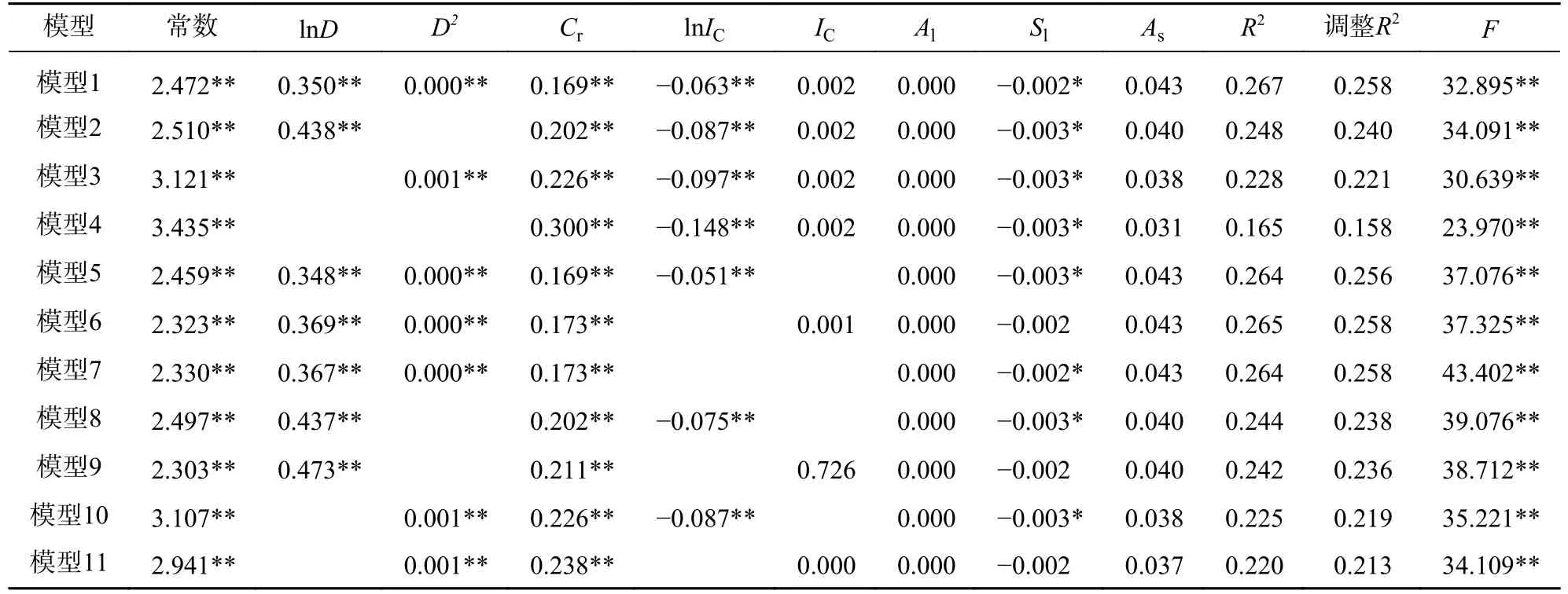
表3 基于单株林木的单木生长模型Table 3 Individual tree growth models based on individual tree

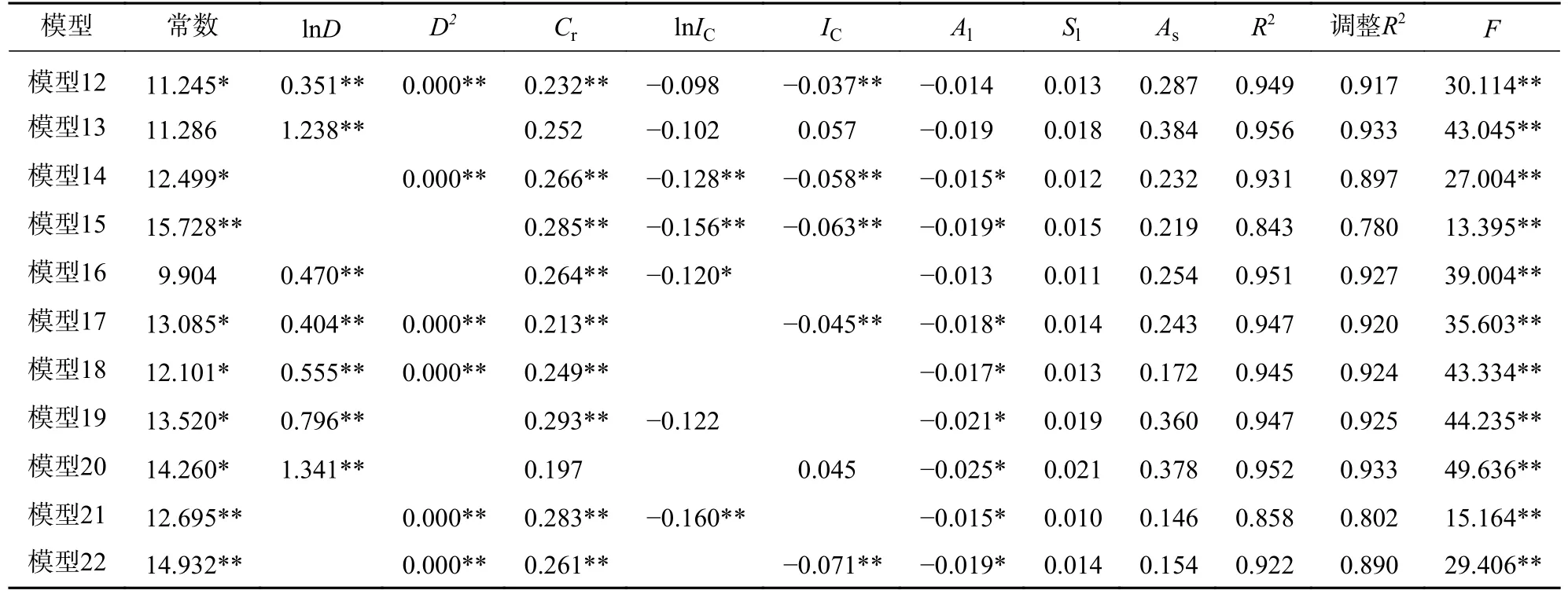
表4 基于径阶平均值的单木生长模型Table 4 Individual tree growth models based on average of diameter grade

在基于单株林木的单木生长模型中(表3），比较模型2 和模型3、模型8 和模型10、模型9 和模型11，发现含有胸径对数的模型比含有胸径平方的模型拟合精度高；比较模型1～模型4，发现含有胸径因子的模型拟合精度优于不含胸径的模型；比较模型1、模型5、模型6 和模型7，有无竞争指数对模型的拟合精度影响小；比较模型1～模型11，发现模型中常数项、胸径对数、胸径平方、冠幅和竞争指数对数的回归系数均极显著(P＜0.01），说明胸径、冠幅和竞争指数对数是单木生长模型中的重要因子；比较模型1～模型11 的R2及调整后的R2，模型1 是基于单株林木的单木生长模型中的最优模型，该模型中的常数项、胸径对数、胸径平方、冠幅、竞争指数对数和坡度等回归系数显著(P＜0.05）。

见到秘书在认真的阅读他的材料，牛皮糖连忙起身告辞，他想趁这个热劲，让秘书好好把材料读完，读进去。他知道有时候秘书的作用比书记本人还大。这时灵机一动，他把带给书记的那只黑鸡婆抓了出来，递给秘书，一脸歉意的说，秘书，对不起，来时只抓到这只鸡婆，就送给你煮汤喝吧，不成敬意，希望你收下。

釉质块样本经釉质再矿化实验和釉质脱矿抑制实验处理后，肉眼进行大体观察可见，均为C组釉质着色明显，呈棕褐色；A、B、D、E组釉质颜色无明显变化，白垩色不明显。

在基于径阶平均值的单木生长模型中(表4），比较模型13 和模型14、模型19 和模型21、模型20 和模型22，发现含有胸径对数的模型比含有胸径平方的模型拟合精度高；比较模型12～模型15，发现含有胸径因子的模型拟合精度优于不含胸径因子的模型；比较模型12、模型16、模型17 和模型18，有无竞争指数对模型的拟合精度影响小；比较模型12～模型22，发现模型中胸径对数和胸径平方的回归系数均显著(P＜0.05），说明胸径是基于径阶平均值的单木生长模型中的重要因子；比较模型12～模型22 的R2及调整后的R2，得出模型13 是基于径阶平均值单木生长模型中的最优模型，该模型中胸径对数的回归系数极显著(P＜0.01）。

比较表3 和表4 中的模型，发现2 类生长模型中胸径因子的回归系数均显著，且含有胸径因子的模型拟合精度均优于不含胸径因子的模型；基于径阶平均值的单木生长模型拟合精度高于基于单株林木的单木生长模型。

4 讨论

通过对胸径与胸高断面积生长量进行Spearman 相关分析和Kruskal-Wallis 检验，发现胸径与胸高断面积生长量呈正相关，且胸高断面积生长量随着胸径的增大而增大。该结论与多数学者的研究一致，如CHI 等[29]在研究中国神农架常绿落叶阔叶混交林的林木大小、相邻木和立地条件对林木生长的影响时发现，林木的生长量与初始胸径大小具有显著的相关关系，并且随着初始胸径的增大而增大。FIEN 等[30]对美国缅因州中部的异龄林单木生长和死亡的影响因子进行了研究，认为树种的胸高断面积与胸径均呈显著正相关。有研究表明：林木生长通常会先随胸径的增大而增加，在达到一定阶段后又会随胸径的增大而减小[31]。但也有研究指出：不同的森林类型，林木生长与胸径的关系有较大差异[32]。

竞争与胸高断面积生长量的Spearman 相关分析表明：竞争与胸高断面积生长量呈现负相关关系，低度竞争强度有助于林木生长。这个结论与前人的研究结果基本一致，de GROOTE 等[33]研究了比利时北部森林竞争对夏栎Quercusrobur、欧洲山毛榉Fagussylvatica和红槲栎Q.rubra生长的影响，指出竞争与断面积生长量呈负相关。窦啸文等[34]在研究天目山针阔混交林竞争对生长的影响时，证实林木胸高断面积生长量与Hegyi 竞争指数服从对数函数关系，且胸高断面积生长量与竞争指数显著负相关。

分析地形因子与胸高断面积生长量的相关性发现：海拔、坡向、坡度等地形因子与胸高断面积生长量的相关性较小。POMPA-GARCÍA 等[35]研究了地形对墨西哥针叶树生长的影响，指出林木基部断面积生长量随海拔的变化有显著差异，海拔1 001～1 500 m 的地区林木基部断面积生长量较高。本研究所选取的林木在同一固定样地内，海拔范围为575～677 m，地形变化不大，因此对林木生长影响较小。

本研究中竞争指数的回归系数并非都在单木生长模型达显著水平，这可能与竞争指数的选择有关。有研究表明：在选择与距离有关的竞争指数时，包含树冠因子的竞争指数优于胸径大小比值的竞争指数[31]。而本研究中冠幅因子的回归系数均在单木生长模型达到显著水平，这也验证了这一观点。但是，也有学者认为采用与距离无关的竞争指数的生长模型的拟合精度优于采用与距离相关的竞争指数的生长模型[36]。针对常绿阔叶林的生长模型，与距离无关的竞争指数是否优于与距离有关的竞争指数值得探讨。

林木生长还受光照、温度、水和土壤等因子的影响[37-41]，本研究未考虑这些因素。近些年来，有学者构建了不同树种的生长混合效应模型，发现混合效应模型的拟合精度明显优于一般模型[42-45]。因此，在进一步研究中，可构建多因子的混合效应模型，综合分析影响林木胸高断面积生长量的因素。

5 结论

通过对浙江天目山国家级自然保护区内的常绿阔叶林的林木胸高断面积生长量的影响因子进行分析，得出以下主要结论：①胸径、冠幅和竞争指数与胸高断面积生长量的相关性高，地形因子与胸高断面积生长量的相关性低。②不同径级、冠幅等级和竞争指数等级的胸高断面积生长量差异性显著。③基于径阶平均值的单木生长模型拟合精度高于基于单株林木的单木生长模型，且胸径和冠幅的回归系数均显著。④影响常绿阔叶林胸高断面积生长量的主要因子是林木胸径、冠幅和竞争指数，海拔、坡度等地形因子对胸高断面积生长量的影响不大。