百万千瓦级汽轮发电机定子线棒新型交叉换位方法研究
2023-11-03边旭孟雨鹏梁艳萍张春莉
边旭, 孟雨鹏, 梁艳萍, 张春莉
(1.哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080; 2.哈尔滨电机厂有限责任公司,黑龙江 哈尔滨 150040)
0 引 言
百万千瓦级汽轮发电机定子线棒负荷高、定子线棒截面积大,集肤效应明显,因此,定子线棒均采用多根铜线并绕的结构以减小涡流附加损耗[1-2]。但并绕股线交链的槽部以及端部漏磁场不同,导致感应电势不同,会在并绕股线之间产生很大的环流以及环流损耗,因此,并绕股线之间均采用编织换位结构。如何设计合理的定子线棒换位方法以抑制环流附加损耗是百万千瓦级汽轮发电机定子线棒设计的关键问题。百万千瓦级汽轮发电机的定子线棒通常由沿定子槽宽方向的四列并绕股线组成,为了减小发热,定子线棒采用水冷结构,因此,定子线棒既包括通电的实心铜股线又包括通水的空心不锈钢股线,复杂的定子线棒结构给换位方法的设计带来了困难。
目前,百万千瓦级汽轮发电机的定子线棒常采用双罗贝尔换位方法[3-4],即定子槽中心线两侧的两列并绕股线分别进行罗贝尔换位。为了进一步减小环流附加损耗,通常在双罗贝尔换位方法的基础上采用不足换位[5]、空换位[6]或者混合换位[6]的优化换位方法。虽然双罗贝尔换位线棒能够有效平衡由槽部漏磁场产生的环流,但由于定子槽中心线两侧的并绕股线之间不存在换位,因此,端部径向漏磁场会在定子槽中心线两侧的并绕股线之间产生很大的环流,在双罗贝尔换位方法的基础上进行优化对抑制环流附加损耗的效果有限。
目前,对定子换位线棒环流附加损耗的计算方法主要有:漏感电势法、等效电路网络法、二维多截面法以及三维有限元法。漏感电势法先通过解析公式计算每根股线的漏感电势,再计算环流损耗,虽然计算速度快,但是该方法对于漏磁场的假设过多,影响计算精度[7];等效电路网络法采用集总参数模型,股线用点来替代、换位路径用线来替代,可以快速准确得到环流附加损耗的计算结果数值,但无法给出股线漏磁、电密等分布规律,不便于分析[8];二维多截面法将三维换位模型分为多个二维截面计算,每个截面之间通过电路连接,对于槽部换位路径以及端部漏磁场的模拟过于简化[9-10];三维有限元法通过建立复杂换位结构的三维有限元模型对环流附加损耗进行计算[11-14],该方法较为准确,但是以往文献在建立有限元求解模型时,考虑网格划分以及数值计算难度,仅建立了定子单槽模型且端部渐开线结构采用分段直线等效,无法准确模拟端部漏磁场,并且对于复杂的空、实心股线换位结构,均采用实心股线换位结构等效替代,计算存有一定的误差。
本文提出一种新型交叉换位方法,给出新型交叉换位方法的降损原理以及换位结构,以一台1 055 MW汽轮发电机为例,建立定子三维全域场路耦合有限元模型,真实模拟定子线棒换位方法以及端部渐开线结构,考虑空心和实心股线的区别,对采用新型交叉换位方法的定子线棒股线电流分布以及环流附加损耗进行计算,并与传统双罗贝尔换位方法进行比较。
1 定子线棒新型交叉换位方法
本文以1 055 MW汽轮发电机为例,表1给出了该样机的主要参数,其中空心股线采用不锈钢材料,实心股线采用铜材料。

表1 电机的主要参数Table 1 Parameters of generator
1.1 降损原理
百万千瓦级汽轮发电机的定子线棒常采用双罗贝尔换位方法,即列1与列2、列3与列4分别进行槽内540°换位,如图1(a)所示。以励端位于列1的股线A和位于列4的股线D为例,换位到汽端后股线A位于列2,股线D位于列3,端部径向漏磁场在励端和汽端感生环流的方向一致互相叠加,因此,虽然该换位方法能够有效平衡槽部漏磁场产生的环流,但由于端部径向漏磁场的作用,在定子槽中心线两侧的股线之间仍产生很大的环流。新型交叉换位方法如图1(b)所示,即实心股线列1与列4、列2与列3分别进行槽内540°换位,励端位于列1的股线A换位到汽端后位于列4,励端位于列4的股线D换位到汽端后位于列1,端部径向漏磁场在励端和汽端感生环流的方向相反互相抵消,因此,通过交叉换位的方法可以有效平衡由端部径向漏磁场所产生槽中心线两侧股线之间的环流。
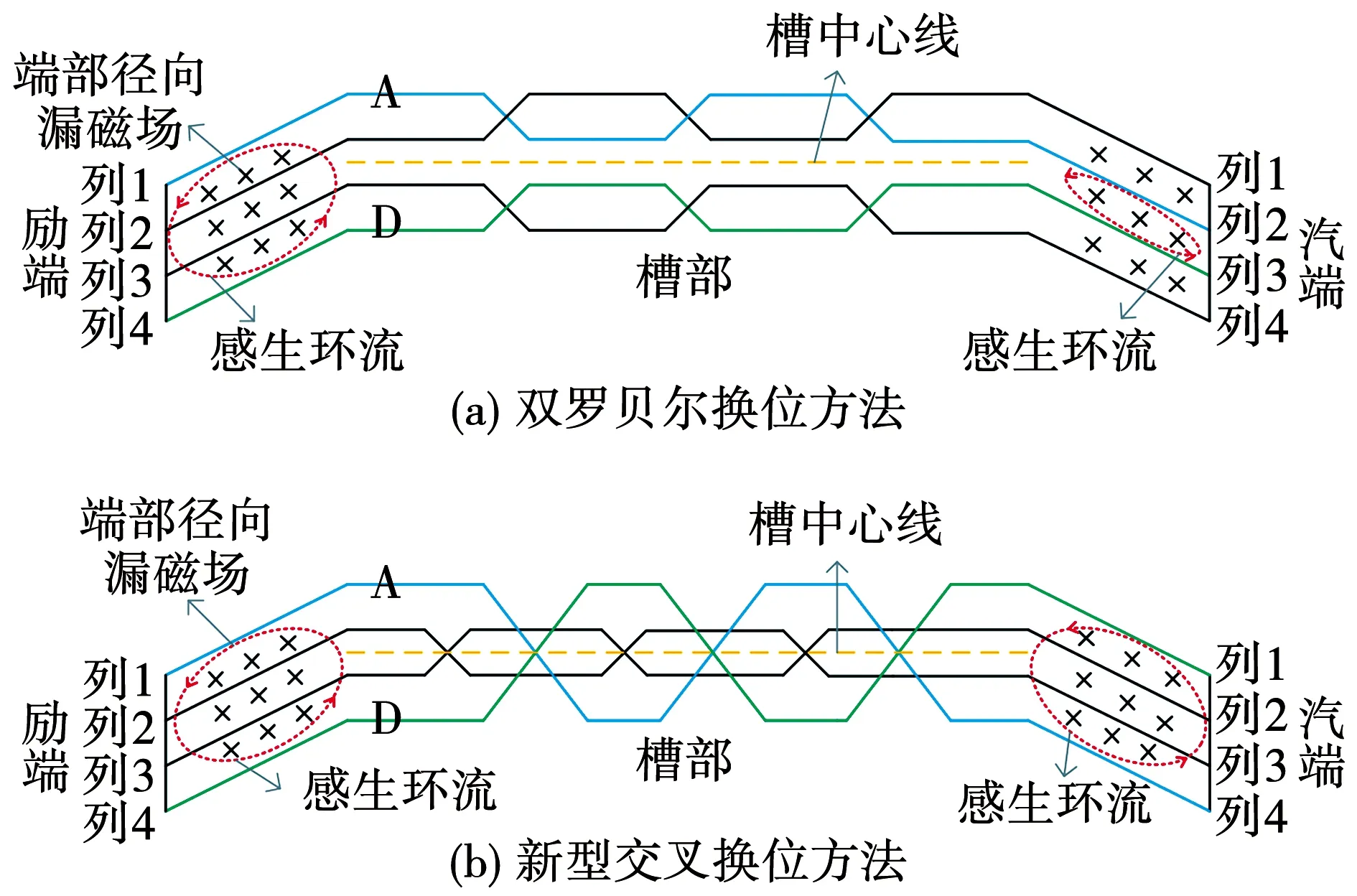
图1 两种换位方法环流示意图Fig.1 Schematic diagram of circulating current for the two transposition method
1.2 新型交叉换位结构
双罗贝尔换位方法以及新型交叉换位方法的股线编号以及换位单元如图2所示。
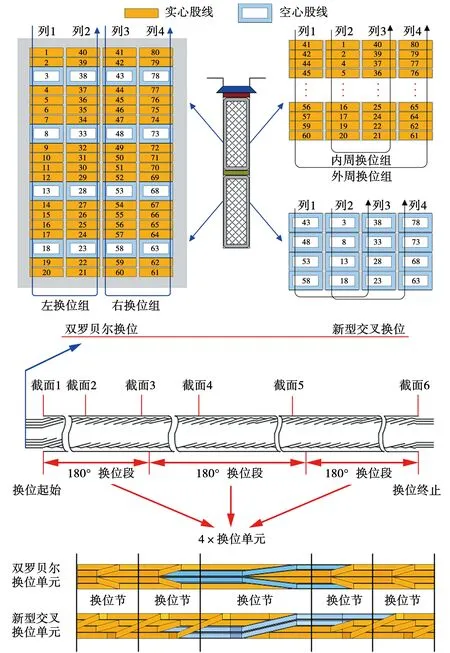
图2 两种换位方法的股线编号及换位单元Fig.2 Strand number and transposition unit for the two transposition method
双罗贝尔换位列1与列2构成左换位组,列3与列4构成右换位组。新型交叉换位方法实心股线列1与列4构成外周换位组,列2与列3构成内周换位组;空心股线列1与列3、列2与列4分别构成换位组。两种换位方法均采用槽内540°换位,由3段180°换位段组成,前、后两个换位段的长度相同,中间换位段的长度与前、后两个换位段长度之和相同。每个180°换位段均由4个换位单元组成,每个换位单元由5个换位节组成,双罗贝尔换位方法的左、右换位组在轴向上的相同位置进行换位,新型交叉换位的外、内周换位组在轴向上不同位置进行换位。
两种换位方法的结构示意图如图3所示。新型交叉换位的外周换位组轴向延后一段距离换位,使得外周换位组的抬起最高点恰好在内周换位组的换位弯处。延后换位使得定子线棒的总高度与双罗贝尔线棒的总高度一致,避免了外、内周换位组同时换位导致线棒过高、局部过热的问题;同时空心股线选择统一的换位结构,使得不易轧制的不锈钢管仅呈现一种扭转状态,易于工程制造。

图3 两种换位方法结构示意图Fig.3 Schematic diagram of structure for the two transposition method
2 环流附加损耗计算方法
2.1 基本假设
采用三维场路耦合有限元法进行环流附加损耗计算,作如下基本假设:
1)由于百万千瓦级汽轮发电机气隙较大,而且定子槽楔、楔下垫条以及主绝缘的存在,使得定子线棒距离槽口较远,可以忽略转子主极磁场的影响,图4为计算得到的样机在空载工况下的槽部漏磁场分布以及上层线棒的磁密,主极磁场几乎不会影响上层线棒位置的漏磁,证明了假设的合理性。
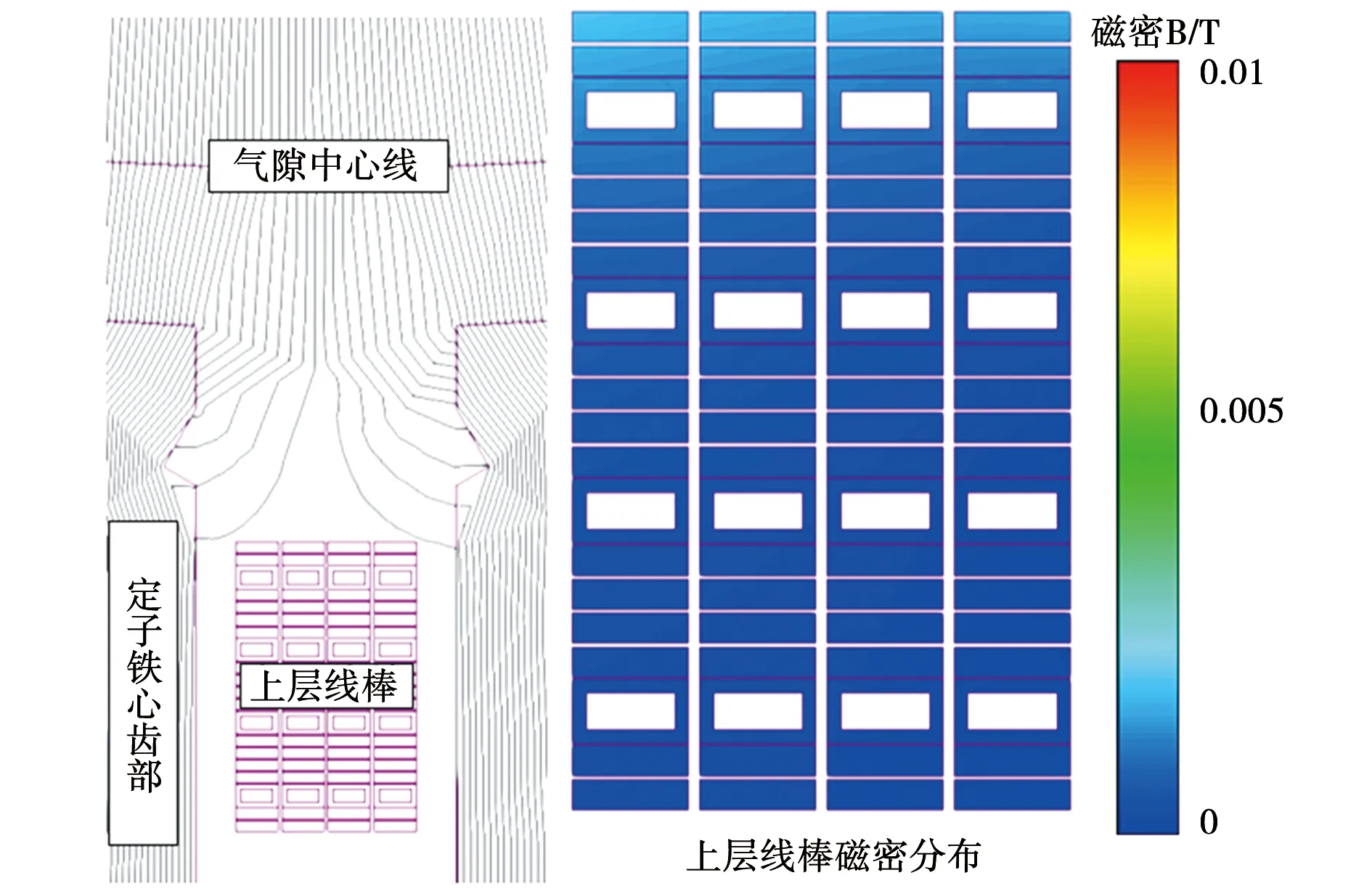
图4 空载工况下上层线棒磁场分布Fig.4 Magnetic flux distribution of the top layer bar under no-load condition
2)忽略磁场中的位移电流及高次谐波,默认所有场量均为正弦波。
3)不考虑定子铁心材料磁饱和。
4)为了减少计算所用内存和提高求解速度,端部整体渐开线模型采用分段渐开线模型等效,将端部渐开线曲线分为六段,每一段分别按照渐开线实际结构建模,如图5所示。

图5 端部渐开线等效结构Fig.5 Equivalent structure of the end involute
2.2 计算模型
根据汽轮发电机定子结构,建立定子三维全域场路耦合求解模型。三维磁场计算模型与新型交叉换位股线的剖分网格如图6所示,模型包括定子铁心、定子线棒以及空气域,考虑计算资源,仅一个定子槽内的上、下层线棒按照实际分股换位结构建模,定义为换位槽,其余定子槽内的上、下层线棒均按整块导体建模,不考虑导体的涡流效应。

图6 三维磁场计算模型Fig.6 Solving model of 3D magnetic field
采用三维时谐场对磁场计算模型进行求解,满足的磁场计算方程为:
(1)
三维磁场计算模型的外边界条件为:
(2)
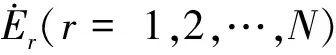
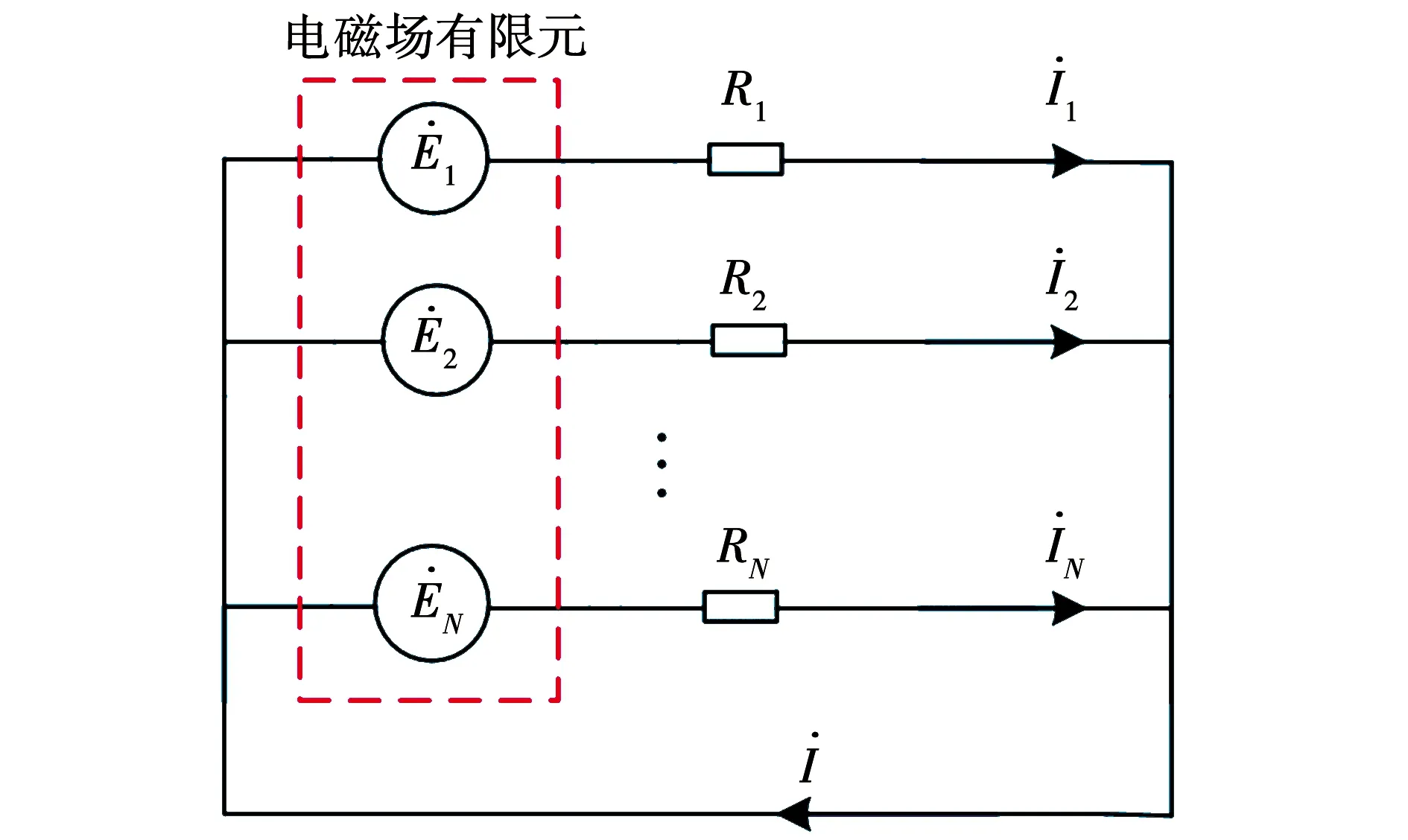
图7 单根换位线棒场路耦合模型Fig.7 Field circuit coupled model of transposition bar
单根换位线棒的电路方程如式(3)所示,电磁场与电路方程通过单根股线的感应电动势进行耦合。
(3)
2.3 环流附加损耗计算

(4)
3 新型交叉换位方法与传统双罗贝尔换位方法对比分析
3.1 电密对比分析
为了对比两种换位方法的电密分布情况,从汽端到励端选取6个截面,所选截面位置如图2所示。两种换位方法的上、下层电密分布对比如图8和图9所示。可以看出,两种换位方法的电密大小分布呈现较为明显的规律性,上下层线棒的电密分布几乎一致,且随着股线的换位,电密分布也在发生变化,传统的双罗贝尔换位方法左换位组的电密大小要明显小于右换位组,新型交叉换位的电密分布较为均匀,双罗贝尔换位线棒的上层股线电密最大值为1.51×107A/m2、下层股线电密最大值为1.58×107A/m2,新型交叉换位的上层股线电密最大值为1.50×107A/m2、下层股线电密最大值为1.48×107A/m2。
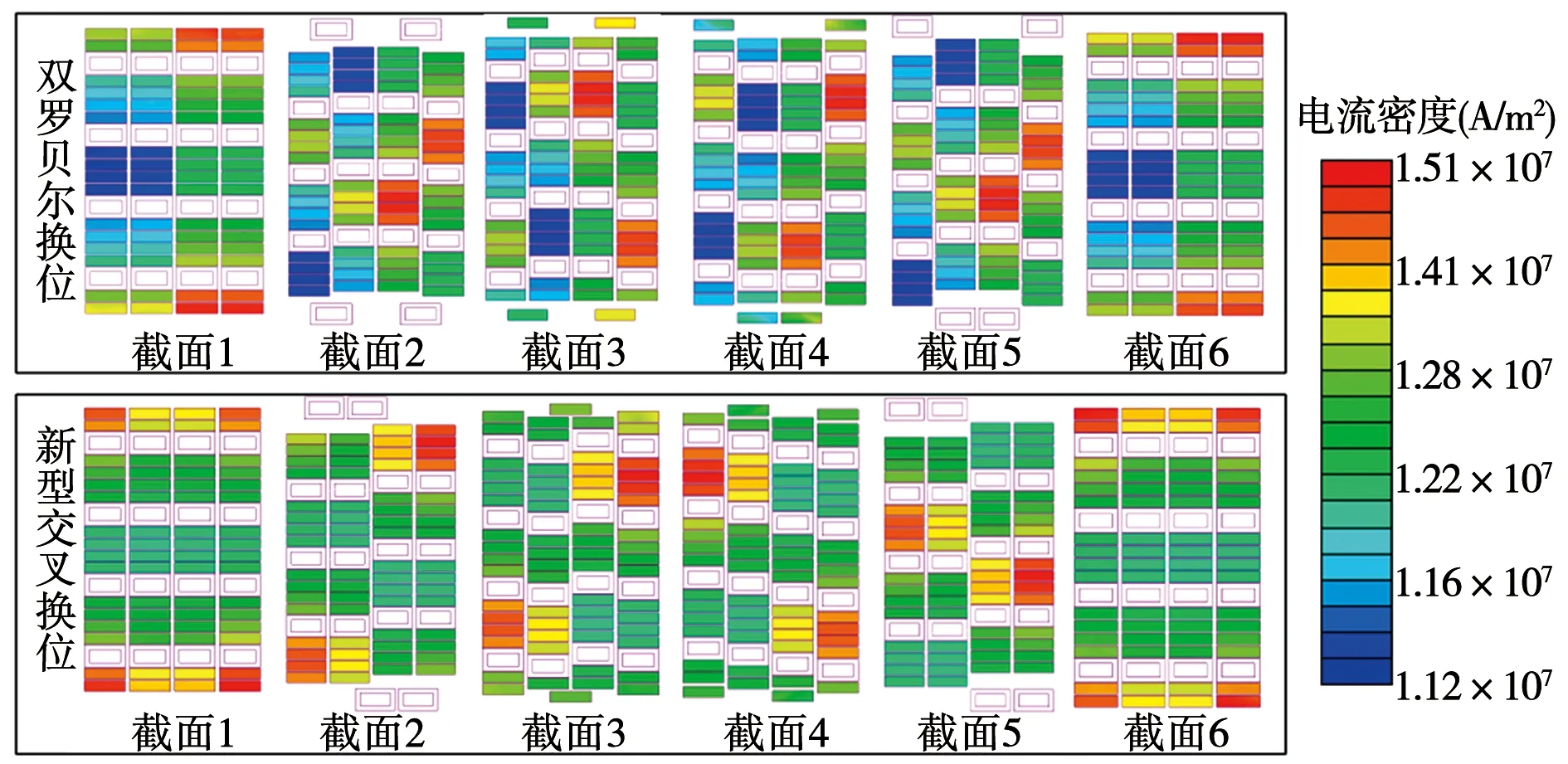
图8 两种换位方法上层股线电密云图Fig.8 Current density of the top layer strands for two transposition methods

图9 两种换位方法下层股线电密云图Fig.9 Current density of the bottom layer strands for two transposition methods
3.2 股线电流分布对比分析
两种换位方法股线电流分布对比如图10所示,由于传统双罗贝尔换位的两个换位组之间未构成换位路径,导致股线未能均匀地占据槽内空间,从而出现换位组间的环流。计算模型的上下层处于同相槽,且换位方式一样,所以下层线棒的股线电流分布与上层线棒趋势相同。新型交叉换位的换位方法抵消了端部径向漏磁场的影响,使得感生环流较小,股线电流分布较为均匀。
3.3 环流损耗对比分析
传统双罗贝尔换位方法和新型交叉换位方法的换位槽上、下层线棒的环流损耗对比如表2所示,采用新型交叉换位方法的环流总损耗与传统双罗贝尔换位相比,减少了31.5%,表明采用本文提出的换位方法可以有效减少环流损耗,有利于发电机的平稳运行。

表2 定子线棒环流损耗Table 2 Circulating current losses of stator bars kW
3.4 结果验证
目前,针对百万千瓦级的汽轮发电机,定子换位线棒难以通过试验直接测得环流损耗的大小,因此采用与本文有限元法计算原理不同的等效电路网络法[4]进行验证,该方法建立定子换位线棒的等效电路网络模型,以“离散积分”为基本思想计算模型中的漏电抗参数。两种方法计算得到的采用新型交叉换位方法的上、下层股线电流对比如图11所示。
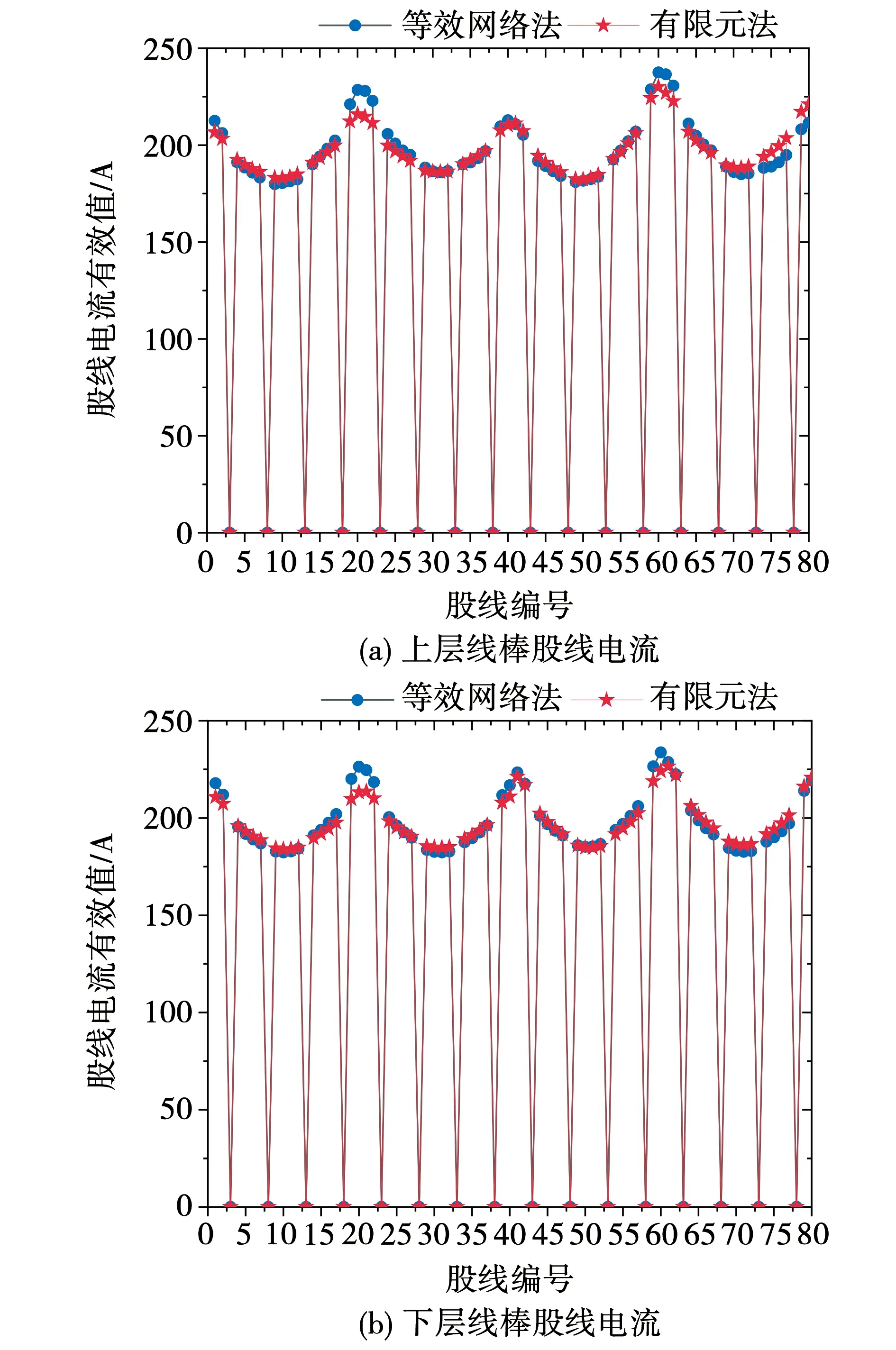
图11 两种计算方法股线电流结果对比Fig.11 Strand current comparison between two calculation methods
可以看出,对于新型交叉换位线棒,两种计算方法所得结果趋势吻合,单根股线电流最大相对误差为5.8%,可以验证本文三维全域场路耦合有限元计算结果的正确性。
4 结 论
本文以一台1 055 MW汽轮发电机为例,建立了定子换位线棒的三维全域场路耦合有限元计算模型,研究了不同换位方法对股线环流的影响,通过与解析法的结果对比验证了该建模方法的正确性,得出以下结论:
1)提出了一种新型交叉换位方法,实心股线列2与列3换位、列1与列4延后一段距离进行换位,空心股线列1与列3、列2与列4换位,既可以抵消端部径向漏磁场产生的环流,又可以使得定子线棒的总高度与双罗贝尔线棒的总高度一致,避免了两个换位组同时换位导致线棒过高的问题,可以提高发电机的运行效率。
2)与传统双罗贝尔换位方法相比,新型交叉换位的股线电流分布更加均匀,且单根股线电密最大值降低。采用双罗贝尔换位方法时换位槽内上、下层定子线棒的总环流附加损耗为3.336 kW,采用新型交叉换位方法时为2.284 kW,降低了31.5%。
