扩展卡尔曼滤波参数辨识下永磁同步电机模型预测转矩控制
2023-11-03李洪凤徐浩博徐越
李洪凤, 徐浩博, 徐越
(天津大学 电气自动化与信息工程学院,天津 300072)
0 引 言
永磁同步电机(permanent magnet synchronous motor,PMSM)具有结构简单、功率密度高、效率高等优点,在电梯牵引、精密机床、航空航天等领域得到了广泛的应用[1-3]。近年来,模型预测转矩控制作为一种新型的控制方式,能够显著提升电机转矩的动态性能,被广泛应用于永磁同步电机系统中[4]。
传统的模型预测转矩控制通过构建转矩和磁链的价值函数,采用电压矢量穷举法对价值函数进行滚动寻优[4]。为了提升电机的稳态性能,需要增加备选电压矢量,这样势必会大大增加计算负担。而且,价值函数中,磁链误差和转矩误差之间存在权重系数整定问题,权重系数的整定多半采用试凑法[5-6]。而无差拍预测控制策略通过对转矩和定子磁链进行无差拍预测,来求解出参考电压矢量,无需穷举法对价值函数进行寻优,从而减轻了计算负担。文献[7]对转子和定子磁链使用无差拍控制后,使用占空比算法进行调制,而文献[8]则在进行无差拍控制后,直接将传统穷举方法的8次减小到2次,并直接单矢量输出,这两种方式的转矩脉动仍然较大,可以进行改善。为了提高稳态性能,文献[9]提出一种双矢量无差拍模型预测转矩控制,将转矩和磁链表示的价值函数转化为由电压表示的价值函数,通过对电压矢量寻优,得到距离参考电压矢量最近的电压双矢量组合。但是其中的双矢量组合寻优算法较为复杂。本文将由转矩和磁链的价值函数转化为电压参考矢量,然后将得到的电压参考矢量直接送入空间矢量脉宽调制(space vector pulse width modulation,SVPWM)模块,算法简单易实现,且稳态性能好。
基于无差拍预测得到的参考电压矢量对电机参数具有较强的依赖性,当实际电机参数受到温升、磁场饱和等因素影响而发生变化时,会使得转矩和磁链产生预测误差,使控制性能变差[10]。其中电阻失配会使得给定转矩和实际转矩之间出现静差,电感失配会使得系统稳定性变差。而在无差拍模型预测转矩控制中,电阻电感参数失配会使得输入到逆变器中的控制电压发生明显畸变,极大影响了控制效果。
参数辨识是通过系统的输入输出来辨识电机参数,将参数准确值再代入预测模型中,消除由于参数扰动带来的预测误差,保证系统的稳定运行。目前常用的在线辨识算法主要包括模型参考自适应、最小二乘法、扩展卡尔曼滤波等。文献[11]通过最小二乘法在线辨识电阻和电感,以消除电阻和电感参数失配对预测控制效果的影响。文献[12]采用模型参考自适应同时辨识永磁同步电机的电感和磁链参数,并将辨识出的参数值实时反馈至电流预测控制器中。文献[13]提出一种基于递推最小二乘法的内置式永磁同步电机多参数在线估计方法。文献[14-15]使用扩展卡尔曼滤波器对磁链参数进行辨识,提升了磁链参数的鲁棒性。在上述方法中,模型参考自适应对噪声敏感,最小二乘法容易出现数据饱和现象,而扩展卡尔曼滤波是一种适用于非线性时变系统的最优递推估计算法。其能够同时辨识电机的参数和状态,克服参数辨识中的噪声敏感问题,适用于传感器受噪声影响的系统。本文采用扩展卡尔曼滤波进行在线参数辨识,有助于提升控制系统的鲁棒性。
本文提出基于扩展卡尔曼滤波的无差拍预测转矩控制策略,首先使用无差拍预测,对转矩和磁链的追踪转变为对参考电压矢量的追踪,在得到参考电压矢量后使用SVPWM调制,从而提升系统的稳态性能。此外,为了提升模型参数鲁棒性,使用电流预测方程作为状态方程,利用扩展卡尔曼滤波器对电阻和电感在线辨识并在模型中实时更新,提升算法的参数鲁棒性。
1 永磁同步电机数学模型
1.1 dq坐标系下PMSM的数学模型
本文使用表贴式永磁同步电机(surface-mounted permanent magnet synchronous motor,SPMSM),其三相绕组空间对称,不考虑铁心损耗的情况下,在dq轴坐标系下的电压方程为:
(1)
磁链方程为:
(2)
式中:id和iq为dq轴下的定子电流;ud和uq为dq轴下的定子电压;ψd和ψq为dq轴下的磁链;ωe为电角速度;R为定子电阻;ψf为永磁体磁链;SPMSM的d轴电感和q轴电感相等,即Ld=Lq=L。
电磁转矩方程为
(3)
式中p为SPMSM极对数。
对式(1)进行离散化处理,从而得到下一时刻的磁链预测值为:
(4)
式中:id(k)和iq(k)为kTs时刻的dq轴定子电流;ud(k)和uq(k)为kTs时刻的dq轴定子电压;ψd(k)和ψq(k)为kTs时刻的dq轴磁链;ψd(k+1)和ψq(k+1)为(k+1)Ts时刻的dq轴磁链;Ts为控制周期。
下一时刻的转矩预测值为
(5)
式中:iq(k+1)为(k+1)Ts时刻的电流预测值;Te(k+1)为(k+1)Ts时刻的转矩预测值。
1.2 延时补偿
由于在数字化实现方式中,计算和采样会占用时间,选出的最优矢量在下一控制周期才能作用于电机上,使系统性能变差,所以需要对电流进行延时补偿,即:
(6)
从而可以得到(k+2)Ts时刻的预测电流、磁链和转矩值,即:
(7)
iq(k+1)R-Lωeid(k+1)-ωeψf];
(8)
(9)
2 无差拍模型预测转矩控制
2.1 无差拍预测控制原理
根据dq轴下的磁链方程式(2),(k+2)Ts时刻的磁链预测值可以表示为:
(10)
且磁链预测值满足:
(11)
由式(9)解出iq(k+2),然后代入式(10),可以得到(k+2)Ts时刻的q轴磁链预测值为
(12)
将式(12)代入式(11),可以得到(k+2)Ts时刻的d轴磁链预测值为
(13)

(14)

图1 永磁同步电机磁链矢量关系Fig.1 Flux vectors relationship of permanent magnet synchronous motor

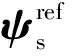
由式(7)可得:
(15)

(16)
使用SVPWM的调制方式,存在相位延迟现象,这是由于在计算时采用的是第k+1时刻的转子位置角θ(k+1),而实际过程中的电压作用时,转子位置角由θ(k+1)变为θ(k+2),因此坐标变换带来了相位延迟现象,需要进行补偿,相位延迟示意图如图2所示。
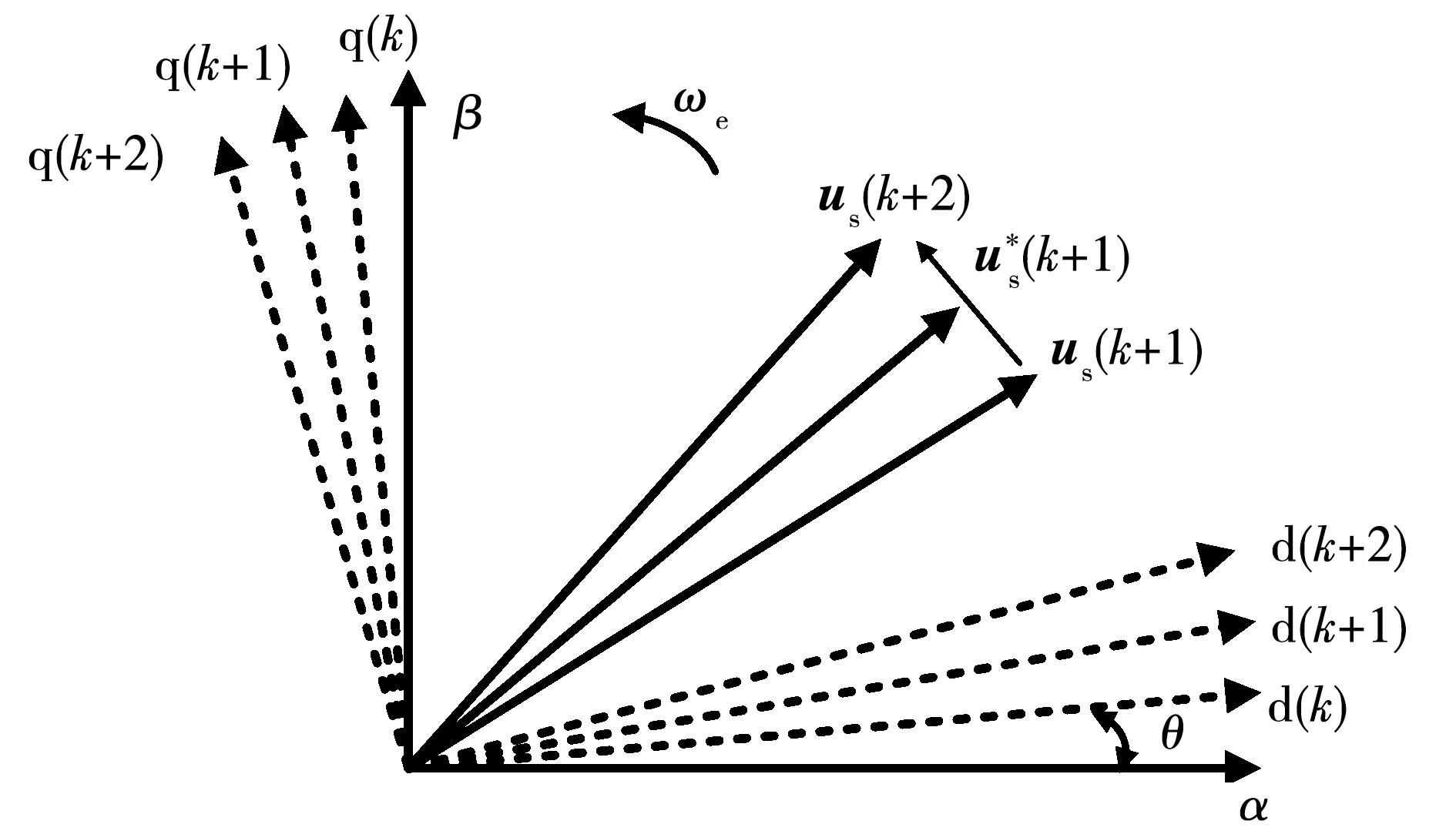
图2 相位延迟示意图Fig.2 Schematic diagram of phase delay
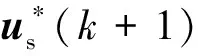
(17)
相位延迟具体的实现过程如图3所示。
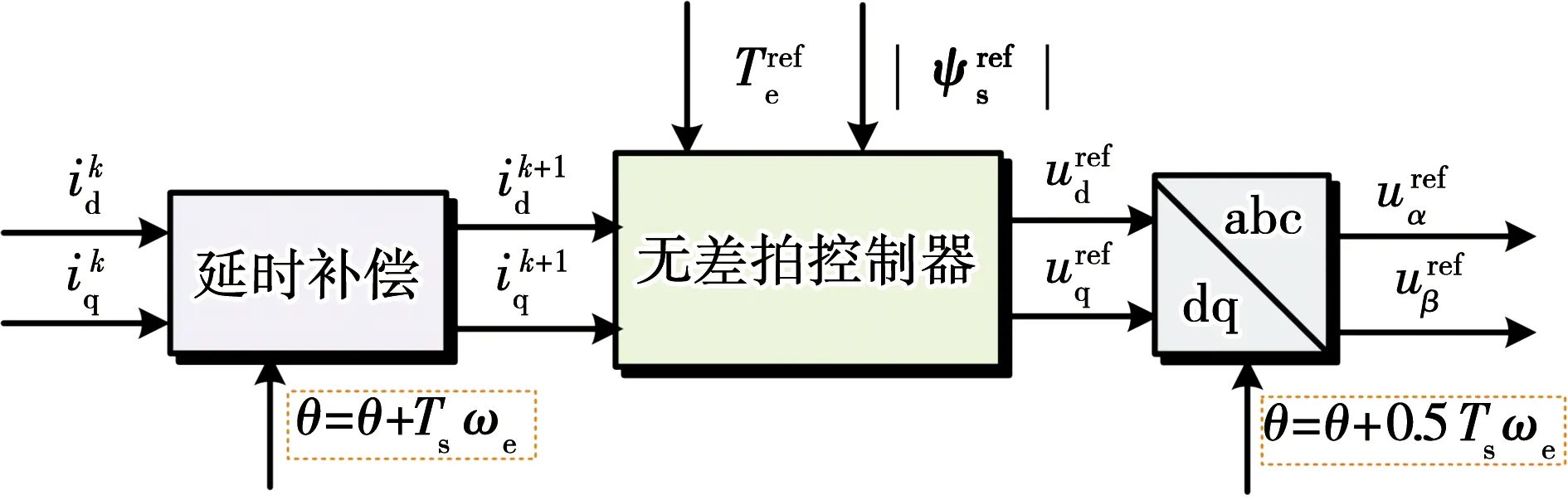
图3 相位延迟示意图Fig.3 Schematic diagram of phase delay
2.2 定子电阻与电感对控制效果的影响
为了简化推导过程,不考虑延时补偿的情况。由式(2)与式(16)可得:
(18)
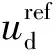
当仅存在定子电阻参数失配时,电机实际输出量为:
(19)
电机输出量误差为:
(20)
由于采用id=0控制策略,因此d轴输出电压与定子电阻误差无关。q轴输出电压误差与负载和定子电阻误差有关,且负载一定时,q轴输出电压误差与定子电阻误差成正比。
当仅存在定子电感参数失配时,电机实际输出量为:
(21)
电机输出误差为:
(22)
由于采用id=0控制策略,因此d轴输出电压误差与转速、负载、定子电感误差有关。q轴输出电压误差与负载、定子电感误差有关,且负载一定时,q轴输出电压误差与定子电感误差成正比。
因此,无差拍模型预测转矩控制的控制效果与定子转子参数取值是否准确密切相关。
2.3 定子电阻与电感的扩展卡尔曼滤波辨识
为提升控制策略的参数鲁棒性,在实际电机参数发生改变时仍然拥有良好的控制性能。本文采用扩展卡尔曼滤波(extended Kalman filter,EKF)来提升控制策略的参数鲁棒性。
非线性的离散系统状态方程可以表示为:
(23)
式中:xk和xk-1为当前及上一时刻的系统状态量;uk-1为输入量;wk-1为系统输入噪声;yk为系统输出量;vk为测量噪声。
EKF的本质是最小均方误差意义下的最优估计,其迭代过程分为两步。
(24)
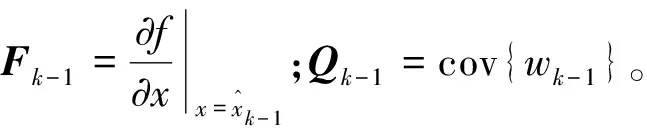
2) Permanent magnet synchronous electricity generation system
第二步为修正过程,表达式为:
(25)


将电压方程作为状态方程,由于定子电阻R和电感L存在耦合,故定义中间变量为:
(26)
在永磁同步电机的无差拍预测转矩控制中,其控制周期通常较短,此时可以认为定子电阻R和电感L在一个控制周期内不发生变化,即中间变量在一个控制周期内也不发生变化,并将中间变量代入预测方程中,可以构建离散形式的EKF状态方程为:
(27)
由式(27)选取状态变量矩阵为xk=[id(k)iq(k)a(k)b(k)]T,输出变量矩阵yk=[id(k)iq(k)]T,其雅克比矩阵为
(28)
测量矩阵为
(29)
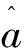
(30)
本文所提算法将辨识出的电阻和电感参数反馈至无差拍预测转矩模型中,避免了模型参数和实际电机参数失配带来的影响,提升了参数鲁棒性,本文所提控制策略原理结构框图如图5所示。
3 仿真与实验验证
本节使用仿真和实验对所提算法进行验证,并与参数失配下的情况进行比较,永磁同步电机仿真与实验参数如表1所示,控制频率使用Ts=200 μs。
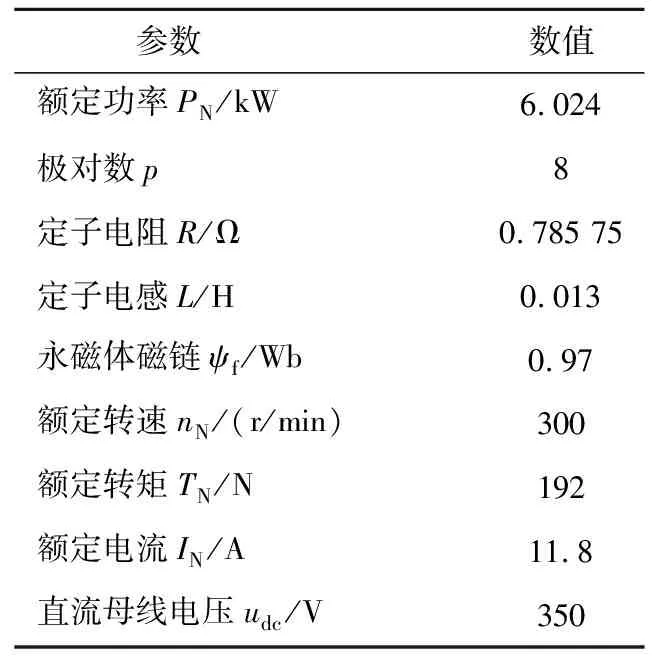
表1 永磁同步电机仿真与实验参数
3.1 仿真验证
为了讨论延时补偿对本文所提算法的影响,文中对有无延时补偿情况下,电感和电阻的辨识结果进行对比分析。不考虑延时补偿的情况下,电机电感与电阻辨识结果如图6所示。电机定子电感实际值为13 mH,电感辨识结果为13.78 mH,辨识误差为6%。电阻实际值为0.785 75 Ω,电阻辨识结果为0.788 73 Ω,辨识误差为0.38%。
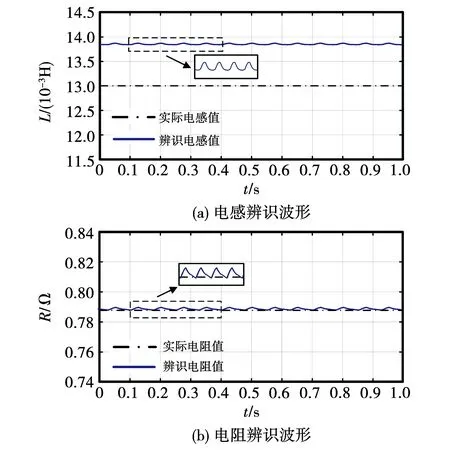
图6 未考虑延时补偿情况下本文所提算法辨识波形Fig.6 Waveform identification of the proposed algorithm without considering delay compensation
图7给出了考虑延时补偿情况下,本文所提控制策略辨识的电感和电阻波形。电感辨识结果为13.02 mH,辨识误差为0.154%。电阻实际值为0.785 75 Ω,电阻辨识结果为0.788 78 Ω,辨识误差为0.39%。

图7 考虑延时补偿情况下本文所提算法辨识波形Fig.7 Waveform identification of the proposed algorithm considering delay compensation
综上可以看出,考虑延时补偿的辨识结果更为准确。
为了验证本文所提算法的有效性,在电机标幺电阻、电感参数下,对本文所提算法与传统模型预测转矩控制算法的控制效果进行对比分析。仿真设置永磁同步电机转速为50 r/min,负载转矩为额定转矩192 N·m。图8为电机在此工况下的A相定子电流、电磁转矩与定子磁链波形。
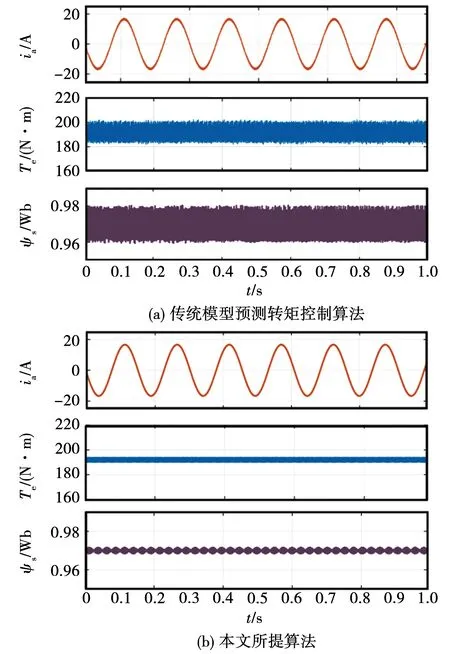
图8 参数未失配情况下传统算法与本文所提算法稳态性能Fig.8 Steady-state performance of traditional algorithm and the proposed algorithm in the case of no parameter mismatch
由图8可以看出,本文所提算法得到的电磁转矩与定子磁链的脉动较传统算法明显减小。对A相定子电流采用谐波分析(total harmonic distortion, THD)。两种算法THD值分别为3.58与1.89,本文所提算法的电流畸变程度较小。综上,由本文所提算法得到的电机电磁转矩、定子磁链及定子电流均明显优于传统算法,从而验证了本文所提算法的有效性。
对于电机运行工况中存在的参数失配条件问题,文献[16]对电机不同工况下,电机参数的变化进行了分析。该文献提到磁路饱和是影响电机电感参数变化的一项关键因素,当定子铁磁材料承受高磁场作用时,铁磁材料的磁导率将发生非线性变化。并通过理论推导得出高磁场作用会导致定子电感变化超过200%。文献[17]分析了温度对定子电阻参数的影响,在电动汽车等一些对电机功率密度要求比较高的领域中,电机温度变化范围较大,定子电阻将会出现40%左右的变化。文献[18]指出,当定子电阻温度升高时,阻值可由0.133 Ω上升至0.183 Ω,上升比率为37.5%。本文将参数失配条件定为电阻失配5倍,电感失配2.5倍,参数失配条件参阅了文献[19]。由式(20)分析可知,当采用id=0控制策略时,d轴输出电压与定子电阻误差无关,q轴输出电压误差与定子电阻误差成正比。在电阻失配度较低时,电机的实验结果差异性在图形表现上不是很明显,因此,为了直观表现电阻失配对电机性能的影响,本文对失配条件进行了夸大处理。本文所提的参数辨识策略既可以在一定程度上提高电机的参数鲁棒性,又可以为电机的早期故障提供诊断信息。
仿真设置永磁同步电机的转速为100 r/min,负载转矩为80 N·m,图9给出了参数失配情况下(电阻失配5倍和电感失配2.5倍),在有、无参数辨识环节情况下,电机的稳态性能,包括相电流、电磁转矩和磁链波形的对比分析。
由图9(a)可以看出,当电阻失配5倍时,给定转矩和实际转矩之间出现静差,给定转矩值下移,这是由于电阻失配从而带来了转矩预测误差。由图9(b)可以看出,当电感失配2.5倍时,转矩出现震荡现象,给定转矩不能准确跟随实际转矩,磁链的波动变大,这是由于电感失配不仅会带来转矩预测误差和磁链预测误差,此外,在电感失配程度较高时,会使系统稳定性受到影响。由图9(c)可以看出,由于本文所提算法使用的电阻和电感通过在线辨识而来,所以稳态性能良好。
为了量化表示电阻失配5倍时,有、无参数辨识环节情况下的实际转矩和给定转矩的偏移程度,定义
(31)
样本数据N=100 000,量化结果如表2所示。可以看出,无参数辨识环节时,电阻失配5倍情况下,实际转矩和给定转矩之间发生了严重的偏移。而有参数辨识情况下,稳态性能良好。

表2 100 r/min,80 N·m时有无参数辨识环节时稳态性能量化结果
图10给出了电感失配2.5倍时,有、无参数辨识环节情况下的电流THD分析。可以看出,存在参数辨识环节时,电感失配2.5倍电流的谐波含量不大,不存在参数辨识环节时,电感失配2.5倍电流的谐波含量增大,系统稳定性变差。
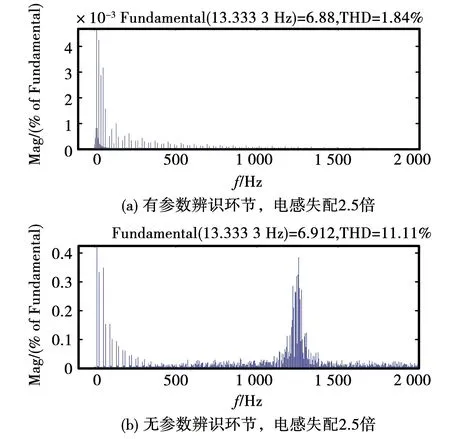
图10 有无参数辨识环节时电流THD分析Fig.10 THD analysis of current with or without parameter identification link
为了验证本文所提控制策略的动态性能,仿真设置在转速50 r/min,在0.5 s时,负载转矩由50 N·m突变至65 N·m。图11给出了本文所提控制策略的相电流、电磁转矩和磁链的仿真动态波形。可以看出,在转矩突变的情况下,本文所提控制策略的转矩能够快速进行跟随,具有良好的动态性能。
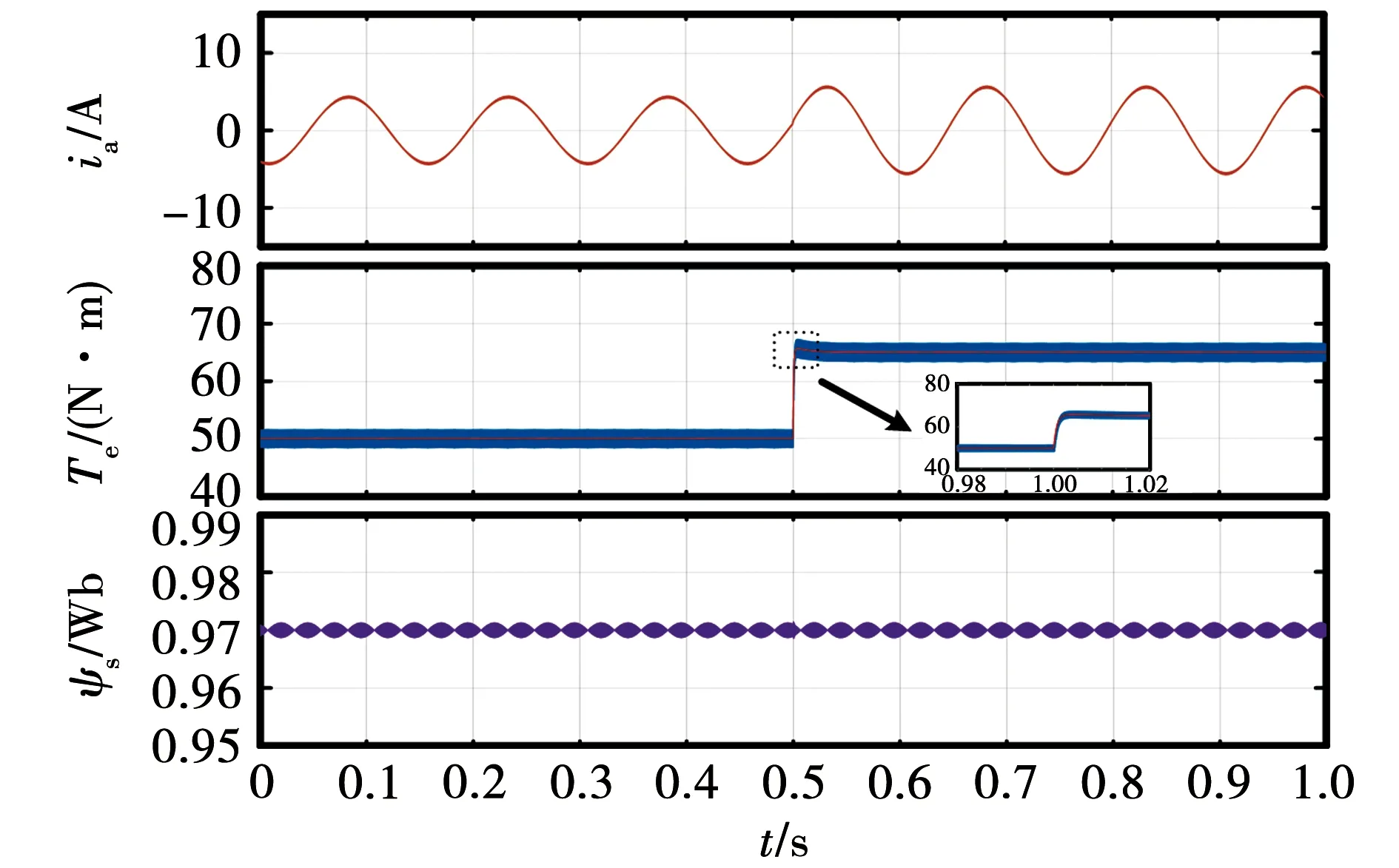
图11 本文所提算法动态波形Fig.11 Dynamic waveform of the algorithm proposed
3.2 实验验证
本文在一台6 kW的永磁同步电机上进行了实验。控制器采用TI公司的浮点微处理器TMS320F28335构成,PMSM控制系统由控制电路和功率电路组成,负载为SINAMICS的S120控制的11.2 kW感应电机,实验平台如图12所示。
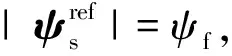
当电机温度上升时,实际电阻值也会增加,电机在实际运行过程当中也会发生电感值变大的现象,图13对比了参数失配情况下(电阻失配5倍和电感失配2.5倍),在有、无参数辨识环节情况下电机稳态性能,包括相电流、电磁转矩和磁链波形。
由图13(a)可以看出,当电阻失配5倍时,电流和磁链波形几乎没有变化,参考转矩向下偏移,这是由于电阻失配时会产生转矩的预测误差。由图13(b)可以看出,当电感失配2.5倍时,参考转矩向上偏移,实际磁链向下偏移,这是由于电感失配时会产生转矩预测误差与磁链预测误差,此外转矩和磁链的波动变大,这是由于电感失配会使得系统的稳定性变差。由图13(c)可以看出,由于本文所提算法使用的电阻值和电感值由在线辨识而来,并实时反馈至模型中,所以在参数失配的情况下,仍具有良好的稳态性能。
表3为使用Merror量化表示电阻失配5倍时,有无参数辨识环节时的稳态性能,样本N=100 000。可以看出,无参数辨识环节时,电阻失配5倍情况下,实际转矩和给定转矩之间发生了严重的偏移。而有参数辨识情况下,稳态性能良好。

表3 100 r/min,80 N·m时有无参数辨识环节时稳态性能量化结果
图14给出了电感失配2.5倍时,有、无参数辨识环节情况下的电流THD分析。可以看出,存在参数辨识环节时,电感失配2.5倍电流的谐波含量为10.16%,不存在参数辨识环节时,电感失配2.5倍电流的谐波含量增大为15.24%,系统稳定性变差。
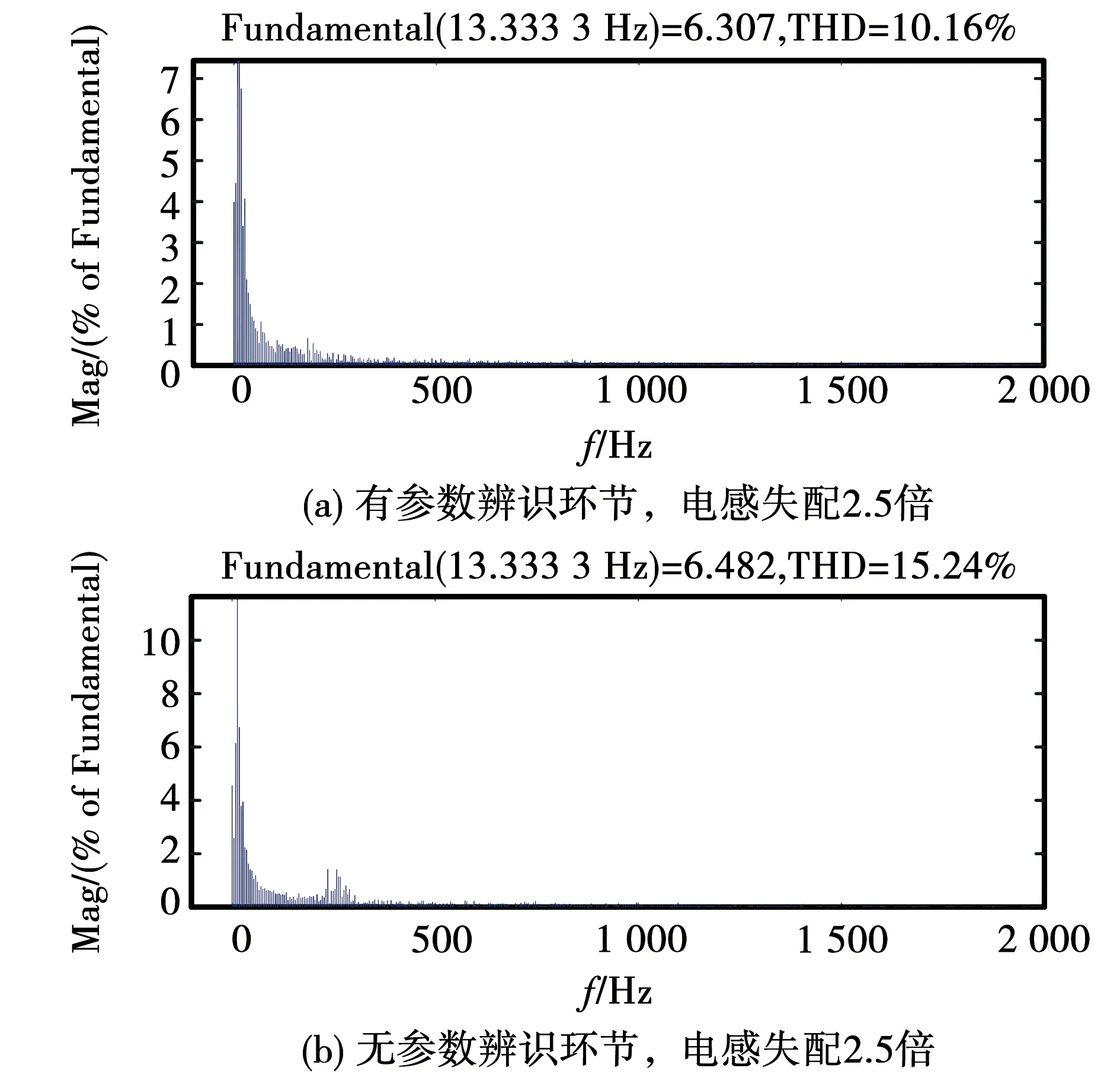
图14 有无参数辨识环节时电流THD分析Fig.14 THD analysis of current with or without parameter identification link
表4为使用Merror量化表示电感失配2.5倍时,有无参数辨识环节时的电感与磁链的脉动情况,样本N=100 000。可以看出,在有参数辨识环节时,电感失配2.5倍情况下,转矩和磁链的脉动均比无参数辨识环节时小,说明本文所提算法中加入参数辨识环节具有优越性。

表4 100 r/min,80 N·m时有无参数辨识环节时稳态性能量化结果
为了验证本文所提算法的动态性能,实验设置转速为50 r/min,在2.5 s时,负载转矩由50 N·m突变至65 N·m。图15给出了本文所提控制策略的相电流、电磁转矩和磁链的实验动态波形。可以看出,当转矩突变时,本文所提算法的转矩波形能够迅速响应,具有良好的动态性能,实验动态性能相较仿真动态性能较慢的原因是实验中电机存在阻尼摩擦。
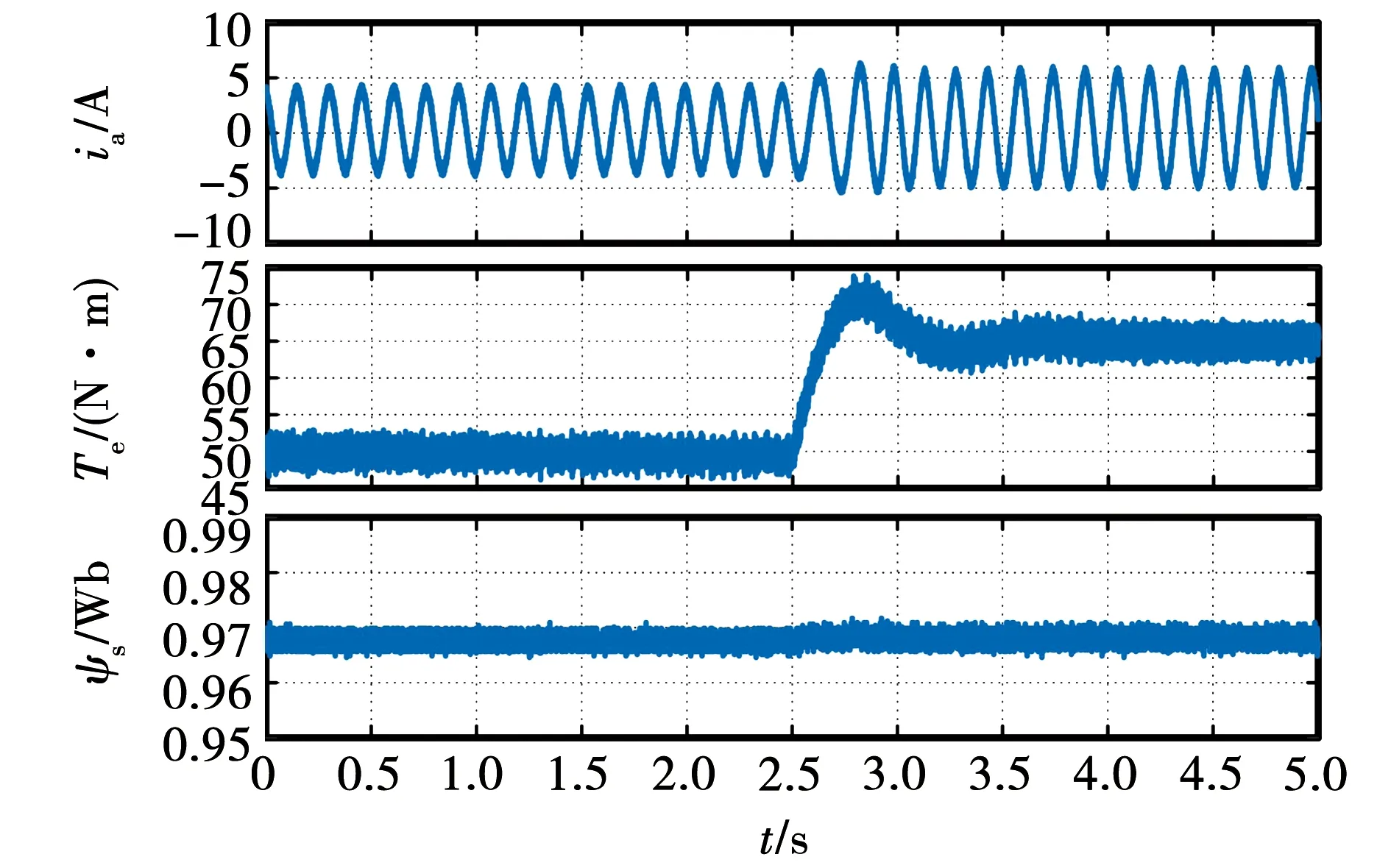
图15 本文所提控制策略动态性能Fig.15 Dynamic performance of the control strategy
4 结 论
本文所提出的基于扩展卡尔曼滤波的永磁同步电机无差拍模型预测转矩控制主要贡献如下:
1)对电磁转矩和定子磁链幅值使用无差拍控制,解出两相旋转坐标系下的参考电压矢量,将其反帕克变换至两相静止坐标系上,并送入SVPWM模块。此方法不仅省去了复杂且任务繁重的权重系数整定工作,且具有较好的稳态性能。
2)分析了定子电阻与电感对无差拍算法控制效果的重要影响。推导出定子电阻与电感出现不可抗力误差时,无差拍控制算法dq轴输出电压存在严重偏离理想值的问题。
3)针对无差拍预测转矩控制中存在参数依赖性强的问题,为提升控制策略的参数鲁棒性,本文使用扩展卡尔曼滤波器对电阻和电感进行在线辨识,并实时反馈至模型中,在参数失配的情况下,仍然可以获得良好的控制效果。
