基于DDPG算法的果蔬采摘机器人智能控制方法

范 萍

（宿迁泽达职业技术学院，江苏 宿迁 223800）

随着农业智能化发展，果蔬采摘工作目前已经实现了机械化，果蔬采摘机器人由于具有成本低、效率高、易操作等优点，目前已经被广泛应用在果蔬采摘工作中，并且得到了批量化生产。果蔬采摘机器人按照预先设定的期望轨迹进行采摘运动，但是由于果蔬采摘环境比较复杂，对果蔬采摘机器人运动具有一定的影响，在不采取任何措施的情况下，果蔬采摘机器人是无法按照设定轨迹运动的，实际运动轨迹与期望轨迹会存在较大的差距，从而导致机器人不能有效完成果蔬采摘任务。因此，对其进行智能控制是非常有必要的。但是现行方法的控制效果并不理想，在实际应用中不仅超调量比较大，而且控制稳态误差也比较大，无法满足实际需求，为此提出基于DDPG算法的果蔬采摘机器人智能控制方法。

1 建立机器人运动数学模型

为了描述出果蔬采摘机器人运动学和动力学特征，以牛顿-欧拉方程理论作为理论依据，通过建立惯性坐标系与立体坐标系，对果蔬采摘机器人的运动进行分析。以果蔬采摘机器人的重心为原点，以机器人前进方向作为X轴正方向，以机器人前进方向的右侧作为立体坐标系的Y轴，以机器人下移方向作为Z轴，建立立体坐标系。以水平面的某一点作为原点，建立果蔬采摘机器人惯性坐标系[1]。在运动空间中，果蔬机器人有6个自由度，可以通过以上建立的惯性坐标系的基本参数描述出果蔬采摘机器人的运动状态，机器人运动状态包括位置和姿态两个参数，用公式表示为：

式中，d表示果蔬采摘机器人的运动位置；X、Y、Z分别表示果蔬采摘机器人在惯性坐标系x、y、z三个坐标轴的位置；h表示果蔬采摘机器人的运动姿态；α表示机器人翻滚角；β表示机器人俯仰角；γ表示机器人偏航角[2]。

通过建立的立体坐标系基本参数描述出果蔬采摘机器人的运动速度和角速度参数，用公式表示为：

式中，v0表示果蔬采摘机器人的运动速度；e、u、c分别表示果蔬采摘机器人在立体坐标系中的纵向速度、水平速度以及垂向速度；vi表示果蔬采摘机器人的运动角速度；q表示机器人的翻滚角速度；p表示机器人的俯仰角速度；r表示机器人的偏航角速度[3]。

机器人在运动过程中，作用在机器人上的外力矩和外力表示为：

式中，σ1表示果蔬采摘机器人在运动过程中作用在机身上的外力；k、d、m分别表示纵向力、横向力和垂向力；σ2表示果蔬采摘机器人在运动过程中作用在机身上的外力矩；a表示机器人翻滚力矩；n表示机器人俯仰力矩；l表示机器人偏航力矩[4]。

考虑到果蔬采摘机器人在采摘作业当中，机器人的姿态和位置参数是实时发生变化的，因此通过对以上建立的两个坐标系进行转换，对果蔬采摘机器人的位置和姿态参数进行实时更新[5]，从而建立果蔬采摘机器人运动学数学模型，用公式表示为：

式中，τ表示果蔬采摘机器人运动学数学模型；χ表示惯性坐标系与立体坐标系转换矩阵。通过以上建立的机器人运动学数学模型，描述出果蔬采摘机器人运动状态，同时也为后续控制提供主体。

2 基于DDPG算法的机器人运动轨迹调控

在上述公式基础上，利用DDPG算法对果蔬采摘机器人运动动作进行离散化，DDPG算法属于深度强化学习算法，对机器人连续运动状态进行调控[6]，在果蔬采摘机器人运动连续动作中筛选出最优运动策略[7]，基于DDPG算法的机器人运动轨迹控制示意图如图1所示。

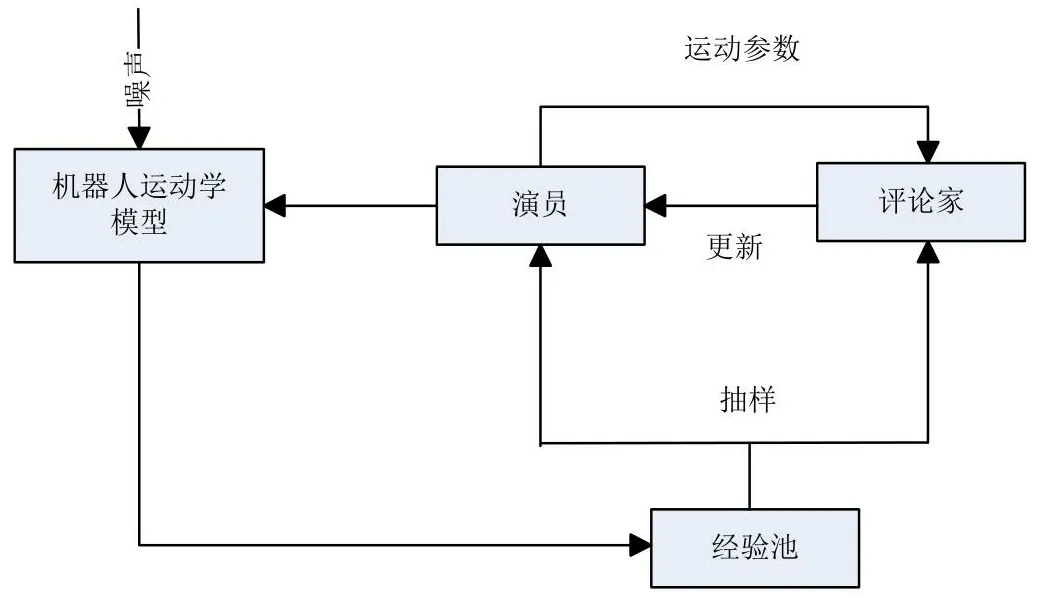
图1 基于DDPG算法的机器人运动轨迹控制示意图

如图1所示，DDPG算法是基于确定性控制策略梯度，参考深度学习网络目标和经验池重放机制，对果蔬采摘机器人运动参数进行更新，从而实现对果蔬采摘机器人运动参数自整定的[8]。基于DDPG算法的机器人运动轨迹控制，设置深度神经网络，在该网络中分为现实主网络和目标网络，主网络在深度神经网络中扮演着演员的角色，目标网络在深度神经网络中扮演着评论家的角色，将果蔬采摘机器人运动学数学模型运动参量作为DDPG算法中深度神经网络的输入向量，演员根据输入的果蔬采摘机器人运动策略给出一个新的参数，用公式表示为：

式中，f表示主网络给出的新的参数；φ表示当前果蔬采摘机器人的运动状态；ω表示深度神经网络参数；F表示奖励。

以输入的果蔬采摘机器人运动状态为基础，主网络对深度神经网络参数进行更新设置，选择出当前机器人的最优动作，向评论家（目标网络）输入下一时刻的运动状态，并且给予奖励。评论家根据经验池存放的果蔬采摘机器人运动数据选择下一个最优动作，并且对深度神经网络参数进行定期重新更新，生成果蔬采摘机器人运动目标值，用公式表示为：

式中，v表示目标网络生成的果蔬采摘机器人运动目标值；θ表示折扣因子；E表示果蔬采摘机器人当前的动作价值；Ct+1表示主网络输出的下一时刻的果蔬采摘机器人运动状态；At+1表示经验池存放的果蔬采摘机器人运动动作采样数据中下一个最优运动动作。

将生成的目标值与当前果蔬采摘机器人运动状态比对，求出果蔬采摘机器人运动轨迹误差，其计算公式为：

式中，υ表示果蔬采摘机器人运动轨迹误差；vo表示当前果蔬采摘机器人运动轨迹。将计算得到的运动轨迹误差输入控制器中，由控制器将其作为机器人参数整定值调控果蔬采摘机器人运动参数[9]，以此消除机器人运动轨迹误差，使其贴近期望运动轨迹，完成基于DDPG算法的果蔬采摘机器人智能控制。

3 实验论证

3.1 实验准备与设计

在完成基于DDPG算法的果蔬采摘机器人智能控制设计后，为检验设计方法的可靠性与可行性[10]，将以设计方法作为实验对象，选择目前两种最为常用的方法作为对照对象，设计一组对比实验。为了方便后续实验陈述，将两种传统方法用传统方法X、传统方法Y表述。选择某采摘农业园中的果蔬采摘机器人作为控制对象，该果蔬采摘机器人型号为JFATAS-4A8F4，规格为980 mm×750 mm×450 mm，整备质量为85 kg，前后轮距为650 mm，左右轴距为565 mm，越障高度为175 mm，最大载重量为150 kg，最大牵引力为1 750 N，整体材质为铸钢，最大爬坡角度为55°，最高速度为2.5 km/h，该园区共有10台果蔬采摘机器人，利用本文设计的方法对其进行智能控制。实验在32位Windows 2010系统下进行，DDPG算法使用Python 2.5编译，建立果蔬采摘机器人运动学数学模型，经过多次对DDPG算法的调试，选择较为合适的算法参数，将学习率设定为0.15，目标平滑系统设定为0.01，折扣因子设定为0.53，目标网络升级间隔设定为15，数据容量设定为128。按照上述流程对机器人进行控制，下文将对具体控制效果进行评定。

3.2 实验结果与讨论

超调量可以反映出果蔬采摘机器人的智能控制精度，超调量越大，则表示机器人控制精度越低，对于果蔬采摘机器人控制而言，超调包括角度和距离两个方面，其计算公式为：

式中，G表示果蔬采摘机器人超调量；x表示果蔬采摘机器人理想角度；x0表示果蔬采摘机器人调控后的实际角度；y表示果蔬采摘机器人理想距离；y0表示果蔬采摘机器人调控后的实际距离。

实验中随机选择8个果蔬采摘机器人，通过对果蔬采摘机器人的控制完成一次果蔬采摘动作，利用上述公式计算出果蔬采摘机器人智能控制的超调量，使用电子表格记录实验数据，具体数据如表1所示。

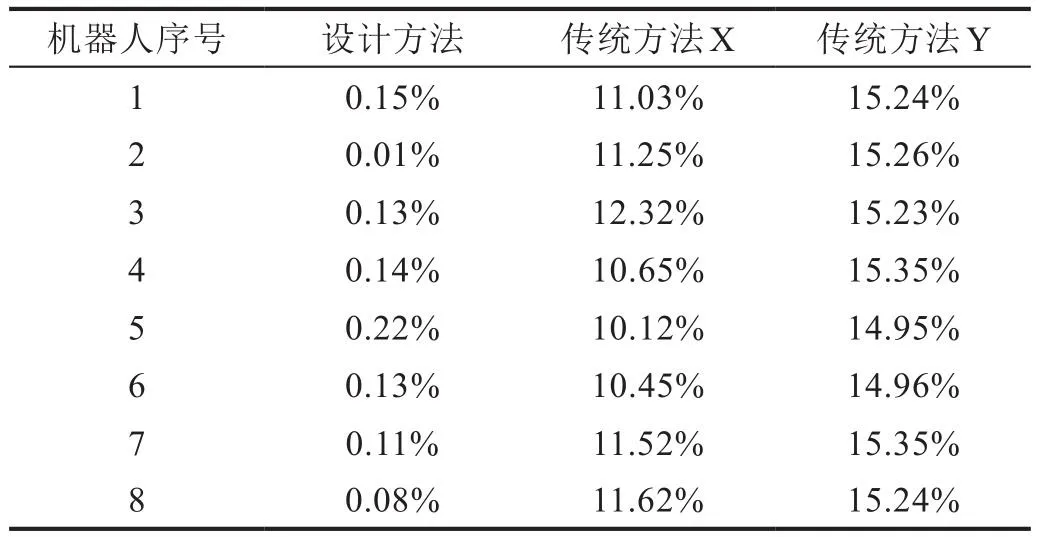
表1 三种方法超调量对比

从上表数据可以看出，三种方法在超调量方面表现出明显的差异，设计方法的最高超调量仅为0.22%，可以将超调量控制在1%以内，说明在应用设计方法时，果蔬采摘机器人运动状态与理想状态基本一致。与传统方法X相比，设计方法超调量最大约小12%；与传统方法Y相比，设计方法超调量最大约小15%。因此，从控制精度方面来看，设计方法优于两种传统方法。

单一的指标不能全面反映出方法的应用效果，因此，选择稳态误差作为第二评价指标，稳态误差越大，则表示机器人的控制精度越低。对于控制稳态误差的评价，选择角度作为参量，以控制次数作为变量，使用电子表格记录三种控制方法的稳态误差，具体数据如表2所示。

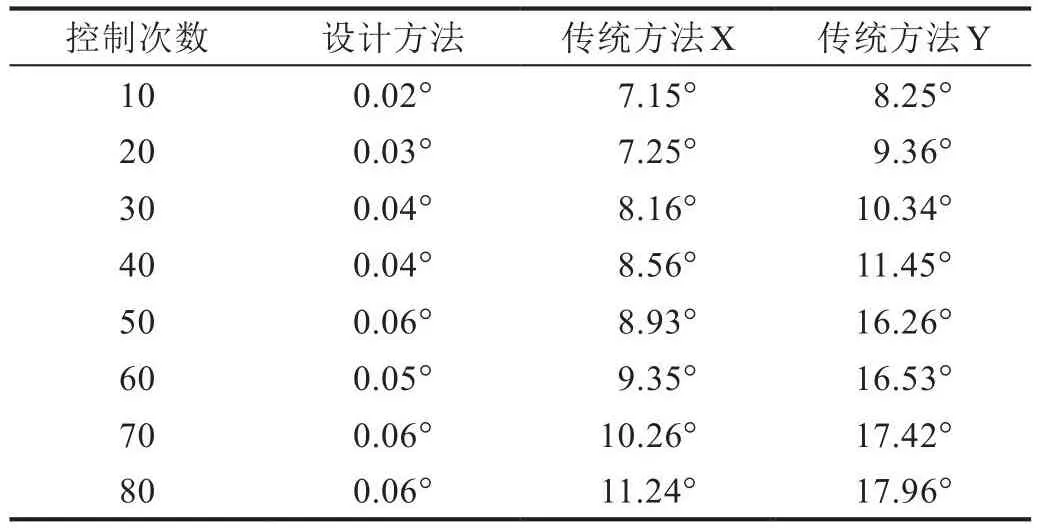
表2 三种方法稳态误差对比

从上表数据可以看出，三种方法在稳态误差方面也表现出明显的差异，设计方法的稳态误差最大仅为0.06°，数值较小，基本可以忽略不计，说明在应用设计方法时，果蔬采摘机器人不会发生偏航问题。与传统方法X相比，设计方法的稳态误差最大约小11°；与传统方法Y相比，设计方法的稳态误差最大约小18°。因此，以上实验结果可以证明，无论是在超调量方面还是在稳态误差方面，相较于两种传统方法，设计方法均表现出明显的优势，更适用于果蔬采摘机器人的智能控制。

4 结束语

为了保证果蔬采摘机器人能在复杂环境下顺利完成果蔬采摘任务，按照预先设定的期望轨迹进行准确运动，本文结合DDPG算法优势，将其应用到果蔬采摘机器人智能控制中，提出了一种新的控制方法，有效降低了果蔬采摘机器人超调量与控制的稳态误差，为果蔬采摘机器人智能控制实践提供了理论支撑，同时也为基于DDPG算法的果蔬采摘机器人智能控制方法研究提供了参考依据，有助于提高果蔬采摘机器人控制的智能化水平，具有良好的现实意义。但是该研究方法目前尚处于初步探索阶段，尚未得到大量的实践与操作验证，在某些方面或许存在不足，今后将在方法优化设计方面展开深层次探究，促进果蔬采摘机器人广泛应用与发展。