基于简单循环单元的储能锂离子电池SOC 和SOH联合估计方法*

周 航 刘晓龙 张梦迪 孙金磊 程 泽

(1.天津大学建筑设计规划研究总院有限公司 天津 300073；2.天津大学电气自动化与信息工程学院 天津 300072)

1 引言

锂离子电池是一种清洁环保的储能装置，有着体积小、寿命长、能量密度高等优势，被广泛应用于电动汽车、建筑电气、民用电子、电力系统等领域[1-2]。锂离子电池的荷电状态(State of charge，SOC)和健康状态(State of health，SOH)是电池储能系统在运维过程中所需要估算的重要参数，它们的准确估计是电池长期安全稳定运行的重要保证。

SOC 反映了电池的剩余电量，它对电动汽车的行驶里程预测、电池组的均衡控制等具有重要指导意义，主流的SOC 估计方法有安时积分法、开路电压法、自适应滤波器法、数据驱动法等。安时积分法[3]凭借着原理简单、计算量小的优势，在工业生产当中有着较为广泛的应用。但它的缺陷也比较明显，首先，它是一种开环方法，容易受到测量噪声等不确定因素的影响；其次，它要求SOC 初值必须是已知的，这使其应用范围十分受限。开路电压法[4]是一种离线方法，通过建立开路电压(Open circuit voltage，OCV)与SOC 之间的映射关系来实现对电池SOC 的估计，但OCV 的获取较为困难，需要将电池长时间静置，这使其难以在线应用。自适应滤波器法[5-6]需要结合电池的等效电路模型(Equivalent circuit model，ECM)[7]来使用。这类方法可以实现SOC 初值的自校正，并且有着一定抗干扰能力。但是这类方法十分依赖ECM 参数的准确辨识，同时自适应滤波算法中的过程噪声和测量噪声并没有明确的设置思路，通常只能根据经验法来进行获取。数据驱动法[8-9]不需要考虑电池内部的工作机制，它是在大量训练数据的基础上，通过利用机器学习模型来建立电池的SOC 估计模型。文献[10]使用门控循环单元神经网络来建立电池的SOC 估计模型，并使用动量梯度算法来对模型的训练过程进行优化，实现了电池SOC 快速可靠的估计。文献[11]使用二维卷积神经网络和双向长短期神经网络来提取电池电压、电流和温度上的信息，进而实现对电池SOC 的映射，并使用模型迁移的方法实现估计方法对电池环境温度的自适应。这类方法有着适应性强、估计精度高、简单易用等优势，但是它们的计算也较为复杂，对硬件资源和训练数据要求较高。不过近年来在大数据和硬件设备的飞速发展下，这些问题也都能得到有效解决。

SOH 反映了电池的老化情况，它是对电池进行风险预警和更换维护时所需要参考的重要参数，主流的SOH 估计方法有测量法、经验衰退模型法、数据驱动法等。测量法主要是通过阻抗[12]、容量等与电池老化直接相关的参数来对SOH 进行评估。这类方法的原理较为简单，但是缺陷也较为明显，如电池阻抗的准确测量有一定的难度，电池容量的获取需要花费大量的时间，这些原因使得这类方法的应用范围十分受限。经验衰退模型法主要是使用数学公式，如双指数函数[13]、多项式函数[14]等来对电池的老化趋势进行拟合，以此来获取电池SOH 的变化规律。这类方法有着计算量小、简单易用的优势，但是可靠性较低，容易受电池不一致性的影响，并且难以实现对复杂运行工况的适应。数据驱动法是通过提取电池外部的健康特征(Health feature，HF)[15]，并使用机器学习模型来建立HF 与SOH 之间的映射。文献[16]提取电池的放电时间、温升时间、电流曲线面积作为电池的HF，并使用经粒子群算法改良后的高斯过程回归方法来建立电池的SOH 估计模型，实现了多种环境温度下电池SOH的可靠估计。文献[17]凭借深度学习方法中卷积神经网络对非线性关系的优秀映射能力，降低了对电池HF 的选取要求，直接使用电池充电曲线上原始的电压、电流、温度采样点作为HF，同样实现了较为可靠的SOH 估计。这类方法不需要考虑电池的老化机理，使用方式也较为简单，并且有着较高的估计精度和可靠性，是当前热门的研究方向，但是也有这类方法的通病，即对训练数据的质量和硬件设备的算力有较高的要求。

现有的许多研究都是基于单参数估计来进行，然而这两参数之间存在一定的耦合联系，如在对SOC进行估计时，就必须要考虑电池最大容量的变化，即需要考虑电池SOH 的影响。可见这两个参数的估算步骤也会存在一定的重叠[18]，因此，开展SOC 与SOH联合估计的研究可以节省一定的计算步骤，具有较高的实用意义。另外，不管是SOC 估计方法中的数据驱动法，还是SOH 估计方法中的数据驱动法，都十分依赖于机器学习算法的选择。近年来深度学习方法得到了飞速发展，并衍生出许多优秀的神经网络模型，如何将这些模型本土化后应用于电池状态估计领域也是较为热门的研究方向。

为此，本文采用深度学习方法中的简单循环单元(Simple recurrent unit，SRU)来实现对电池SOC和SOH 的联合估计。首先，建立基于SRU 的电池SOC 估计模型；接着，使用含有电池老化信息的样本数据来对模型进行训练；最后，通过对该模型输出的SOC 估计值中所隐含的老化信息进行挖掘，从而完成电池SOC 与SOH 的联合估计。

2 电池SOC 与SOH

SOC 被定义为电池当前剩余电量与实际容量之间的比值，为便于实际应用，一般根据电池已释放出的电量来计算

式中，I表示电流，I在[0,t]上的积分表示电池放出的电量，Cm为电池在当前的实际容量。

随着电池使用时间的增加，其内部不可逆的老化反应会逐渐加剧，对外表现出实际容量Cm不断降低的现象。因此电池的SOH 常从容量角度进行定义

式中，C0表示电池在出厂时的额定容量。

联立式(1)、(2)可得

由式(3)可见，电池的SOC 与SOH 之间存在较为紧密的联系，SOC 的准确估计需要考虑电池当前SOH 的影响。为了更加直观地展示这一影响，在图1 中展示了电池在不同SOH 下的SOC 曲线，可以看到即使都是恒流放电工况，它们之间也有着较为明显的差异，电池SOH 越低，SOC 曲线的斜率就越大，放电过程也就越早结束。因此，为保证电池SOC估计模型在训练过程能够学习到关于电池老化的信息，本文在后续试验中制作电池SOC 标签时均按照式(3)来计算。

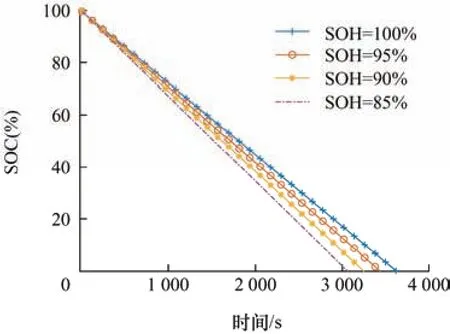
图1 不同SOH 下的电池SOC 变化曲线

3 电池SOC 估计模型

电池的SOC 估计问题是一种时间序列问题，当前时刻下的SOC 估计值与历史信息仍会存在一定的关联。因此，本节通过利用SRU 在处理时序问题上的优势，建立了基于SRU 的电池SOC 估计模型。

3.1 简单循环单元SRU

SRU[19]是一种较为新颖的循环神经网络(Recurrent neural network，RNN)，其计算过程如图2 所示，可见其在每一时刻的输入都与之前时刻的状态信息存在着紧密联系。为解决传统RNN 在处理长序列时出现长期依赖的问题，SRU 的内部设有门控结构来调整信息的流向。相较于流行的RNN变体，如长短时神经网络(Long short-term memory networks，LSTM)和门控循环单元(Gate recurrent unit，GRU)，SRU 在进行训练的过程中能将大部分计算并行处理，仅保留了必要的串行计算，因此它具有更快的训练速度。同时，SRU 与LSTM和GRU 的性能相近，甚至能够通过叠加隐藏层的层数来获得更为优秀的性能。SRU 的内部结构如图3 所示。

图2 SRU 计算过程图

图3 SRU 内部结构图

计算方法为

式中，xt为输入量；ft和rt为遗忘门和重置门；c和h为状态量和输出量；W和b为权重和偏差；σ为sigmoid 函数。可以看到SRU 中遗忘门和重置门的计算仅与当前时刻下的输入信息有关，与前一时刻的状态信息并不存在联系，这也是SRU 能够实现并行训练的保证。

3.2 基于SRU 的SOC 估计模型

在电池的放电过程中，电池端电压会发生相应的变化，不同SOC 所对应的电压值会存在一定的差异，可见这一特性可以用来实现对电池SOC 的估计。然而，电池的放电过程会受到老化的影响，在不同SOH 下，电池端电压和SOC 之间的映射关系也会有所不同。SOC 估计模型要想能够实现对电池老化的自适应，就必须在训练过程中使用含有电池老化信息的数据来训练，即使用考虑电池SOH 后的SOC 值作为模型训练集的标签。但是单个时刻下的电压信息量较少，难以克服电池老化的影响来实现与SOC 之间的可靠映射。因此，本节在建立电池SOC 估计模型时引入了数据单元[20]的输入形式。参考文献[20]，将数据单元设置为由连续10 个时刻下电压采样点组成的数据片段。数据单元是SOC 估计模型能够实现在任意SOH 下进行准确SOC 估计的重要基础。

基于SRU 的SOC 估计模型主要由SRU 和全连接网络(Fully connected network，FCN)两部分组成。其中，SRU 负责接收输入信息以及传递历史信息，它是SOC 估计模型的核心部分，它的输入尺寸设置为10×1，层数设置为2，每层节点个数设置为300；FCN 负责对SRU 的输出进行降维后输出相应的SOC 估计值，它由输入层、隐藏层和输出层组成，它的输入层输入尺寸大小与SRU 输出保持一致，即300×1，它的隐藏层设置为两层，对应的节点个数分别设置为150 和50。为了提高FCN 对非线性关系的表达能力，在每个隐藏层后面添加ReLu 激活函数层。模型的其他设计内容如下所示。

(1) 数据预处理：在对模型训练前，使用归一化的方法对样本数据进行预处理。归一化与反归一化计算方法分别为

式中，x表示原始值，xmax表示原始值中的最大值，xmin表示原始值中的最小值。

(2) 损失函数：在对模型训练过程中，使用均方差函数(Mean square error，MSE)作为损失函数。

(3) 优化器：使用Adam 作为模型训练的优化器，初始学习率设置为0.001，模型训练的迭代次数设置为1 000。

该模型的工作流程如图4 所示，可以看到该模型每次的输入为由10 个时刻下的电池端电压值组成的数据单元，每获取一个数据单元就进行一次SOC 估计。

图4 SOC 估计模型工作流程图

4 SOC 与SOH 联合估计方法

由第3.2 节可知，所提SOC 估计模型在训练过程中使用了含有电池老化信息的数据来进行训练。后续试验会证明所提SOC 估计模型在对样本数据进行有效学习之后，可以实现任意电池老化程度下的SOC 估计。本节利用该模型的这一能力，通过对SOC 估计值中所隐含的老化信息进行挖掘，从而实现SOC 与SOH 的联合估计，其运算过程如图5 所示，具体推导如下所示。

图5 SOC 与SOH 的联合估计

由式(3)可知，在电池放电过程中，t=t1和t=t2时的SOC 表达式分别如式(7)和式(8)所示，其中t1小于t2。

将式(7)和式(8)做差计算后，易推导得到

可见获取SOH 估计值的关键就是模型在t1和t2时刻下对电池SOC 的准确估计。考虑到模型在估计SOC 时会存在一定的误差，若这两个估计时刻的间隔较短的话，SOC 变化量较小，模型估计误差就会占较大的比例，影响SOH 估计的准确性。此外，考虑到模型在初始估计时刻可能会出现一定的波动，因此，本节将t1时刻选择为模型在第10 个数据单元所对应的时刻，t2选择为放电结束的时刻。当获得这两个时刻下的SOC 估计值与放电过程所释放的电量，即可通过式(9)完成对SOH 的估计。

5 试验结果与分析

本节在Pytorch 深度学习库的基础上完成电池状态估计模型的搭建。为了验证本文所提SOC 和SOH 估计方法的有效性，本节分别使用由牛津大学[21]和美国航空航天局(National Aeronautics and Space Administration，NASA)公开发表的锂电池数据集[22]中的测试数据来进行试验，并使用均方根误差(Root mean squared error，RMSE)、绝对误差(Absolute error，AE)、平均绝对误差(Mean absolute error，MAE)和最大绝对误差(Maximum absolute error，MAX)来对SOC 和SOH 的估计结果进行定量评估

式中，x和ˆx分别表示它们的真实值和估计值。

5.1 试验所用数据集的介绍

牛津大学电池数据集的测试对象为8 块额定容量740 mA·h，额定电压4.2 V 的钴酸锂离子电池，它们的编号记为Cell1，Cell2，…，Cell8。这些电池在环境温度40 ℃下进行了循环放电测试，具体测试步骤如下所示。

(1) 使用1.48 A 的恒流对电池进行充电。

(2) 使用模拟电动汽车动态工况对电池进行放电。

(3) 重复前两个步骤，并每隔100 次循环，使用0.74 A 的恒流对电池进行放电，截止电压设置为2.7 V，以此来对电池实际容量Cm进行标定。

图6 展示了测试电池的SOH 变化曲线，可以看到随着循环次数的增加，这些电池的SOH 都会有所下降。图1 展示了电池Cell1 在不同SOH 下的SOC曲线。一般来说，当电池SOH 下降至80%时即可认为其寿命终止[23]，本文为了验证所提估计方法的可靠性，使用电池在全生命周期下的测试数据来进行试验。

图6 牛津大学电池数据集的SOH 变化曲线

NASA 电池数据集的测试对象为3 块额定容量2 A·h，额定电压4.2 V 的18650 锂离子电池，它们的编号记为B0005、B0006、B0007。这些电池在室温25 ℃下进行了循环放电测试，其测试步骤如下所示。

(1) 使用恒流(1.5 A)-恒压(4.2 V)的方式来对电池充电。

(2) 使用2 A 的恒流对电池进行放电，截止电压分别设置为2.7 V、2.5 V 和2.2 V。

(3) 重复前两个步骤。

考虑到这三块电池的放电截止电压有所不同，为了保证在计算电池实际容量Cm时标准的统一，规定2.7 V 为三块电池统一的放电截止电压。图7 展示了其SOH 的变化曲线。

图7 NASA 电池数据集的SOH 变化曲线

在对电池状态估计模型进行训练和测试时，必须要保证训练集与测试集的相互独立。在两个电池数据集中训练集与测试集的划分情况如表1 所示。在对模型进行训练时，需要使用电池在全生命周期下的放电数据进行训练。同样地，在对训练好的模型进行性能测试时，也要使用电池在全生命周期下的放电数据。

表1 训练集与测试集的划分情况

5.2 SOC 估计结果

按照表1 分别在两个电池数据集上对SOC 估计模型进行训练与测试。训练好的模型在两个数据集上的SOC 估计结果如图8 所示，图8 中包括了电池在特定SOH 下的SOC 估计结果(电池Cell7 在SOH为95%时的SOC 估计曲线及AE 曲线、电池Cell8在SOH 为85%时的SOC 估计曲线及AE 曲线、电池B0007 在SOH 为90%时的SOC 估计曲线及AE曲线)，以及SOC 估计模型在3 块电池上估计误差RMSE 和MAE 随循环次数增加而变化的曲线，其中RMSE 和MAE 由每一次循环下的SOC 估计结果计算所得。

图8 SOC 估计结果

图8a～8b 为模型在牛津电池数据集上的估计结果，可以看到电池在特定SOH 下SOC 估计的绝对误差基本在2%以内，估计值可以很好地跟随真实值，表现出了较高的估计精度。同时可以看到，虽然电池在SOH 为95%和85%时均为恒流放电工况，但是它们的放电曲线在电池老化的影响下也有着较为明显的差异。而所提SOC 估计模型能够很好地适应这种差异，训练好的模型可以直接用来在不同SOH下进行SOC 估计。此外，通过观察误差变化曲线可以看到，在电池全生命周期下的估计误差RMSE 和MAE 都可以维持在较低的水平，这表明该模型基本实现了对电池老化程度的自适应，可以在任意SOH下完成对电池SOC 的可靠估计。

图8c 为模型在NASA 电池数据集上的SOC 估计结果，可以看到该结果与在牛津数据集上的类似，不仅在特定的SOH 下能够实现较高精度的SOC 估计，而且在电池全生命周期下的估计误差RMSE 和MAE 也基本保持在了较低的水平，同样能够实现对电池老化程度的良好适应。这一结果也表明，本文所提的SOC 估计方法可以适用于不同种类的锂离子电池，有着较好的泛化能力。

表2 给出了使用各个电池上全部估计点计算得到的RMSE 和MAE 以及估计过程中出现的MAX。可以看到RMSE 和MAE 均在1%以内，MAX 也不超过5%，这再次表明该模型有着较高的估计性能，在电池的整个生命周期下都能够实现准确可靠的SOC 估计。

表2 SOC 估计结果

5.3 SOH 估计结果

在第5.2 节中已经证明了所提SOC 估计模型能够在任意电池老化程度下进行可靠的SOC 估计，这也是本文所提SOC和SOH联合估计方法实现的重要基础。

图9 展示了将训练好的SOC 估计模型应用于联合估计方法后，在三块电池上的SOH 估计曲线及AE 曲线。其中，图9a～9b 是所提联合估计方法在牛津电池数据集上的估计结果，可以观察到电池Cell7 和Cell8 的SOH 衰退速率有着较为明显的差异，SOH 下降至80%所经历的循环次数有着明显的不同，这种电池之间的不一致性也对SOH 估计方法的可靠性有了更高的要求。但是该联合估计方法可以克服这种电池不一致性带来的影响，它在两块电池上SOH 估计值均能有效地收敛于真实值，SOH 估计的绝对误差基本在1.5%以内，表现出了较高的估计精度。图9c 展示了联合估计方法在NASA 电池数据集上的估计结果，可以看到电池B0007 的SOH 衰退曲线上存在较为明显的容量增生现象，曲线的波动起伏较为剧烈，这势必会给SOH 估计方法带来不小的挑战。但是所提方法基本不受这一现象的影响，SOH估计值仍然有较高的估计精度，估计绝对误差基本限制在2%以内。这一结果也表明，所提联合估计方法对不同种类的电池也有良好的通用能力。

图9 SOH 估计结果

表3 给出了所提联合估计方法在三块电池上SOH 的定量估计结果，可以看到在这些电池上的估计误差RMSE 和MAE 均小于1%，并且最大绝对误差MAX 不超过3%，这些误差评价指标均保持在了较低的水平，这一结果充分说明了本文所提联合估计方法的有效性。

表3 SOH 估计结果

6 结论

本文通过对锂离子电池SOC 与SOH 之间的联系进行分析，并基于SRU 方法形成了一种电池SOC和SOH 的联合估计方法。

(1) 该方法利用SRU 在处理序列问题上的优势，建立了基于SRU 结构的SOC 估计模型。为了使训练好的SOC 估计模型能够实现对电池老化的自适应，给模型引入了数据单元的输入形式，并使用考虑SOH 后的SOC 值来作为训练集的标签。试验结果表明，该模型可以在任意电池老化程度下实现SOC 的准确估计，并且可以适用于不同种类的电池，有着较好的泛化能力。

(2) 该方法通过对模型输出的SOC 估计值中所隐含的老化信息进行挖掘，形成了一种电池SOC 与SOH 联合估计方法。试验结果表明该方法可以有效利用SOC 估计值中的老化信息，能够获得较为可靠的电池SOH 估计值。

综合来看，本文所提方法的估计步骤较少，应用方式较为简单，具有较强的实用意义。