前置滤波器永磁同步电机的电流环参数多目标优化设计
2023-11-02许家群陈腾宇
许家群 陈腾宇
(北京工业大学信息学部 北京 100124)
1 引言
永磁同步电机(Permanent magnet synchronous motor,PMSM)与逆变器间加入LC 滤波器是降低高频电流谐波的有效手段[1]。考虑到体积和电磁干扰因素,滤波器更适宜独立于逆变器布置,电机控制系统相电流检测传感器由此便于布置在逆变器侧[2-3]。不同于传统电机系统,引入LC 滤波器后,电流环控制器比例积分(Proportional integral,PI)参数不仅决定电机动态与稳态性能,还对系统稳定性和谐振性能及高频谐波产生影响[4-8]。因此,研究电流环PI 参数设计方法,对于改善前置滤波器电机系统性能极具实用价值。
传统电机系统PI 参数设计方法的研究较多。其中,Ziegler-Nichols 法[9]和零极点相消法[10]得到广泛应用。Ziegler-Nichols 法不需要识别系统参数,通过寻找稳定极限确定PI 增益,但未考虑其余性能指标。零极点相消法忽略影响中低频段较小的环节,结合截止频率调整PI 参数,使电机传递函数极点与控制器零点相抵消,以提高系统动态性能。近年来,对传统参数整定方法也进行了不少改进。文献[11]基于零极点相消法和PMSM 系统频域模型,考虑了逆变器死区和延时等因素,推导出电流环PI 控制器参数与开环截止频率和相位裕度关系,受界定范围影响,其PI 参数取值范围较大且需要多次比对。在文献[11]的基础上,文献[12]通过建立最小评价函数迭代学习最优开环截止频率,简化了计算步骤,提高了系统响应速度,但超调量等性能未能兼顾。文献[13]分析了电流环带宽、延迟与PI 参数关系,进而通过改变PI 参数以提高电流环动态响应能力。文献[14]通过预测控制与PI 控制结合,提高了系统动态性能并拓展了PI 参数稳定域。文献[15]建立了PMSM 控制系统离散模型,将时域性能指标转换成频域特征量,通过频域分析进行PI 参数整定。文献[16]提出一种多目标设计方法,通过分析PI 参数与时域指标、频域指标和系统参数的关系,确定可直接取值的PI 参数期望区域,但PI 参数取值范围较广。
关于前置滤波器电机系统的电流环参数设计研究较少。传统的Ziegler-Nichols 法与系统结构无关,零极点相消法着重关注中低频段,因而这两种方法可用于前置滤波器系统,但性能有限。在文献[11-16]中,PI 参数设计方法均面向无滤波器传统电机系统,均未涉及引入滤波器后的谐振和稳定性问题。可见,针对前置滤波器电机系统,其电流环参数设计问题尚未有效解决,还需要全面考虑PI 参数对系统性能的影响,进而在满足稳定性基础上最大化兼顾系统综合性能需求。
本文针对前置LC 滤波器PMSM 系统,研究其电流环PI 参数设计方法,推导逆变器侧电流反馈系统开环传递函数,分析PI 参数对系统稳定性、动态性能、带宽以及谐振峰值的影响,在此基础上确定PI 参数稳定域并给出优化目标及其约束范围,通过遗传算法求解电流环参数,并进行系统仿真验证。
2 逆变器侧电流反馈系统数学模型
图1 为前置LC 滤波器的PMSM 系统矢量控制结构框图,其中的相电流iinva、iinvb和iinvc检测位于逆变器侧。在d-q旋转坐标系下,前置LC 滤波器PMSM 系统的电压和电流方程如式(1)~(6)所示。
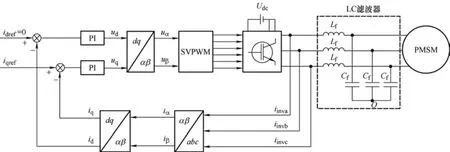
图1 前置滤波器PMSM 系统矢量控制结构框图
式中,iinvd、iinvq分别为逆变器侧d、q轴电流;isd、isq分别为电机侧d、q轴电流;uinvd、uinvq分别为逆变器侧d、q轴电压;usd、usq分别为电机侧d、q轴电压;ωe为电角速度;Ld、Lq分别为d、q轴电感;Rs为定子电阻;ψf为永磁体磁链。由式(1)~(6)可得前置滤波器PMSM 系统的q轴电流环框图如图2 所示。其中,PI 控制器GPI(s)如式(7)所示,逆变器Ginv(s)如式(8)所示,Kp、Ki分别为比例系数和积分系数,Td为采样与传输延迟。

图2 逆变器侧电流反馈系统电流环
根据图2,由梅森公式计算可得电流环q轴开环传递函数Gq(s),如式(9)所示
本文研究的电机系统参数如表1 所示。

表1 电机与滤波器参数
3 电流环PI 参数对系统性能的影响
3.1 电流环PI 参数对系统稳定性的影响
由式(9)结合表1 参数可得,前置滤波器系统的电流环开环传递函数Gq(s)如式(10)所示。其根轨迹增益K=3.124 7Ki,零点分别为z1,2=-88.9±2 633.7i,z3=-Ki/Kp,极点为p1,2=-12.7±6 971.9i,p3=-6 666.6,p4=-152.4,p5=0。
前置滤波器系统闭环传递函数如式(11)所示
由闭环特征方程D(s)=0 可知,Kp、Ki直接影响根轨迹走向,不当配置会出现右半平面极点,造成系统不稳定。由于系统特征根之和为常数,此时零点和与极点和相等,如式(12)所示
由式(12)计算得到,当Ki/Kp=6 666.6 时,z3与p3重合;当Ki/Kp>6 666.6 时,z"3位于p3左侧;当Ki/Kp<6 666.6 时,z'3位于极点p3右侧。将对应三种PI 参数代入式(10),可得根轨迹曲线如图3 所示。其中Lp1、Lp2,L'p1、L'p2,L"p1、L"p2分别受z3、z'3、z"3影响并以p1、p2为起点。由图3 可知,当Ki/Kp>6 666.6 时,系统不稳定;当Ki/Kp=6 666.6 时,系统临界稳定;当Ki/Kp<6 666.6 时,系统稳定,此时根轨迹曲线位于左半平面,为最小相位系统。

图3 PI 参数对根轨迹的影响
式(10)所示开环传递函数分母高于分子2 个阶次,幅值裕度始终满足稳定要求[17],保证系统稳定只需要满足约束式(13)所示相位裕度即可。
期望相位裕度Pm≥40°[11],结合最小相位系统稳定约束Ki/Kp<6 666.6,绘制PI 参数取值范围如图4 所示。在图4 所示最小相位系统内,取Pm≥40°箭头所示区域作为本文所提方法的PI 参数稳定域。

图4 满足稳定条件的PI 参数取值范围
3.2 电流环PI 参数对谐振峰值的影响
前置滤波器会使系统在谐振频率ωres处产生较大谐振峰值,ωres可表示如下[18]
由式(14)可得到本文系统ωres=6 972 rad/s,对应1 109 Hz。根据式(10)所示系统开环幅频特性,谐振峰值Mr可通过式(15)计算得出。
谐振峰会影响电流谐波幅值和谐波畸变率[3-7],应在保证系统稳定基础上削减谐振峰值。由式(15)绘制Mr与PI 参数关系如图5 所示,可见,Mr与Kp和Ki有关,且Kp影响更明显,Kp应取小以降低Mr。

图5 PI 参数对谐振峰值的影响
3.3 电流环PI 参数对系统动态性能的影响
动态性能由超调量σ%、上升时间tr和调节时间ts描述[19-20],可由式(16)所示时域特性表达式得到,其中1/s为单位阶跃输入传递函数,c(t)为系统输出,L-1为拉普拉斯反变换算子。
在图4 所示Pm≥40°区域内,选取三组Ki相同、Kp不同和Kp相同、Ki不同的PI 参数,由式(16)绘制单位阶跃响应曲线如图6 所示。可见,当Ki不变时,σ%、ts和tr均随Kp增大而减小;当Kp不变而Ki增大时,σ%随之增大,ts和tr随之减小。绘制PI 参数与动态性能指标的三维关系如图7 所示,结合图6 可见,Kp越小或Ki越大时,σ%越大,ts和tr越小。

图6 PI 参数对动态特性的影响
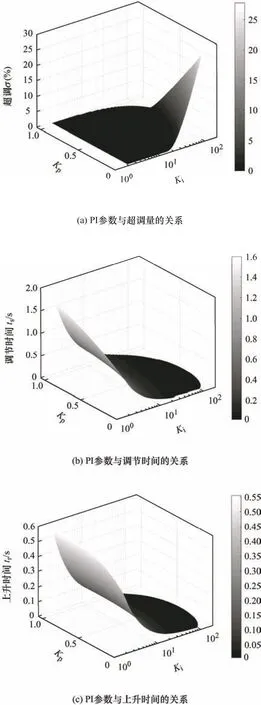
图7 PI 参数与系统动态特性的关系
3.4 电流环PI 参数对系统带宽的影响
电流环带宽取闭环幅频特性-3 dB 或相频特性-90°对应频率中的较小值[13],即
本文电机额定转速为500 r/min,对应角频率为209.4 rad/s,带宽bω取值应满足如下条件
应用与图6 相同的PI 参数,绘制闭环系统伯德曲线如图8 所示。图8a 为Ki不变时Kp对电流环带宽的影响。可见,带宽随Kp增大而变大,结合图6a 可知,带宽大的系统响应速度快,上升时间和调节时间小,超调量小。

图8 PI 与系统闭环带宽的关系
图8b 为Kp不变时Ki对带宽的影响,可见,带宽随Ki的增大而增大,结合图6b 可知,带宽越大,系统响应速度越快,上升时间和调节时间越小,超调量大。因此,可通过调节PI 参数,使系统具有较大的带宽,进而提高系统响应速度,获得较小上升时间tr和调节时间ts。
4 电流环PI 参数多目标优化
由以上分析可知,前置滤波器电机系统的带宽与动态性相关,高带宽系统响应速度快、调节时间ts和上升时间tr短,从动态性能角度可选取带宽bω作为优化目标,以扩展电流环带宽提高系统的动态响应[21]。超调量σ%单独作为优化目标之一。同时,为了降低谐振峰值减小高频电流谐波,将谐振峰值也作为一个优化目标。
针对闭环带宽、超调量和谐振峰值目标,本文采用遗传算法(Genetic algorithm, GA)优化设计电流环PI 参数,设计过程如下所示。
步骤1:PI 参数取值范围确定。根据前述分析,系统各性能指标受PI 参数的影响不同,为获得良好的综合性能,要求相位裕度Pm≥40°,带宽bω>209.4 rad/s,调节时间ts<0.02 s,超调量σ%<2%,谐振峰值尽可能小。
绘制满足上述性能要求的PI 参数范围如图9 所示。其中,四个标记点所围成的四边形区域即为满足上述性能要求的约束区域,也是PI 参数多目标寻优的取值范围。

图9 PI 参数多目标约束范围
步骤2:多目标优化模型构建。以闭环带宽bω最大、超调量σ%和谐振峰值Mr最小作为优化目标,以图9 所示约束区域作为种群取值范围,以Kp和Ki作为设计变量,构建多目标优化模型如式(19)所示
式中,f1(x)、f2(x)、f3(x)分别为bω、σ%和Mr的函数,描述三个优化目标与PI 参数的关系;R(x)表示满足x条件的PI 参数取值范围。
当在稳定域内随机取值PI 参数时,对应的f1(x)、f2(x)、f3(x)的值可分别通过式(17)、式(16)、式(15)计算得到。
步骤3:遗传算法寻优。在图9 所示PI 参数多目标约束范围中,配置种群规模为30,应用式(19)对种群中个体进行评价,将性能好的个体保存到下一代,两次迭代之间数据交叉概率取为0.8,变异概率取为0.2,迭代500 次。遗传算法寻优得到的PI参数解集如图10 所示,其对应的优化目标数值构成图11 所示Pareto 前沿。根据图10 和图11,考虑超调量小、谐振峰小和闭环带宽大的需求,本文选取Kp=0.556,Ki=107.04 作为PI 控制器参数,该取值可使系统有较小超调(σ%=0.83)和较小谐振峰值(Mr=32.7 dB)及较大带宽(bω=358 rad/s),从而保证系统良好的综合性能。

图10 PI 参数解集
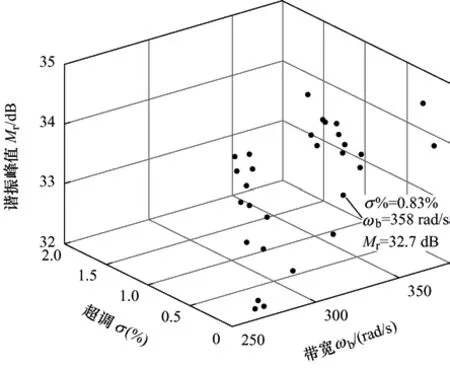
图11 Pareto 前沿
5 与传统参数设计方法的性能比较
应用传统Ziegler-Nichols 法设计本系统参数,如图12 所示,当调节临界比例度Kc=1.5 时,系统临界振荡周期Tc=0.001 s。由经验公式Kp=0.45Kc、Ki=Kp/0.833Tc可得Kp=0.675,Ki=810.3。

图12 临界振荡曲线
应用传统零极点相消法设计本文系统参数时,将表1 数据代入式(9),忽略较小影响中低频段环节,传递函数极点与控制器零点抵消,将电流内环校正为一阶系统。由此,PI 参数设计为Kp/Ki=6.56×10-3,电流环开环传递函数化简为Gqx(s)=3.124 7Ki/s,结合式(17)可求得带宽与PI 参数关系为Ki=ωb/3.124 7。再由式(19)可绘制Pm≥40°稳定域内PI 参数与带宽关系如图13 所示,可以看出能实现的最大带宽约为300 rad/s,进而可计算出Kp=0.63,Ki=96。

图13 PI 参数与带宽的关系
三种设计方法PI 参数下系统开环和闭环频域波形以及闭环时域波形分别如图14a~14c 所示。其中,相位裕度和谐振峰值可由图14a 获得,带宽可由图14b 得到,动态性能可由图14c 得到。以上性能指标如表2 所示。
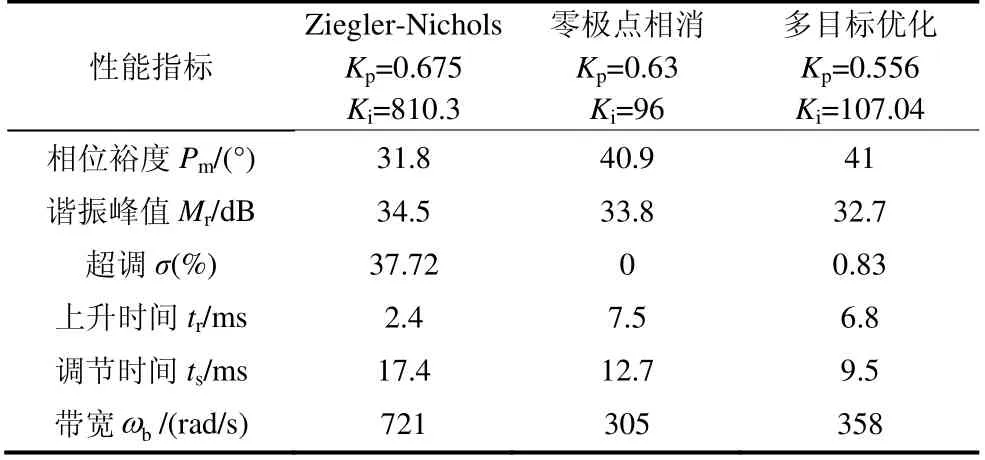
表2 不同整定方法控制器性能

图14 不同PI 参数设计方法系统性能对比
由图14 和表2 可见,三种方法系统稳态误差均趋于 0 。 Ziegler-Nichols 法相位裕度较小(Pm=31.8°),谐振峰值大(Mr=34.5 dB),带宽大(bω=721 rad/s),响应速度快(tr=2.4 ms),但超调过大(σ%=37.72%),稳态调节时间长(ts=17.4 ms)。零极点相消法系统稳定性提高(Pm=40.9°),谐振峰值降低(Mr=33.8 dB),超调约为 0,但带宽小(bω=305 rad/s),响应速度较慢(tr=7.5 ms),稳态调节时间较长(ts=12.7 ms)。本文所提多目标优化方法通过对超调、带宽和谐振峰值进行综合寻优,系统稳定性好(Pm=41°),谐振峰值低(Mr=32.7 dB),带宽较大(bω=358 rad/s),并具有较好的动态性能(σ%=0.83%,tr=6.8 ms,ts=9.5 ms)。
6 仿真验证
针对传统Ziegler-Nichols 法、零极点相消法和本文多目标优化方法分别设计的PI 参数,进行系统仿真。比较三组不同PI 参数系统的如下性能:电流阶跃系统动态和稳态性能;正弦电流频率逐渐增加的电流环带宽;额定工况电流跟踪响应;谐振峰值和谐波抑制能力。
验证三种设计方法系统稳态和动态性能如下。图15 给出了q轴给定13 A 电流阶跃响应仿真波形。由图15 可见,不同参数系统均具有良好稳态性能。Ziegler-Nichols 法的系统响应速度快,上升时间为2 ms,但超调量过大,约为33.33%,且调节时间长达16 ms。零极点相消法的超调量基本为0,但动态性能差,响应速度慢,tr=7 ms,ts=13 ms。多目标优化方法基本零超调,相较于零极点相消法响应速度也大大提升,tr=6 ms,ts=7 ms。上述指标与表2 相符。
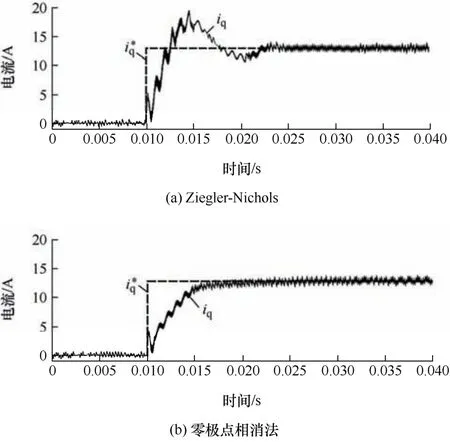

图15 阶跃响应电流仿真波形
为验证三种设计系统电流环带宽,进行如下测试[22]。给定幅值13 A、频率从1 rad/s 逐渐增大的正弦信号,直至反馈信号幅值降至0.707 倍或相位滞后90°。测试得到Ziegler-Nichols 法、零极点相消法和多目标优化法对应的系统带宽分别为611 rad/s、280 rad/s 和325 rad/s,如图16 所示。
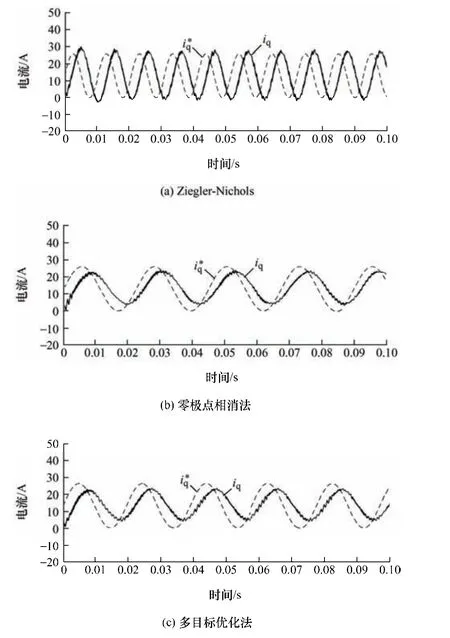
图16 不同方法带宽测试
验证三种方法系统电流环跟踪性能如下。q轴正弦给定幅值 13 A、频率 33.33 Hz (对应500 r/min),电流响应如图17 所示。可见,Ziegler-Nichols 法可准确追踪给定信号,幅值几乎无衰减,跟踪延迟小(约为0.49 ms),对应相位滞后5.91°。零极点相消法的系统带宽最小,跟踪电流幅值衰减约2 A,约占给定幅值的15.3%,跟踪延迟约为2.99 ms,对应相位滞后35.99°。多目标优化方法中电流幅值衰减约1.49 A,占给定幅值的11.5%,跟踪延迟约为2.49 ms,对应相位滞后29.99°,优于零极点相消法的跟踪性能。
三种设计方法的系统谐振性能可通过谐振频率处(ωres=6 972 rad/s,对应1 109 Hz)的电流谐波进行比较分析。额定工况的逆变器侧q轴电流频谱如图18 所示。由图18 可见,Ziegler-Nichols 法系统谐振峰值最大,ωres处电流谐波幅值占比Hres=4.39%,谐波畸变率THD=10.38%。零极点相消法系统谐振峰值及谐波含量均有下降,Hres=3.81%,THD=10.18%。与两种传统方法相比,多目标方法系统谐振峰值和谐波含量更低,Hres=3.52%,THD=10.01%。
综合上述仿真结果得到系统性能如表3 所示。三种设计方法系统仿真性能与表2 理论计算性能相符。其中,Ziegler-Nichols 法系统带宽较大,但超调和高频谐波也最为严重。零极点相消法系统带宽小,电流响应速度较慢。多目标优化法系统可以权衡优化多项性能指标,在保证系统良好动态性能的同时,又能够有效抑制谐振峰和电流高频谐波。
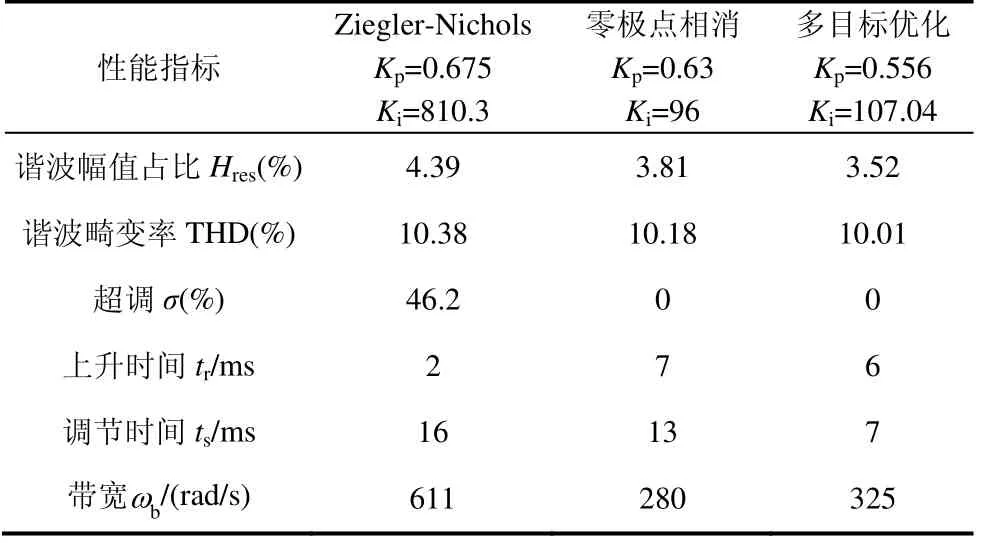
表3 不同整定方法系统性能仿真比较
7 结论
针对逆变器侧电流反馈的前置滤波器永磁同步电机系统,本文提出一种电流环PI 参数多目标优化设计方法,进行了理论分析和仿真验证,并与两种传统参数设计方法进行了比较,得出如下结论。
(1) 多目标优化方法可兼顾超调量、带宽、谐振、谐波、上升和调节时间等系统多个性能指标,传统Ziegler-Nichols法及零极点相消法则难以做到。
(2) 与传统Ziegler-Nichols 法相比,多目标优化方法系统通过适当减小带宽及电流跟踪能力,可以大大降低超调量、谐振峰值及逆变器侧电流谐波。
(3) 与传统零极点相消法相比,多目标优化方法系统超调同样较小,电流环带宽更大,电流跟踪能力更好,谐振峰值及高频电流谐波有效降低。
