基于蠕变试验下高边坡稳定性模拟研究

杨志斌

(1.中煤科工西安研究院(集团)有限公司,陕西 西安 710077;2.陕西省煤矿水害防治技术重点实验室,陕西 西安 710077)

0 引 言

支党河特大桥是湫坡头(陕甘界)至旬邑高速公路关键控制性工程之一,桥梁最高主墩可达175 m,是国内同期在建的最高刚构桥,位于黄土沟壑地区,跨越滑坡体,从安全角度来看,在建设桥墩时要对坡体进行开挖治理[1-3],但随着时间推移,仍不排除存在滑坡的可能性。因此,有必要从研究天然黄土的蠕变试验出发,分析不同时期内坡体的安全稳定性,从而推演桥梁全寿命周期内,边坡滑移破坏规律。

蠕变效应引起的滑坡灾害在短时间内难以察觉且危害较大[4-9],众多学者在研究蠕变效应过程中取得了大量成果,如陈琼等采用不同的加载方式,开展滑带土在不同固结状态下的剪切蠕变试验[10];罗汀等考虑到黄土具有蠕变特性,通过试验研究了加载路径对黄土一维蠕变特性的影响[11];LIU等通过阶跃载荷试验分析黄土蠕变行为,得到了Q2黄土的位移-时间关系[12];李昂等开展了原状黄土在不同应力状态下的蠕变特性试验研究[13];龙建辉等对黄土滑坡区试样进行不同应力状态下的直剪蠕变试验,研究其蠕变变形特性[14];WANG对某地区滑坡滑动带试样进行剪切蠕变试验,分析滑动区的蠕变特性[15];刘清秉等针对黄土边坡原状滑带土开展环剪试验,对不同应力状态下滑带土蠕变变形规律进行研究[16];褚峰等利用一维蠕变仪研究黄土在不同竖向荷载作用下的蠕变特性[17]。

另外,国内学者对蠕变模型进行了大量的理论和试验研究,杨超等认为硬岩在不同的应力区间下其蠕变特性存在较大差异,并建立了硬岩全阶段损伤蠕变模型[18];王智超等对炭质板岩进行压缩蠕变试验,通过试验结果建立了岩石蠕变本构模型[19];周瑞鹤等分析粉砂岩在不同围压下的蠕变特性,建立了粉砂岩卸载蠕变模型[20];魏尧等研究饱和冻结砂岩的蠕变特性,提出了考虑温度及损伤效应的本构模型[21];LIN等在经典的Burgers模型中引入非线性黏塑性元件,并通过岩体结构面的剪切蠕变试验来验证其合理性[22];CAO等基于岩石蠕变特性和损伤变量,结合改进的Burgers模型,得到了高应力状态下软岩的非线性损伤蠕变本构模型[23]。

上述学者多数针对单纯蠕变规律开展试验研究,对原状黄土得到的蠕变模型进行模拟反演分析较少涉及。因此,文中以实际工程为研究背景,对天然黄土开展剪切蠕变试验,给出蠕变方程[24-25]并将其嵌入模拟中,分析不同时期下边坡坡体蠕变变形特征,确保未来边坡坡体安全稳定。

1 研究区概况

研究区位于支党河河谷段,地貌单元属黄土梁峁间河谷阶地地貌,区内不良地质现象主要为黄土滑坡、冲沟陷穴、落水洞、人工洞穴和不发育采空区等。多数滑坡距离路线大于40 m,对路线无工程影响,支党河特大桥的主要威胁对象是HP15高边坡,3个桥墩位于滑坡体上。该滑坡周界清晰,后缘滑壁陡立,滑坡体堆积于坡脚,坡脚易受河流冲刷,且坡面汇水面积较大,冲刷严重。图1为HP15高边坡地质剖面。

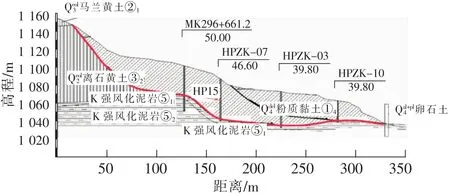
图1 高边坡地质剖面Fig.1 Geological profile of a high slope

2 土体剪切蠕变试验及蠕变模型

试验所用的土样取自咸阳旬邑支党河大桥项目区HP15高边坡开挖面上(图2),试样均为探槽法取得的原状土样,密封后运回,制作成直径61.8 mm,高20 mm的标准试件,土样如图3所示。通过改装后的直剪仪(图4)对原状黄土试件进行室内剪切蠕变试验,以此来对HP15高边坡的变形-时间关系进行研究。

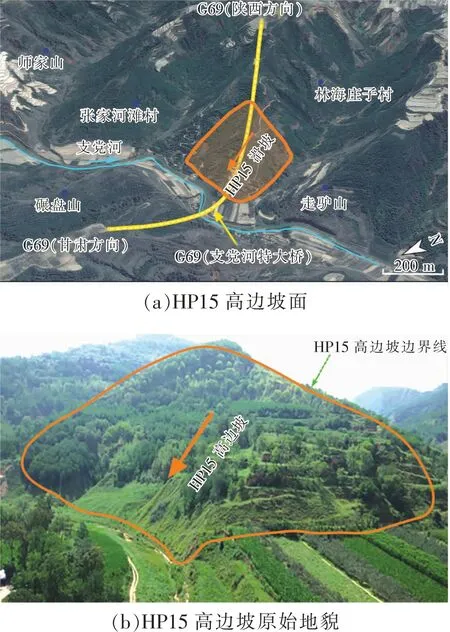
图2 项目区位置Fig.2 Location of the project area

图3 试验试样Fig.3 Test samples

图4 改装后的直剪仪Fig.4 Modified straight shears

2.1 试验方案设计

试样的取土位置距开挖前坡面高差约为40 m,土体天然密度1.64 g/cm3。其土体为Q2离石黄土,土质均匀,结构疏松,具有明显可见的针状空隙,偶见钙质结核,成分以黏粉粒为主,夹杂古黄土壤,古土壤呈团粒结构,结构致密。对原状土试样进行基本物理试验,基本物理指标见表1。

表1 土的基本物理指标

在进行剪切蠕变试验开始之前,需进行天然含水状态下的剪切试验。仪器采用常规的ZJ型应变控制式直剪仪,将正应力设置为100,200,300,400,600,800 kPa来进行剪切试验。因剪切试验并非研究重点,此处仅给出试验所得结果,见表2。

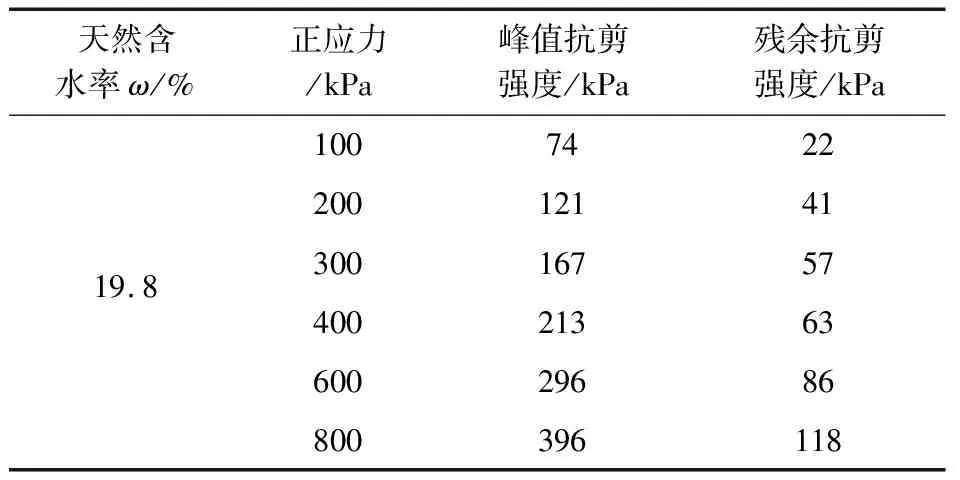
表2 天然含水条件下土的剪切试验

蠕变试验的加载方式一般分为分别加载和分级加载两种,两种试验加载方法各有优缺点,结合实际情况,试验采用分级加载方式。根据取土位置及土体天然密度,试验固结应力以600 kPa为上限,最大固结应力设置为400k Pa。依据“陈式加载法”[26],蠕变剪切试验的剪应力一般取其抗剪强度的0.9倍以下[27-29],试验初始剪切应力设置为最大剪切应力的40%～50%,每级荷载增量为最大剪切应力的8%～10%,实际加载方案见表3。每级加载时间按实际情况而定,待变形稳定后开始下一级荷载施加,试样剪切变形稳定的标准为24 h变形量小于0.05 mm。试验过程中为防止水分散失,在试件上下表面贴上一层保鲜膜,并在剪切盒外围用潮湿的棉花和保鲜膜包裹。

表3 蠕变剪应力加载

2.2 试验结果分析

将每级应力增量引起的变形平移到y轴,再与上一级应力作用下的变形进行叠加,即得到该级应力水平作用下的蠕变曲线。由此可以得到蠕变试验各级加载应力下的分别加载蠕变曲线如图5所示。

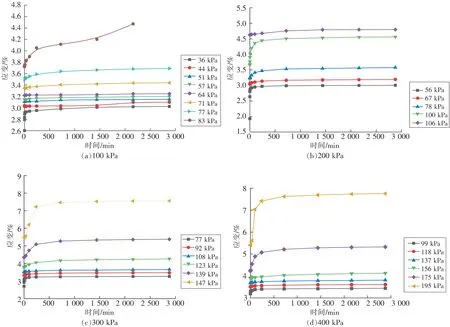
图5 应变-时间曲线Fig.5 Strain-time curves

为了更清晰地描述土体应力-应变关系,通过提取同一时刻各级应力状态下蠕变曲线上的应变值,可获得不同应力状态的应力应变等时曲线,如图6所示。剪切模量是材料剪切应力与应变的比值,它表征材料抵抗剪切应变的能力,文中以蠕变等时曲线斜率的倒数代表“剪切蠕变模量”[30],来更直观的展示试样在蠕变过程中的抗剪切能力,如图7所示。

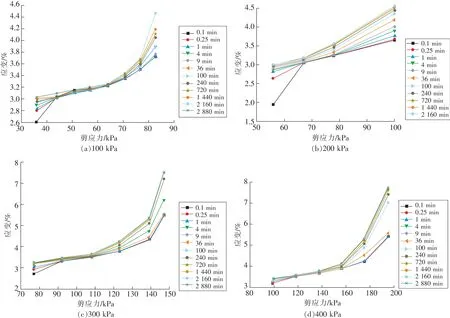
图6 等时应力-应变曲线Fig.6 Isochronic stress-strain curves of different consolidation stresses

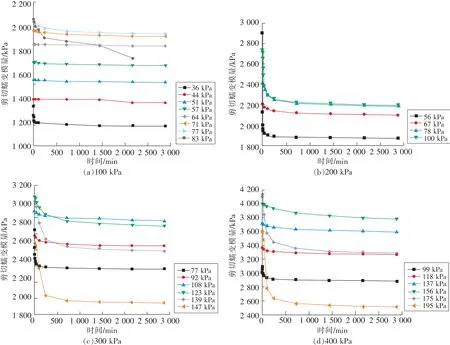
图7 各级正应力作用下剪切蠕变模量随时间变化规律Fig.7 Variation of creep shear modulus with time under different normal stresses

从试验曲线可以看出,各级固结压力下的土样在低剪应力状态下均表现出初始蠕变和等速蠕变。在加载初期试件表现出明显的瞬时应变,随后进入初始蠕变阶段,经较短时间后试件变形达到稳定,应变速率几乎为0,并且随着剪应力的增大,试样进入稳定蠕变阶段的时间就越长,时间效应越明显。

通过分析不同应力状态下试样的等时应力-应变曲线可知,在加载前期变形量较小,曲线呈线性变化,在该阶段试件主要以弹性变形为主。随着时间推移,曲线呈现出明显的非线性关系,试件表现出黏塑性变形。从曲线形态上分析发现蠕变前期等时应力应变曲线均出现重合现象,应变与时间呈渐进趋势,后期逐渐发散,曲线向应变轴偏移,表明试件在整个阶段蠕变速率先减小后增大。

2.3 高边坡黄土蠕变模型

Burgers模型由Maxwell体和Kelvin体串联而成,如图8所示,其中Maxwell体用来模拟瞬时弹性变形和等速蠕变,Kelvin体则模拟初始蠕变。

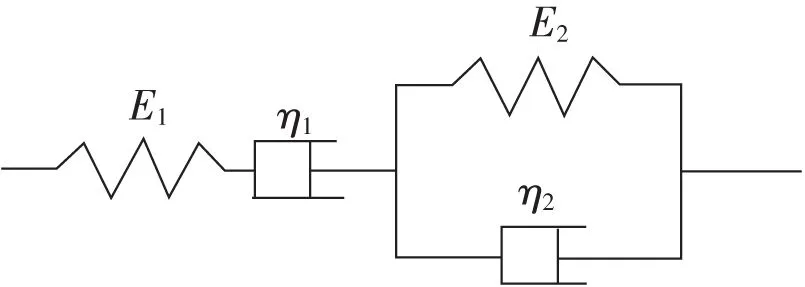
图8 Burgers模型示意Fig.8 Sketch of Burgers model

Maxwell体由一个弹性元件和一个黏性元件串联而成,其本构方程为

(1)

式中η为黏性系数,kPa·min;

根据初始条件t=0,ε=ε0=σ0/E解得其蠕变方程为

(2)

Kelvin体由弹性元件和黏性元件并联而成,其本构方程为

(3)

当t=0时,施加恒定力σ0,由本构方程可得Kelvin体蠕变方程为

(4)

由Maxwell体和Kelvin体串联得到其本构方程为

(5)

利用瞬时叠加原理,将2个蠕变方程叠加,可得Burgers模型的蠕变方程为

(6)

对于剪切蠕变试验而言,由于元件两端施加的是剪应力,故可以得到剪切蠕变应力状态下Burgers一维蠕变模型为

(7)

为便于后期数值模拟土体参数选择,依据所取土样受载等实际情况,选取400 kPa固结应力下试验结果与本构模型进行拟合,得到本构模型参数见表4。

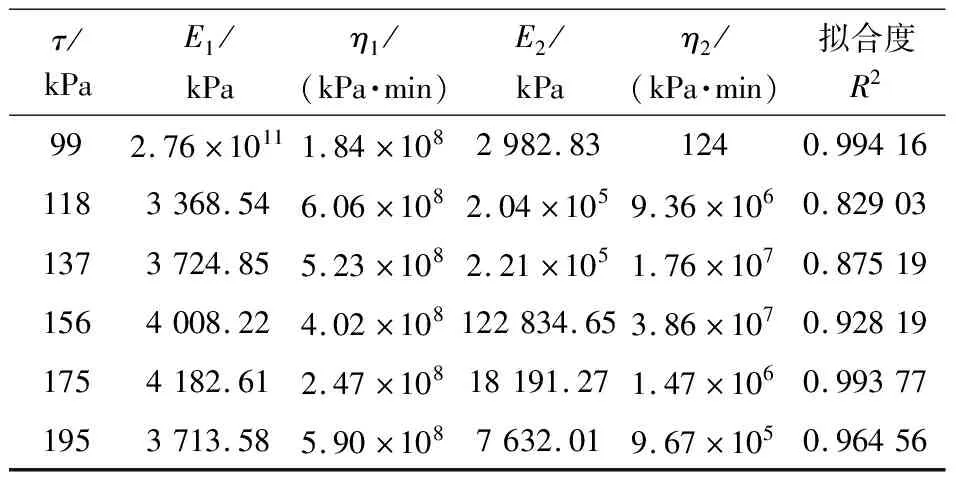
表4 Burgers蠕变模型参数值

3 高边坡稳定性数值模拟

3.1 边坡岩土体数值模型的建立

将HP15高边坡地质剖面图导入FLAC3D(5.01版本)软件中,利用Extrusion进行三维地质建模,对模型的四周和底部进行边界条件的施加,其中左右2个边界施加x向的位移边界条件,前后2个面施加y方向的边界条件,底部施加z方向的边界条件,顶部自由边界。

考虑到边坡的蠕变效应,边坡岩土体本构模型是在Mohr-Coulomb模型的基础上嵌入Burgers流变模型,将蠕变公式及参数写成fish语言,然后加入到FLAC3D计算程序中,通过流变模型建立起与实际时间的关系,并基于Mohr-Coulomb屈服准则,能够较好地体现出土的黏弹塑性。边坡基岩部分整体位移较小,基岩部分采用摩尔库伦模型,并对蠕变模型参数(表5)、岩土体物理力学参数(表6)进行统一取值。

表5 边坡数值模拟参数

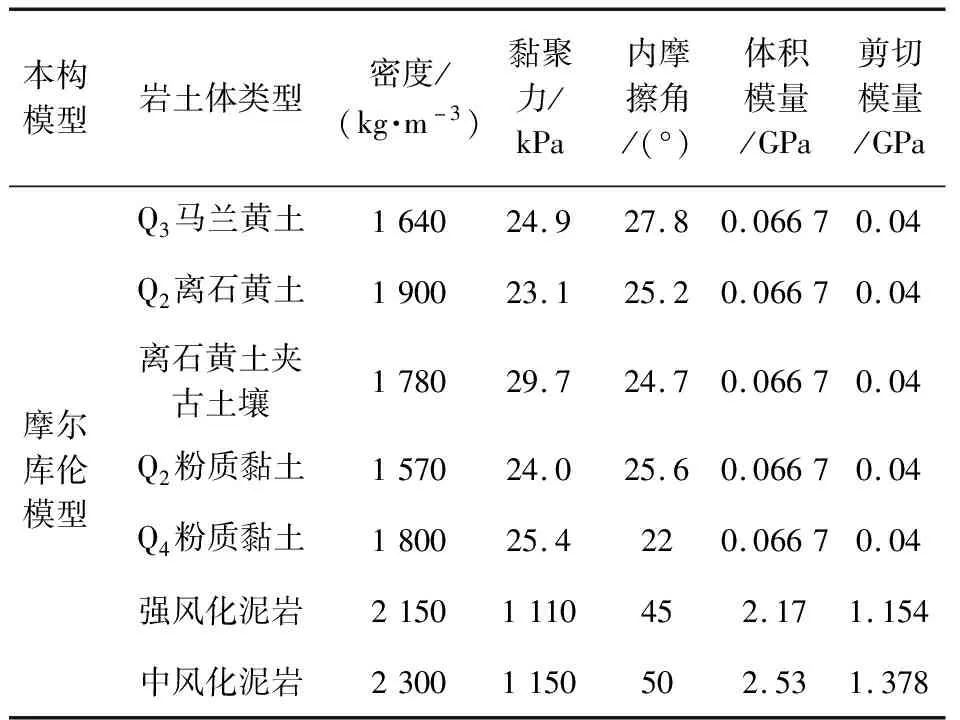
表6 边坡稳定性数值模拟岩土体参数

3.2 数值模拟计算结果分析

3.2.1 边坡开挖前的蠕变分析

1)边坡开挖前的蠕变塑性区云图见图9。塑性区破坏位置先从坡顶开始,既有剪切破坏也有张拉破坏,但蠕变初始时期坡体仅在顶部出现了部分破坏区,在基岩与土体交界位置由于地形陡然下降,在重力作用下形成集中应力,导致出现了破坏区;随着时间延长,坡体表面破坏区越来越多,塑性区持续发展,直至蠕变到30 a,可以初步判断塑性区没有进一步扩散,坡体破坏基本停止。

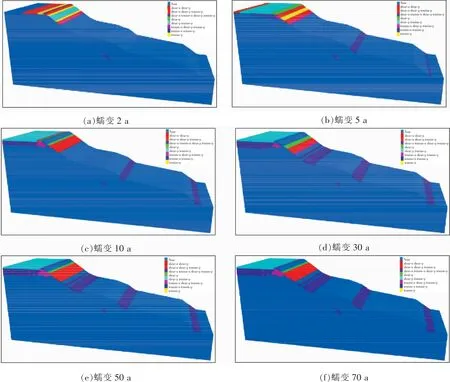
图9 边坡开挖前的蠕变塑性区云图Fig.9 Cloud map of creep plastic zone before slope excavation

2)边坡开挖前的蠕变位移云图见图10,开挖前剖面模型的位移由初始的4 cm增长到蠕变10 a的12 cm,再到蠕变30 a的63.6 cm,之后位移逐渐稳定,可知在这一时间段内坡体已经发生了加速蠕变;位移在30 a到70 a之间只增长了1 cm,说明土体已经稳定。

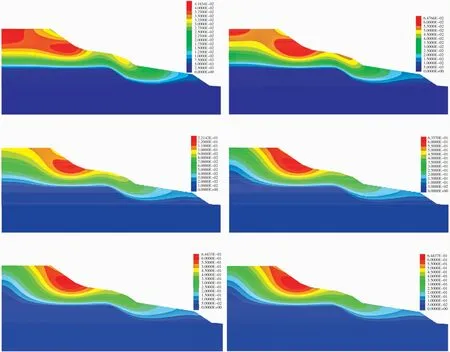
图10 边坡开挖前蠕变位移云图Fig.10 Cloud map of creep displacement before slope excavation

3.2.2 边坡开挖后的蠕变分析

1)边坡开挖后的蠕变塑性区云图如图11所示,开挖后的边坡塑性区在蠕变初始阶段仅存在于坡体中上部位置的表层和由于基岩起伏的原因导致的在坡体中间位置岩土体界面上,该位置塑性区与断面模型的稳定系数与滑动面位置相同,蠕变到5 a时塑性区的发展与蠕变2 a基本相同,到10 a时开挖面底部出现新的塑性破坏区,蠕变发展到30 a时在坡顶表面出现新的塑性破坏区,随后的多年时间坡体塑性区都没有再发生任何变化,表明开挖以后的边坡在10 a和30 a的时间段内达到稳定状态。

图11 边坡开挖后的蠕变塑性区云图Fig.11 Cloud map of creep plastic zone after slope excavation

2)开挖后的蠕变位移云图如图12所示,边坡蠕变2 a时位移总量约为3.3 cm,5 a位移量为3.8 cm,蠕变10 a位移约为6.2 cm,蠕变30 a位移为27 cm,随后的50 a和70 a,位移基本稳定。蠕变初期边坡最大位移发生在坡顶,随后转移至开挖面中下部地形突出位置,可以理解为顶部位移趋于稳定,开挖面中下部位置产生较大的位移,但在10 a和30 a之间达到稳定状态,坡体总位移远远小于开挖之前,证明开挖对坡面稳定大有作用。

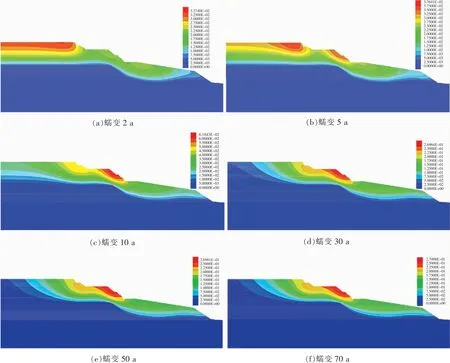
图12 边坡开挖后的蠕变位移云图Fig.12 Cloud map of creep displacement after slope excavation

通过数值模拟结果可得出以下推论:

1)边坡剖面随着上部开挖其稳定系数先从1.5升高到2.05之后降低到了1.84,边坡模型稳定系数都远大于建筑边坡工程技术规范中永久边坡在一般工况下一级安全等级所要求的稳定系数1.35;

2)对开挖前后的各剖面边坡进行了蠕变模拟,结果表明,在开挖之前各个剖面边坡都在较短时间内出现了较大的位移,开挖后位移量大幅度减小,土体开挖对于边坡的稳定性提升明显;

3)开挖以后HP15高边坡依然存在蠕变破坏的问题,需要针对边坡的地形、破坏形式、破坏范围、位移情况进行持续追踪。

3.2.3 讨论与分析

咸阳旬邑支党河大桥项目区HP15高边坡原状土的剪切蠕变试验结果表明,固结应力越小,剪切蠕变模量越小,土的抗剪强度越低,即浅部土体发生蠕变变形难度越小,蠕变位移量越大。数值模拟结果表明未采取开挖治理时,30 a内边坡最大位移量达到63.6 cm,之后位移量逐渐保持稳定。

与以往学者研究相比,在研究室内土体剪切蠕变特性的基础上,建立起土体蠕变本构模型,并将其嵌入到FLAC3D数值模拟软件中,对原状黄土的蠕变模型进行模拟反演,分析不同阶段边坡蠕变变形特征,验证了蠕变试验及数值模拟结果的可靠性,为以后高边坡安全稳定性研究提供依据。

4 结 论

1)通过对原状黄土开展剪切蠕变试验可以发现,蠕变前期各级固结应力状态下的试样等时应力应变曲线均出现逐渐重合的现象,应变随时间增加缓慢,而后期发散,等时曲线逐渐向应变轴偏移,显示了试样蠕变速率先减小后增大,蠕变速率的拐点即为试样长期抗剪强度。

2)通过对高边坡是否开挖治理后2,5,10,30,50,70 a的模拟显示,若不对高边坡采取任何处理措施,高边坡在2 a时虽能保持稳定状态,但在5 a时开始出现坡脚位置的蠕变破坏,10 a时坡顶和坡中将出现严重的滑移破坏,直至30 a高边坡出现整体失稳。而采用开挖方式治理高边坡,第5年出现局部微量破坏,至30 a破坏区域达到最大,但并未形成贯通性滑动面,坡体最大位移量仅为开挖前的42%。因此从经济角度考虑,应采用开挖方式治理HP15高边坡,且采取相应的防排水等防护措施将有利于坡体整体稳定。