基于物理模型建构的解题研究

摘 要：物理解题并不单纯是应用物理知识解决物理问题的过程，而是学生针对问题建构物理模型的过程.因此，教师进行物理习题教学前应分析学生基于模型建构的解题过程，发现学生的问题以采取针对性的教学策略.文章依据Gilbert提出的建模模型分析了学生在物理解题过程中可能出现的模型提取问题、模型表征问题和模型评估问题，同时获得了物理习题教学的两点启示.

关键词：物理模型；模型建构；习题教学

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）29-0061-04

收稿日期：2023-07-15

作者简介：刘雨萌（1991.2-），女，黑龙江省佳木斯人，研究生，中学一级教师，从事物理教学研究.

模型建构能力是一种重要的思维能力，近年来模型建构能力已经被写入多个国家的课程文件中，《义务教育物理课程标准（2022年版）》中也指出，学生要会用所学模型分析常见的物理问题^[1].但实际教学中，很多学生在遇到物理题目时往往感觉无从下手，究其原因是学生无法从物理习题情境中准确构建物理模型.因此，有必要分析和梳理物理习题解决过程中的模型建构活动，从而为物理习题教学提供启示.

1 物理模型建构的内涵

物理模型建构的内涵中包含了两个要素，一是模型建构活动，它往往发生在问题解决过程中，用来简化和整理对物理问题的思考；二是模型建构结果，即物理模型，它是建模者的思维指向，即形成物理对象或物理事件的关键结构，包括空间结构、物理过程、物理属性等，这些关键结构能起到替代物理对象的作用，从而简化思维的工作任务.总的来说，物理模型建构是物理问题解决中的重要思维活动，是建模者在解决物理问题过程中，为了简化物理问题、抓住问题的主要矛盾而在头脑中建立物理对象或物理事件的关键物理过程、物理属性、物理空间结构等的科学思维活动.

2 基于物理模型建构的解题过程

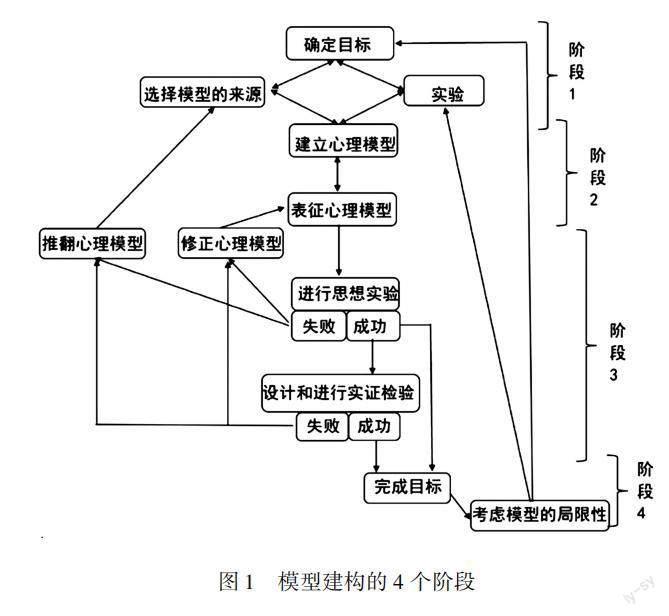
关于模型建构过程的研究在上世纪八十年代已经在国外展开，Hestenes、Clement、Gilbert等研究人员均提出了自己的观点.其中Gilbert和Justi在Clement基础上提出的建模模型是科学课程经常采用的模型之一^[2].他们认为模型建构包括四个阶段，如图1^[3]所示，基于这一过程能够启发我们认识到学生解答物理习题的规律.

根据这四个阶段可知，当学生解答物理习题时，他们首先会一边理解习题一边从记忆中搜索和选择可用的模型素材和经验依据来建立一个关于问题的心理模型；其次，学生会使用合适的表征方式将心理模型表达出来；再次，学生通过反思来评估模型与情境的一致性，并随时进行修改，当学生认为模型符合情境时，就可以应用模型来解答问题；最后学生通过解答习题明确了模型应用范围，从而可以尝试将这一模型迁移到类似的物理习题中，整个过程既是解题活动同时也是模型建构活动^[4].

3 学生基于模型建构的解题案例分析

学生在解题的过程中会由于缺乏模型建构的意识和能力而出现各种问题，下面以三个不同领域的习题为例进行具体分析.

3.1 力学习题案例分析

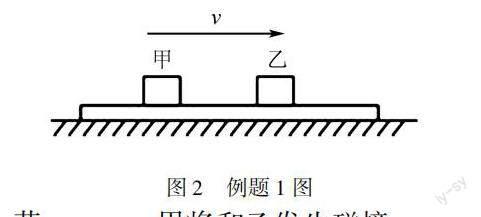
例1 质量分别为m₁、m₂的甲乙两个物体，放在表面光滑且足够长的木板上，随木板一起以水平向右的速度做匀速直线运动，如图2所示，当木板突然停止时，以下说法正确的是（）.

A．若m₁＞m₂，甲将和乙发生碰撞

B．若m₁＜m₂，甲将和乙发生碰撞

C.若m₁=m₂，甲将和乙发生碰撞

D.无论两个物体质量关系如何，都不会碰撞

答案解析 此题考查学生对牛顿第一定律的理解，找出题目中的关键词“光滑”说明物体不受摩擦力，“匀速直线运动”说明物体处于平衡状态，在水平方向上不受力，那么原本运动的物体就会保持原有的运动状态，因此，甲乙两物体都以原有的速度继续做匀速直线运动，此时需要学生在脑海中建构一个“匀速直线运动”的物理模型，那么各自做勻速直线运动的两个物体，速度相同，永远不会碰撞，故此题正确答案D.

基于模型建构的学生解题分析：一些学生会选择A选项，为什么他们会认为如果甲的质量更大就会撞上乙呢？这需要结合学生的模型建构过程进行分析：在学生以往的经验中，由于惯性，质量大的物体不容易停止运动，质量小的物体则相反.因此，他们根据生活经验建立了木板停止后的甲运动将比乙快的错误模型.这说明学生在建立模型时仅根据生活经验而缺少对学习过的模型素材的提取和运用，也就是说，他们并没有正确地提取和运用牛顿第一定律，因此忽略了试题中所包含的“甲、乙水平方向上不受力”的条件，未能建立甲和乙将继续保持匀速运动的模型.

3.2 光学习题案例分析

例2 学过透镜知识后，小明所在实验小组在光学实验室（暗室）想对学过的知识进行深入研究，可用的器材有：光源S（视为点光源）、圆形凸透镜（直径为）、光具座、光屏（足够大）.如图3所示，将光源、凸透镜和光屏放在光具座上，调节高度，使光源和光屏的中心在凸透镜的主光轴上.将光源S置于凸透镜的左焦点处，左右移动光屏，小明发现在移动光屏的过程中，在光屏上光斑外侧还有一个暗环，他猜想可能是凸透镜的边框造成的，于是他拆除边框直接将凸透镜固定在光具座上，进行实验验证，发现暗环仍然存在，你认为暗环是如何形成的？若光源S在左焦点上，光屏在右焦点处，如图4所示，请你算出此时暗环的面积等于多少？

答案解析 此题考查了学生对光经过凸透镜时所走的光路的理解和绘制，如下图5所示：从S发出的光，以A、B为临界点，经过A点之上的沿直线传播到C点之上，同理经过B点之下的沿直线传播到D点之下，而经过A、B两点之间的光经过凸透镜的折射，折射光线的方向平行于主光轴，位于MN之间，因此，没有光照到CM和ND之间，凸透镜是一个圆形的透镜，即形成一个圆形暗环，如下图6所示.故暗环的形成是透镜外侧沿直线传播的光与经透镜折射的光在屏上形成的无光区.暗环的面积即图中的阴影面积，S_阴影=S_大圆-S_小圆，由图6可知，小圆半径等于透镜半径，为?d ，因光屏在右焦点处，故依据相似三角形的知识可知，大圆半径为d，可得S_阴影=S_大圆-S_小圆=πd²-π（?d）²=?πd²

基于模型建构的学生解题分析：对于这个问题很多学生往往感到无从下手，不明白为何透光的透镜会形成暗环.那么学生解题的困难主要是什么呢？结合学生的模型建构过程可知，学生的解题困难很可能出现在他对模型素材的提取和模型的表征阶段.首先，在模型素材的提取阶段，由于用光具座探究凸透镜成像这一情境对学生来说会在学习凸透镜成像规律的内容中遇到，因此学生能够很容易提取光经过凸透镜的光路模型，但光的直线传播模型在这一情境中很容易被学生忽略，这导致学生难以理解外圈的暗环从何而来；其次，在模型表征阶段这一问题需要学生一边绘制光路一边思考，因此学生的另一个困难是他并不知道如何将光路表征出来以辅助他思考问题，比如，虽然学生头脑中提取了一个模糊的包含光要直线传播和光经过凸透镜将会聚的心理模型，但他无法用光路图来表达光在传播到凸透镜边缘时将经过怎样的路线.因此，无法准确表征可能是学生解答此题的另一个困难.

3.3 电学习题案例分析

小明打算只利用电流表来测量小灯泡的额定功率，小灯泡的额定电压为2.5 V，他增加了一个阻值为10 Ω的定值电阻R₀和两个开关，设计了如图7所示电路，请将电阻R₀、电流表和灯泡的符号填入虚线框中以便完成实验.

答案解析 此题考查学生对缺电表电路的设计.器材中没有电压表，因此需要设计用已有器材替代电压表，依据公式U=IR，可以将电流表与定值电阻串联后当作电压表使用，将其与小灯泡并联便可测量小灯泡两端的电压，此时开关S₁断开，S₂闭合，灯的电压即为定值电阻与电流表示数的乘积，由此确定了小灯泡的位置在X，而定值电阻和电流表的位置还需进一步分析.为测得小灯泡的额定功率，第一步要使小灯泡正常发光，调节滑动变阻器，直到电流表的示数为I=U/R=2.5 V/10 Ω=0.25 A时，小灯泡的电压达到额定值2.5 V正常发光，第二步根据P额=U额I额，还需测出此时的电流I额，而为使小灯泡始终正常发光，小灯泡与电阻的连接情况应保持不变，即开关S₁闭合，S₂断开后，小灯泡与电阻仍然保持并联的连接方式，只有定值电阻在Y位置，电流表在Z位置才能够做到，因此电路连接应如图8所示，读出此时电流表的示数I总，I额=I总-0.25 A，故小灯泡的额定功率为P_额=2.5 V（I_总-0.25 A）.

基于模型建构的学生解题分析：缺电表的电路设计一直是学生较为迷茫的一类题目，究其原因一方面学生缺少用已有模型素材构建新模型的能力，在本题中学生无法构建电流表和定值电阻串联的电压表替代模型；另一方面还包括学生模型评估能力较弱，在本题中，一些学生不能从一个假设去推理内部一致的电路模型，比如，假设小灯泡位置正确，在X位置，而定值电阻在Z位置，电流表在Y位置，学生很难从这一电路模型中评估其是否能够测量小灯泡的额定功率，由于学生不能寻找电路模型与问题情境的一致性，导致其无法构建正确的模型.

4 对物理习题教学的启示

4.1 依据模型建构过程系统分析学生的解题困难

根据上述分析可以发现，学生在解题中遇到的困难并不是单一由于某个知识点不理解造成的，而是在学生建构心理模型时的复杂的、多阶段的问题，教师在习题教学时应该结合学生的模型建构过程具体梳理其解题思维、系统分析解题困难.要做到这一点，教师需要了解学生模型建构的一般过程并具有学生常见解题困难的经验积累，在此基础上建构学生解答习题的思维活动，包括思考学生解答习题需要提取哪些生活经验和模型素材，学生需要如何建立和表征模型，学生要如何通过思维实验及批判性反思去验证模型内部及模型与问题情境的一致性，最终学生能够从习题中总结什么模型素材并用于解决新问题.通过这样的梳理教师就能够结合每个学生的解答情况具体分析其解题困难出现在哪个阶段，具体方法可通过评价学生解答结果、对比不同学生的答案、观察学生课堂反馈和针对结果进行访谈等.

4.2 针对学生在解题中的模型建构问题设计应对策略

掌握了学生解题过程中建构模型的具体问题，就能据此设计针对性的教学策略.一是，对于学生模型提取阶段的问题，教师应鼓励学生运用物理语言和生活经验解释问题情境，引导学生建立物理概念、经验直觉同问题情境间的联系^[5]；二是，对于模型表征阶段的问题，教师应该引导学生用多种方式清晰地表达和解释想法，尽量用可视化的方式辅助模型建构思维^[6]；三是，对于模型反思阶段的问题，教师应引导学生尝试用多个模型匹配情境，训练学生运用如果……那么会发生……的思维实验去推理不同模型与问题情境是否适配，以发展对模型一致性的評估能力；四是在模型总结与迁移阶段，教师不是单纯的进行知识点总结，而是从基于模型建构的解题过程进行系统的总结，比如总结情境与模型间常见的关联是什么，某一类问题常用的表征方式是什么，模型与情境的一致性思考途径是什么，等等，这些是学生进行习题迁移的重要思考工具和基础.

总的来说，学生在解题过程中并不单纯是知识的运用，而是基于自身的经验和模型素材对情境中的问题进行的模型建构过程.在新课程背景下，教师对物理习题的理解和教学应跳出简单的内容教学的限制，从更复杂的思维与知识的关联出发，系统分析解题困难、设计教学策略，最终提升学生的物理学科核心素养.

参考文献：

[1] 中华人民共和国教育部.义务教育物理课程标准（2022 年版）[M].北京：北京师范大学出版社，2022.

[2] 张静.基于心智模型进阶的物理建模教学研究[M].南宁：广西教育出版社，2020：69.

[3] Justi R S， Gilbert J K.Modelling， teachers' views on the nature of modelling， and implications for the education of modellers[J].International Journal of science education， 2002， 24（4）：369-387.

[4] Gilbert J K， Justi R.Modelling-based teaching in science education[M].Cham， Switzerland： Springer international publishing， 2016.

[5] Cheng M F， Brown D E.Conceptual resources in self‐developed explanatory models： The importance of integrating conscious and intuitive knowledge[J].International Journal of Science Education， 2010， 32（17）： 2367-2392.

[6] Gilbert J K， Justi R. Modelling-based teaching in science education[M].Cham， Switzerland： Springer international publishing， 2016.

[责任编辑：李 璟]