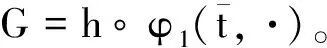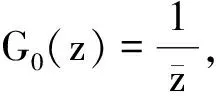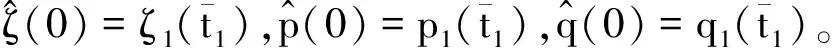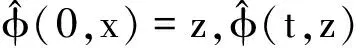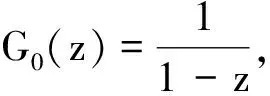SLE(κ,ρ)的可逆轨迹
2023-11-02梁静
安阳师范学院学报 2023年5期
梁 静
(淮南师范学院 金融与数学学院,安徽 淮南 232001)
0 引言

1 预备知识
在这一节中给出涉及的一些定义、记号以及一些基本事实,更详细的请参见文献[7-10]。
令φj(t,·),K(t)(0≤t 对于0≤t 那么Bj(t)(0≤t 令D={(t1,t2)∈[0,T1)×[0,T2:γ1([0,t1]∩[0,t2]=φ)},那么对于任意(t1,t2)∈D,K1(t1)∪K2(t2)是H上的一个壳。且对于任意(t1,t2)∈D,令 Kκ,tj(tκ)=(Kj(tj)∪Kκ(tκ))/Kj(tj) =φj(tj,Kκ(tκ)) 且φκ,tj(tκ,·)=φκ,tj(tκ)。在D定义Aj,h,Bj,0(h∈Z)为 Bj,0(t1,t2)=φκ,tj(tκ,pj(tj)) 令Ej,0=Aj,0-Aκ,0=-Eκ,0≠0,Ej,m=Aj,0-Bm,0,m=1,2。 (1) (2) (3) (4) 故 (5) (6) ζ(t) (7) 因而 (8) 注意到E1,0=-E2,0。 (9) (10) 由(9)(10)得 (11) (12) 令 (13) (14) 由(2)(3)(4)可得 由(13)有 =S(t) q(t)-ζ(t))dt,0 (15) 定理2γ1(0,T1)=γ2(0,T2)2 SLE(κ,ρ)的可逆轨迹