降雨环境下电磁波短距离传播衰减研究

王 敏，任俊峰，周云林

降雨环境下电磁波短距离传播衰减研究

王 敏1，任俊峰2，周云林1

（1 中国电子科技集团公司第二十研究所，西安 710068；2 西安机电信息技术研究所，西安 710065）

随着无线电技术的不断革新，在降雨等复杂环境下由于电磁波传播特性变化造成对武器系统的影响逐步被重视。与以往降雨环境下的远距离电磁波传播研究不同，着重阐述了近距离传播过程中电磁波的衰减问题。通过电磁仿真软件的帮助，根据层状云降水情况建立仿真模型，模拟多个频段下电磁波短距离传播过程，并通过计算路径前后电磁波能量差值以反映出电磁波衰减情况。结果表明，在降雨环境中，短距离的电磁波传播由于雨滴的影响，存在较大的衰减，随着频率和传播距离的增加，电磁波的衰减也在增加。

雨衰；降雨环境；短距离传播

0 引言

随着无线电技术的迅猛发展，电磁波迅速融入到人们的生活之中。人们对于电磁波传播过程的研究随着现代科学技术的高速发展也在不断深入，对于复杂环境下电磁波传播特性变化造成系统影响的研究也逐步受到重视。降雨作为一种常见的自然现象，雨滴颗粒对电磁波能够产生吸收和散射等效应，在传播过程中起到了不可忽视的影响。早在 20世纪40年代，J.W.Ryde等人就对雨介质的电磁波传播和散射特性做了大量的研究工作。从那个时候开始，许多学者对气象粒子的传播和散射特性进行了大量的研究。在早期的研究中，一般会把雨滴看作球形，然后利用经典的MIE（Mie scattering）散射计算方法来研究雨滴的散射特性[1]。后来，随着研究的深入，雨滴会被当做扁椭球和底部有凹槽的扁椭球进行研究。各种各样的计算方法也随之产生，其中应用比较广泛的有：点匹配法、Fredholm积分方程方法、T矩阵方法[2]和分离变量法等。降雨环境对电磁波的衰减相关研究已经发展了很多年，但大部分研究重心均在远距离（千米级）电波传播上，并基于不同的雨滴分布给出了降雨所引起的电磁波衰减公式，对于电磁波在降雨恶劣环境下近距离（米级）的传播问题没有一个很好的研究。本文主要围绕电磁波在降雨环境下，对近距离传播过程中的衰减问题开展了相关工作。

1 理论介绍

1.1 雨滴的几何建模

雨滴的尺寸大小影响了雨滴的几何形状，进而会影响其对电磁波的散射特性。在对雨滴散射特性的研究初期，很多研究者将其作为球形目标来模拟。但根据高速摄像研究表明，仅有在雨滴直径不超过0.25 mm时，才可以被当作球形目标来模拟。最小的雨滴尺寸与云中的微小水滴尺寸相当，而最大的雨滴半径也不大于4 mm，因为半径大于4 mm的雨滴处于不稳定的状态，会发生破裂，因此，雨滴的半径通常在0.25～4 mm之间。其形状受到重力和向上的气流作用，通常呈现为底部扁平的椭球体[3]。

自1971年Pitter和Pruppacher[4]使用立式风洞得到了不同尺寸雨滴的长轴比以来，对雨滴形状的研究开始快速发展，直到1987年Beard K V和Chuang C两位学者用一种非线性方程表达式，很好地描述了雨滴的形状[5-8]。Beard和Chuang（以下简称为BC模型）给出了描述雨滴截面形状的极坐标方程式为

由此可以得到雨滴几何外形随尺寸大小所改变的趋势如图1所示[9]。

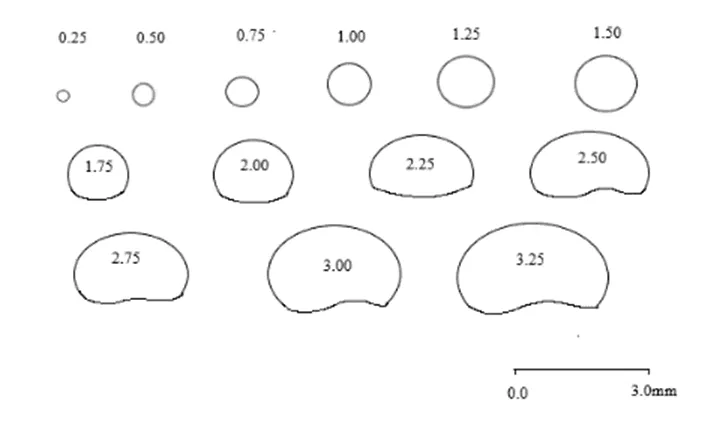
图1 BC模型下雨滴形状随尺寸的变化

从图1中可以清晰地看出，随着雨滴尺寸的改变，雨滴形状从球体变化为扁平的椭球体。当尺寸继续变大时，扁平椭球体底部会形成凹槽，旋转轴近似垂直，形状较为复杂。但1999年姜胜勇在其论文中提出：在电磁波传输过程中，表征雨滴参数的不是其形状，而是其短轴与长轴的比值/[10]。因此在计算中，雨滴椭球模型不考虑其底部凹槽，并用短轴与长轴的比值/和等效球体半径0来表示雨滴的形状大小。其中扁椭球形雨滴的轴比/与等效球体半径0的关系为[11]

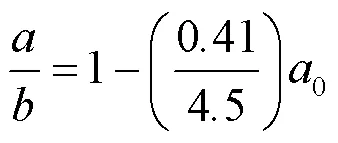
为了方便研究整个降雨路径上的电磁波衰减，在实际研究中通常采用椭球形雨滴，同时椭球形雨滴能够与真实雨滴很好地近似，所以本文也采用椭球形雨滴进行仿真研究。不同等效球体半径下对应的轴比大小如表1所示。

表1 不同等效球体半径下对应的轴比大小

1.2 雨滴谱

对于真实的雨场环境，不仅需要完善单个雨滴的几何建模，还需要了解不同大小的雨滴在空间中是如何分布的，这样才能准确地分析电磁波传播过程中整个雨介质的影响。因此，研究人员引入了雨滴谱的概念，即不同大小的雨滴在相应的降雨率下的空间分布。最早的雨滴光谱测量是Wiesner在1985年使用“吸附纸法”[12]获得的。随着测量仪器和测量方法的发展，越来越多的雨滴光谱模型得到了广泛的测量，如Laws-Parsons分布、Marshall-Palmer分布、对数正态分布、Gamma分布和Weibull分布等，更常用的是Marshall-Palmer分布雨滴谱（以下简称M-P雨滴谱）和Gamma分布雨滴谱。M-P雨滴谱可以表示如式（3）所示

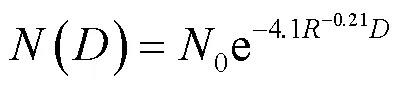
当>0时，分布曲线向上弯曲，当<0时，分布线向下弯曲。研究表明[13-14]，当降雨稳定时，M-P雨滴谱最符合实际情况，但当降雨波动较大时，它不能准确地代表实际情况。Gamma雨滴谱可以准确匹配各种情况下的降雨量，尤其是小雨滴段的雨滴谱拟合效果最好。

2 仿真结果

根据对相关问题的介绍，分析电磁波通过大小不同雨滴的传输问题。以等效球体半径为3.0 mm为例，此时由表1可知，对应的椭球体轴比应为0.72，不妨取雨滴短轴为2.88 mm，长轴为4 mm时，则雨滴模型如图2所示。

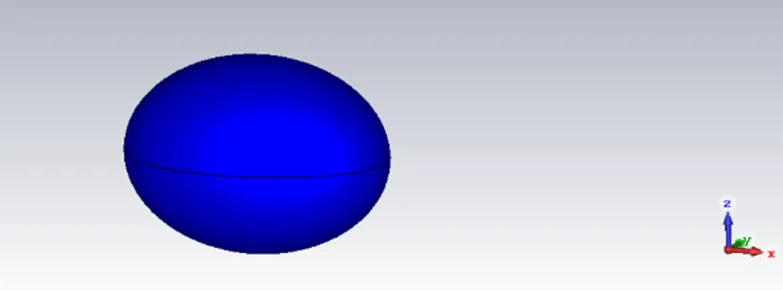
图2 椭球形雨滴模型

事实上，由前述分析可知，此时表征毫米波雨滴特性的是轴比，因此，只要满足等效半径按表1所对应的轴比，即可用来建立相应雨滴尺度下的雨滴模型。雨滴材料选取水的电磁参数以debye模型来近似，以此用来模拟雨滴模型。

由上文可知，雨滴粒子最大半径一般不会超过4 mm。在仿真过程中，将雨滴大小分别等效为半径0.5 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm、3.5 mm和4.0 mm的球体。

以降雨量为50 mm/h为例，不同大小的雨滴粒子在单位体积内随机分布。为缩短仿真计算时间，提高计算效率，选取平面内截面积为1 m2的空气空间，长度在10 m范围内变化的仿真模型如图3所示。在这种假设条件下，由M-P雨滴谱计算得知每平方米空气空间中随机分布着4437个雨滴颗粒，由此来模拟在此条件下的降雨环境。

图3 雨场计算模型

在口径面上设置波导端口，通过仿真计算电磁波在雨介质中的传输过程，仿真分析电磁波在短距离传播过程中由于传播路径中存在雨滴引起的损耗。通过出射端口和入射端口电波功率的比值来表征雨衰，如式（7）所示

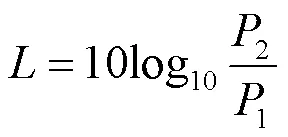
式中：2为出射端口功率；1为入射端口功率，在无雨状态下，该衰减应为0。

本文分别分析了在雨场中电磁波传播2 m、3 m、4 m、5 m、6 m、7 m和8 m时，由于雨滴引起的电磁波衰减，同时，也对比了不同频率电磁波的衰减变化情况，其结果如表2所示。在仿真分析中，考虑到雨滴分布的随机性，每组仿真结果均为20次仿真的统计均值。

表2 特定频率下不同距离的衰减L（×10-2 dB）

根据仿真数据得出的雨衰随频率变化曲线及雨衰随传输距离变化曲线如图4和图5所示。

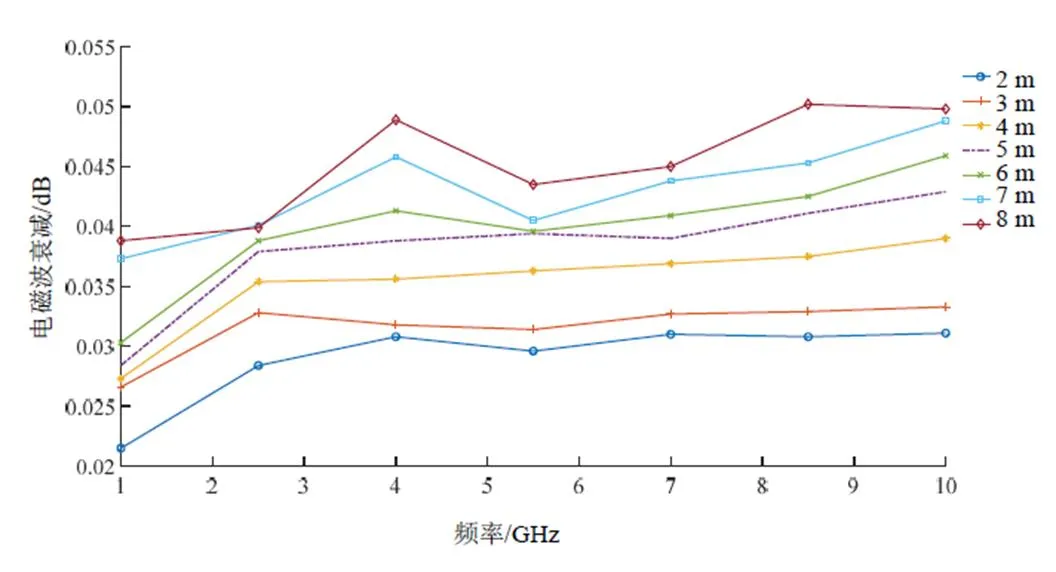
图4 雨衰随频率变化

图5 雨衰随传输距离变化

从表2、图4和图5可以看出，短距离下的电波传播变化趋势与长距离的路径衰减随频率变化趋势类似。短距离时，随着频率的增加，电磁波波长越小，雨滴对于电磁波传播的影响越发强烈；同时，随着电磁波频率及传输距离的增加，雨滴对于电磁波的衰减也在逐渐增大。需要注意的是，本文的研究目标是雨场对电磁波的衰减特性，因此，在本文的仿真中已排除了路径引起的自由空间衰减，仅保留了雨滴引起的电磁波衰减，不同传输距离引起的雨衰，也仅仅考虑了不同传输距离中雨滴对电磁波的衰减。

3 结语

本文通过对椭球型雨滴的建模，结合雨滴谱建立了特定雨量时的随机雨场模型，用来模拟电磁波传播的降雨环境。通过计算电磁学的方法分析了电磁波在路径上遭遇不同分布雨场中雨滴后的能量衰减，用以表征短距离的雨衰。可以看出，随着频率和传输距离的增加，衰减也在增大。虽然按照长距离衰减模型，10 m的衰减几乎可忽略不计，但对于精确制导、精确成像等应用，通过本文的仿真分析表明，即使是短距离传输，雨场的衰减也是不可忽略的，该衰减于雨场分布、雨滴形状和数目、电磁波频率等参数都有着密切关系，需要针对具体应用场景进行精确分析。

[1] 江长荫. 均匀圆球对平面波的散射[J]. 电波科学学报，1996，11（3）：65-88.

[2] P.C.Waterman. Symmetry，Unitary and geometry in electromagnetic scattering[J]. Phys. Rev. D，1971（3）：825-839.

[3] 刘西川，高太长，秦健，等. 降雨对微波传输特性的影响分析[J]. 物理学报，2010，59（3）：2156-2162.

[4] Pruppacher H R，Pitter R. A semiempirical determination of the shape of cloud and raindrops[J]. J Atmos Sci，1971，28：86-94.

[5] Beard K V，Chuang C. A new model for the equilibrium shape of raindrops[J]. J Atmos Sci, 1987，44（11）：1509-1524.

[6] Beard K V，Feng J Q，Chuang C. A simple perturbation model for the electrostatic shape of falling drops[J]. J Atmos Sci，1989，46：2404-2418.

[7] Chuang C，Beard K V. A numerical model for the equilibrium shape of electrified raindrops[J]. J Atmos，Sci，1990，47：1374-1389.

[8] Beard K V，Bringi V N，Thurai M A. A new understanding of raindrop shape[J]. Atmos Res，2010，97：396-415.

[9] 王海军. 复杂降雨条件下极化电磁波传播特性研究[D].北京：国防科学技术大学，2015.

[10] 姜胜勇. 降雨电磁环境特性对雷达性能的影响[D]. 西安：西安电子科技大学，1999.

[11] 朱超. 降雨的毫米波散射及对多普勒引信的影响研究[D]. 西安：西安电子科技大学，2010.

[12] T. Oguchi. Electromagnetic wave propagation and scattering in rain and other hydrometeors[J]. Proceedings of the IEEE，1983，71（9）：1029-1077.

[13] 陈德林，谷淑芳. 大暴雨雨滴平均谱的研究[J]. 气象学报，1989，47（1）：124.

[14] 陈万奎，严采蘩. 雨滴谱及其特征值水平分布的个例分析[J]. 气象，1988，14（1）：8-11.

Study on Short-Distance Propagation Attenuation of Electromagnetic Wave Under Rainfall Environment

WANG Min, REN Junfeng, ZHOU Yunlin

With the continuous innovation of radar technology, both civilian and military radars are demanding more and more accuracy in complex environments. Different from previous studies on long-distance electromagnetic wave propagation under rainfall environment, the attenuation of electromagnetic wave in the short-distance propagation process is focused on. With the help of electromagnetic simulation software, a simulation model was established according to the precipitation situation of stratoid cloud in Henan Province to simulate the short–diastance propagation process of electromagnetic wave in P-band, and the electromagnetic wave attenuation was reflected by calculating the difference of electric field energy before and after the path. The results show that the attenuation of electromagnetic wave increases with the increase of frequency under the same distance propagation of rainfall environment, which is the same as the attenuation trend of long-distance propagation, and the attenuation degree cannot be ignored under the conditions of precision guidance.

Rain Attenuation; Rainfall Environment; Short-Distance Propagation

TN011

A

1674-7976-(2023)-05-387-04

2023-08-18。

王敏（1988.05—），山西静乐人，硕士，高级工程师，主要研究方向为天线与微波技术。