基于分布调幅法的钢框架结构主余震易损性分析

羌鑫楠， 范存新

（苏州科技大学 土木工程学院，江苏 苏州 215011）

约89%的地震（以下称主震）发生后，会在较短的时间内出现二次地震（以下称余震）[1]。 由于主震发生后，余震到来的时间会非常短，这会在一定程度上造成主震发生后损伤结构未及时处理，以及人员尚未安全撤离即遭受到余震。 例如，2010 年9 月，新西兰南岛西部发生里氏7.4 级主震，虽然主震中无人员伤亡，但是在随后的余震中却导致181 人遇难。 2011 年3 月，日本发生了里氏9.0 级主震后，紧接着发生了50 多次余震，没有发生倒塌破坏的损伤建筑结构在余震作用下加重损伤，造成结构倒塌破坏。 然而，在结构抗震设计时，《建筑抗震设计规范》[2]忽略了余震对建筑结构损伤的影响， 使设计人员进行抗震设计时出现一定的误差，可能导致未来地震中更多人员伤亡及结构损伤加重。 因此，研究主震加余震（以下称主余震）对结构的影响具有重要的意义及必要性。

国内外研究人员主要是从以下两个方面对主余震进行研究。 第一个方面是主余震序列构造方式对结构的影响。 例如，Li[3]以钢框架结构为研究对象，对其进行主余震易损性分析，采用人工构造主余震序列与真实主余震序列进行结构抗震性能对比，发现采用人工构造主余震序列评估结构的抗震能力时会偏低；于晓辉[4]分别采用重复法、随机法和衰减法构造的人工主余震序列，对非线性单自由度体系进行增量损伤分析，认为采用重复法或者随机法制造的主余震序列会在一定程度上高估余震对结构损伤，而衰减法制造的人工主余震与之相反，会低估结构损伤影响。 第二个方面是主余震序列下不同结构的易损性分析，如Raghunandan[5]对钢筋混凝土框架结构进行主余震易损性分析，认为余震易损性在各极限状态下的失效概率会随着主震后结构受损严重程度的提高而增长；赵春风[6]以核岛厂房结构为研究对象，研究主余震谱加速度比对核岛厂房结构易损性的影响，认为核岛厂房在各极限状态下的超越概率随着主余震谱加速度比值的增加而增大。

虽然不少学者围绕主余震序列方面的问题展开了研究，然而进行结构易损性分析时，仍存在以下问题值得进一步探讨：（1）多数学者仅采用主震强度或主震及单一余震强度进行构造，未能使主余震序列中主震与余震强度进行独立分析，导致研究余震对结构影响时不够全面；（2）多数学者仅从易损性曲线的角度对结构进行安全性评估，导致结构易损性分析结果缺乏合理性验证，使分析结果存在一定的片面性。

基于上述，本文以钢框架结构为研究对象，采用分布调幅法对主余震序列进行调幅，并从易损性曲线及易损性指数两个角度进行结构主余震易损性分析。 分布调幅法就是将主震及余震分布调幅，分别获得相同主震下不同余震强度的主余震序列，以该主余震序列作为地震动输入可以解决相同主震中余震对结构影响研究不够全面的问题；易损性曲线是从结构极限状态的角度对设计结构进行安全评估，而易损性指数是从结构破坏状态的角度对结构进行安全评估，以该两种方式同时对结构进行主余震易损性分析可以解决易损性分析结果片面性的问题。 相关研究结论的获取，能够全面评估不同余震强度下结构的安全性，为结构设计及评估提供更详细的资料数据及参考依据。

1 有限元模型及主余震序列

1.1 有限元模型

1.1.1 工程概况 以某高层钢框架办公楼为研究对象，根据《钢结构设计标准》[7]进行设计。 该钢框架结构为3 跨12 层，跨度6 000 mm，开间5 000 mm，层高均为3 000 mm。 采用Q345H 型钢梁，其中边跨梁截面尺寸为H600 mm×300 mm×40 mm×50 mm，中跨梁截面尺寸为H500 mm×250 mm×30 mm×40 mm；采用Q345 箱型柱，截面尺寸为500 mm×50 mm；采用混凝土板，厚度为100 mm，混凝土板内钢筋采用HRB335。 该结构按8度抗震设防烈度进行设计，设计地震分组为第1 组，场地类别为Ⅱ类，设计基本地震加速度为0.20g。 见图1。

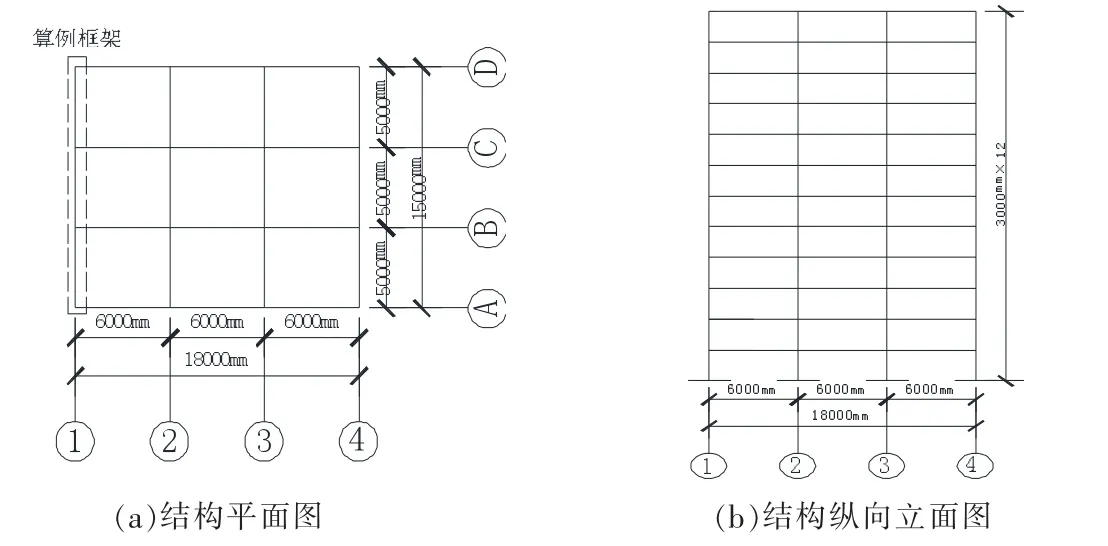
图1 钢框架结构平面、立面图

1.1.2 有限元模型验证 根据1.1 节及下面1.2.1 所述信息，建立有限元模型。 参考论文中验证模型准确性的方法[8]，分别使用Abaqus 及Sap2000 有限元软件对钢框架结构进行模态分析，验证模型的合理性。 由于高阶振型对结构的影响较小，故仅考虑前两阶振型，如图2 与图3 所示。

图2 钢框架结构在Abaqus 软件下的前二阶振型图

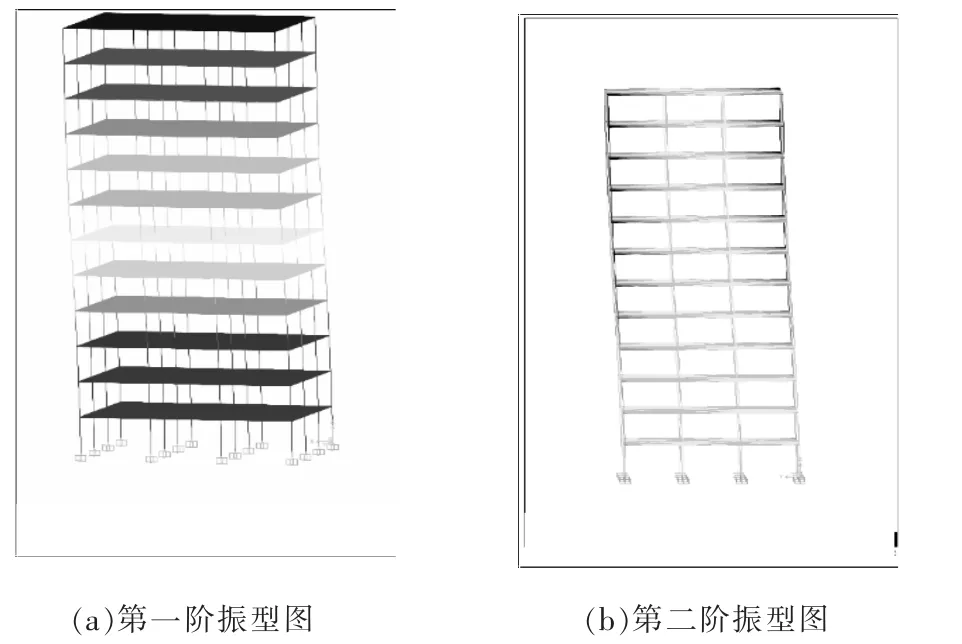
图3 钢框架结构在Sap2000 软件下的前二阶振型图

分析图2 与图3，将两种软件下钢框架结构的固有频率汇总，并进行误差计算，如表1 所列。

表1 钢框架结构固有频率对比表

由表1 可知， 前两阶自振频率计算结果误差最高为0.58%， 说明两种软件下该模型的动力特性基本吻合,证明了钢框架结构模型可用。

1.2 主余震序列

1.2.1 主余震序列挑选及构造 PEER（Pacific Earthquake Engineering Research Center）网站提供了世界各地大量的地震数据记录。笔者从PEER 网站中选用10 条主余震序列，选用的地震为Chi-Chi 地震，主震震级均为7.62，余震震级均为6.3，相应的PGA 如表2 所列。

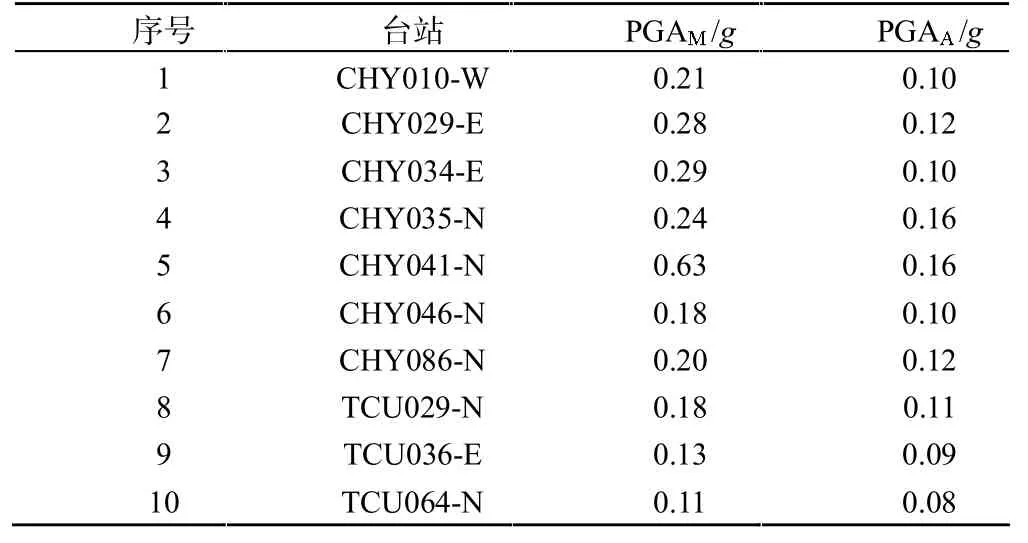
表2 Chi-Chi,Taiwan 地震波信息

选取主余震序列时采用以下原则[9]：台站中存在大于5.0 级的余震；台站中地震峰值加速度（peak acceleration，PGA）的几何平均值要大于0.03g；台站具有完备的剪切波速资料；地震动均记录于场地表面或者底层结构首层。 为确保结构在主震损伤后有足够的时间恢复到静止稳定状态，在主震及余震之间加入10 s 间隔，如图4 所示（PGAM 表示主震PGA；PGAA 表示余震PGA）。 表2 中主余震序列均采用主震及余震直接连接，可以获得10 条如图4 类似的主余震序列。

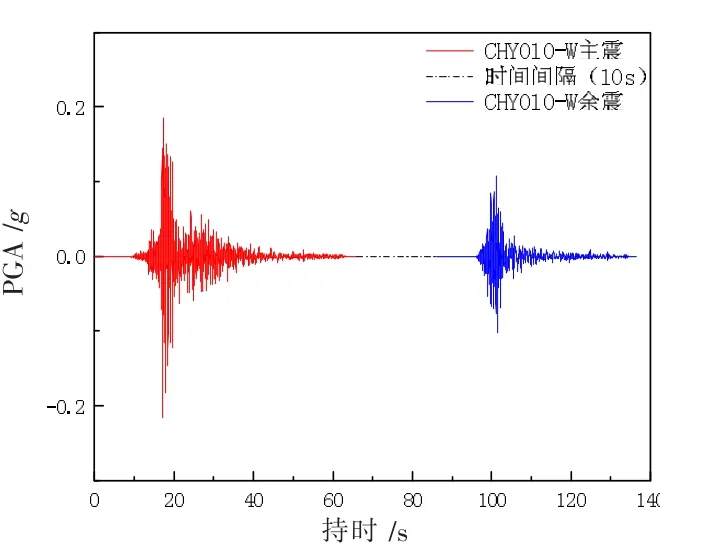
图4 主余震序列构造（直接连接）

1.2.2 地震波调幅 基于小节1.1.1 地震波选取的初始地震波，根据式（1）对结构进行幅值调整。

式中，A'（t）表示调整后的加速度曲线，A（t）表示调整前的加速度曲线；Amax表示调整前的PGA；A0表示目标PGA。

根据《建筑抗震设计规范》[2]中表5.1.2.2 要求，将所选取的地震波分别调幅0.1～1 g。 为进一步研究不同余震强度对结果的影响，将余震按照不同余震幅值比（以下图、表中均采用▽PGA 代替）进行调幅，取值为0.5、0.7、0.9、1。 以CHY010-W 为例，将主余震序列调幅至0.4g，如图5 所示。

2 基于分布调幅法的易损性曲线

2.1 易损性曲线函数

结构需求参数（Demand Parameter，D）与地震动参数关系满足指数关系[10]，见式2。

式中，D 代表地震动需求参数，IM 表示地震动参数；α、β 表示地震概率需求模型系数。

根据HalukSucuogˇlu[11]对地震动潜在破坏势进行卡方拟合优度检验研究成果，D 与地震能力（Capability，C）一般可以假定服从对数正态分布，结构的失效概率[10]（Probability of Failure，Pf）如式3 所示。

可取0.5（根据规范HZUS99[12]，进行易损性曲线求取时，以PGA 为自变量）。

2.2 基于不同余震幅值比下的易损性曲线

2.2.1 不同余震幅值比下地震概率需求模型 按1.2.2 节中调幅的主余震序列输入结构进行时程分析，获得不同余震幅值比下的最大层间位移角（Maximum interlayer displacement angle）θmax。 本节用不同的限定值将钢框架结构划分为五种不同的极限状态[13]。 基本完好与轻微破坏下的极限状态用LS1，轻微破坏与中等破坏下的极限状态使用LS2表示，中等破坏与严重破坏下的极限状态使用LS3表示，严重破坏与倒塌下的极限状态使用LS4表示。 损伤指数取值划分如表3 所示。 不同余震幅值比下主余震序列的损伤指数分布与钢框架θmax回归分析如图6 所示。

表3 损伤指数范围与损伤破坏等级对应关系[13]

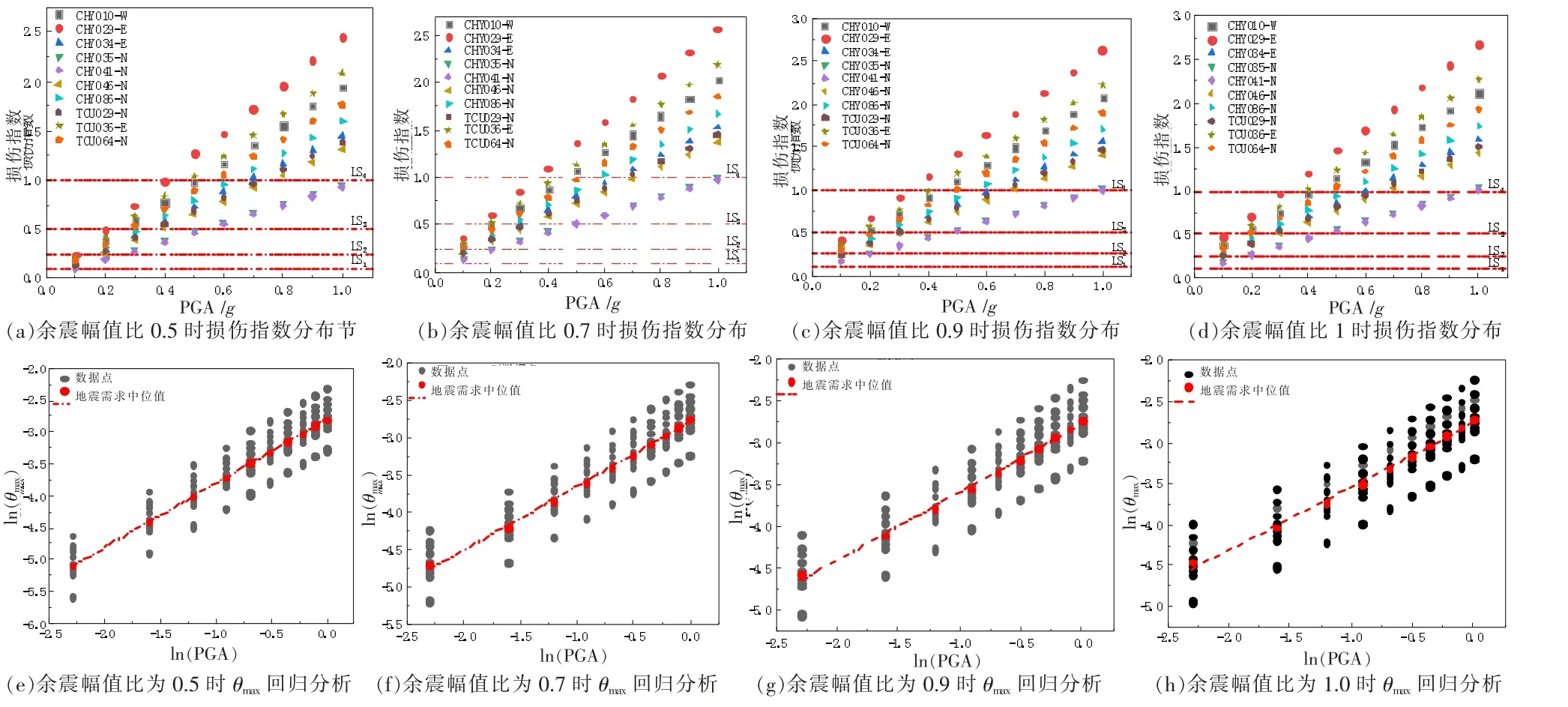
图6 基于不同余震幅值比下损伤指数分布与钢框架θmax 回归分析

将图6（a）～（d）进行损伤指数数量统计，观察不同余震幅值比下结构损伤分布情况，如表4 所示。

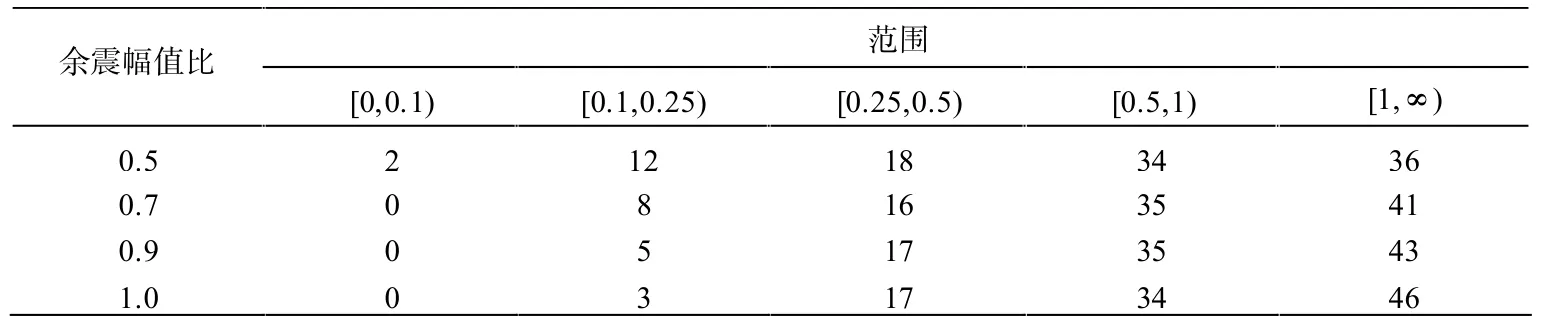
表4 不同余震幅值比下损伤指数数量统计

由表4 可知，在[0,0.5）之间损伤指数数量随着余震幅值比的增大而减少，而[0.5,∞）区间内的损伤指数数量随着余震幅值比的增大而增大。 出现该变化趋势的主要原因是余震幅值比增大，造成余震强度增大，导致相应的主余震损伤指数增大，所以在损伤指数[0,0.5）中的数量会越来越少，而[0.5,∞）中的数量会越来越多，结果表明余震强度的提高会增大结构的损伤指数，使结构损伤进一步加重。

据图6（a）～（d）对结构进行不同余震幅值比下钢框架θmax回归分析，如图6（e）～（h）。 拟合出式2 中α、β系数，得到不同余震幅值比下的地震概率需求模型，相应的拟合系数如表5 所示。

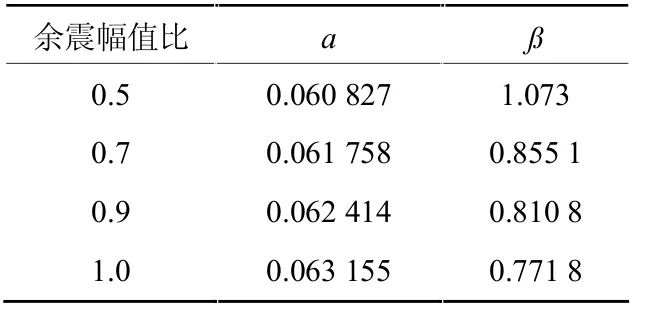
表5 模型系数统计

由表5 可知，D 与IM 指数关系曲线会随余震幅值比值的提高而变陡，表明余震强度的提高会加速增大结构损伤值。 主余震概率需求模型代入式（2）即可。

2.2.2 基于不同余震幅值比下易损性曲线 绘制易损性曲线前需对上述图6 损伤指数进行损伤指数正态分布验证。若X 服从对数正态分布，则变量X 的中值对数值应等于lnX 的均值[14]，见图7。

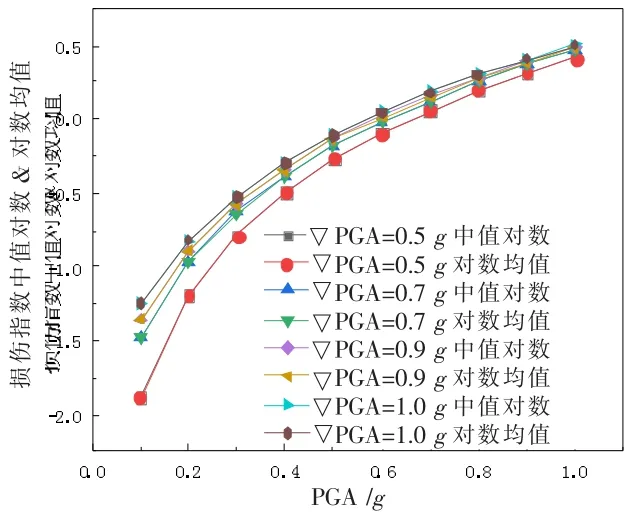
图7 中值对数& 对数均值对比

由图7 可知，不同余震幅值比下损伤指数中值对数与对数均值曲线基本重合，表明损伤指数服从正态分布。 因此可采用式3 进行不同地震强度下失效概率计算，采用表3 中不同破坏限值，绘制不同余震幅值比下结构易损性曲线，如图8 所示。 基于图8，计算结构在各极限状态下的失效概率，研究相应的易损性曲线，不同余震幅值比下主余震较主震失效概率增长值如表6 所示。

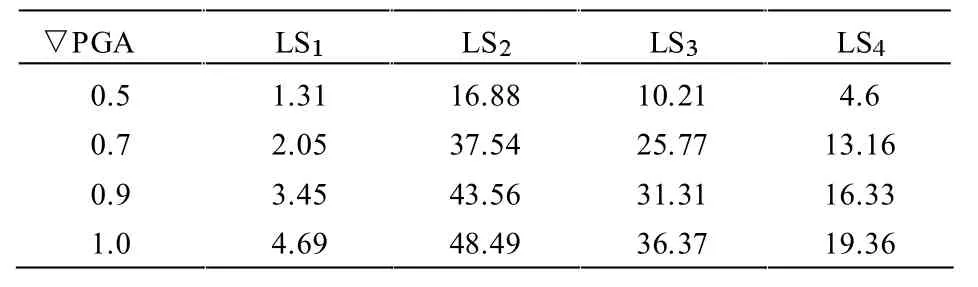
表6 不同余震幅值比下失效概率增长值 %

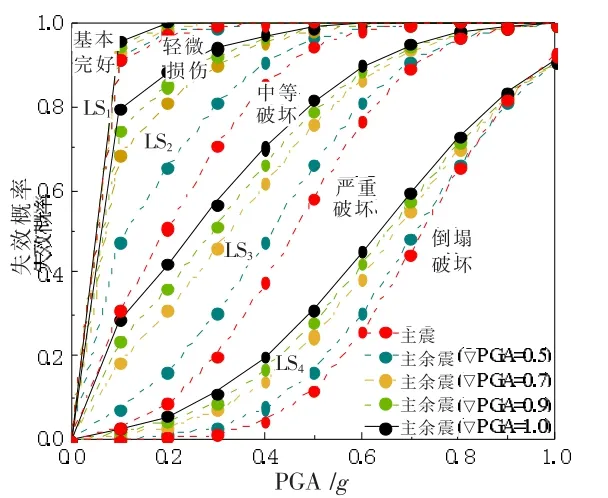
图8 不同余震幅值比下易损性曲线

由表6 可知，当余震幅值比处于0.5～1.0 时，结构发生破坏的概率较主震会提高约13.5%～42.4%（四种极限状态下中值），表明不同余震强度对结构失效概率的影响存在一定差异。

3 基于分布调幅法的易损性指数

3.1 易损性指数函数

易损性指数是用来评估结构地震损伤的一种参数[15]，主要结合结构破坏状态概率和震害指数进行计算。基于2.2 节所获得的不同余震幅值比下的易损性曲线， 采用易损性指数对不同主余震序列作用下的结构进行风险评估。求取易损性指数需先计算结构的破坏状态概率[16]P（DSj|PGA），P（DSj|PGA）可根据2.2 节图8 中各极限状态下Pf求得，见下式（4）。

式中，N 代表了极限状态的个数，j 代表了极限状态顺序，其余同上。

极限状态分布如2.2.1 节中表3 所示，对应我国的地震烈度表[17]，各破坏状态相应的震害指数如表7 所示。 基于图8 易损性曲线及式（4）求得P（DSj|PGA），计算震害指数的数学期望并用来定义结构的易损性指数(Vulnerability Index,VI)，VI 函数计算的公式式（5）所示[18]。

表7 破坏状态及相应震害指数范围及平均值

式中，DFj（j=0，1，2，3，4）为五个破坏状态相对的震害指数。 采用DFj,L、DFj,U和DFj,M代表DFj的下限值、上限值和平均值。

3.2 基于不同余震幅值比的破坏状态概率曲线

根据图8 及式（5）获得不同余震幅值比的破坏状态概率曲线，如图9 所示。

图9 基于不同余震幅值比下的破坏状态概率曲线

由图9 可知，不同余震幅值比下的破坏状态概率曲线如下所示：（1）破坏状态为DS1、DS2时，主余震的破坏状态概率均高于主震；（2）破坏状态为DS3时，主余震的破坏状态概率在0.3g 后高于主震；（3）破坏状态为DS4时，主余震的破坏状态概率在0.5g 后高于主震；（4)破坏状态为DS5时，主余震的破坏状态概率在0.9g 后高于主震。

出现主震的破坏概率高于主余震的情况的主要原因如下：以图9（a）中DS3为例说明，当PGA 小于0.3g时，主震的破坏状态概率高于主余震，表明主震作用下结构基本发生中等破坏，而同等条件主余震作用下，结构可能已经发生严重破坏，不属于中等破坏范围，所以才会出现在某些地震动强度前，主震在某一破坏状态的破坏状态概率高于主余震的情况。

由图9 还可知，结构的破坏状态概率曲线存在下降段，表明不同余震强度的破坏状态概率曲线一直处于变化中。

3.3 基于不同余震幅值比的易损性指数曲线

将3.2 节中破坏状态概率曲线、表7 中震害指数范围与式（6）结合，计算得出不同余震幅值比下结构的易损性指数，包括震害指数上下限值、平均值（VLL、VLU、VLM），获得不同余震幅值比的地震易损性指数曲线[19]。 根据易损性指数曲线，可评价不同地震强下结构的损伤程度，不同余震幅值比的地震易损性指数曲线如图10 所示。

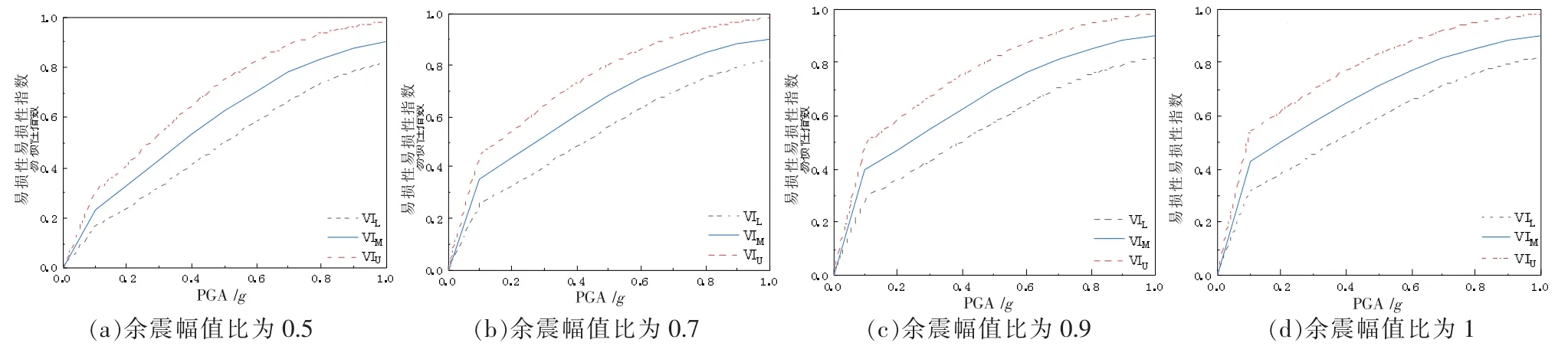
图10 不同余震幅值比下的易损性指数曲线

结合图10，获得不同余震幅值比下结构在多遇地震、设防地震和罕遇地震下的易损性指数区间，如表8所列。 研究不同余震幅值比下各地震类型易损性指数趋势，由表8 可知，结构易损性指数会随着主震强度的提高而增大；在主震强度相同时，易损性指数也会随着余震强度的提高而增大。 以多遇地震为例，发现主震的易损性指数为15.6，而余震幅值比为0.7 时，主余震易损性指数为35.6 超过了轻微破坏限值，跃迁为中等破坏状态。 表明主震在定义破坏状态中虽然起到主导作用，但是余震强度的变化有可能会造成结构破坏状态的跃迁。

表8 不同余震幅值比下易损性指数区间 %

4 结论

（1）主震幅值相同时，余震幅值比越高，结构在各极限状态下失效概率越大，表明余震幅值比越高（余震强度越强），对结构造成的附加损伤越严重；相较于相同余震强度，考虑不同余震强度下结构的失效概率使得主余震易损性曲线结果更为详细。

（2）随着主震强度的提高，相同余震强度下主余震易损性指数会大幅度增长，而在相同主震强度下，结构易损性指数会随着余震幅值比的增加而逐步增大。 表明主震在定义结构破坏状态中虽然起到主导作用，但是余震强度的变化有可能会造成结构破坏状态的跃迁。

（3）从易损性曲线以及易损性指数两个角度进行结构易损性分析可以使评估余震对结构作用时更加全面完整。 根据上述两个结论发现，该两个角度均说明进行钢框架结构设计时，仅考虑主震或单一余震强度是偏于不安全的，应考虑主震及相应不同余震强度。