Optimization of the grain boundary diffusion process by doping gallium and zirconium in Nd-Fe-B sintered magnets

Zhiteng Li(李之藤), Haibo Xu(徐海波), Feng Liu(刘峰), Rongshun Lai(赖荣舜), Renjie Wu(武仁杰),Zhibin Li(李志彬), Yangyang Zhang(张洋洋), and Qiang Ma(马强),†

1School of Rare Earths,University of Science and Technology of China,Hefei 230026,China

2Ganjiang Innovation Academy,Chinese Academy of Sciences,Ganzhou 341000,China

3Baotou Yunsheng Strong Magnet Material Co.,LTD,Baotou 014000,China

Keywords: Nd-Fe-B sintered magnet,ZrB2 phase,grain boundary diffusion,micromagnetic simulation

1.Introduction

The Nd-Fe-B alloy has been the most excellent magnet since it was invented by Sagawaet al.[1]In recent years,the rapid development of electric vehicles[2]has brought large demand for Nd-Fe-B magnets with high coercivity.Therefore,coercivity enhancement is a focus of Nd-Fe-B research.Substitution of heavy rare earth (HRE) elements, such as Tb/Dy, for Nd is a conventional strategy that is used to enhance the coercivity of Nd-Fe-B magnets, because of the higher anisotropy field (HA) of (Tb/Dy)2Fe14B than that of Nd2Fe14B.[3,4]However,the magnetic moments of the Tb/Dy and Fe atoms are antiparallel,[4,5]which causes a significant decrease in remanence(Br).

In 2000,Parket al.[6]deposited Dy film on a sintered Nd-Fe-B magnet followed by heat treatment, which is the genesis of the grain boundary diffusion (GBD) process.During the GBD process, Tb/Dy atoms diffuse from the surface into the magnet through GB phases, and a core-shell structure is formed.[7,8]The coercivity mechanism of sintered Nd-Fe-B is generally considered as a nucleation mechanism,[9]and the defects and corners of the grains make it easy for the demagnetization domain to nucleate.[10]The higherHAof the shell can inhibit the nucleation at the grain surface and the thicker GB phase layers formed by GBD also contribute greatly to coercivity.[11,12]Compared with the addition of Tb/Dy,the decrease in remanence is much smaller.

However, the coercivity increment by GBD tends to decrease when the magnet thickness increases.[13]Therefore,researchers have put considerable effort into increasing the depth of diffusion.At present,a lot of research is concerned with the development of diffusion sources, which can be divided into three types,[14]including HRE-based,[15-17]light rare-earthbased[18-21]and non rare earth based[22-24]diffusion sources.In addition to the diffusion sources, studies showed that the compositions in magnets have important effects on GBD.Baeet al.[25]reported that oxygen has a negative effect on GBD.A lower Al content in the magnet was found to be beneficial to GBD by Diaoet al.[26]And Zhonget al.[27]found that the Ti element in the Nd-Fe-B has a positive effect on GBD.However, research on the influence of the magnet on GBD is still insufficient.To gain a comprehensive understanding of GBD,it is necessary to determine how the magnet itself influences GBD.

Ga and Zr are commonly used doping elements in Nd-Fe-B,which have been well studied.[28,29]Ga doping can improve the wettability of the Nd-rich phase to form a continuous GB layer,[9,30,31]and Zr doping can refine the grains by pinning in GB phases.[32]The main purpose of Ga and Zr doping is to optimize the GB phases and microstructure of magnets,and Xuet al.[33]reported that GB phases play an important role in GBD.Ga and Zr doping may have some effects on GBD,but they are still unknown.To optimize GBD,a comprehensive study of the factors that may affect GBD is necessary.Therefore,it is worth studying the influence of these two doping elements on GBD.

In the field of permanent magnets, micromagnetic simulation is an effective way to study the relationship between microstructures and magnetic properties.[34-36]In this paper,micromagnetic simulation was used to further analyze the different structures of the magnet based on the experiment.

2.Experimental and simulation methods

2.1.Sample preparation and characterization

Three kinds of samples with the compositions of

were prepared via a powder metallurgical process, including strip-casting,hydrogen decrepitation and jet milling.The median particle sizes were controlled to about 3.7 µm for all samples.The fine powders were compressed and oriented under a 2.0 T magnetic field, followed by isostatic pressing at 195 MPa.Next,the green compacts were sintered(1030°C-1080°C)and annealed(900°C for 1st and 500°C-600°C for 2nd)at their respective optimal temperatures to achieve the optimum magnetic properties.These samples before GBD were marked as original,Ga-doped and Zr-doped,respectively.The magnets before GBD were cut into cylinders with a size ofφ10×6 mm.The samples were polished and then washed in distilled water ultrasonically.Next,the magnets were acidized in 3%nitric acid for 50 s.Then,the magnets were cleaned with distilled water and alcohol ultrasonically.Subsequently,all the magnets were covered by Tb film via a magnetron sputtering system.A commercial Tb target(99.9%,Hefei Kejing Materials Technology Co.,Ltd.) was used to fabricate the diffusion source.During the deposition, the argon pressure was maintained at 1 Pa,and the direct current power was set to 120 W.The film weights were controlled at 0.42 wt% of the magnet for all the samples.All three magnets were then treated at 900°C for 6 h in vacuum, and annealed at the optimal temperature(500°C)for 3 h in vacuum.Samples after GBD were marked as original GBD,Ga-doped GBD and Zr-doped GBD,respectively.

The magnetic properties of the samples were measured by a B-H tracer(NIM-500C).The microstructures of the samples were observed using a backscattered electron scanning electronic microscope (BSE-SEM) (JEOL JSM 7200F).The element distributions were obtained via electron probe micro analysis (Shimadzu EPMA-1720H).The crystal structure of micro-areas in the triangular junction phase (TJP) was characterized using transmission electron microscopy (TEM, FEI Tecnai G2 F20).

2.2.Micromagnetic simulation

The parallel finite element micromagnetic package Magpar[37]was used for micromagnetic simulation to understand the effect of Tb-rich shell thickness on coercivity.In this work,a model with a polycrystalline microstructure based on Voronoi tessellation[38]was established by Neper[39]and Gmsh.[40]This model was a cube with a size of 300 nm×300 nm×300 nm containing 27 irregular grains, as shown in Fig.1.Due to the limitation of computing capability, the grain size in this model was smaller than the actual grain size.In addition, the model consisted of three parts, namely, the core of Nd2Fe14B,the shell of(Tb0.25Nd0.75)2Fe14B,and the GB phases.All the grains were surrounded by a Tb-rich shell and separated by GB phases.The width of the GB was set to about 5nm.The influence of the shell thickness on coercivity was studied by changing the shell thickness from 0 nm to 10 nm.The material parameters of Nd2Fe14B and Tb2Fe14B were taken from the literature.[4,41]The saturation magnetic polarizations (JS) were 1.61 T and 0.7 T for Nd2Fe14B and Tb2Fe14B.The anisotropy constants(K1)were 4.5 MJ/m3and 5.9 MJ/m3for Nd2Fe14B and Tb2Fe14B.And the exchange stiffness (A) was 12.5 pJ/m and 13.3 pJ/m for Nd2Fe14B and Tb2Fe14B.The magnetic properties for the GB phases were defined as amorphous soft magnetic phases[15]andJS,K1,andAwere 0.15 T,0 MJ/m3, and 5 pJ/m, respectively.The magnetic parameters for (Tb0.25Nd0.75)2Fe14B were obtained by linear interpolation.

3.Results and discussion

3.1.Magnetic properties

Figure 2 shows the demagnetization curves and the comparison of the coercivity of the samples with different doping elements before and after GBD.The detailed magnetic properties are listed in Table 1.With Ga or Zr doping,the coercivity decreases slightly from 14.38 kOe to 13.41 kOe or 13.63 kOe,respectively.The decrease in magnetic properties may be due to the excessive addition of Ga or Zr.[42,43]The coercivities of the three GBD samples are all enhanced significantly after diffusion, but the coercivity increments of the three samples are quite different,as shown in Fig.2(b).The coercivity of the original magnet increases by only 23% through GBD,from 14.38 kOe to 17.62 kOe.The coercivity increment of the Ga-doped magnet is slightly higher, increasing by 32% from 13.41 kOe to 17.73 kOe.In contrast,the coercivity increment for the Zr-doped magnet is 7.97 kOe,increasing by 58%from 13.63 kOe to 21.60 kOe, which is quite huge for a magnet with a thickness of 6 mm.The results show that both Ga and Zr have a positive effect on GBD,but the effect of Zr is particularly significant.

The performances of the GBD samples at high temperatures were also measured,as shown in Fig.3.The temperature coefficients of remanence(α)and coercivity(β)in the range ofTtoTiare calculated by the following equations:[44]

The temperature coefficient of remanence of the Ga-doped and Zr-doped GBD magnets decreases slightly compared with the original GBD magnet, from-0.104 %/°C to-0.107 %/°C and-106%/°C,respectively.However, it can be found that the temperature coefficient of coercivity of the Zr-doped GBD magnet increases significantly to-0.530 %/°C, while it is only-0.622 %/°C and-0.630 %/°C for the original GBD magnet and Ga-doped GBD magnet.The results show that the demagnetization resistance of the Zr-doped GBD magnet at high temperature is greatly improved compared with the other two samples,which can be used in high-temperature applications.

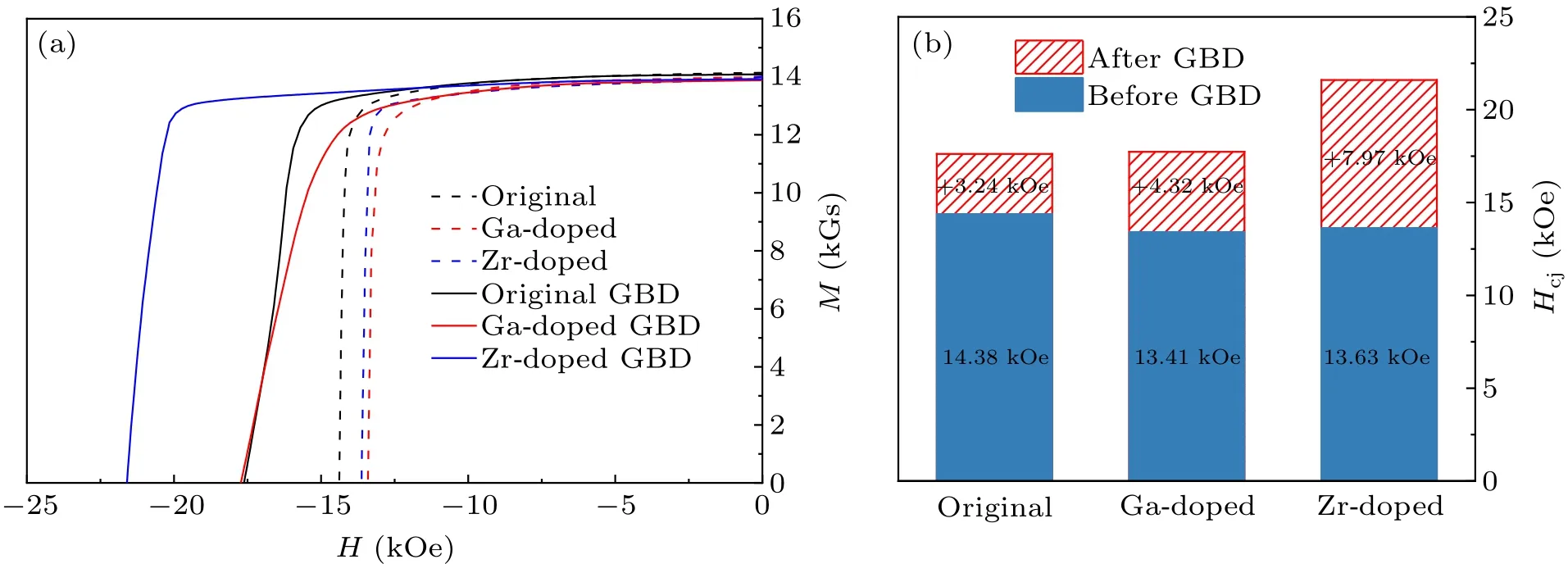
Fig.2.(a)Demagnetization curves and(b)the coercivity comparison of the original,Ga-doped and Zr-doped magnets before and after GBD at room temperature.

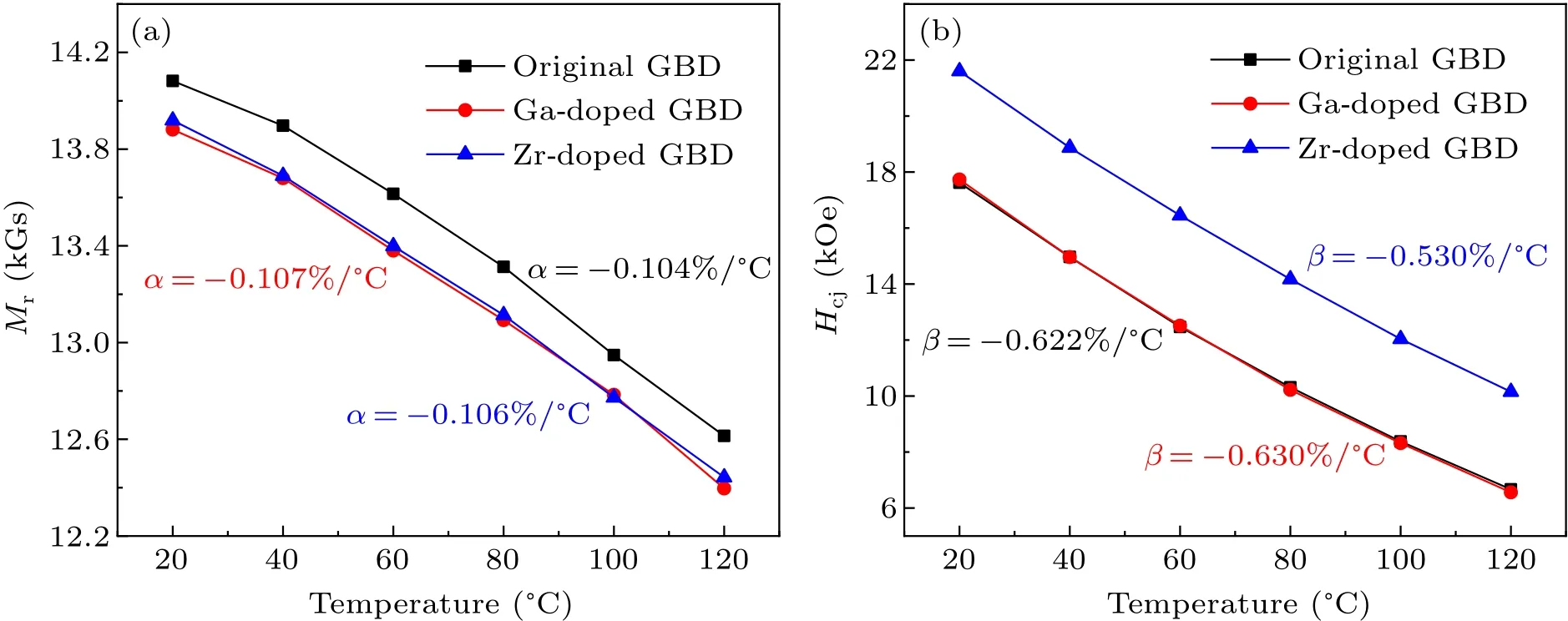
Fig.3.The temperature dependence of remanence (a) and coercivity (b) of the original GBD magnet, Ga-doped GBD magnet and Zr-doped GBD magnet.

3.2.Microstructure characterization and analysis

The literature indicates that the coercivity increment by GBD is derived from the Tb-rich shell and the optimization of GB phases.[12]It implies that the Ga or Zr doping may have influences on the optimization of the Tb-rich shell structure or GB phase.Therefore,the microstructure evolution of magnets doped with different elements before and after GBD was analyzed to explore the reason for the differences in the coercivity increments.Figure 4 shows the BSE-SEM images of three samples before and after GBD.There are three different contrast areas, white, dark gray and light gray, which respectively represent the GB phases, (Pr, Nd)2Fe14B main phases,and (Tb, Pr, Nd)2Fe14B shells.It can be found in Fig.4(i)that there are some regions with different contrasts in the TJP(circled in red),which may be a new phase due to the addition of Zr.Figures 4(b), 4(f), and 4(j) display the morphologies of the corresponding three magnets after GBD at the depth of 20µm,respectively.Core-shell structures can be observed in all three magnets.For all three magnets after GBD, the shell thickness decreases with the increase in diffusion depth.It is also hard to observe the clearly visible shells in the original GBD and Ga-doped GBD magnets(Figs.4(c)and 4(g))at the depth of 100 µm.However, it is very interesting that there are still many thin shells in the Zr-doped GBD magnet at a depth of 100µm, and the shells were more uniform.Even at a depth of 200µm,there are still thin shells on the surface of some grains,as shown in Fig.4(l).In contrast,Tb-rich shells almost completely disappear and the GB phase is discontinuous in the original GBD and Ga-doped GBD magnets at the depth of 200µm.This means that there is more uniform distribution in the depth of Tb in the Zr-doped GBD magnet.It is worth noting that the shell thickness on the surface of the magnet decreases with the increase in the diffusion depth, as shown in Figs.4(b),4(f),and 4(j).The shells around the main phase in Figs.4(b)and 4(f)are much thicker with 2µm.But the shell thickness in Fig.4(j) is only about 0.7 µm.Therefore,the difference in the coercivity increment by GBD of the three magnets can mainly be attributed to the distribution of Tb atoms.

Fig.4.BSE-SEM images of the original magnet(a),the Ga-doped magnet(e),the Zr-doped magnet(i)and original GBD magnet(b)-(d),the Ga-doped GBD magnet(f)-(h),and the Zr-doped GBD magnet(j)-(l)at depths of 20µm,100µm,and 200µm.

To more accurately describe the Tb distribution of the three magnets after GBD,EPMA characterization was carried out, as shown in Fig.5.The results show that Tb atoms are enriched on the surface of the magnet.With the increase in depth,the proportion of the Tb-rich area and the concentration of Tb drop significantly.According to Fick’s law,the concentration gradient is the main driving force for diffusion.Therefore, the decrease in the Tb concentration gradient with the increase in depth is the main reason.When the depth exceeds 100µm,Tb elements are difficult to detect in the original GBD magnet.In contrast,Tb elements can still be observed in relatively low concentrations at the depth from 100µm to 200µm in the Ga-doped GBD magnet, but the green relatively lowconcentration Tb area basically disappears when the diffusion depth exceeds 200 µm, as shown in Fig.5(b).In particular,in Zr-doped GBD magnets, when the depth exceeds 200µm,the distribution of the green relatively low-concentration Tb area can still be detected,as shown in Fig.5(c).Moreover,the uniformity of the Tb distribution in the Zr-doped GBD magnet is significantly improved.Both the diffusion depth and distribution uniformity of the Tb elements are consistent with the increment of coercivity for GBD magnets.Accordingly, the Tb element distribution and diffusion depth shown by EPMA agree with the results of BSE-SEM.

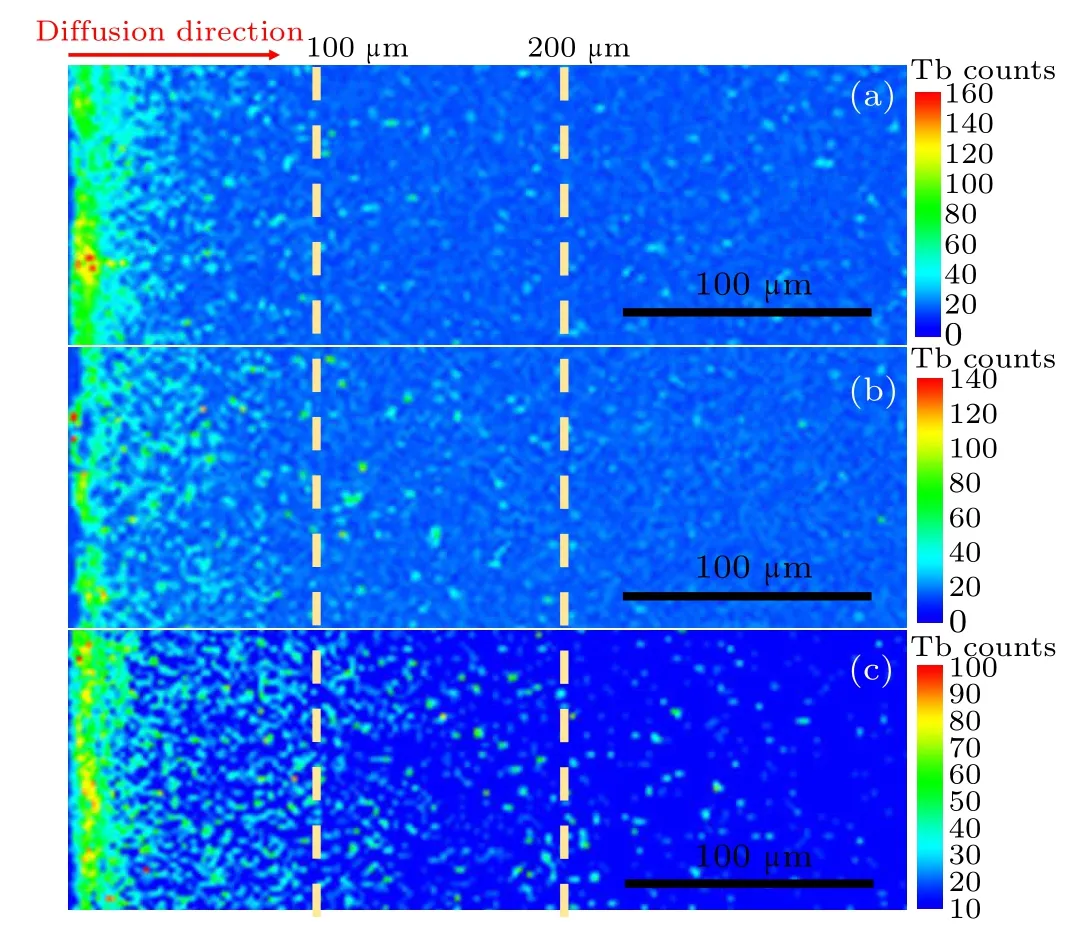
Fig.5.EPMA mappings of Tb in the original magnet(a),the Ga-doped magnet(b)and the Zr-doped magnet(c)after GBD at the depth of 0µm to 300µm.

Figures 6(b),6(d),and 6(g)shows the high-magnification EPMA mappings of the Tb distribution of three GBD magnets at the depth of 100µm.The mapping shows that Tb is mainly distributed along the GB phase and exhibits a dispersion distribution.It is difficult to distinguish the core-shell structure in the original GBD magnet.In addition,the Ga-doped GBD magnet exhibits a discontinuous Tb-rich network.In contrast,the Tb-rich shells of the Zr-doped GBD magnet are complete and continuous.Similar results can be observed in the corresponding SEM in Figs.6(a), 6(c), and 6(f).Specifically, the concentration and distribution uniformity of Tb in the original GBD magnet,Ga-doped GBD magnet and Zr-doped GBD magnet at the depth of 100 µm are significantly improved in turn.This indicates that Zr doping can effectively optimize the distribution of Tb.The nucleation field of the reversed domain on grain surfaces is enhanced when it is covered by shell,and a complete shell can reduce the nucleation sites.[11]

To understand how the doping elements Ga and Zr affect diffusion depth,the distributions of Ga and Zr were also analyzed via EPMA,as shown in Figs.6(e)and 6(h).It is found that Ga atoms are distributed in the TJP,as shown in Fig.6(e).The melting point of Ga is low, which can lower the melting point and improve the fluidity of GB phases.GB phases are the channels for GBD, and the decrease in the melting point of the GB can facilitate the migration of Tb atoms.Similar to the distribution of Ga,Zr also exists in the TJP in the Zr-doped GBD magnet,as shown in Fig.6(h).Figure 6(i)shows that the B elements are also enriched in the Zr-rich region, indicating the formation of the Zr-B compound, which corresponds to the phase with different contrast in Fig.4(i)mentioned above.

Fig.6.SEM images[(a), (b), (c)]and EPMA mappings of Tb[(b), (d), (g)], Ga(e), Zr(h), and B(i)of the original GBD magnet, the Ga-doped GBD magnet and the Zr-doped GBD magnet at the depth of 100µm.

The Zr-B compound in the TJP may be the main reason for the different distribution of Tb.To further analyze the role of Zr-B compounds in the TJP,TEM analysis was performed.Figure 7(a)shows the TJP that contains the Zr-B phase.The Zr-B phase has a strip morphology and is completely encapsulated inside the TJP.According to Fig.7(b),the selected area electron diffraction(SAED)of the Zr-rich area shows that this area in the TJP is consistent with the structural characteristics of hexagonal ZrB2,whose melting point is about 3000°C.Because the formation of ZrB2consumes boron,the consumption of boron leads to the reduction of Nd2Fe14B,[29]thus more GB phases are formed.The distribution of GB phases observed in Figs.4 and 6 also verifies this result.Therefore, the formation of ZrB2can provide a continuous GB structure for GBD.Moreover,we find that ZrB2is completely encased in the TJP.There are also many lattice dislocations between the TJP and ZrB2phase,as shown in Fig.7(c),resulting in a high concentration of defects at the interface,[27]which have a high Gibbs free energy.Therefore,Tb atoms need less diffusion activation energy at defect sites,which accelerates atomic diffusion.

3.3.Micromagnetic simulation results

Zr doping can significantly increase the diffusion depth,while the shell thickness near the surface also decreases, as shown in Fig.4.To find out whether the reduction in shell thickness would have a negative effect on coercivity, we carried out a micromagnetic simulation.Figure 8 shows that the coercivity is in accordance with the thickness of the shell.However, the effect of shell thickness on coercivity becomes small when the thickness exceeds 5 nm.In the range of 0 nm to 5 nm,the coercivity increases by 1975 Oe/nm,but by only 425 Oe/nm in the range of 5 nm to 10 nm.According to the simulation results, thin shells are enough to provide a large coercivity increase.The decrease in shell thickness within a certain range does not have a significant negative effect on coercivity.Therefore, the distribution of Tb in the Zr-doped GBD magnet is more advantageous to obtain higher coercivity, i.e., more Tb elements diffusing into the interior of the magnet to form thin shells.With the same amount of the Tb diffusion source(0.42%in this work),the thin shell also means that there can be more Tb surplus to provide the concentration gradient of Tb diffusion to the deeper part of the magnet.

Fig.8.(a) Demagnetization curves and (b) the coercivity increment for models with shell thicknesses of 0 nm,2.5 nm,5 nm,7.5 nm,and 10 nm,calculated by Magpar.

Fig.9.Magnetization reversal patterns on the outer surfaces(a)and crosssections of x=0.9(b)and z=0.93(c)of models with shell thicknesses of 0 nm,5 nm,and 10 nm.

Moreover,the magnetization reversal patterns are shown in Fig.9.A clear difference can be observed between the magnets before and after GBD.In the model without Tb-rich shells, the magnetic moment begins to reverse at the GB and the edges of the grain surface (blue contrast).In the models with shells,the reversed domains move from the edges of the grain surface to the edge of the core not covered by the Tb-rich shells.The magnetization reversal patterns are also similar for the models with 5 nm shells and 10 nm shells,except that the nucleation site moves further into the grain in the model with 10 nm shells.Due to the influence of the demagnetizing field,the nucleation field at the grain surface is low.After GBD,the grain surface is covered by Tb-rich shell, which significantly improves the nucleation field at the grain surface.With a further increase in the shell thickness, the nucleation site moves further into the grain.However,from the surface of the magnet to the interior,the demagnetizing field gradually decreases and the distribution of this field inside the magnet is more uniform.[45]Thus,the nucleation field does not increase much when the nucleation site moves into the grain, which can explain why the coercivity increases little as the shell thickness increases further.Therefore, a 5 nm thin shell is enough to achieve high coercivity.Also,the thicker Tb-shells on the surfaces of the original GBD and Ga-doped GBD magnets result in a waste of Tb.

4.Conclusion

In summary, we found that Ga doping can decrease the melting point and facilitate the fluidity of GB phases,making it easier to form continuous GB phases.Therefore,Ga doping in magnets can slightly improve the coercivity increment by GBD, from 3.24 kOe to 4.32 kOe.The consumption of B in the Zr-doped magnet leads to an increase in the GB phases,which can promote the formation of continuous GB phases.More important is the increase in the defect concentration between ZrB2phases and GB phases in the TJP, causing high Gibbs free energy in the TJP, which makes the Tb atoms require less diffusion activation energy during migration.Therefore,Zr doping improves the diffusion depth and uniformity of Tb,which is the direct reason that allows Zr-doped magnets to achieve a 7.97 kOe increment by GBD technology.In the Zrdoped magnet, the increase in diffusion depth will lead to a decrease in shell thickness near the surface.In addition, the reduction in shell thickness within a certain range was found not to have a significant negative effect on coercivity by micromagnetic simulation.This study helps to understand the role of Ga and Zr in the GBD process,and may provide a new perspective for researchers to improve the effects of GBD.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant No.52261037),self-deployed Projects of Ganjiang Innovation Academy, Chinese Academy of Sciences(Grant No.E055B002),the Project of Baotou City Science and Technology(Grant No.XM2022BT04),the Key Research Program of the Chinese Academy of Sciences (Grant No.ZDRW-CN-2021-3) and the Key Research Project of Jiangxi Province(Grant No.20203ABC28W006).

The authors would like to thank Professor Zhenchen Zhong,Jiangxi University of Science and Technology,for providing guidance for this work.