Single-qubit quantum classifier based on gradient-free optimization algorithm

Anqi Zhang(张安琪), Kelun Wang(王可伦), Yihua Wu(吴逸华), and Sheng-Mei Zhao(赵生妹),2,†

1Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Ministry of Education,Nanjing 210003,China

Keywords: single-qubit quantum classifier, gradient-free, parameters optimizing, barren plateau, quantum noise

1.Introduction

Classification has been one of the main issues in quantum computing.[1-6]There are several types of quantum classifiers.some are inspired by their classical counterparts with their kernel parts replaced by a high-depth quantum circuit,[7,8]and some are inspired by the neural networks with multi-layer quantum circuit structures.[9-13]These quantum classifiers always require expensive subroutines.Others are termed quantum circuit learning with a hybrid quantum-classical (HQC)structure[14-21]and train a shallow-depth parameterized quantum circuit with a classical optimizer.

By using a small amount of quantum resources,quantum classifiers based on an HQC structure have become a promising candidate in the noisy intermediate scale quantum(NISQ)era.For example,Ref.[19]built a model with only two qubits in the quantum circuit that could simultaneously manipulate two classes of training samples, which reduced the training processing time by half.Furthermore,Ref.[20]trained multiclass data, more than 2 classes, simultaneously for classification tasks in the qubit system.Reference [21] presented single-qubit processing units which can be seen as a singlequbit quantum classifier (SQC) and the quantum circuit was organized as a series of data re-uploads, in which a multiple data re-uploading method is used to increase circuit express ability.The advantage of SQCs is that they avoid the connectivity constraints and embedding problems of qubits in quantum devices.But the SQC still has a difficulty that needs to be solved when using the quantum-classical hybrid scheme to implement it.

The gradient-based parameter optimization method inside a quantum classifier,such as the Adam optimizer,may lead to the barren plateau[22](i.e.,vanishing gradient)problem.There are some solutions to overcome this issue.For instance,a layer wise learning optimization method was proposed by Skoliket al.[23]to update only a subset of the parameters in each training iteration.A Bayesian optimization (BO) based on Gaussian process regression (GPR) and noisy expected improvement (NEI) was proposed by Iannelliet al.[24]to provide a more precise estimation of the ground state energy in a few iterations.An efficient method for simultaneously optimizing both the structure and the parameter values of quantum circuits was proposed by Ostaszewskiet al.[25]It has been demonstrated that the quantum convolutional neural networks (QCNNs)proposed by Pesahet al.[26]don’t show barren plateaus for the variance of the gradient vanishes no faster than polynomially.However,whether a single-qubit quantum classifier yields higher accuracy in solving classification tasks has not been discussed yet.

In this work, we propose a gradient-free optimization(GFO)algorithm based single-qubit quantum classifier(SQC),named the GFO-based SQC.In the GFO algorithm,a rotation gateRX(φ) applied on one qubit initialized as|0〉 can be regarded as a binary quantum classifier.Training data and parameters of the quantum classifier are loaded intoφwith the form of vector-multiplication.The cost function is decreased by finding the value of each parameter that yields the minimum expectation value of measuring the quantum circuit until it meets the stop condition.After several iterations, the cost function is converged and the optimal parameters are obtained.The classification information for unclassified data can be determined by the result with the highest probability after measuring the quantum circuit of the SQC.

The advantages of the proposed GFO-based SQC are three-fold.1) Compared with the gradient-based algorithm,the GFO algorithm requires less time for optimizing the parameters.2) Parameters are loaded as weights of each component of the training data in the GFO-based SQC,which can save more qubits and quantum gate resources and further reduce the barren plateau problem.3)The updated value of the parameter is calculated with the usage of the statistical average method,thus increasing the accuracy of classification.

2.The single-qubit quantum classifier based on the gradient-free optimization algorithm

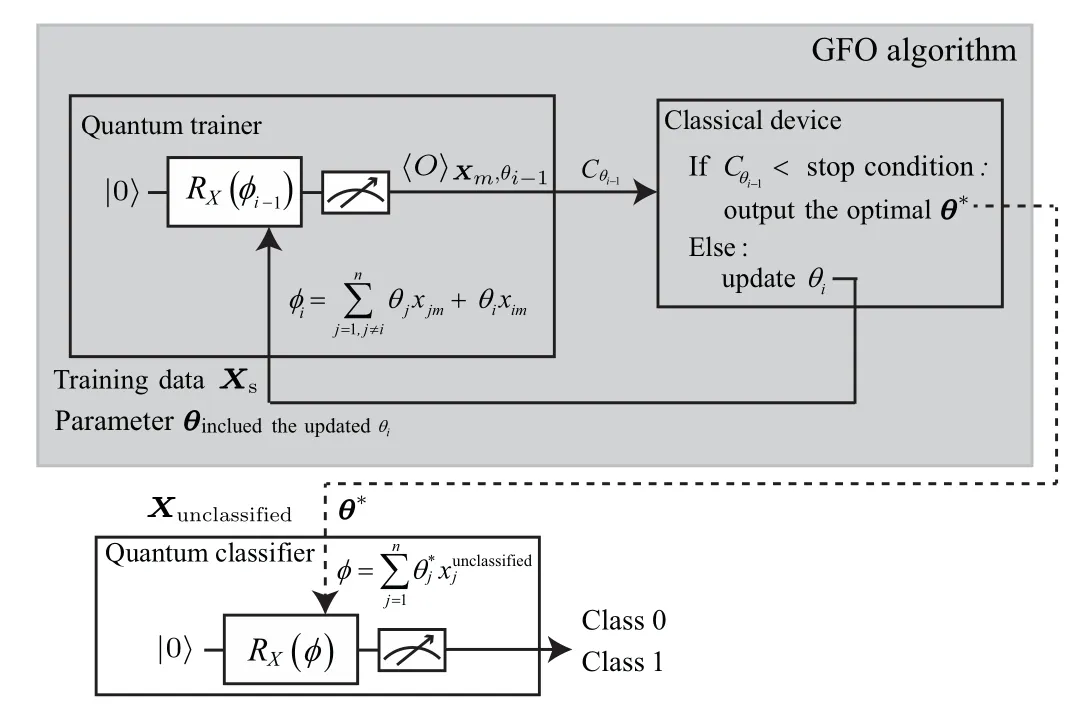
Fig.1.The framework for optimizing parameters of the SQC based on the GFO algorithm.The arrows in the figure represent the flow of information.In the training processes(gray box),the training data X and the parameters θ are fed into φ of the rotation gate in the form of vector-multiplication every iteration.The value of the cost function Cθi-1 is obtained by measuring the quantum circuit with the(i-1)-th parameters and checking whether it’s less than the given stop condition.If not,continue the next parameter-optimizing iteration where other parameters are fixed except θi,which is updated in the i-th iteration; otherwise,begin the testing processes,where the optimal parameters vector θ∗and unclassified data Xunclassified are fed into the same circuit.The classification information of Xunclassified can be specified with the highest probability by measurement of the quantum circuit.

Here,we detail the findings of the optimal parameter vectorθ∗.Inspired by the optimization strategies in Ref.[25],we consider a special case where a subset only contains one parameter to optimize in the parameterized quantum gate for the quantum circuit.Firstly,the expectation value of the quantum circuit with structureUand initial stateρcan be rewritten as a function of angleφ[25]which has sinusoidal form as〈O〉φ=Tr(OUρU†)=Asin(φ+B)+C,whereA,BandCare coefficients that need to be determined.Then,we consider the task of minimizing the value of the cost functionCθiby maximizing every|〈O〉Xm,θi| part with thei-th parameter, which can be ensured if the coefficients are estimated.Therefore,using the definition of the matrix exponential,the expectation value can be expressed as

From the identity deformation of the sinusoidal function,we can obtain a compact expression of Eq.(2)as

where

where arctan2(A,B) is a four quadrant arctangent of the real numbersAandB,and its value range is(-π,π].It’s easy to locate the maximum atθimxim=π/2-arctan2(A,B).Therefore,the updated value of thei-th parameterθimcan be expressed as

Thei-th parameter can be optimized by a batch of training data,where a strategy to obtain the average value ofm i-th updated parameters in each iteration is

whereMis the number of training data in a batch.The algorithm finds each updated parameter inθsequentially for alli=1,...,nto complete cycle by cycle until a stop condition is satisfied.The gradient-free method is Algorithm 1.

Algorithm 1 Gradient-free optimization algorithm for the SQC Require: Initialize the parameters θi randomly,where 1 ≤i ≤n;set batch size M (we set M as 10 in this work);a stop condition;estimate〈O〉0,〈O〉π,〈O〉π 2,〈O〉-π 2;1: loop 2: Calculate the value of the cost function as cost-now.3: for i=1 to n do 4: For all parameters except the i-th one.5: for m=1 to M do 6: Calculate θ＇mX＇m;A= 1 2)sin(θ＇mX＇m)];B= 1 2[(〈O〉0-〈O〉π)cos(θ＇mX＇m)+(〈O〉π 2 -〈O〉-π 2)cos(θ＇mX＇m)+(〈O〉0-〈O〉π)sin(θ＇mX＇m)];θopt im ← 1 2[(〈O〉π 2 -〈O〉-π Xim(π2 -arctan2(A,B)).7: end for M ∑Mm=1 θopt im.Calculate cost value: cost-new.8: if cost-new ＜cost-now then Get the average: θopt i = 1 9: θopt i changed;cost-now=cost-new.10: else 11: θopt i remains the same.12: end if 13: end for if the condition is met.14: end loop

3.Results and discussion

In this section,we demonstrate the feasibility of the proposed GFO-based SQC with the Iris and MNIST datasets.We use the PennyLane[27]module in Python to realize the proposed algorithm.In order to show the performance of the proposed GFO-based SQC,the Adam-based SQC is simulated at the same time, whose parameters are optimized in a hybrid quantum-classical way.In addition,the quantum support vector machine(QSVM),which is a quantum classifier without a classical part,is also selected for comparison.

For the Iris dataset, we use 40 training samples and 10 testing samples for each class,and they are selected randomly from the Iris dataset.Here, the optimizing parameters’ time is recorded when 100%classification accuracy is achieved using the GFO-based SQC,Adam-based SQC,and QSVM.The simulations are performed 20 times, where the quantum circuit has no noise.As shown in Fig.2, the time using the GFO-based SQC is on average smaller than that using the Adam-based SQC, except the third, the ninth, and the eighteenth times, which means that the proposed GFO algorithm not only has a higher efficiency for classification,but also has a reduced time for the parameters’ optimization.Here, the time using the GFO-based SQC fluctuates because the training effect of the GFO-based SQC is highly dependent on the original parameters when the dataset is relatively simple.The time cost of using the QSVM is much higher than that of using both the GFO-based SQC and the Adam-based SQC,because the QSVM requires a lot of time for the kernel calculations.Therefore, we only compare the proposed GFO-based SQC with the Adam-based SQC in the MNIST dataset.

Fig.2.The time when 100% classification accuracy is achieved using the GFO-based SQC (red), Adam-based SQC (blue), and QSVM(green)for the Iris dataset versus the simulation times.

For the MNIST dataset, we use 10000 training samples and 1000 testing samples for each class, which are selected randomly from the MNIST dataset.Each sample is processed into 32 dimensions by the rough grid feature method.[28]The simulations are performed 20 times separately based on the quantum circuit with and without noise deriving from the imperfections of quantum gates.Here, the quantum gate is affected by the five typical types of quantum noise,i.e.,bit flip,depolarizing,phase flip,phase damping,and amplitude damping.Here, the error probability for the five quantum noises is assumed to be 5%.The parameters of the quantum circuit have been updated for 15 loops in each simulation.

Firstly,we compare the optimizing time and classification accuracy by using the GFO-based SQC and the Adam-based SQC for different classification tasks in the MNIST dataset.As shown in Table 1, the GFO-based SQC can complete the classification tasks for both the digits that are similarly written by hand(such as 1,7)and those that are difficult to recognize when written(such as 2,4,6,8 and 9),and takes less time than the Adam-based SQC over 15 loops.

Table 1.The optimizing time and classification accuracy using the GFObased SQC and the Adam-based SQC for different classification tasks in the MNIST dataset.

Next,we compare the time of optimizing the parameters of the two SQCs in different environments for the classification task between 0 and 1.According to Ref.[29],phase flip and phase damping have different Kraus matrices,but by simply substituting, one can check directly that the two channels yield completely the same outputs,which means that the phase flip quantum operation is exactly the same as the phase damping.Therefore, we only present the results under phase flip noise.As shown in Table 2, the optimizing time required by the GFO-based SQC is less than that of the Adam-based SQC in both no-noise and noisy environments.Furthermore, the optimizing time of the GFO-based SQC is basically stable at 1500 s, while the Adam-based SQC is heavily influenced by the environment.

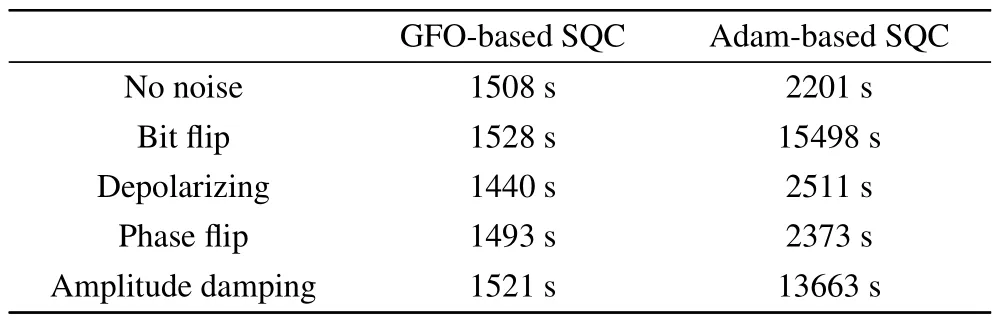
Table 2.The average optimizing time using the GFO-based SQC and the Adam-based SQC in different environments for the MNIST dataset.

Finally,we demonstrate the details of the two-class classification task between 0 and 1 with and without quantum gate noise.The shadow is composed of 20 simulations with different initial parameters.

Figure 3 shows the value of cost(a)and the classification accuracy(b)against time for the two-class classification task.As shown in Fig.3(a), the convergence ability of the GFObased SQC is better than that of the Adam-based SQC with different initial parameters.As shown in Fig.3(b), the GFObased SQC can achieve a high classification accuracy faster than the Adam-based SQC and can be stable at a specific accuracy in the end.

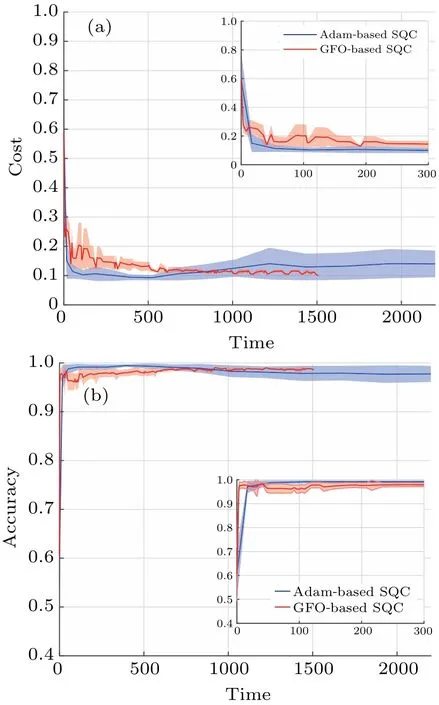
Fig.3.Quantum gate without noise,(a)for the value of the cost function and(b)for the accuracy of classification.

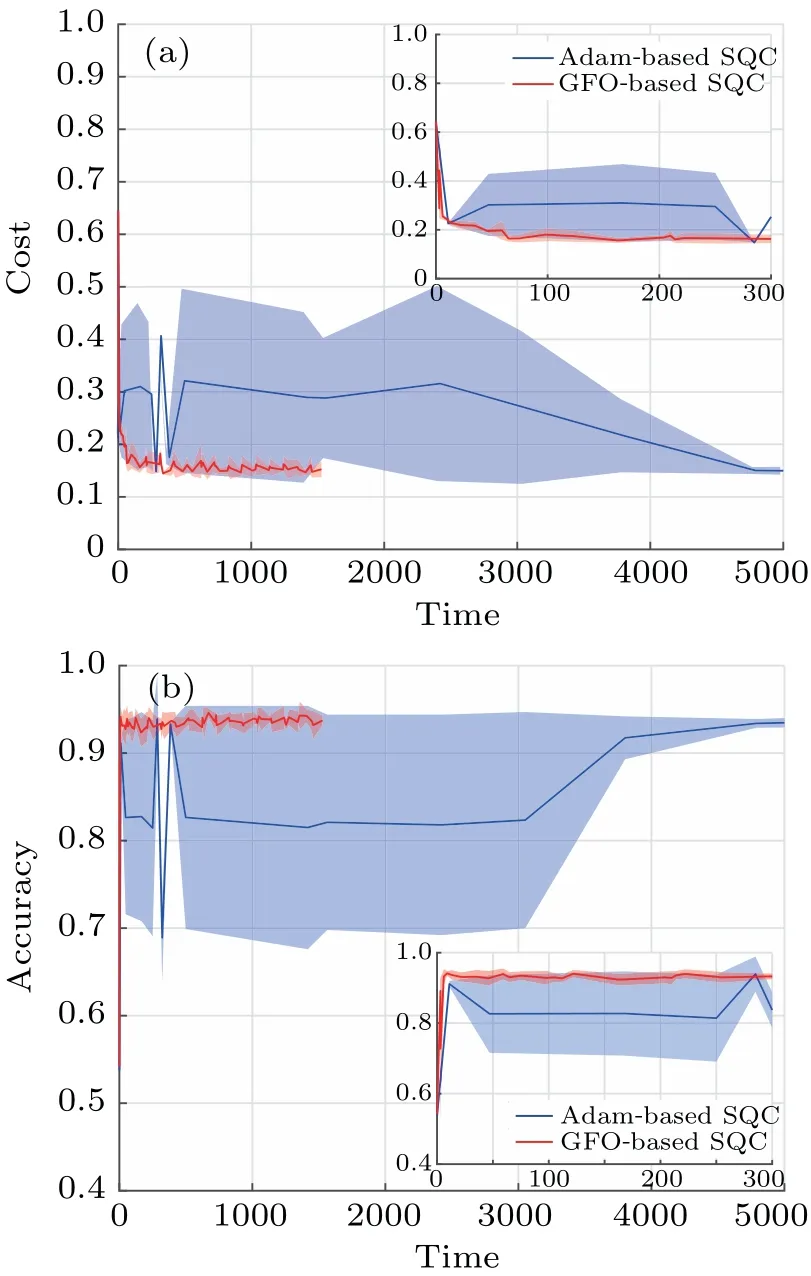
Fig.4.Quantum gate with bit flip noise, (a) for the value of the cost function and(b)for the accuracy of classification.

Figure 4 shows the situation of bit flip noise affecting the quantum gate where(a)shows the value of cost and(b)shows the classification accuracy against time.The shaded area of the Adam-based SQC is larger than that of the GFO-based SQC, indicating that the GFO-based SQC is effective and is more adaptable in the noisy environment of bit flip and takes less time to finish 15 loops of optimizing parameters.From Fig.4(a),the GFO-based SQC has a more stable convergence ability than the Adam-based SQC.From Fig.4(b), the GFObased SQC is able to reach a high accuracy faster than the Adam-based SQC.

Figure 5 shows the situation of depolarizing noise affecting the quantum gate.Figure 5(a)shows that the convergence ability of the GFO-based SQC is better than that of the Adambased SQC,indicating that the GFO-based SQC is effective in the depolarizing noise environment and takes less time to finish 15 loops of optimizing parameters.Figure 5(b)shows the GFO-based SQC is able to reach a high accuracy faster than the Adam-based SQC and can be stable at a specific accuracy in the later stages.

Fig.5.Quantum gate with depolarizing noise, (a) for the value of the cost function and(b)for the accuracy of classification.

Figure 6 shows the situation of phase flip noise affecting the quantum gate.Figure 6(a)shows that the GFO-based SQC has the ability to resist the phase flip noise and keep stable continuous convergence, while the Adam-based SQC fluctuates badly.Figure 6(b) shows that the GFO-based SQC can achieve a high classification accuracy faster and can be stable at a specific accuracy in the later stages.The results in Fig.6 show that the GFO-based SQC is effective in the noisy environment of phase flip.

Fig.6.Quantum gate with phase flip noise,(a)for the value of the cost function and(b)for the accuracy of classification.

Fig.7.Quantum gate with amplitude damping noise, (a)for the value of the cost function and(b)for the accuracy of classification.

Figure 7 shows the situation of amplitude damping noise affecting the quantum gate.As is shown in Fig.7(a), the GFO-based SQC takes less time to finish 15 loops of optimizing parameters but the Adam-based SQC has a better convergence ability.Figure 7(b)shows that the GFO-based SQC can achieve a high classification accuracy faster, but the Adambased SQC can reach a higher accuracy eventually.

In general, the GFO-based SQC has a certain resistance to noises and can keep the ability of continuous convergence.Compared with the Adam-based SQC, the GFO-based SQC can finish 15 loops of optimizing parameters more quickly.Although the GFO-based SQC is affected by the randomly initialized parameters, which makes the optimization performance of the GFO-based SQC fluctuate in the optimizing processes,the GFO-based SQC can always achieve a high classification accuracy faster than the Adam-based SQC and maintain stability in the end.As gradients do not need to be calculated,the GFO-based SQC saves lots of calculation time and can quickly complete the optimizing processes, while the Adambased SQC is affected badly by the different noises and takes different times to finish the optimizing processes in different noise environments.

4.Conclusion

In this work, we have proposed a GFO-based SQC.By loading training data and parameters in a summation form,only one rotation gate has been used in the quantum circuit.The proposed GFO-based SQC has been used to optimize only one parameter in each iteration, resulting in a shorter time for completing the optimizing processes of the SQC.Furthermore,we have simulated the classification tasks with the GFObased SQC, and have compared the results with those using the Adam-based SQC and QSVM.The simulation results have shown that the GFO-based SQC has obtained a higher accuracy and a shorter optimizing time than the Adam-based SQC and QSVM.Additionally,the GFO-based SQC has a good performance in noisy environments.

For further work,we will focus on how to increase the expression power of quantum circuits where parameters can be optimized by this GFO-based SQC for other complex classification tasks.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.62375140) and Postgraduate Research & Practice Innovation Program of Jiangsu Province(Grant No.KYCX19 0900).