Cu-Zn原电池标准电动势测定实验的计算化学设计
2023-11-02刘宇昂刘晓红李姝叶世海李国然言天英
刘宇昂,刘晓红,李姝,叶世海,李国然,言天英
南开大学材料科学与工程学院,天津 300350
近年来,随着量子化学理论的不断完善和计算机技术与计算化学软件的发展,计算化学已逐渐与实验化学、理论化学一起并称化学科学的三个重要支柱,在材料、催化、生物和医药等领域都已获得广泛应用。许多化学教育工作者都希望借助计算化学方法来解决化学实验教学中遇到的各种问题,因此使学生学习并掌握一定计算化学实验技能变得愈发必要与迫切。目前,国内很多高校纷纷开设了计算化学实验课程[1-3],设计了一系列面向高年级本科生的计算化学实验,这些教学实践不仅有助于学生了解和掌握计算化学的基本原理、方法和应用,还有助于学生加深对一些复杂抽象的化学理论知识的理解。
计算化学实验是在计算机上开展的以分子模拟为工具,通过“理论、计算、实验”协同作用来解决各种科学问题的实验。计算化学实验具有教学成本低和实验安全性高的优点,可以帮助学生直观、深入地学习与掌握微观抽象的物理化学基本概念。“电动势的测定”实验为南开大学化学国家级实验教学示范中心面向化学、材料及环境等学科专业本科生开设的一个经典的物理化学实验,采用补偿法(对消法)原理[4]线下开展实验。借助教育信息化的机遇,通过在Cu-Zn原电池电动势的测定物理化学实验中应用信息化技术手段,以计算机作为实验工具,学生通过操作计算机上的Gaussian 16[5]软件,结合物理化学基本理论自主完成实验。本实验可实现信息化技术与实验课程教学高度融合,突破时间与空间的限制,有效帮助学生加深对热力学循环、吉布斯自由能、电极电势、能斯特方程和电池电动势等基本概念的理解,对学生后续的课程学习及日后从事科研工作都有所帮助,为高端技术人才培养提供基础支撑。
1 实验目的
(1) 掌握Gaussian 16软件的基本使用方法,能用密度泛函方法进行理论计算,用基于密度的溶剂模型(Solvation Model Based on Density,SMD)对溶剂化自由能进行计算。
(2) 设计合理的热力学循环来求解热力学量。通过模拟得到的溶剂化自由能,结合升华能、电离能实验值,计算出Cu-Zn原电池的标准电动势。
(3) 加深对标准摩尔吉布斯自由能、电极电势、电池标准电动势等概念的理解。
2 实验原理
2.1 Cu-Zn原电池标准电动势的求解方法
Cu电极和Zn电极都具有较高的交换电流密度值,由它们构成的原电池可逆性比较好。按文献[6]数据,Cu/Cu2+和Zn/Zn2+的交换电流密度均为0.2 A·m-2,两个反应相对较大的交换电流密度,意味着它们的可逆性都比较好,在有相对小的电流通过电极时,电极电位基本保持不变,因而Cu-Zn原电池的电动势比较稳定。本文中Cu-Zn原电池由热力学平衡态的电极构成,可视为可逆电池,其电动势的计算遵循能斯特方程[7]:
在所有组分活度都为1 mol·dm-3的标准状态下,E=EӨ。电池的标准电动势为正、负极的标准电极电势之差,可利用电池反应的标准摩尔吉布斯自由能变与电池标准电动势之间的关系[8]进行计算,其计算式为:
式(2)中z为1 mol电极反应中得失电子的数目,F为法拉第常数,分别表示正、负极相对于标准氢电极SHE的标准电极电势,分别表示正、负极的标准绝对电极电势。
2.2 电极反应的标准摩尔吉布斯自由能变
由式(2)可知,欲求Cu-Zn原电池的标准电动势EӨ,只需求得电极反应(I)和(II)的以的计算为例的计算方法同理),设计了一个热力学循环,如图1所示。
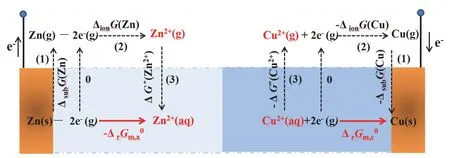
图1 Cu-Zn原电池正、负极反应的热力学循环示意图
在图1中Cu电极一侧,过程(1)表示从Cu(g)转化为Cu(s)的过程。Cu(s)的升华吉布斯自由能可通过计算得到,其中即为Cu(g)的标准生成焓,分别为Cu(g)和Cu(s)的标准熵。则过程(1)的吉布斯自由能变为-ΔsubG。过程(2)为Cu2+(g)转化为Cu(g)的过程。此过程的吉布斯自由能变值即为Cu(g)的电离能相反值过程(3)为Cu2+(aq)转变为Cu2+(g)的过程。此过程的吉布斯自由能变为Cu2+(g)的溶剂化自由能ΔG*(Cu2+)的相反值-ΔG*(Cu2+)[11]。
可得:
根据图1中的热力学循环,将实验得到的热力学数据ΔsubG、ΔionG和按照式(3)进行计算,得到Cu、Zn电极发生还原反应时的标准摩尔吉布斯自由能变(表1)。
表1 ΔsubG,ΔionG和相应电极反应的

表1 ΔsubG,ΔionG和相应电极反应的
* /eV [11] ΔrGm,c,exp电极 ΔsubG/eV [9] ΔionG/eV [10] ΔGexp Ө/eV ΔrGm,a,exp Ө/eV Cu 3.0836 28.0188 -21.7335 -9.3689 -Zn 0.9822 27.3589 -21.1638 - -7.1774
查文献[12]中的标准电极电势表得到Cu、Zn电极在25 °C时标准电极电势分别为和故查表得到的Cu-Zn原电池标准电动势为:
通过上述计算,可知依据热力学循环计算的Cu-Zn原电池标准电动势的相对误差为:
对比文献[9-11]中实验测得的热力学数据实验值(表1)计算得到的Cu-Zn原电池的标准电动势值(1.0958 V)与文献[12]中查到的Cu-Zn原电池的标准电动势的值可知,相对误差仅为-0.62%,表明通过热力学循环求解Cu-Zn原电池标准电动势的方法具有正确性。
2.3 Gaussian量化计算软件
Gaussian软件是目前使用较广泛的一款量子化学计算软件,其最新版本是Gaussian16。Gaussian软件通常包括用于计算的Gaussian和用于图形界面处理的GaussView两个组件。其中Gaussian软件涵盖了从头算方法、密度泛函方法和半经验方法等多种计算方法[13]。密度泛函理论基于Hohenberg-Kohn定理,将3N维多电子波函数问题简化为3维电子密度问题,用电子密度分布函数求解薛定谔方程,从而得到系统总能量及相关性质。Gaussian中,可通过对优化好的结构进行频率分析,进而计算分子的内能、焓、吉布斯自由能等热力学量。Gaussian中吉布斯自由能的计算过程为G=Eele+Gcorr,其中Eele为单点能,即分子的电子能量,包括电子的动能、电子与原子核间的势能、电子之间的相互作用能以及原子核之间的相互作用能;Gcorr则是温度与压力的影响所带来的吉布斯自由能修正项。由于实验上许多构成电池的分子与离子的溶剂化自由能较难直接测得,故本实验采用Gaussian计算方法得到离子的溶剂化自由能,进而计算出Cu-Zn原电池的标准电动势。
实验中Cu2+的溶剂化自由能是通过Gaussian计算的Cu2+溶液相的吉布斯自由能(Gaq)与气相吉布斯自由能(Gg)相减得到。因为气相和溶液相的Gcorr通常相差不大,故不需要做溶剂模型下的频率分析来获得而只做单点能计算,用溶液相单点能Eele(aq)与气相单点能Eele(g)相减即得到本实验中,使用Gaussian16计算Cu-Zn原电池标准电动势的过程如图2所示。
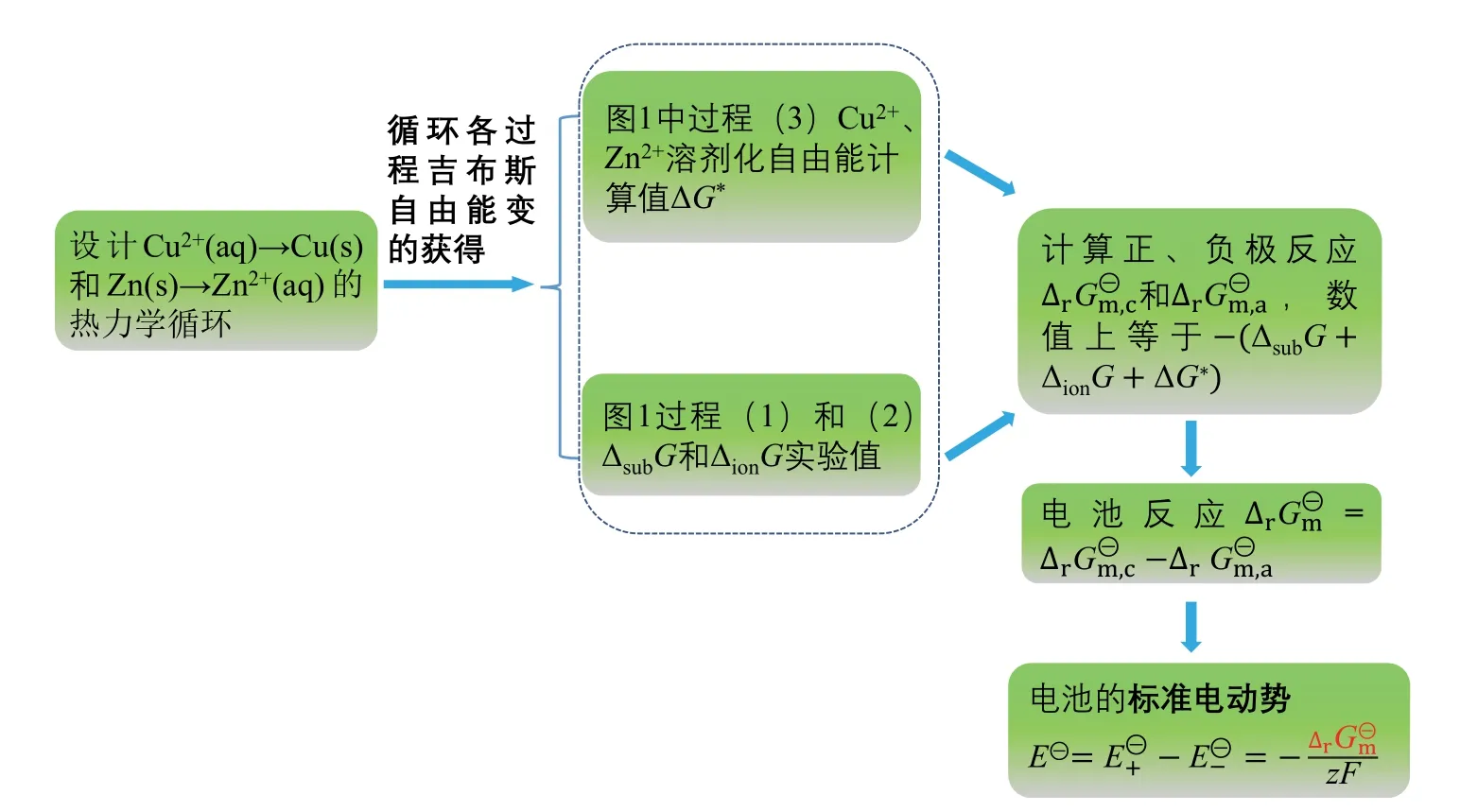
图2 Cu-Zn原电池标准电动势计算过程流程示意图
3 实验设备
Gaussian 16软件,GaussView 5.0软件,DELL台式电脑(处理器:i5-6500;核心数:4;运行内存:32GB)。
4 实验步骤
4.1 用M06-2X/6-31G(d)密度泛函方法和SMD模型进行单点能的计算
构建初始结构,打开GaussView,点击Cu原子,保存为输入文件(*.gjf),采用M06-2X/6-31G(d)密度泛函方法,对Cu2+进行单点能的计算。M06-2X属于Truhlar课题组开发的明尼苏达泛函系列,是采用广义近似梯度的杂化密度泛函之一[14]。6-31G(d)是基组的名称,表示内层轨道用6个Gauss型函数(GTO)拟合1个Slater型函数(STO),这1个STO拟合1个原子轨道,价层轨道分为内(I)、外(O)轨道,内层轨道用3个GTO拟合1个STO(I),外层轨道用1个GTO拟合一个STO(O),然后1个STO(I)和STO(O)拟合一个价层原子轨道;在6-31G基组的基础上给重原子添加了d轨道极化函数。
编辑输入文件,Gaussian中默认的计算项目即单点能计算,因此计算单点能时关键词sp可不写。Gaussian默认状态为气相的计算,不需额外增加关键词,溶液相的计算则需要添加溶剂模型。溶剂模型包括隐式溶剂模型和显式溶剂模型,前者不考虑溶剂分子的实际结构,只把溶剂视为具有一定介电常数的连续介质,后者则是计算时在体系中直接增加溶剂分子,考虑溶质与溶剂分子间的相互作用以及溶剂分子的不同排布方式,这会导致计算量大幅增加。本实验采用的SMD溶剂模型[15],是由Truhlar及其合作者发展的一种参数化的基于SCRF的隐式溶剂化模型,该模型已经用2821个溶剂化数据的训练集进行了参数化,包括112个水性离子溶剂化自由能。Gaussian中使用scrf关键词来调用溶剂模型,因此在计算执行命令行关键词中需添加“scrf=SMD”,因SMD模型默认的溶剂为水,故“solvent=water”可不写。在电荷与多重度行,Cu2+的电荷为+2,有一个单电子,因此电荷和多重度设置为“2 2”。Cu2+的坐标直接设定为“0.0 0.0 0.0”,气相单点能计算输入文件如表2所示。溶液相单点能计算的输入文件只需将表2中执行命令行关键词中加上“scrf=SMD”。

表2 Cu2+气相单点能计算输入文件
输入文件编辑完成后,点击GaussView中“Calculation”下拉菜单“Gauss Calculation Setup”命令进入设置Gaussian计算选项,点击“Submit”选项,提交计算任务,也可通过在Gaussian软件中打开已建立的输入文件,进行计算任务提交。计算完成后会得到单点能计算的输出文件(*.log,若用Gaussian软件直接提交计算,则输出文件格式为*.out)。用文本编辑器打开输出文件,在“HF=”处读取Cu2+和Zn2+气相和溶液相的单点能数据。
4.2 Cu2+和Zn2+溶剂化自由能的计算
由4.1小节中提取的Cu2+和Zn2+气相和溶液相单点能数值,计算得到它们的溶剂化自由能因为SMD溶剂化自由能是指从298.15 K的理想气体到298.15 K理想溶液的自由能变化,并且在气相和溶液相中使用相同的浓度(1 mol·L-1)。但本实验所选取的状态是标准状态,为气相pӨ下溶质到1 mol·L-1溶液相状态过程的自由能的变化,因此需要加上修正项,修正项的计算为:
所以,
4.3 Cu-Zn原电池标准电动势的计算
将Gaussian计算得到的溶剂化自由能与查到的原子升华自由能[9]和电离自由能变[10]按式(3)进行计算,可以得到Cu电极发生还原反应时的标准吉布斯自由能同理,Zn负极侧的计算过程如同进而计算得到Cu-Zn原电池反应的标准摩尔吉布斯自由能变化,再由式(2)可计算出Cu-Zn原电池的标准电动势。
5 结果与讨论
由于Cu2+与Zn2+所带电荷量相同,离子半径相近,实验测得二者的溶剂化自由能相近,这与本实验的Gaussian计算结果见表3)相一致。两种离子溶剂化自由能的Gaussian计算值与实验测得的溶剂化自由能值,见表1)相比有所偏差,可能是由于Gaussian计算中选用的SMD溶剂模型,忽略了离子的真实溶剂化结构造成的。
表3 Cu2+和Zn2+溶剂化自由能的量化计算值以及相应电极反应的

表3 Cu2+和Zn2+溶剂化自由能的量化计算值以及相应电极反应的
*1 hartree = 2625.5 kJ·mol-1 = 627.51 kcal·mol-1 = 27.21 eV
Ө /eV Ө /eV ΔrGm,a物种 Eele(g)/hartree * Eele(q)/hartree ΔGcal* /eV ΔrGm,c Cu2+ -1639.16842165 -1639.91593249 -20.2578 -10.8446 -Zn2+ -1778.07288886 -1778.82510413 -20.3858 - -7.9553
根据表3中Gaussian计算的溶剂化自由能,可计算得到Cu-Zn原电池电极反应的值,进而得到电池总反应的通过式(2)可得到其标准电动势为:
根据文献[16],考虑到Cu2+添加一些显式的溶剂水分子,再对Cu2+的水合团簇使用SMD模型计算团簇的溶剂化自由能,利用热力学循环便能求出Cu2+的溶剂化自由能。此方法称为团簇连续化溶剂模型,是一种结合了显隐式溶剂模型的混合溶剂模型,考虑了溶质分子真实的溶剂化结构,使溶剂化自由能的计算结果更精确。因此,在使用量化软件进行计算时,不仅需要正确的理论方法,还需要选用合适的模型。
6 思考与拓展阅读
1) 根据计算结果得知本实验的误差主要来自于离子溶剂化自由能的计算过程,请思考原因。尝试更换计算方法,看能否解决这个问题。
2) 请阅读文献[16],尝试用团簇连续化溶剂模型计算Cu2+和Zn2+溶剂化自由能,并与实验值进行比较。
7 结语
本实验以计算机作为实验工具,发展了经典的“电动势的测定”这一物理化学实验。在实验中,学生可通过操作Gaussian 16软件线上开展Cu-Zn原电池标准电动势的测定实验,可与线下实际操作互补结合。学生通过自主设计热力学循环,计算出原电池反应的标准摩尔吉布斯自由能变,进而得到Cu-Zn原电池的标准电动势。此实验可实现现代化信息化技术与实验教学有效融合,帮助学生加深对标准摩尔吉布斯自由能、电极电势以及电池电动势等基本概念的理解,引导学生进行发散思维,感悟计算方法中严密的逻辑关系,有利于提高学生分析解决问题能力、科学研究能力与动手实践能力。
