基于ARIMA-OSELM的火电厂SCR入口NOx浓度预测建模研究

2023-11-02金秀章陈佳政李阳峰

计量学报 2023年9期

金秀章, 陈佳政, 李阳峰

(华北电力大学控制与计算机工程学院，河北保定071003)

1 引言

目前,火力发电仍是我国发电的主要支柱,而发电过程中产生的氮氧化物(NOx)又是大气中NOx污染的主要来源之一。因锅炉燃烧过程运行工况复杂,反应延迟较大,致使选择性催化还原(selective catalytic reduction)烟气脱硝系统(下文简称SCR)入口NOx浓度无法准确地即时测量,从而使喷氨量无法准确中和NOx[1]。因此建立精准高效的预测模型来满足对NOx排放浓度的实时监测具有重要意义。

目前我国大部分电厂使用连续排放监测系统(continuous emission monitoring system, CEMS)对NOx的排放进行监测,其测量方式为直接抽取排放烟气进行测量,但这种测量方法难以保证结果的实时性[2]。现针对NOx排放预测的建模方式包含反应机理建模和以数据驱动为基础的建模2种。电厂发电过程极为复杂,其燃烧过程包含大量的物理化学反应,同时反应过程中的各类扰动也影响模型参数的确定,因此大大增加了机理建模难度[3]。近年来,随着机器学习的快速发展,基于数据驱动的“黑箱”建模进入了大众视线,其建模过程相对简单,因此大受研究者们的喜爱。吕游等[4]利用最小二乘支持向量机建立了NOx排放预测模型,与支持向量机相比,提升了模型的泛化能力;Fu等[5]利用长短期记忆网络(LSTM)建立了脱硫效率预测模型,预测精度较高。大量研究表明,加入时间序列预测方法的混合模型的建立能够弥补神经网络模型对数据中线性部分预测结果较差这一缺陷,其混合模型的互补特性能够有效地分析数据中线性和非线性的部分,提高了模型的预测精度。卢建昌等[6]建立了时间序列法和神经网络相混合的预测模型,大大提高了模型的预测精度;范京道等[7]建立了时间序列分析和支持向量机相结合的瓦斯浓度预测混合模型,预测结果明显优于单一模型。

本文利用混合模型中优势互补的原理,提出了一种基于自回归滑动平均模型(autoregressive integrated moving average,ARIMA)和在线贯序极限学习机(online sequential extreme learning machine,OSELM)相混合的组合预测模型,并以2种组合方式:最优权重法和残差优化法,构建SCR入口NOx预测模型。利用现场实际运行数据对模型进行对比验证分析,并与单一ARIMA模型和OSELM模型进行对比,以期为电厂SCR系统NOx排放浓度监测提供参考。

2 基本原理

2.1 自回归滑动平均模型

自回归滑动平均模型是时间序列预测分析方法之一,在时间序列数据分析中流行且广泛使用[8]。其模型表示为ARIMA(p,d,q),其中,AR代表自回归,p为自回归项数;MA代表滑动平均,q为滑动平均项数;d代表平稳序列的差分阶次,表达式为:

yt=θ0+φ1yt-1+…+φpyt-p+εt-

θ1εt-1-θ2εt-2-…-θqεt-q

(1)

式中:yt和εt分别为t时刻的实际值和随机误差,εt需符合正态分布;φt(t=1,2,…,p),θj(j=1,2,…,q)为模型参数,p和q为模型阶数。

一般的,ARIMA模型的建模步骤如下:1) 对时间序列进行平稳性检验,若序列检验不通过,则对其进行差分运算。通常情况下,一阶差分即可得到平稳序列,差分阶次过高,会导致数据信息损失,不利于模型的建立;2) 采用贝叶斯信息准测(BIC)[9]来确定模型中p和q的阶数,BIC值越小说明模型效果越好;3) 使用确定好的模型阶数对时间序列进行拟合,并使用极大似然估计法对模型参数进行估计;4) 进行残差检验,查看残差是否符合正态分布,如果不符合正态分布则需重新确定p、q值再次进行定阶;5) 通过检验后进行预测和误差分析。建模流程如图1所示。

图1 ARIMA模型建模步骤流程图Fig.1 ARIMA model modeling step-by-step flowchart

2.2 在线贯序极限学习机

与传统的单隐藏层前馈神经网络不同,极限学习机(ELM)选取输入权重和隐藏层偏置是随机的,通过最小化由训练误差和输出层权重范数的正则项构成的损失函数,反向计算出输出层权重,在训练过程中只需要提前设置隐含层神经元个数。ELM相比于其他神经网路具有训练参数少、学习速度快、泛化能力强等优点[10]。

ELM训练网络过程如下:

1) 给定训练集Z=(X,T),X=[x1,x2,…,xd],T=[t1,t2,…,tm],其中xi=[xi1,xi2,…,xin]∈Rn表示输入数据;ti=[ti1,ti2,…,tin]∈Rn表示输出数据,隐含层节点数为L,激活函数为Sigmoid函数,随机初始输入权重和隐含层偏置。

2) 计算隐藏层输出H(x),表达式为

H(x)=[h1(x),…,hL(x)]

(2)

式中:hi(x)是第i个隐藏层节点输出,计算式如下:

hi(x)=g(wix+bi)

(3)

式中:wi是输入权重;bi是隐藏层偏置;g(x)是激活函数。

3) 求解出隐藏层与输出层之间的输出权重β,定义广义单隐层ELM输出为:

(4)

式中:β=[β1,β2,…,βL]T;T是训练数据的目标矩阵。

为保证训练误差最小,使用最小化近似平方差的方法对β进行求解,目标函数如下:

(5)

β可以通过β=H*T来求得,其中H*为隐含层输出矩阵H的广义逆矩阵。

在线贯序极限学习机(OSELM)是在ELM的基础上演变出来的一种增量学习算法,其本质为分批次数据学习。OSELM具有极限学习机本身的训练速度快,泛化能力强的优点,同时它还可以根据新导入的数据实现模型参数的在线更新。OSELM的在线学习主要包括2部分:

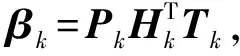
(6)

Tk=[t1,t2,…,tk]T

(7)

2) 在线学习阶段:输入第k+1组数据,计算相应的隐藏层输出矩阵Hk+1(x),输出权值更新公式如下:

(8)

式中:Pk+1更新公式如下:

(9)

令k=k+1,继续进行在线学习,并不断更新网络参数,直至训练完毕。

2.3 ARIMA-OSELM组合预测模型

锅炉燃烧系统极为复杂,参与燃烧反应的辅助变量较多,故NOx浓度时间序列包含线性部分和非线性部分,使用单一ARIMA或OSELM无法精准地预测NOx浓度[11]。由模型结构可知,ARIMA模型对于序列中线性部分的预测更加准确[12],OSELM模型则对非线性部分的数据更加敏感,其二者之间存在优势互补的特点,所以将2种模型组合使用,更能发挥各自优点,提高模型的精确度。本文从2个角度:最优权重组合和残差优化组合进行研究,构建ARIMA-OSELM组合预测模型,对火电厂实际运行数据展开验证,最后与单一ARIMA和OSELM模型数据进行对比。

2.3.1 最优权重组合预测方法

使用单一ARIMA和OSELM模型分别进行建模预测,以组合模型预测结果的最小误差平方和为优化目标,构建数学优化问题模型求得组合权重,最终得到组合预测结果。组合模型预测结果表达式为:

Yt=k1x1t+k2x2t

(10)

式中:k1,k2分别为ARIMA模型和OSELM模型的权重系数;x1t为ARIMA模型在t时刻的预测结果,x2t为OSELM模型在t时刻的预测结果;Yt为组合模型在t时刻的预测结果。最优权重组合法的重点就是根据误差求取权重系数k1,k2。组合模型的误差表达式为:

et=k1e1t+k2e2t=(k1x1t+k2x2t)-x0t

(11)

式中:et、e1t、e2t分别为组合模型在t时刻预测误差、ARIMA模型在t时刻预测误差、OSELM模型在t时刻预测误差;x0t为在t时刻实际观测值。

通过建立数学优化问题模型求取加权系数是较为流行的方法之一,现以组合模型误差平方和最小为优化目标,建立优化问题模型如下:

(12)

式中:m为时间序列长度。此处采用拉格朗日乘子法求得k1,k2:

(13)

(14)

最终基于ARIMA-OSELM组合模型的预测值为Yt=k1x1t+k2x2t。该预测方法的流程图如图2,具体步骤如下:

1) 首先对NOx浓度时间序列的平稳性进行检验,确定ARIMA模型的差分次数d;然后使用贝叶斯信息准则(BIC)确定模型阶数p和q;利用最小二乘法确定模型表达式参数,将NOx浓度时间序列放入ARIMA模型中得到预测结果x1t。

2) 以前3 000组数据作为作为OSELM模型训练集,后600组数据作为模型的测试集;将前3 000组数据放入OSELM模型进行训练,得到网络权值参数,建立OSELM模型,将测试集放入模型得到OSELM预测结果x2t。

3) 利用最优权重组合方法确定组合权重值k1,k2,得出最终预测结果Yt=k1x1t+k2x2t。

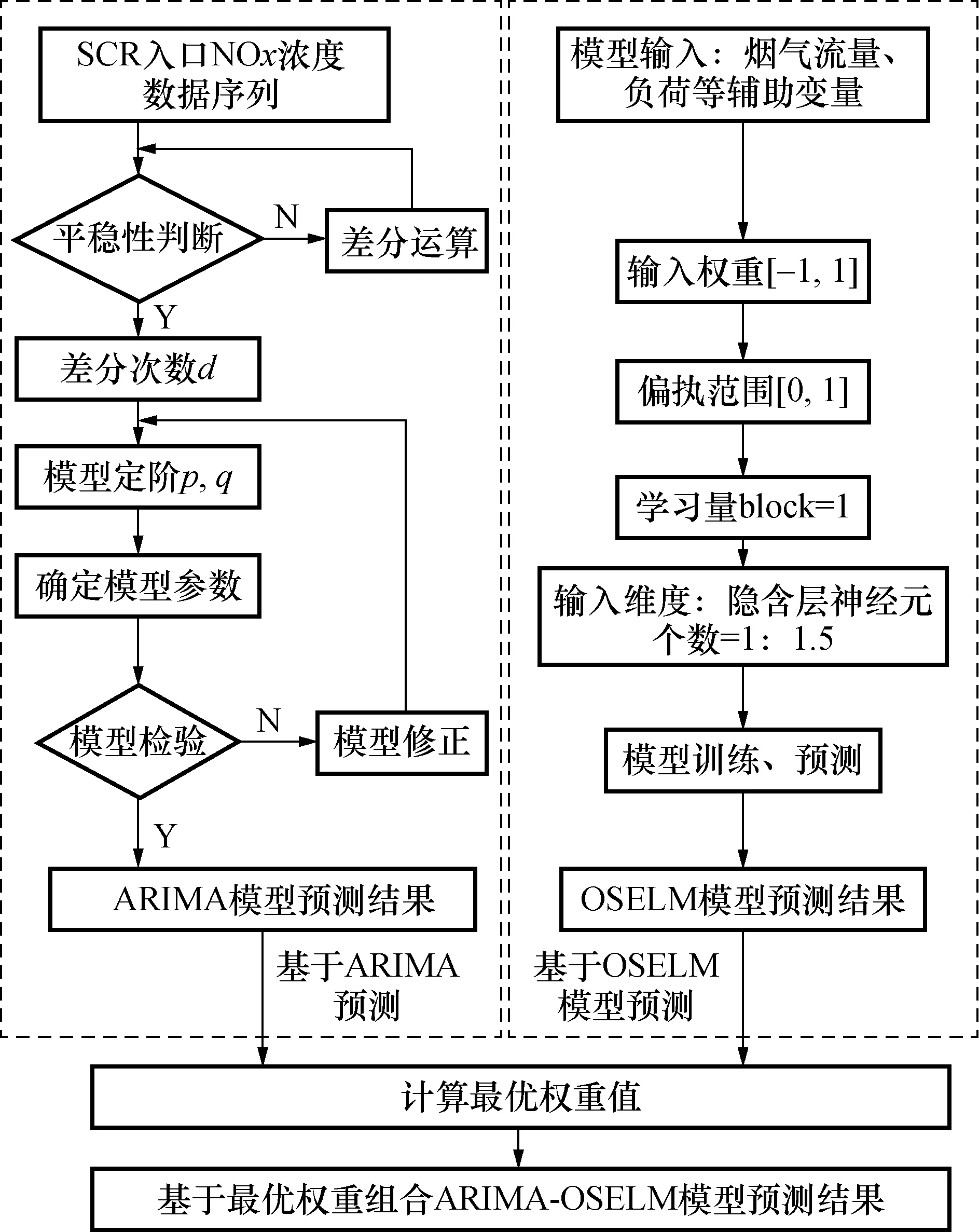
图2 基于ARIMA-OSELM神经网络最优权重组合预测模型Fig.2 Optimal weight combination prediction model based on ARIMA-OSELM neural network

2.3.2 残差优化组合预测方法

首先使用ARIMA模型对SCR入口NOx浓度序列中的线性部分进行预测,得到预测值为x1t,SCR入口NOx浓度实际序列为xt,则误差表达式即为e=xt-x1t。误差et中包含辅助变量:烟气流量、负荷等非线性因素对NOx浓度的影响,再利用OSELM对NOx浓度中的非线性部分进行预测,预测结果为x2t,则此时ARIMA-OSELM组合模型的预测结果即为x2t,该方法流程如图3所示:

(1) 首先对NOx浓度时间序列的平稳性进行检验,确定ARIMA模型的差分次数d;然后使用贝叶斯信息准则(BIC)确定模型阶数p和q;最后利用最小二乘法确定模型表达式参数,将NOx浓度时间序列放入ARIMA模型中得到预测结果x1t。

(2) 将ARIMA模型预测结果x1t与实际时间序列xt相比较,得到预测误差et=xt-x1t。

(3) 把预测误差et和辅助变量作为OSELM模型的输入,对模型进行训练得到网络权值参数,建立OSELM预测模型,再将测试集放入模型中,得到预测结果x2t,即最终预测结果。

图3 基于ARIMA-OSELM神经网络残差优化组合预测模型Fig.3 Optimized combinatorial prediction model based on ARIMA-OSELM neural network residuals

3 NOx浓度预测模型建立

3.1 数据的时延分析及特征选择

实验数据为某电厂现场运行数据,共截取3 600组,采样周期为5 s,总选取时间为5 h。其中前 3 000组数据进行训练,后600组数据进行测试。根据NOx生成机理初步选择出14个辅助变量,包含:机组负荷、总煤量、A/B层给煤机电流转速、SCR入口烟气含氧量、SCR入口烟气温度、总风量、锅炉含氧量、尿素阀门开度、SCR入口烟气流量、炉膛负压和尿素流量。原始数据包含一些异常值,故先将数据进行预处理,此处采用拉依达法则对数据进行异常值替换。后对数据进行归一化处理,以保证各参数之间量纲相同,提高模型预测精度。

由于锅炉燃烧过程具有大迟延的特性,所以在现场运行过程中采集到的各个点位的相关数据与SCR入口NOx浓度实时数据存在一定的时间偏差。本文设计了一种基于最大互信息[13]的时延计算方法,选取相关性最大的一时刻作为时延补偿,从而确定最终变量输入序列。锅炉燃烧过程参与反应变量较多,各辅助变量之间存在冗余,且过多变量输入模型后会造成模型复杂度变高,甚至出现模型的过拟合,所以需要对辅助变量进行筛选,以提高模型预测精度。现利用mRMR[14]算法对所有辅助变量进行变量筛选以剔除冗余,最终得到7个辅助变量,分别为:SCR入口烟气温度、SCR入口烟气含氧量、烟气流量、尿素流量、负荷、给煤机电流、炉膛负压,将其作为模型的最终输入。表1为各变量迟延的时间。

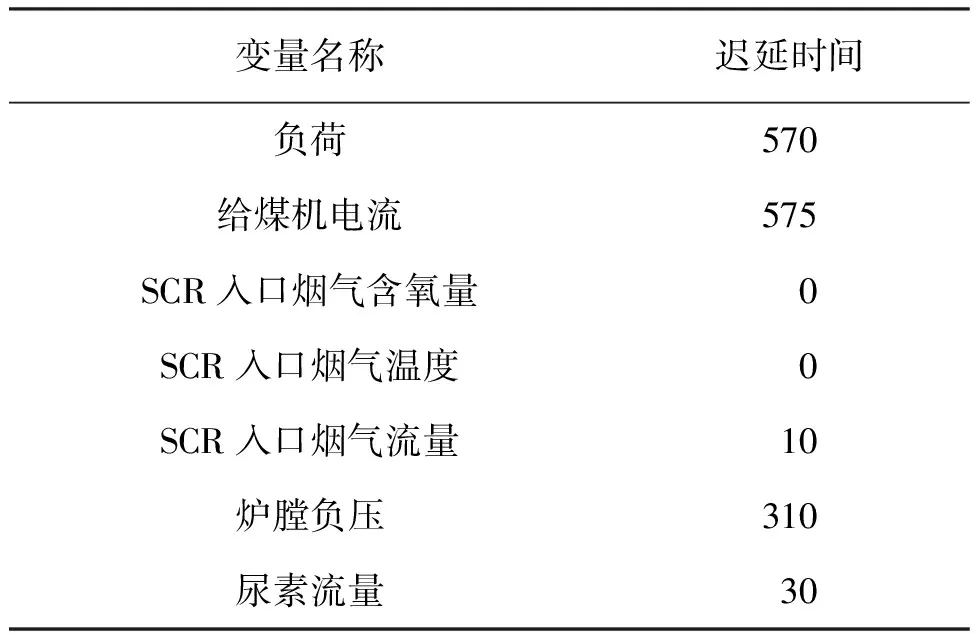
表1 变量迟延时间表Tab.1 Variable Latency Schedule s

3.2 ARIMA模型参数确定

ARIMA模型预测前,需对时间序列进行平稳性检验、模型定阶和残差检验。

3.2.1 平稳性检验

常用于时间序列平稳性检验的方法有自相关和偏自相关图法(autocorrelation coefficient-partial autocorrelation coefficient,ACF-PACF)[15]、单位根检验法(augmented dickey-fuller test,ADF)[16]。ACF-PACF法核心是自相关函数和偏自相关函数,通过观察自相关、偏相关函数的残差分布图是否在95%置信区间内,以及函数拖尾、截尾情况来判断序列是否平稳,其缺点是当时间序列数据量较多,模型较为复杂时不能够客观地判断出序列的平稳性,所以,本实验使用ADF单位根检验法。

首先假设所处理时间序列存在单位根,即非平稳序列,若求得的统计量(augmented dickey-fuller test statistic,ADF-TS)的值远小于置信空间的临界统计值(1%、5%和10%),且P值小于显著性水平0.05,则为拒绝假设,即所使用时间序列为平稳序列。若序列为非平稳序列,则需对序列进行差分运算,但实际操作中,差分运算次数不宜过多,以避免序列中信息损失严重。

将实验所用时间序列绘制图像,如图4(a)所示。通过图像可直观判断出,此时序列较为凌乱,且无法观测出其整体趋势,故初步判定为非平稳序列。使用ADF单位根检验法进一步验证,此时P值为0.013,大于显著性水平0.05,说明无法拒绝该假设,即序列为非平稳序列;对序列进行一阶差分运算,结果如图4(b)所示。从图中可以看出,此时序列围绕着一个常数上下波动,经过ADF单位根检验计算此时P值为0.001,小于0.005,结果为拒绝原假设。所以经过一阶差分运算后序列变为平稳,即ARIMA(p,d,q)中d=1。

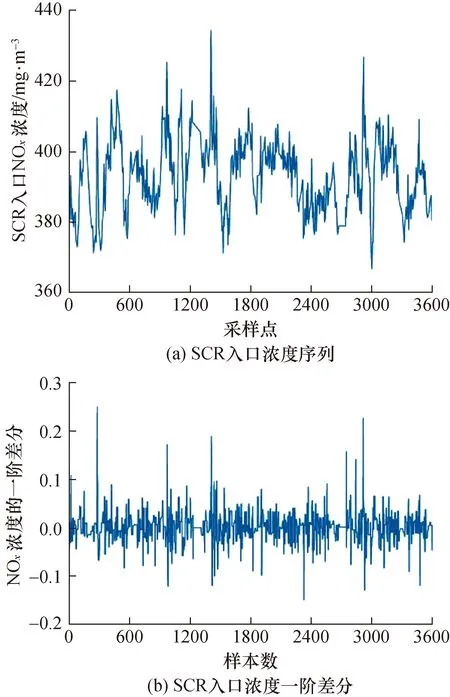
图4 NOx浓度序列和一阶差分Fig.4 NOx concentration sequence and first-order differential

3.2.2 模型定阶

使用BIC准则[17]对模型的p,q定阶,BIC准则表达式为:

BBIC=mln(n)-2ln(L)

(15)

式中:m为模型参数个数;n为样本数量;L为似然函数。BBIC值越小,表明模型的拟合度越高,即预测结果越好。绘制平稳序列自相关和偏自相关函数图,见图5。

图5 ACF-PACF函数图Fig.5 ACF-PACF function diagram

图5中自相关函数明显拖尾,偏自相关函数图拖尾或者5阶截尾,无法判断其准确值。所以有可能ARIMA模型阶数为p=5,q=0,即ARIMA(5,1,0)。但序列数据量较大,且用ACF-PACF图像法来确定p、q值并不完全准确,所以需要继续使用BIC准则法进一步确定p,q阶数。取p,q的取值范围为1～5,共25组模型进行BIC准则测试,表2为各模型BIC准则计算值,横向为q,纵向为p。由表格可得,其中最优模型选择经计算得p=3,q=3时的BIC值最小,所以最终时间序列模型为ARIMA(3,1,3)。

表2 BIC准则表Tab.2 BIC criteria table

3.2.3 模型检验

在正式预测之前,需要对模型进行残差检验。残差需要满足均值为0,方差为常数的正态分布且不满足自相关性。现对残差序列进行正态分布检验和Durbin-Watson(DW)检验[18],DW统计是计量经济学分析中最常用的自相关度量。若残差符合正态分布图像,且DW检验值接近2,则说明检验通过,可以进行下一步预测。图6为标准化残差图和正态分布图,由图6(a)可看出大部分残差落到(-5,5)区间内,基本服从正态分布,图6(b)能够更加直观地看到残差序列符合正态分布。经过计算,DW检验值为1.999 6,接近2。综上可以确定,残差序列满足正态分布并且不存在自相关性,即所用模型可以较好地预测本次实验数据。

图6 标准化残差和正态分布图Fig.6 Standardized residual and normal distribution plots

3.3 OSELM参数确定

设置Sigmoid函数为OSELM模型的激活函数;输入权重的范围为[-1,1];隐含层偏置的范围设置为[0,1];模型在线学习是步长设置为1;模型试验过程中,利用交叉验证和网格搜索算法确定初始化训练样本数量以及隐含层神经元个数(保证N0≥L[10])。经过多次实验对比,模型输入维度:隐含层神经元个数=1:2时,模型预测效果最佳。

3.4 模型评价指标

模型采用的评价指标为FMAPE、MRMSE和R2:其中FMAPE表示预测序列较真实值序列的平均偏离百分比,其值越小说明模型预测精度越高;MRMSE为均方根误差,表示预测值与真实值之间的标准偏差的大小,数值越小表明预测精度越高;R2为决定系数,表示预测值相对真实值的偏离程度,其数值越接近于1,表明预测效果越好。将三者结合使用能够更全面地评价预测模型的好坏,计算式如下:

(16)

(17)

(18)

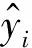
4 实验结果与分析

4.1 辅助变量筛选对预测结果的影响

为验证mRMR算法对变量筛选后的有效性,现建立对比模型实验,分别以全部辅助变量和经过mRMR筛选后的辅助变量为模型输入对SCR入口NOx浓度进行预测,其余实验条件均不变。图7为变量筛选前后预测效果图,表3为对应的预测结果评价指标。

由图7和表3可知,经过筛选后的变量放入模型后,使得模型预测精度有了明显提高。相比于筛选前模型预测结果,模型FMAPE下降了28%;R2提高了26%;MRMSE下降了37%。以上数据表明,模型输入变量之间存在冗余关系,将会影响模型预测精度,有效的筛选变量可以减少模型复杂度,提高模型预测精度。

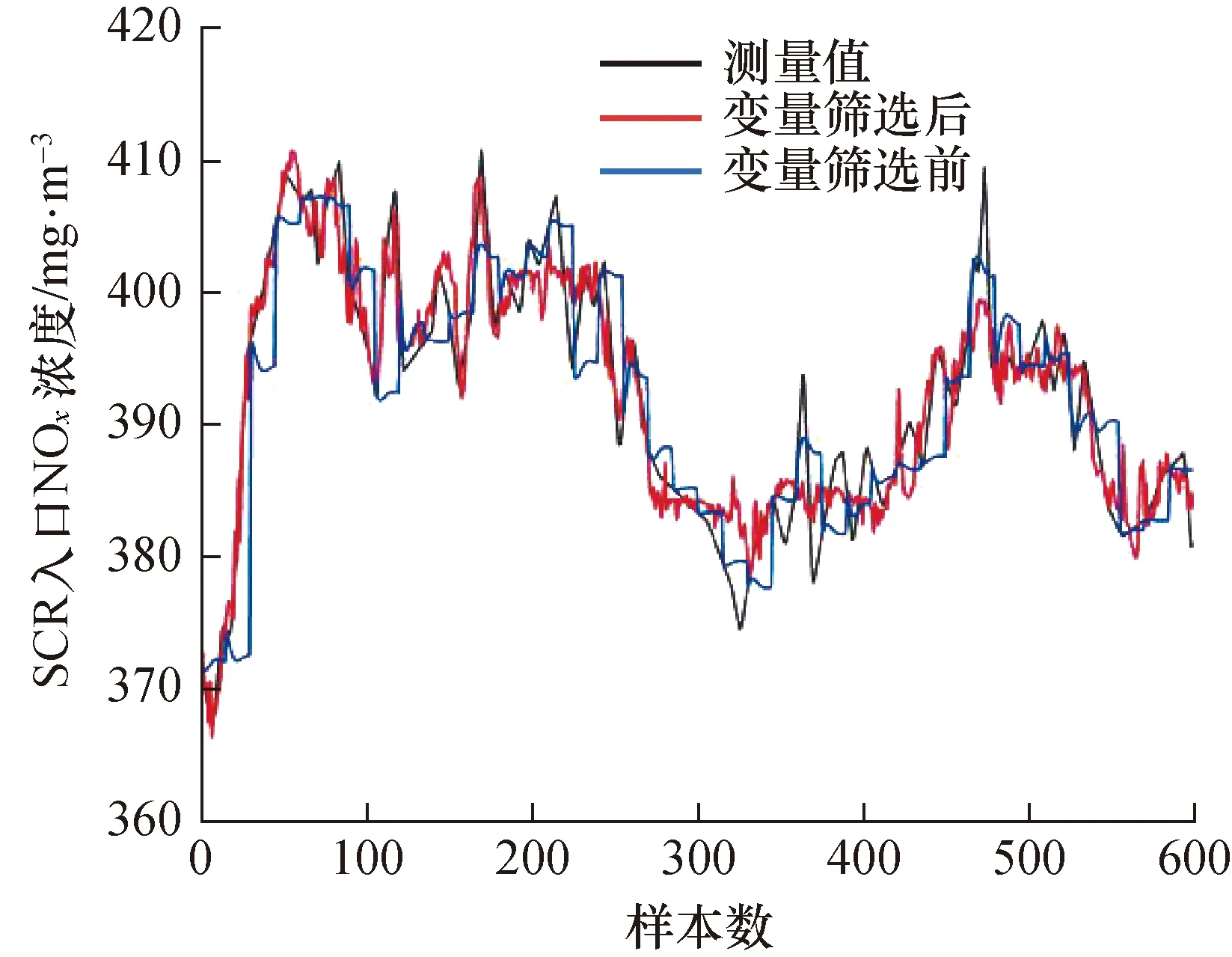
图7 输入变量筛选前后预测结果Fig.7 Enter variables to filter the prediction results before and after

表3 变量筛选前后的模型评价指标

4.2 ARIMA-OSELM组合模型预测与结果对比

现分别使用单一ARIMA预测模型、单一OSELM预测模型、ARIMA-OSELM最优权重组合预测模型和ARIMA-OSELM残差优化组合预测模型这4种模型对SCR入口NOx浓度进行预测。结果显示(见表4),4种模型进行单步预测所花费的时间分别为:2.37×10-6、2.68×10-6、7.31×10-6和8.25×10-6s;所用时间均小于采样周期5 s以及CEMS系统监测时间,证明此预测过程可以用于下一步的闭环控制。模型预测结果曲线图和模型评价指标见表5。

表4 不同模型的预测时间

图8 不同模型预测结果Fig.8 Different models predict outcomes

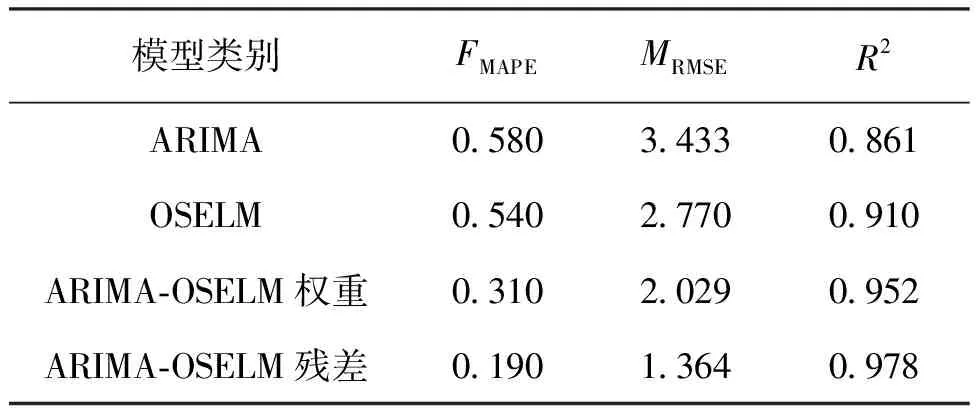
表5 不同模型的模型评价指标

4种模型的预测结果见图8。通过对比可以看出,ARIMA-OSELM组合模型的预测结果拟合曲线明显优于单一ARIMA模型和单一OSELM模型的预测结果拟合曲线,表明对线性数据预测有优势的ARIMA模型和对非线性预测能力较强的OSELM模型经组合后,2个模型的优势进行了互补,提高了模型预测精度,对电厂SCR入口NOx浓度预测是有实际意义的。其中,单一ARIMA模型的误差最大,预测效果也最不理想,结合模型评价指标表4可以看出,各项评价指标均为最差,由此可以说明ARIMA模型对非线性数据的预测确为劣势,此单一模型不适用于复杂度较高的非线性数据的预测。结合图、表进一步分析可知,单一OSELM模型的评价指标较好于单一ARIMA模型,预测效果分别别提升了6.9%、19.3%、5.7%,说明OSELM模型对高维度、高复杂度的非线性数据较为敏感,可以用来预测浓度。基于残差优化组合的ARIMA-OSELM模型的预测结果最优,其FMAPE、MRMSE和R2分别为:0.190、1.364、0.978,相比于最优权重组合预测方法,预测结果分别提升了38.7%、32.8%、2.7%,表明将NOx浓度时间序列中的非线性部分作为模型的输入之一,提取了残差序列中的可用信息,有效地提升了模型预测精度。