基于仿真技术的服装产品开发流程优化策略研究
2023-11-01石春乐杨以雄
石春乐, 杨以雄
(1.福建商学院 管理工程系,福建 福州 350001;2.东华大学 服装学院,上海 200051)
0 引言
在生命周期较短的产品设计中,时间作为核心竞争力,能帮助企业快速响应消费者需求,提高产品研发能力[1]。通过有效管理新产品开发过程的人员、活动、资源、目标,优化产品开发流程,企业能够缩短产品的开发周期时间,减少交货时间的波动,提高准交率[2]。服装产品的生命周期不长,通常注重产品的设计和开发,其主要特点是“快”,以满足需求的不确定性,能够引领产品设计潮流;并且增加消费品种的数量,让销售价格更平民化[3]。
本文以流程优化的创新思维,使用S品牌的系统动力学(system dynamics, SD)仿真模型为例,定量评估其产品开发流程的时间KPI(key performance indicator),构建优化流程的仿真实验平台。从资源配置的角度设计42组仿真实验,通过对仿真模型的主要变量进行局部灵敏度分析[4],找到流程的受阻环节。最后使用麦肯锡(McKinsey)矩阵分析仿真实验结果,为优化产品流程提供有益参考,降低管理决策风险。
1 产品开发流程的仿真模型
1.1 概念模型和仿真模型
E公司在2003年成立,每年营业收入近43亿元,旗下有5个服装品牌(含S品牌)。该公司的产品定位于23~29岁的年轻女性,思想时尚,有一定的经济基础和消费能力,文化素养高,钟爱运动,生活态度积极向上。近年来,S品牌希望通过改善其开发流程,进一步提升产品的时间竞争力。为了建立产品开发流程的概念模型,项目组与S品牌的品牌部、设计部、运营部、技术部等部门经理进行了深度访谈,并详细调查了产品的开发流程和相关数据,明确了具体的研究内容和研究范围。S品牌产品开发流程的概念模型和仿真模型的详细情况,可参见文献[5]。
项目组从中观层面,运用系统动力学建立了S品牌产品开发流程的概念模型[6]。系统动力学描述系统组成及其相互关系的变量主要有3类,分别为存量、流量、参数。存量描述系统中的储存环节;流量描述系统中的活动,即存量变化的快慢;参数定量地描述系统中变量间的因果关系。结合S品牌产品开发的业务流程,本文共定义了71个变量,建立了流程的存量—流量图,如图1所示。

图1 S品牌产品开发流程的存量—流量图Fig.1 Stock-flow chart of S brand products development process
结合产品开发流程的概念模型,用微积分方程进一步定量地描述变量间的因果关系,并用STELLA软件实现了流程的仿真模型。仿真模型的时间单位为天(d),设定的运行期限为两年(730 d),步长DT值为1/4 d。
1.2 变量初始值和时间KPI
如表1所示,运行仿真模型前,需要进行各变量的初始化设置:存量数值通常设为零,流量和参数的数值则源自产品开发流程的实际运营情况,并结合调查情况和历史数据进行核验。仿真模型还设置了4个与时间绩效相关的KPI,分别为准交率DR(delivery rate),周期时间CT(cycle time),周期时间标准差CTS(cycle time STDDEV),平均有效产出MF(mean flow)。
1.3 模型的仿真、确认和验证
仿真模型必须进行确认和验证V&V(verification &validation)。项目组从业务流程、输入数据、建模仿真、输出数据等方面[7]对仿真模型进行V&V核验,并用批均值法对稳态仿真的输出数据进行数理统计与分析验证。实验结果表明,在置信区间范围内,仿真模型的运行结果与实际数值基本吻合。
2 优化流程的仿真实验
2.1 流程时间的阻碍
确认和验证后,即可进行仿真实验。仿真实验的总体思路是:①把各类资源进行数字化,转化为存量、流量、参数等变量,并确定各变量的取值范围;②结合业务流程的实际运营情况,进行资源的分配,定量地研究各输入变量对系统预期产出的影响,从而找到各类资源投入(人力、财力、物力)对时间KPI的影响,提升流程管理的效率与质量,帮助企业进行科学决策[8]。
本文运用局部灵敏度分析方法进行仿真实验。局部灵敏度分析属于单次单因子变量法OAT(one factor at a time),即选取仿真模型中的某输入变量,在其取值范围内改变数值,而保持其他变量不变,运行仿真模型即可得到系统预期产出的数值。可以用灵敏度系数Si表示资源投入变化(表1的流量、参数等变量)对预期产出变化(时间KPI)的影响,
(1)
其中P0为变量的初始值,Y0为模型的初始输出值,Pi为参数第i次运行值,Yi为模型第i次运行,经批均值法处理的仿真估计值(以下简称“输出值”)。本文每次仿真实验的4个输出值分别是YCT, i、YCTS, i、YDR, i、YMF, i。
根据S品牌的流程运营情况,把表1的变量初始值与仿真运行结果(时间KPI)代入式(1)进行局部灵敏度分析。结果表明,有7个变量的灵敏度系数较大,其他变量的灵敏度系数都较小。因此,优化产品开发流程时,应优先考虑这7个主要变量:服装设计速率(layout and design clothing)、制作面料花版(make fabric pattern)、面料生产速率(produce fabric)、款式面料比(clothing per fabric)、单款订货量(order amount per clothing)、服装款式(design clothing)、二样款式(second pattern clothing)。
2.2 流程时间的优化
结合影响流程的7个主要变量,可以制定各变量的具体优化方案,对产品开发流程进行仿真实验,改善流程运营的资源配置。流程内各变量的优化方案可分为两类:一类是增加投入流程资源,从而增加变量的数值,提升产品设计能力,加快交付周期,提高产品质量和价值,促进流程运营效率以及保证产品安全等;另一类是减少投入流程资源,从而减少变量的数值,降低运营成本和物料库存,减少各环节的等待时间,减少资源浪费等。其中,服装设计速率、制作面料花版、面料生产速率等3个变量随着资源投入的增大而增加,其他变量刚好相反。
本文把7个主要变量初值的资源投入设为基数100%,按照资源投入的比例增减进行分档仿真实验。Sterm认为,灵敏度分析的取值范围通常在统计或预测数值的2倍之内[5]。因此,本文的资源投入比例设为基数的25%到175%之间,增加资源投入分为3档:125%、150%、175%。减少资源投入亦分为3档:25%、50%、75%。这样,7个变量的仿真实验共有7×6=42组。
把变量运行值Pi、模型输出值Yi代入公式(1),可得每组仿真实验的灵敏度系数。为方便数据分析,对(Pi-P0)/P0进行绝对值处理,得到
(2)
此外,由于变量输入值与时间KPI的DR、MF正相关,而与时间KPI的CT、CTS负相关,故CT和CTS的灵敏度系数先取负值,然后再进行分析。经过处理后的7个主要变量的局部灵敏度系数,如表2所示。可以看到,处理后的灵敏度系数是正数时,资源投入对时间KPI有正影响;相反,灵敏度系数是负数,资源投入对时间KPI有负影响。
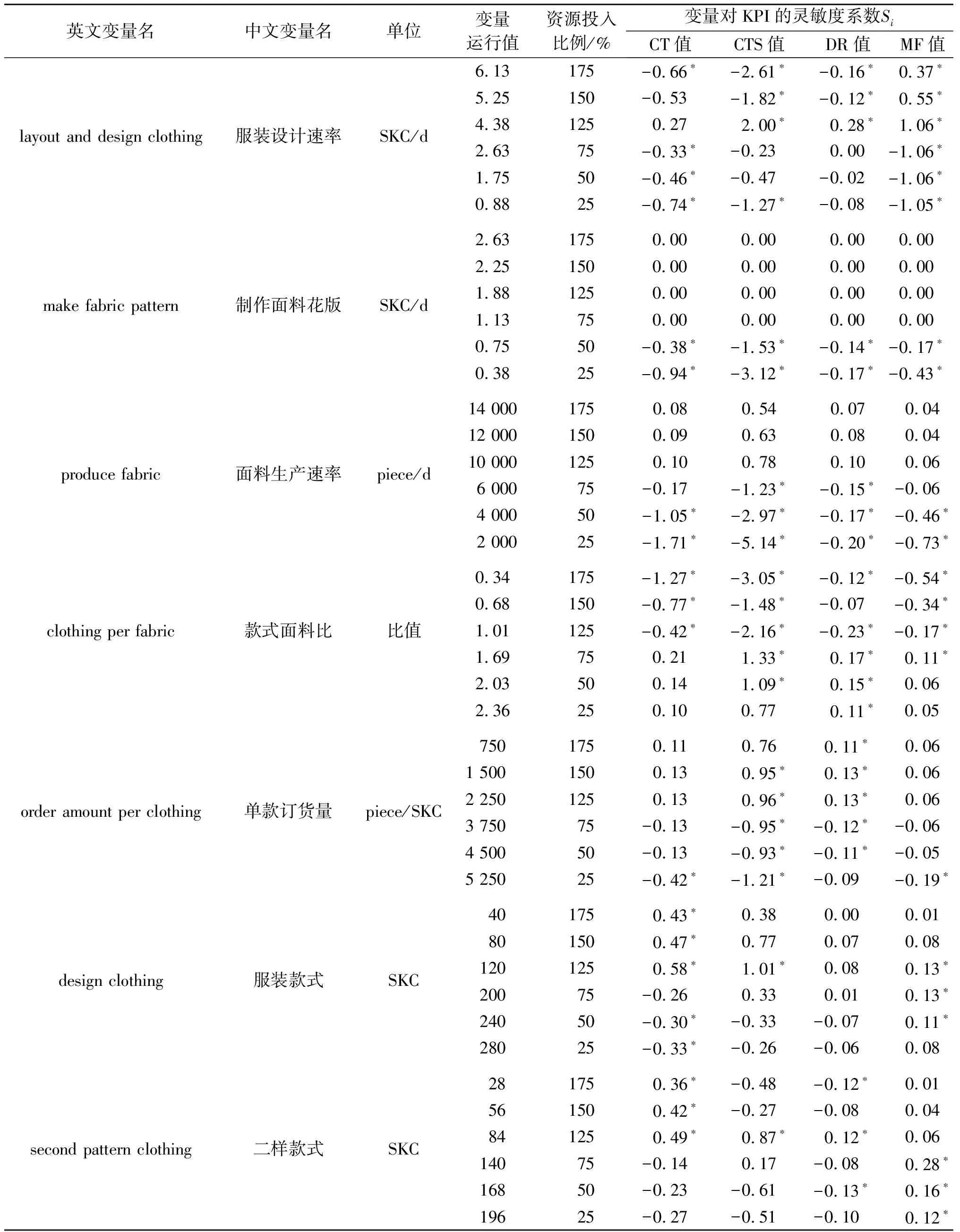
表2 时间KPI的局部灵敏度系数
3 分析与讨论
企业为形成并不断提高时间核心竞争力,需要根据内外部环境以及内部资源和能力,对投入资源进行总体规划,并选择合适的优化方案。以往制定流程优化策略时,多采用定性分析的方法。本文借鉴McKinsey矩阵(图2),对S品牌产品开发流程的优化方案进行分类,并统计分析各类优化方案的资源投入与预期效果(局部灵敏度系数)之间的关系,定量研究流程的优化策略问题,进而结合S品牌业务流程的实际运营状态,制定相应的优化策略,提高对现有流程的管控能力,扩大流程的增值空间[9]。
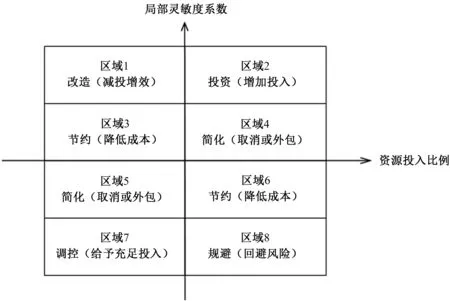
图2 优化策略的McKinsey矩阵Fig.2 McKinsey matrix for optimization strategies
首先,对优化方案的资源投入比例和局部灵敏度系数进行系统分类,每个优化方案都由资源投入及其预期效果进行综合评价。当投入比例>100%时,优化方案是高成本的,可增加该变量的投入;当投入比例≤100%时,优化方案是低成本的,可减少该变量的投入。而在评定优化方案的时间KPI时,往往希望灵敏度系数越大越好。本文根据KPI灵敏度系数的绝对值大小,将其分为高灵敏度和低灵敏度两类。由于进行了7×6=42组(168个)仿真实验,假设绝对值大小的排序百分比在前50%(即前21位)的优化方案是高灵敏的;反之,则是低灵敏的。以CT值为例,经计算得其灵敏度高低分界点为0.3。当CT值的灵敏度系数|Si|≥0.3时,优化方案是高灵敏的,对预期效果有较大影响;当CT值的灵敏度系数0≤|Si|<0.3时,优化方案是低灵敏的,对预期效果影响较小。同理,CTS值的灵敏度高低分界点为0.87;DR值的灵敏度高低分界点为0.11;MF值的灵敏度高低分界点为0.11。
其次,根据资源投入比例及其局部灵敏度系数的正负与高低,可将表2列出的优化方案划分为8个区域(图2)以及6类优化策略(改造、投资、节约、简化、调控、规避)。其中,区域3和6的优化策略均为“节约”,区域4和5的优化策略均为“简化”。以区域5的优化策略为例,减少资源投入比例,对有效产出的有负面影响,但不明显,灵敏度系数较低。此类变量用“简化”策略为宜:删除流程的不必要环节,减少成本的支出。对于企业来讲,这些环节花费了较多的人力、物力、财力,但并不能起到较大的作用。所以,要删除与实现流程目的关系不大、作用不大的环节,简化投入大、产出小的环节,还可以考虑采取合并或者外包的方法进行优化。
根据7个主要变量对6类优化策略的数量进行统计,得到表3。可知服装设计速率、款式面料比、单款订货量对时间KPI的影响较大,优化策略多数集中在改造、投资、调控、规避等灵敏度系数较高的区域,因而存在较大的风险。制作面料花版、面料生产速率的优化效果很小,然而这些变量如果投入不足,会转变为整个流程的阻碍,从而影响系统的有效产出。服装款式、二样款式等变量主要涉及产品开发流程的批量,有较大的优化空间,这两个变量落在调控、规避等区间的优化方案很少,风险较小。
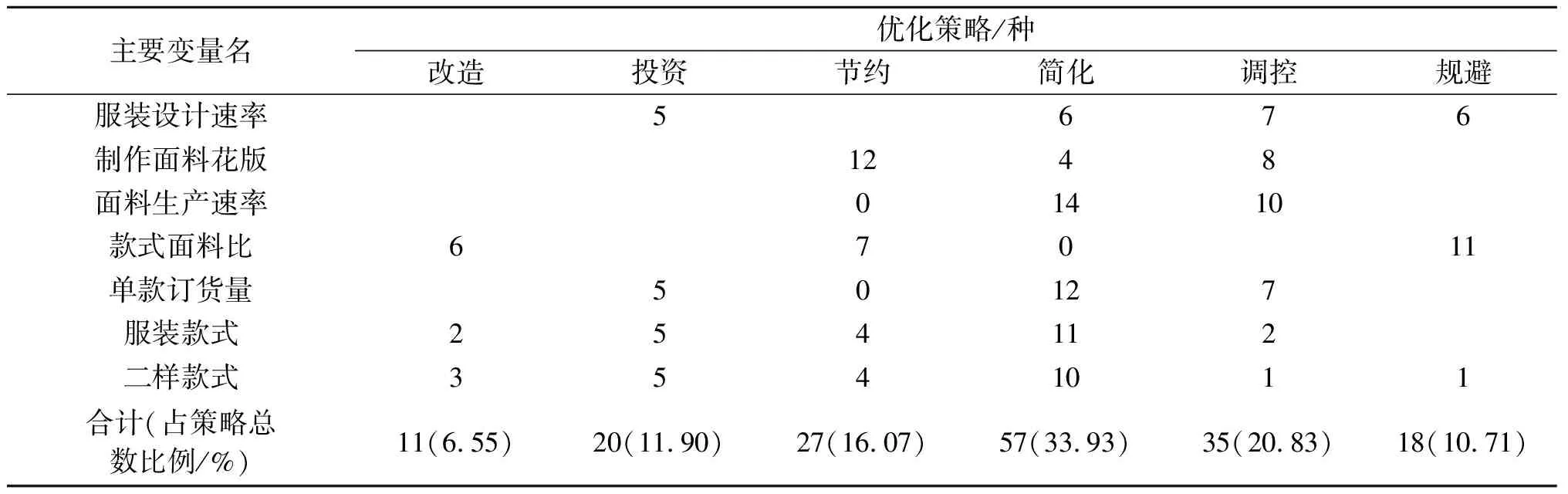
表3 各类优化策略的数量和比例(按主要变量统计)
根据4个时间KPI对6类优化策略的数量进行统计,得到表4。可以看到,采用改造、投资的高时效优化方案数量较少,占比18.45%;采用节约、简化等风险相对较小、能有效提高运营效率的优化方案数量较多,占比50%;需要及时调控和规避风险的优化方案占比31.55%。由此可见,不合理的参数优化比例是导致优化决策潜在风险的重要原因之一,应注意合理控制主要变量的优化比例,使其运行在合理的范围内,避免因过度优化对整个流程产生不稳定性和负影响。
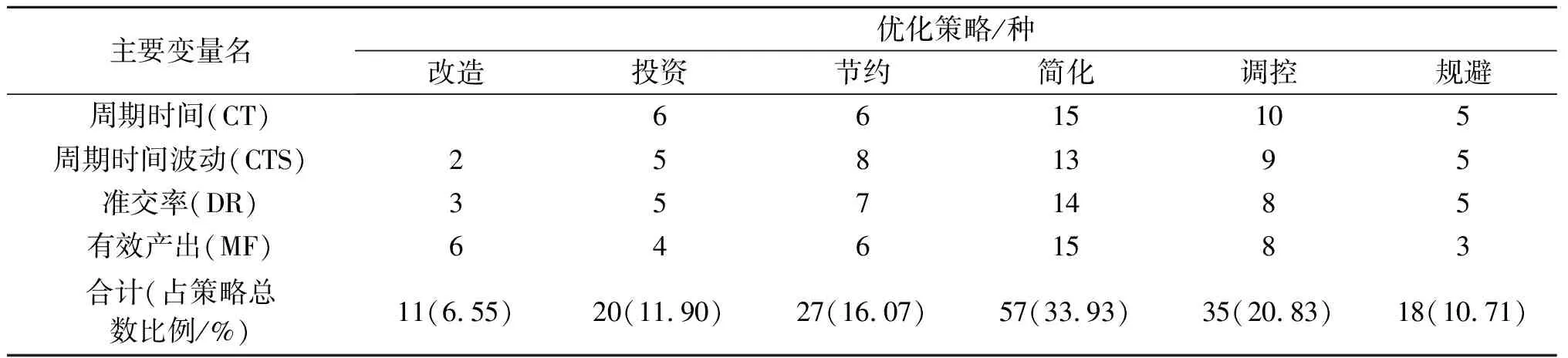
表4 各类优化策略的数量和比例(按时间KPI统计)
综上所述,优化方案的数量分布能较好地说明产品开发流程的特点以及流程的优化策略。作为一家经营状况良好的大型服装公司,S品牌的产品开发流程已相对比较完善。在不考虑进行大规模业务流程再造的情况下,选择节约、简化、调控等优化策略是比较稳妥和有效的。
4 小结
本文以S品牌的产品开发流程为实例,通过实地调研产品开发流程,建立了系统动力学模型,并进行数字化资源配置仿真实验,最后结合定性与定量分析,给出了流程的优化策略,主要结论如下。
1) 根据流程各变量参数的局部灵敏度系数大小,找到影响产品开发流程时效的7个主要变量——服装设计速率(layout and design clothing)、制作面料花版(make fabric pattern)、面料生产速率(produce fabric)、款式面料比(clothing per fabric)、单款订货量(order amount per clothing)、服装款式(design clothing)、二样款式(second pattern clothing);
2) 对各类优化方案进行数据分类、量化统计和比较,定量分析了主要变量的资源投入比例、预期效果、潜在风险等对产品开发流程的时效影响,为制定流程优化策略和方案提供了参考。
