基于排队论的机场出租车司机决策研究
——以郑州新郑国际机场为例
2023-11-01张二丽
张二丽, 黄 静, 刘 森
(1.郑州财经学院 统计与大数据学院,河南 郑州 450044; 2.郑州财经学院 中原统计研究所,河南 郑州 450044)
0 引言
机场出租车作为一种灵活的交通工具自然受到了广泛关注。郑州新郑国际机场的乘车区有两条并行车道,机场出租车管理人员负责“分批定量”放行出租车进入乘车区,同时安排一定数量的乘客上车。在保证车辆和乘客安全的条件下,如何设置最佳上车点,合理安排出租车与乘客,使总的乘车效率最高,是值得研究的问题。
1 模型假设及符号说明
假设:①乘客是无限排列的;②乘客排队的长度没有限制;③排队乘客默认为先到先上车;④在上车点排队的乘客自觉排成一列;⑤乘客上车时间符合负指数分布。本文使用的符号说明见表1。

表1 符号说明Tab.1 Symbol description
2 排队论
排队论系统由4部分组成:输入、输出、服务规则、服务设施。管理者能够通过排队系统合理均衡服务对象与服务设施之间的关系,从而使服务资源更加合理。在交通枢纽内的出租车上客区,通常会构建由乘客、空车作为输入,载客出租车作为输出以及出租车作为移动式“服务台”的出租车排队系统,以此实现枢纽内乘客高速离站的目的[1]。
2.1 单点式出租车排队系统
单点式,顾名思义,是只有一个上车点,所有乘客排成一列逐个上车的形式。系统内的乘客与出租车在各自的等待区排队等待,一辆出租车接客人,当此出租车出发后,下一辆出租车才能进入上车点载客。此类系统结构简单,适合客流量小的地域,对应的排队模型有MM1(MMS)排队模型[2](图1)。
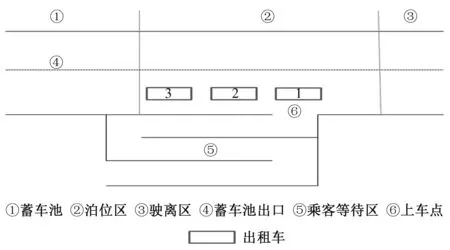
图1 单点出租车排队系统
2.2 多点纵列式出租车排队系统
多点纵列式较单点式多了n个上车点,使得乘客和出租车的等待时间大大缩减,提高了交通效率。虽然多点纵列式乘客也只有一条排队通道,但是却多了n-1个上车点,成功上车离开的乘客数增加,效率得以提升。但这种排队系统的纵向距离必须保证足够大,以确保多点式的顺利使用,常用于纵向距离足够大的地域(如图2,以n=3为例)。

图2 多点纵列式出租车排队系统
2.3 多点并列式出租车排队系统
多点并列式与多点纵列式相似却又不同,并列式的各个上车点并列排布,乘客排队结束后还需跨过出租车道到达上车点,这样安排虽提高了效率但安全性却降低了,在客流量大的情况下容易造成人车冲突,导致靠近乘客的车道上的出租车等待时间增长,因而影响整体效率。此类系统适用于上客区纵向较短横向较宽的地域(如图3所示,仍以3个上车点为例)。
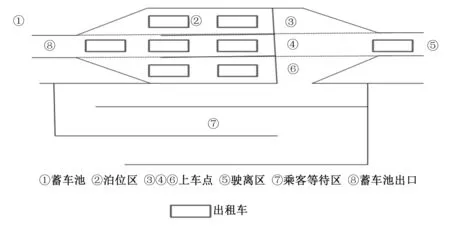
图3 多点并列式出租车排队系统
2.4 负指数分布
指数分布是参数λ的对称分布,记为Exp(λ),概率密度函数为
(1)
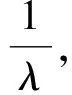
3 模型建立
在机场经常会遇到出租车排队载客和乘客排队乘车的情况。郑州新郑国际机场乘车区有两条并行车道,机场管理部门拟设置一个合适的上车点,考虑到出租车和乘客的安全问题,基于排队论系统建立排队论模型,从而合理安排出租车和乘客,使总的乘车效率最高。
3.1 多点并列(人行天桥)式出租车排队系统
已知出租车排队系统有3类,考虑从3种方案中选出最合适的。无论哪一类排队系统都是乘客排队等待出租车,同时出租车排队等待载人,然后驶离机场(如图4所示)。
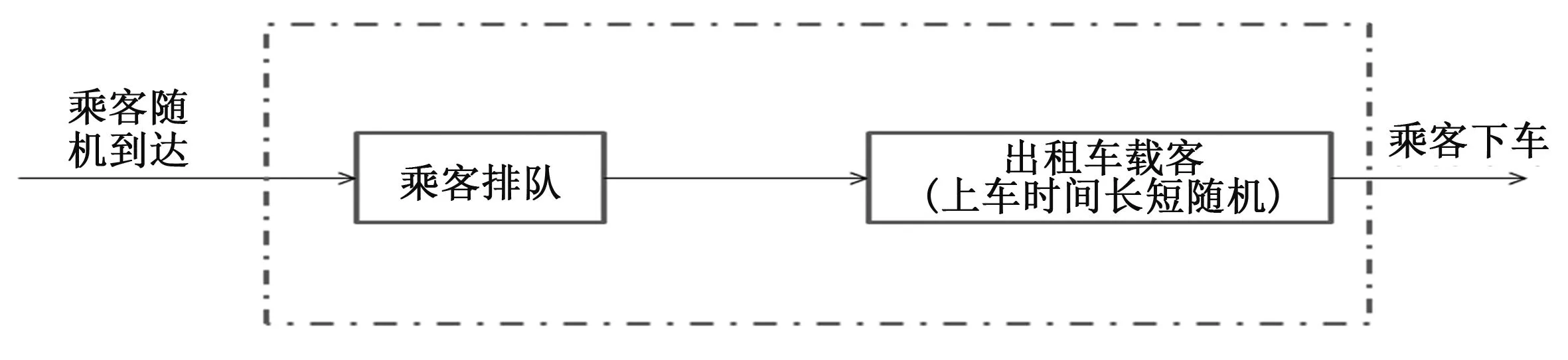
图4 排队系统
根据排队系统中乘客及出租车的状态,可以分为3个时期:忙期、闲期和休假期。繁忙率ρ表示排队系统的繁忙程度,是乘客到达率与多上车点排队系统中出租车司机的平均载人速率之比。ρ越大表示系统越繁忙,当ρ大于1时,系统处于无限排队繁忙状态[4],
(2)
在机场乘车区合理设置上车点。已知该机场乘车区有两条并行车道,要分析3类系统是否符合题意要求。
单点式出租车排队系统结构简单,可保证乘客和车辆的安全,但乘车效率低,因此不选择;多点纵列式出租车排队系统,能满足机场客流量大的问题,保证乘客排队上车时的安全,总效率也较高,但不能保证车辆进入和驶出上车点时的安全,故仍不选择;多点并列式出租车排队系统,适用于上客区纵向较短横向较宽的传统地域,不符合该机场的情况,在客流量大的情况下还容易造成人车冲突,会导致靠近乘客的车道上的出租车等待时间增长,从而影响出租车的整体效率,因此也不选用。
所以,3种传统系统都不适合,需考虑其他系统。就车辆安全而言,并列式最合适,现只需考虑怎样在保证乘客安全的情况下使总乘车效率最高。经分析,决定在并列式的基础上增加一座人行天桥以提升总乘车效率[5],且人行天桥可保证乘客安全(见图5)。
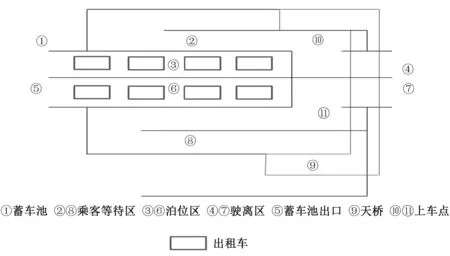
图5 多点并列(人行天桥)式出租车排队系统
3.2 多点并列(人行天桥)式出租车排队模型
根据排队论的相关知识,建立多点并列(人行天桥)式出租车排队系统的模型。若“上车点”排队系统完全处于忙期,且繁忙率ρ<1时,系统处于稳定状态而且不会形成无限排队的繁忙状态,基于此对系统的输入与输出建模。
在系统处于稳定状态时,C个上车点并联工作(此处C等于2),若系统中乘客数为n[6],则概率
(3)
(4)
若系统中乘客队长为L,等待时间为W,分析系统可得
(5)
(6)
3.3 模型优化
优化排队系统可选合适的费用决策模型。设乘客等待时的总费用为Z1=αL,建立“上车点”和人行天桥的费用为Z2=βC。α是每位乘客单位时间内等待时的费用,β是一个“上车点”乘客上车所用时间成本,若想得到最优系统,必须满足两者之和最小[7],此时有
minZ(C)=Z1+Z2=αLS(C)+βC,
(7)
(8)
即有
(9)
3.4 模型求解
根据郑州新郑国际机场出租车秩序管理部门实时观测得到的数据,单位时间内在两个上车点成功上车的乘客数约为4,单位时间内到达两个上车点的乘客数约为3,由此对郑州新郑国际机场出租车排队系统进行分析,通过Matlab计算单位时间内排队等待的平均人数,系统内的平均人数,平均逗留时间及平均等待时间,结果如表2所示。

表2 排队系统Tab.2 Queuing system
通过计算可得,当C=2时,满足公式(9),因此,当设置为两个“上车点”,可实现该排队系统费用较少。
4 结论
多点并列(人行天桥)式出租车排队模型在“乘车区”有两条并行车道的情况下,设置“上车点”,并横跨两条车道搭建人行天桥,缓解了并列式模型在客流量大的情况下造成人车冲突,靠近乘客车道上的出租车等待时间较长的弊端,提升了出租车整体载客效率,出租车司机的利益也更加有保障。多点并列(人行天桥)式出租车系统适合纵向较窄、横向较宽且客流量较大的地域环境。相比传统并列式模型而言,改善后的排队模型更适用,此模型可为郑州市新郑国际机场出租车管理部门提供参考。
