改进随机森林算法在用电预测中的应用
2023-11-01熊洁,牛燕,刘伟
熊 洁,牛 燕,刘 伟
(国网湖北省电力有限公司鄂州供电公司,湖北 鄂州 436000)
0 前言
随着“双碳”目标的逐步实施和新型电力系统的建设,推动用电革命、确保用电供应、推进能源转型已成为新的电力工作重点。准确预测地区全社会用电量对地方电力企业节能减排、合理安排产能消纳、实现“削峰平谷”等具有重要意义。用电数据是经济发展的“风向标”。准确预测地区全社会用电量对区域经济发展的评估具有一定作用。因此,用电预测模型的准确性和稳定性尤为重要。
近年来,用电量预测研究成果丰硕,针对不同应用场景、不同数据特征,适用的预测模型有所不同。康辉等[1]认为产业结构的变化是用电量波动的原因之一。因此,其在预测用电量的指标体系中,除高耗能行业外,增加了第一、第二产业增加值作为预测指标,并从绝对误差、模型震荡程度、适用性和经验值这4个方面评价预测结果的准确性。冯伟等[2]利用误差反向传播(back propagation,BP)神经网络,采集面积、国内生产总值、人口数量、大型企业数量、农机总动力、民营企业数量、建筑业总产值和公路里程这8个方面的影响因素,对泰州的月用电量进行预测。其提高了春节和7~8月用电高峰期的预测精度。学者们利用差分自回归整合滑动平均(auto regressive integrated moving average,ARIMA)模型在时间序列预测方面的优势,对不同地区的年用电量进行预测。该模型在短期内(1年)的预测效果较为理想[3-4]。吴文培[5]利用极限梯度提升机(extreme gradient boosting,XGBoost)对数据进行预测先验,并采用先验结果优化 Prophet 模型,以防止过拟合现象;同时,指出预测差异主要是温度升高引起的,因此建议下一步需增加气温数据以进行修正。毛锦伟等[6]利用聚类方法对用电数据进行分类,将自组织特征映射(self-organizing feature maps,SOM)神经网络和多变量的径向基函数(radial basis function,RBF)相结合搭建神经网络模型,采集国内生产总值、人口、固定资产投资等影响因素,以构建某省用电量预测模型。其比较了单一模型和混合模型的预测差异,指出了混合模型的优势。陈露东等[7]比较了ARIMA、卷积神经网络(convolutional neural networks,CNN)-长短期记忆(long short-term memory,LSTM)网络和生成对抗网络的预测(predict using generative adversarial network,PGAN)模型在日电量预测中的差异,指出PGAN模型存在精度高的优点,以及计算时间长的缺点。胡春凤等[8]从用电量、气象、交通、经济这4类共340个变量集中,采用弹性网络因子、Granger因果关系分析找出用电量的影响因素,并预测月用电量。其结果与向量自回归(vector auto regression,VAR)、BP、最小绝对值收缩和选择算子(least absolute shrinkage and selection operator,LASSO)模型相比,更加精准。曹敏等[9]为避免自回归滑动平均(auto regressive moving average,ARMA)模型对外生因素考虑不足的问题,引入支持向量机(support vector machine,SVM)模型。其对SVM模型加以修正,并对不同企业的年用电量进行预测,预测结果较单独使用ARMA和SVM模型更加准确。刘侃等[10]采用LSTM模型改进ARIMA模型,以LSTM预测用电量、ARIMA修正残差,对某园区企业周用电量进行预测,并比较了单一方法与组合方法的预测精度差异。李艳青[11]比较了多元线性回归、季节趋势、指数平滑这3种方法对钢铁企业的年用电量的预测结果,指出季节趋势结果适用于长期发展规律研究,而指数平滑则偏重于中短期预测。沈豫等[12]采用Granger因果关系提取与用电量预测有显著影响的产业经济指标,构建自回归分布滞后(auto regressive distributed lag,ARDL)方法用电量预测模型,对高耗能产业月用电量进行预测。预测结果准确性高于自回归(auto regressive,AR)模型。
上述研究大多数使用时间序列、机器学习或两者相结合的方式,对地区、行业或企业分年、月、日电量进行预测,均有一定参考意义。地区用电量是行业电量的线性组合,行业电量的发展趋势不尽相同,因此增加了地区用电量预测的不确定性。一方面,从历史地区用电量预测未来地区用电量,容易因各行业的不同发展趋势导致预测结果产生偏差。而从行业预测出发,合成地区预测用电量的研究还存在一定空白,是值得深入研究的细分领域。另一方面,时间序列的地区用电量属于非线性数据。ARIMA模型的缺点在于无法处理非线性数据。本文考虑到ARIMA模型的残差包含了非线性信息,可以采用ARIMA模型预测的残差来分析数据的非线性成分。因此,本文提出ARIMA和随机森林(random forest,RF)的混合模型——季节性自回归整合滑动平均-随机森林(seasonal auto regressive integrated moving average-random forest,SARIMA-RF)模型。该模型通过发挥ARIMA和RF的各自优势,在处理非线性数据的同时,得出较为准确的预测结果。
1 电力市场用电量预测相关理论模型
1.1 K-means聚类算法
作为聚类算法之一,K-means算法得到了广泛的运用。K-means算法主要思想如下:给定K个初始类簇中心点以及K值后,分配各数据到与其距离最近类簇中心点的类簇中;分配完全部点后,计算1个类簇中全部点的中心点 (一般采取平均值);以该点为中心点,再次重新分配点。如此迭代计算,对类簇中心点进行更新并循环往复,直到类簇中心点基本上没有变化,或满足预定要求的迭代次数。
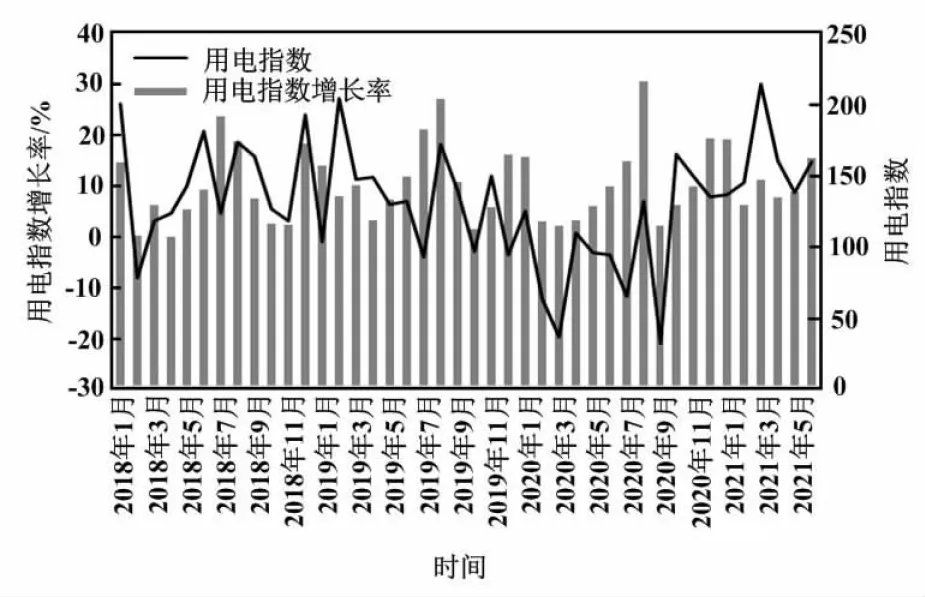
本文假设数据样本X涵盖了n个对象,即X={X1,X2,…,Xn},且各对象的属性均涵盖m个维度。对K-means算法而言,其目标是按照对象之间的相似性,将上述n个对象集聚在指定的k个类簇中,并使得每个对象到其所在类簇中心点的距离最小。K-means应对k个聚类中心{C1,C2,…,Ck}(1 (1) 式中:Xi为第i个对象(1≤i≤n);Cj为第j个聚类中心(1≤j≤k);Xit为第i个对象的第t个属性;Cjt为第j个聚类中心的第t个属性(1≤t≤m)。 本文分别对比各对象到各聚类中心之间的距离,并分配各对象到最近距离的聚类中心的类簇中,获得了k个类簇{S1,S2,…,Sk}。 K-means算法借助类簇中心,对类簇的原型进行界定。类簇中心即类簇内全部对象在诸多维度的平均值。其计算式如式(2)所示。 (2) 式中:Cl为第l个聚类的中心;当1≤l≤k时,SL、Xi分别为第l个类簇中对象的个数以及第i个对象(1≤i≤|SL|)。 第k个决策树能够生成θk(随机变量)。θk和前面生成的θ1,θ2,…,θk-1,θk相互独立,但概率分布相同。决策树借助训练集和θk实现了生长后,能够塑造出分类器h(x,θk)。x为输入的特征向量。其在生成了很多决策树后,借助投票的方式,选出理想方案。 RF是由很多分类树{h(x,θk),k=1,2,…,n}共同组合而成的分类器。随机变量{θk}呈现出独立同分布的特点。各分类树均参与到投票中,以决出最后的输出。 本文给定多个分类树h1(x),h2(x),…,hk(x),从随机向量X、Y的分布中随机挑选训练集。边缘函数的定义如式(3)所示。 (3) 式中:I[hk(X)=Y]为指示函数;j为X分类中的随机种类。 式(3)边缘函数用于测量平均正确分类数超过平均错误分类数的程度。边缘函数值越大,分类预测越可靠。 时间序列中的规则周期称为季节性(seasonal,S)。SARIMA作为ARIMA模型的拓展,被广泛应用于预测季节性时间序列。 SARIMA在ARIMA(p,d,q)的基础上增加了3个超参数(P,D,Q)和s,即SARIMA(p,d,q)(P,D,Q,s)。 其中:p为非季节性ARIMA的滑动窗口数;P为SARIMA的滑动窗口数;q为非季节性滑动平均(moving average,MA)滑动窗口数;Q为季节性MA滑动窗口数;d为非季节性差分阶数;D为季节性差分阶数;s为季节性周期参数。 某省用电量为非线性数据,SARIMA不能提取数据的非线性成分。SARIMA模型的缺点在于无法处理非线性数据。考虑到SARIMA模型的残差包含了非线性信息,可以利用SARIMA模型预测的残差分析数据的非线性成分。因此,本文提出SARIMA和机器学习方法的混合模型SARIMA-RF。 SARIMA-RF预测流程如图1所示。 图1 SARIMA-RF预测流程图Fig.1 SARIMA-RF prediction flowchart 为了提高预测效率、加快预测速度,需要对各行业的历史用电量数据进行聚类。K-means聚类算法简单、快速,可以有效地对行业用电量进行预测。本文在确定k值的前提下,快速划分类别,以提炼不同类别的用电差异和用电规律。在此基础上,本文采用RF算法对地区全社会用电量进行预测。 本文在进行K-means分类之前,需要对各行业用电量数据进行处理。处理方式如下。 ①对各行业用电量进行降序排列。 ②计算各行业用电量的累计百分比。 ③筛选累计百分比在99%以内的各行业。因累计百分比低于1%的部分行业用电量过小,不具有典型性,且在分类过程中处理困难,故本文只选取累计百分比在99%以内的各行业。 经处理,本文在71个行业中选出了59个行业,并利用K-means聚类算法对所选的58个行业用电量进行分类。 本文利用K-means聚类算法,对某省2018年1月至2021年6月的月度用电数据进行聚类,并将行业用电量分为了5类。为了便于统计和计算,本文采用指数的方式进行测算,分别对5类行业测算月均总用电指数、行业月均用电指数、月用电极差指数、用电变异系数等,以观察不同行业分类下的各类行业用电特点。 行业用电分类基本情况如表1所示。 表1 行业用电分类基本情况表Tab.1 Basic table of classification of electricity consumption by industry ①第1类行业月均总用电指数最高,达到137.9。其包含6个行业,分别是城镇居民、电力/热力的生产和供应业、黑色金属冶炼和压延加工业、化学原料和化学制品制造业、乡村居民和非金属矿物制品业。 第1类行业总用电指数及同比增长率如图2所示。 图2 第1类行业总用电指数及同比增长率Fig.2 Total electricity consumption index and year-on-year growth rate for category 1 industries 总用电指数具有一定的季节波动性。每年2月,行业用电量均有不同程度的回落。受2020年2月疫情的影响,3月总用电指数跌至低点,用电指数仅为112.1。行业总用电指数同比增速降低(仅为-20.4%),降幅超过20%。第1类行业受疫情影响用电指数具有一定滞后性。滞后期为1个月左右。2020年9月受发电企业用电负值的影响,用电指数降至112.0,同比增速降为21.7%。随着疫情得到有效控制,各行各业逐渐复工复产,第1类行业总用电指数迅速提升,2020年8月达到峰值214.0。2020年12月、2021年1月均保持较高的用电指数,分别为173.9、173.3,恢复势头迅猛。 ②第2类行业总用电指数不高,处于中等水平,为38.4。其包含6个行业,分别是有色金属冶炼和压延加工业、房地产业、计算机/通信和其他电子设备制造业、金属制品业、纺织业和汽车制造业。 第2类行业总用电指数及同比增长率如图3所示。 图3 第2类行业总用电指数及同比增长率Fig.3 Total electricity consumption index and year-on-year growth rate for category 2 industries 第2类行业总用电指数具有一定的季节波动性,2020年2月行业总用电指数较低。与第1类行业相比,第2类行业受疫情影响更大。2020年2月总用电指数急速下滑,仅为14.9,同比下降53.3%。2021年2月总用电指数急剧上升,同比增长率高达125.7%,较2020年增长1倍以上,略高于2019年2月的用电水平,即恢复到疫情前用电水平。除疫情引起的特殊波动外,不同月份的用电波动较小,月用电极差指数仅为36.8,用电变异系数为0.19。 ③第3类行业总用电量指数最低,仅为24.3。行业月均用电量略高(为3.5),仅高于第5类行业。其包含7个行业,分别是教育/文化/体育和娱乐业、铁路运输业、住宿和餐饮业、水利/环境和公共设施管理业、石油/煤炭及其他燃料加工业、电气机械和器材制造业、橡胶/塑料制品业。 第3类行业总用电指数及同比增长率如图4所示。 图4 第3类行业总用电指数及同比增长率Fig.4 Total electricity consumption index and year-on-year growth rate for category 3 industries 第3类行业的总用电指数具有一定的淡旺季特征。淡季集中在2~5月,2月并没有明显的走低现象。旺季集中在7~9月。受疫情影响,2020年2月总用电指数仅为12.6,同比下降49.0%。2021年2月增速达到97.0%。结合峰度、偏度等可以看出,第3类行业用电指数的走势与第2类行业较为相似。 ④第4类行业总用电指数相对较高,为66.4,但波动大,用电变异系数为0.37,是5类行业中波动最大的行业分类。其包含13个行业,分别是农副食品加工业、水生产和供应业、卫生和社会工作、造纸和纸制品业、公共管理和社会组织/国际组织、医药制造业、通用设备制造业、其他制造业、农/林/牧/渔服务业、道路运输业、建筑装饰/装修和其他建筑业、房屋建筑业、非金属矿采选业。 第4类行业总用电指数及同比增长率如图5所示。 图5 第4类行业总用电指数及同比增长率Fig.5 Total electricity consumption index and year-on-year growth rate for category 4 industries 第4类行业总用电指数具有明显的季节性,2月总用电指数下滑明显。2020年其用电指数受疫情影响并不严重,2020年2月总用电指数仅下滑12.1%,是5类行业中下滑最低的一类。但2020年9月同样出现发电企业负电量的现象,9月总用电指数仅为2.3,同比下降96.2%。第4类行业用电极差指数较大(为142.3,接近150),是5类行业中最大的一类,这说明该类行业月用电差异大。随着疫情影响逐渐消失,2020年第四季度开始,其总用电指数趋于稳定,仅有小幅波动。 ⑤第5类行业总用电指数偏低,行业月均用电指数最低,仅为1.0。这说明该类行业用电量较少,电力不是主要的生产资料,或者行业规模较小。该类行业包含行业最多,共26个,分别是电信/广播电视和卫星传输服务、农业、木材加工和木/竹/藤/棕/草制品业、食品制造业、铁路/船舶/航空航天和其他运输设备制造业、多式联运和运输代理业、科学研究和技术服务业、其他采矿业、畜牧业、黑色金属矿采选业、商务服务以及租赁业、土木工程建筑业、专用设备制造业、互联网以及相关服务、酒/饮料及精制茶制造业、纺织服装/服饰业、居民服务/修理和其他服务业、金融业、有色金属矿采选业、燃气生产和供应业、金属制品/机械和设备修理业、石油和天燃气开采业、废弃资源综合利用业、装卸搬运和仓储业、软件和信息技术服务业、化学纤维制造业。 第5类行业总用电指数及同比增长率如图6所示。 图6 第5类行业总用电指数及同比增长率Fig.6 Total electricity consumption index and year-on-year growth rate for category 5 industries 第5类行业总用电指数相对稳定,季节性较强,具有明显的周期性。除2020年2月、2021年2月因疫情导致总用电指数同比增长率异常波动外,其他月份均较为稳定,同比增长率基本控制在±20%以内。2020年疫情后用电有所复苏,行业总用电量指数从2020年2月的12.4上升到2020年9月的35.6,超过2019年同期水平。这说明疫情后用电量恢复情况较好。2020年第四季度到2021年上半年,总用电指数均保持同期较高水平。 5个类型行业的用电波动程度不同、疫情对行业用电影响不同、用电增长情况不同等,对用电量预测产生较大影响。如果将其叠加起来进行预测,预测结果难免出现较大偏差。因此,各行业需要各自选择合适的预测模型,以保证预测准确性。 本文针对K-means聚类所划分的5个不同梯度的行业用电量,分别采用SARIMA、RF、SARIMA-RF模型对不同类型的行业总用电指数进行预测,以预测2021年7~10月5类行业总用电指数。因用电行业并非全部行业,故由模型所算得的预测值需按比例调整,以确定全社会用电指数预测值。 2021年全社会用电指数真实值与预测值对比如表2所示。 表2 2021年全社会用电指数真实值与预测值对比表Tab.2 Comparison of real value and forecast value of the index of electricity consumption of whole society in 2021 由表2可知,SARIMA-RF模型预测偏差整体有所改善。2021年8~10月,某省全社会用电量呈现下降趋势。随着夏季高温天气的减少,“迎峰度夏”到达尾段,8~10月某省全社会用电量有下降趋势符合预期。 用电预测不仅关乎电力公司经营管理,而且关系着合理安排电力生产、提高用电保障、降低电力运维成本等,是电力企业经营规划中必不可少的数据基础。精准的数据预测可以协助电力公司预判未来潜在用电客户增长地区、行业分布等,以提升电网规划的科学性和电网投资的精准性、提高电网投资效益。同时,精准的用电预测可以配合政府制订、优化、调整分时电价、阶梯电价、差别电价等,支撑完善电力中长期交易、现货市场交易机制,以防范电价政策调整风险。 本文选取某省代表性行业58个,利用K-means聚类方法将58个行业用电数据分为5类。5类行业的用电趋势各不相同。本文根据每一类型行业的用电特点,采用SARIMA和RF混合模型分别预测出各类型行业的用电指数。本文合成全社会用电量的预测值,以观察用电发展趋势。经检验,本文模型具有较好的稳定性,预测结果最大相对误差控制在2.0%以内。 由于各地区产业结构具有较大差异,导致用电结构同样存在一定差异,不同地区的用电预测模型不尽相同。针对不同地区的经济特点,应采取与之相适应的预测模型,并按照实际情况对不同的预测模型加以完善。1.2 RF算法
1.3 SARIMA
1.4 SARIMA-RF

2 行业用电量分类
2.1 数据预处理
2.2 K-means聚类划分行业用电类型





3 全社会用电指数预测

4 结论
