板状结构非线性超声导波理论与成像方法研究进展

赵成威,李 健,陈世利,刘 洋,项延训,邓明晰,曾周末

(1.天津大学精密测试技术及仪器全国重点实验室,天津 300072;2.华东理工大学机械工程与动力工程学院,上海 200237;3.重庆大学航空航天学院,重庆 400044)

0 引言

随着无损检测(nondestructive examination,NDE)和结构健康监测(structural health monitoring,SHM)技术的快速发展,超声导波技术已在核电、氢能储运、石油化工、测井勘探、航空航天等众多工程领域引起了广泛关注[1-2]。然而,对于以氢损伤、微裂纹、位错滑移、晶相析出等为代表的早期材料损伤的检测,传统线性超声导波因检出极限过高会导致服役构件维护成本上升[1,3],甚至会因维护不及时而引发灾难性后果。

非线性超声导波技术对材料疲劳损伤十分敏感,可在微观结构演化阶段检测到声场变化,从而有效增加结构状态的管理域[1,3]。该技术能够基于晶格原子间的非线性力学相互作用,利用谐波幅度上的微小变化反推材料微观结构演变,对以氢损伤、微裂纹、位错滑移、晶相析出等为代表的早期材料损伤的检测具有独特优势[1]。然而,非线性理论较为复杂,并且在实际工况中激励累积非线性导波十分困难。这给非线性领域研究人员带来困扰。

本文对非线性超声导波技术的研究现状与发展历程进行综述,介绍非线性超声导波在波导中的产生和传播机理,并探讨非线性超声导波应用在层析成像技术中的潜力,旨在为NDE和SHM领域的研究人员提供参考。

1 非线性超声导波的研究进展

非线性超声导波在结构生命周期管理中具有巨大潜力。结构损伤萌生曲线如图1所示。

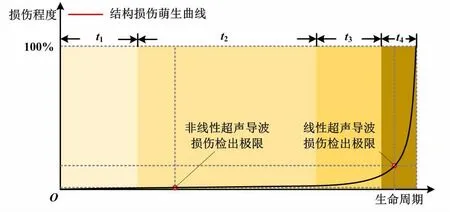
图1 结构损伤萌生曲线Fig.1 Structural damage emergence curve

图1中:t1～t4分别代表初始损伤产生、微观结构演化、微损伤连接和宏观缺陷生长的时间。由图1可知,隐蔽性较强的早期损伤萌生占据了生命周期的大部分时间[1,3]。非线性超声导波可在疲劳损伤演变早期有效检测。自20世纪60年代以来,国内外学者在非线性超声对早期损伤微观形态的敏感机理和特性方面开展了大量研究。早期研究集中在发掘弹性非线性和结构位错对体波的影响。美国中西部研究所的Taylor等[4]和Jones等[5]通过对弹性波相互作用微分方程进行分析,提出了纵波混频概念,对激励混频谐波的内部共振条件进行了总结,为体波混频方法理论奠定了基础。同为美国中西部研究所的Rollins从理论层面分析了弹性波在均匀连续固体介质中的传播特性,推导出弹性能展开式中三阶项的非线性解[6]。布朗大学的Hikata等通过一系列单晶铝和合金铝试验对固体中非线性体波谐波理论模型进行了验证[7-9]。

1.1 板中非线性超声导波理论发展

近年来,非线性超声导波逐渐成为新的研究热点,并广泛用于板材、管道、钢轨等结构的微缺陷和早期损伤检测。板中非线性超声导波理论发展示例如图2所示。

图2 板中非线性超声导波理论发展示例Fig.2 Example of the development of nonlinear ultrasonic guided wave theory in plate

重庆大学的邓明晰采用部分波法和界面反射法,率先解释了板材中导波累积二次谐波与混频谐波效应,提出了具有累积效应的非线性导波解析式,并对谐波波场的对称性质进行了总结[10-12]。图2证明了水平剪切波激励是累积的兰姆波二次谐波。德克萨斯大学奥斯汀分校的Hamilton和de Lima研究了兰姆波在各向同性自由边界板中的传播特性,列出了激励和差谐波所需要满足的内部共振条件,从而科学阐释了任意截面波导中二次谐波的产生和传播过程,为非线性导波激励的频率选择和应用提供了理论指导[13-14]。加州大学圣地亚哥分校的di Scalea等[15-16]和佐治亚理工学院的Müller等[17]均从各向同性板材中兰姆波二次谐波激励入手,研究了谐波与波运动对称性质的关系,并总结了谐波共振非零能量流方程与相速度/群速度的匹配条件。宾夕法尼亚州立大学的Rose、Lissenden和Liu等详细分析了在均质各向同性板中激励累积二次谐波的选择条件[18];将应变能方程展开至第三阶,提出了1种分析各向同性弱非线性弹性板中导波模式相互作用的广义方法,对三次谐波在非线性板中的累积效应展开了深入研究;探讨了在谐波产生过程中水平剪切波和兰姆波之间的转换关系[19-21]。华东理工大学的赵成威等[22]和北京工业大学的何存富等[23]均研究了非共线混频超声检测方法,实现了材料塑性损伤和闭合裂纹的定位与表征。广西大学的毛汉领等提出了基于共线波混频技术的组合非线性超声参数预测模型[24]。上海交通大学的申岩峰等建立了用于模拟兰姆波产生、传播、波裂线性和非线性相互作用以及接收的二维分析框架,并将时间反转技术扩展到非线性兰姆波领域[25]。

1.2 非线性超声与结构损伤耦合机理研究

材料微观结构的特征控制着结构所表现的宏观性质。因此,要深入研究非线性导波的产生与传播特性,必须掌握声波在波导中与微观结构的耦合机理[26]。非线性超声与结构损伤耦合机理研究示例如图3所示。

图3 非线性超声与结构损伤耦合机理研究示例Fig.3 Example of study on coupling mechanism between nonlinear ultrasound and structural damage

美国国家航空航天局的Cantrell等提出了1种多晶固体中声谐波与共格应变的关系模型[27],采用材料非线性参数β量化波畸变,证明了材料中位错亚结构的存在[28]。此外,Cantrell还对微扰超声波作用下的解析模型建立进行了深入研究[29]。邓明晰等从理论层面证明了累积二次谐波及混频谐波对波导结构局部微小变化存在敏感性[30-31]。斯坦福大学的Cash等利用位错动力学模拟方法,定量预测了准静态载荷下滑移面的声学非线性参数[32]。华东理工大学的轩福贞等从晶格层面开展了二次谐波对材料蠕变敏感性的研究,证明了如图3所示的非线性效应会随着合金析出率和位错密度的增加而增加[33]。釜山大学的Cho等探索了导波非线性系数与材料热疲劳加载之间的关系[34]。何存富等开展了结构损伤混频检测机理及信号特征提取方法的理论研究,并通过共线混频结构微裂纹检测技术的研究,证明了异侧激励混频检测模式能够检测和定位结构中的微裂纹[35]。Lissenden等利用仿真建模证明了材料退化与产生高次谐波/混频谐波的相关性[36]。

1.3 非线性超声导波试验研究进展

激励非线性导波的初始条件极为苛刻,且易受到系统非线性的影响,是非线性导波检测技术在NDE领域开展产业化应用亟待攻克的业界难题[37]。因此,国内外学者在非线性导波试验研究方面也作出了大量的贡献。非线性超声导波试验研究进展示例如图4所示。

图4 非线性超声导波试验研究进展示例Fig.4 Examples of experimental research advances in nonlinear ultrasonic guided wave

佐治亚理工学院的Jacobs等采用压电换能器来追踪镍基高温合金的疲劳损伤演化,表明了非线性参数β可用于材料寿命预测[38]。邓明晰等在航空铝板[39]和P92钢板[40]分别进行了非线性导波试验系统的建立,利用兰姆波二次谐波准确评价了材料疲劳损伤。Lissenden等采用了聚偏二氟乙烯(Polyvinylidene difluorine,PVDF)换能器激励水平剪切波,利用其产生的兰姆波二次谐波对铝板疲劳损伤进行了表征,证明了谐波与基频波的振幅比具有不受仪器非线性影响的能力[41]。何存富等将二次谐波的弹性迟滞和耗散迟滞非线性系数应用于炉管结垢状况的检测[42]。项延训等设计了PVDF压电薄膜梳状换能器,成功激励了累积二次谐波[43]。南昌航空大学的陈振华等利用疲劳拉伸机制备了5005铝合金板材试件,并验证了利用兰姆波二次谐波检测板材微裂纹的实用性[44]。武汉工程大学的陈汉新等从试验层面研究了裂纹缺陷的出现和深度变化对导波非线性效应的影响[45]。

导波具有多模式特性。波导表面传播会产生频散效应。一方面,非线性导波可以像线性导波一样,利用波结构分析选择一定模式和频率的组合,优化谐波对缺陷的敏感性,并通过控制外界干扰实现导波在目标位置的聚焦。另一方面,累积的谐波具有更广的传播范围。所以,有必要对非线性超声导波理论进行深究,对用于激励累积谐波的基频模式进行高效筛选。这将有益于非线性导波检测技术在NDE、SHM和材料测定等领域的广泛应用。

2 非线性波动理论

邓明晰等通过结合微扰摄动理论与非线性反射法,发展了超声导波的二次谐波、三次谐波和混频谐波理论[10-12]。Rose在多位学者的研究基础上,归纳了固体中的超声导波理论模型,详细阐述了波在板、杆、空心圆柱体、多层介质等不同结构中的传播特性[37]。本文仅展示兰姆波二次谐波的经典理论推导过程,通过连续介质力学的应力-应变分析来解决板状各向同性波导结构中导波传播的边界条件问题。非线性导波的场方程是在笛卡尔坐标系中利用格林-拉格朗日应变张量E建立的[18]。E的表达式为:

(1)

式中:H为位移矢量的梯度;u为x1轴方向的位移梯度。

Murnaghan模型能够准确描述超弹性材料的声弹性和动态非线性弹性,并能够利用Landau-Lifshitz超弹性本构模型三阶弹性常数(third-order elastic constants,TOECs)中A、B和C与Murnaghan模型TOECs中v1、v2和v3(或另一种表达,即l、m和n)的直接关系。三阶应变能函数W可表示为[46-48]:

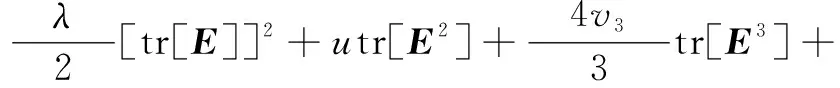
(2)

式中:tr为求张量迹的符号;λ和u为拉梅常数。

式(2)中包含了三阶项,能准确描述二次谐波的产生[3]。为了分析高次谐波,必须保留等式中的高阶项。

第二Piola-Kirchhoff应力张量T2为:

(3)

式中:I为单位张量。

(4)

式中:L1为u1对应的线性应力场;ρ为密度;S为板材表面的应力张量;nx3为与板平面垂直的单位矢量。

二次谐波控制方程为:

(5)

式中:L2为u2对应的线性应力场;NL(1,1)的基本形式为NL(m,n),代表基频模式m和n因相互作用产生的非线性应力场,而二次谐波属于m=n时的自作用情况,因此采用上角标NL(1,1)表示。

针对二次谐波场,u2可通过导波模式展开并简化为[37]:

(6)

式中:Am(x1)为二次谐波正交模式m″的幅值,um为m的位移分量,可用于描述波结构;ω为角频率。

Am(x1)是本小节所研究的关键参数。只有当Am(x1)≠0时,才会产生累积谐波。Lissenden表示二次谐波场,是通过施加正交模式展开来确定的[3],而正交关系的确定可以参考Auld所提出的互易关系[49]:

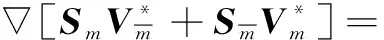
(7)

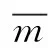
因此,依据模式正交关系,可以将波导中平均能量流Pmn表示为:

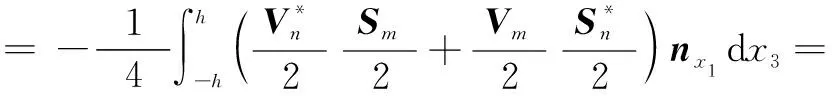
(8)

式中:h为板厚的一半。

若视二次谐波场2ω为式(7)的特殊情况[3],那么求解Am(x1)需要采用S、V和F重新表达式(6)中的位移分量:

(9)

式中:Re为求实部的符号。

式(7)引入到二次波场,可改写为:

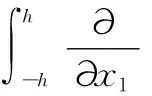
(10)

将正交和非正交模式的波场表达式代入式(10),可推导出常微分方程:

m∈Z+

(11)

式中:fns和fnv分别为通过表面和体积将能量流从基频兰姆波传递到谐波的非线性驱动力;Z+为正整数。

(12)

利用积分的方法求解式(11),可推导出:

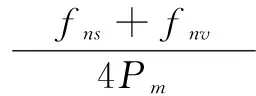
(13)

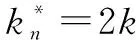
3 板中非线性导波的产生

3.1 相位匹配

当基频兰姆波与二次谐波具有相同的cp时,会使二次谐波与基波以零相位差向前传播。目前,学者们通常采用图形化的方法在频散曲线中寻找相位匹配点[3,18]。Lissenden等[19]和di Scalea等[15-16]已经证明了非零能量流耦合只发生在对称兰姆波二次谐波上,因此只需要考虑二次谐波对称模式(S模式)的频散关系。

为了满足相位匹配条件,二次谐波必须满足基频兰姆波S模式的原始频散关系:

(14)

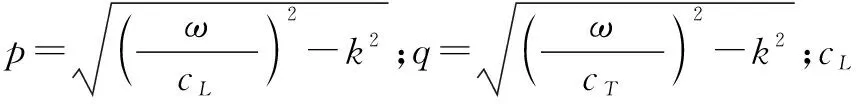
根据三角函数关系,式(14)可以被改写为:

sin(ph)sin(qh)[cos(2ph)-cos(2qh)]=0

(15)

式(15)可以有3个不同的解,分别为qh=nπ、ph=nπ和qh±ph=nπ。通过这3个解可以推导出激励对称R-L模式兰姆波二次谐波的5个条件[3]。

①k=0。此时代表截止频率。但该处的基频兰姆波有cp→∞,且二次谐波属于驻波,并不会传播。

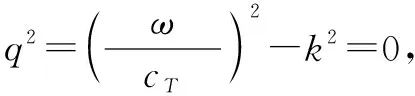
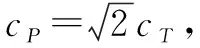
(3)当qh±ph=nπ时,存在tan(qh)=tan(ph)。该等式表达了另一种特殊情况,即发生在S模式和A模式(波结构的反对称模式)的频散曲线交叉点。

3.2 非零能量流

非零能量流是二次谐波产生共振的能量来源。Hamilton等[13-14]、di Scalea等[15-16]和Lissenden等[3]已经分析了波结构的对称性和反对称性。表1列出了兰姆波的速度、位移和位移梯度场和能量流的对称特性。

表1 兰姆波的速度、位移、位移梯度场和能量流的对称性Tab.1 Symmetry of velocity,displacement,displacement gradient and power flux in Lamb waves

表1中:S′代表波结构的对称方程;A′代表波结构反对称方程。此外,表1还包括将位移与位移梯度场代入·SNL(1,1)和SNL(1,1)中所得到的对称特性[13-19]。

表1所示的波结构对称特性,可以直接用于推断二次谐波的模式能量流是否存在。

(16)

将表1中的变量代入式(16),可以求得S模式和A模式的fns为:

(17)

同理,S模式和A模式的非线性体积能量流fnv为:

(18)

因此,式(17)和式(18)验证了板材中兰姆波或水平剪切波所产生的累积二次谐波均为S模式的兰姆波这一理论。

通过上述相位匹配条件和非零能量流耦合的详细分析,与板材表面导波模式和频率相关的二次谐波内部共振点可以从理论层面确定。通过图形化方法,在频散曲线中标注了如图5所示的用于激励累积增长二次谐波的5个模式对[48]。

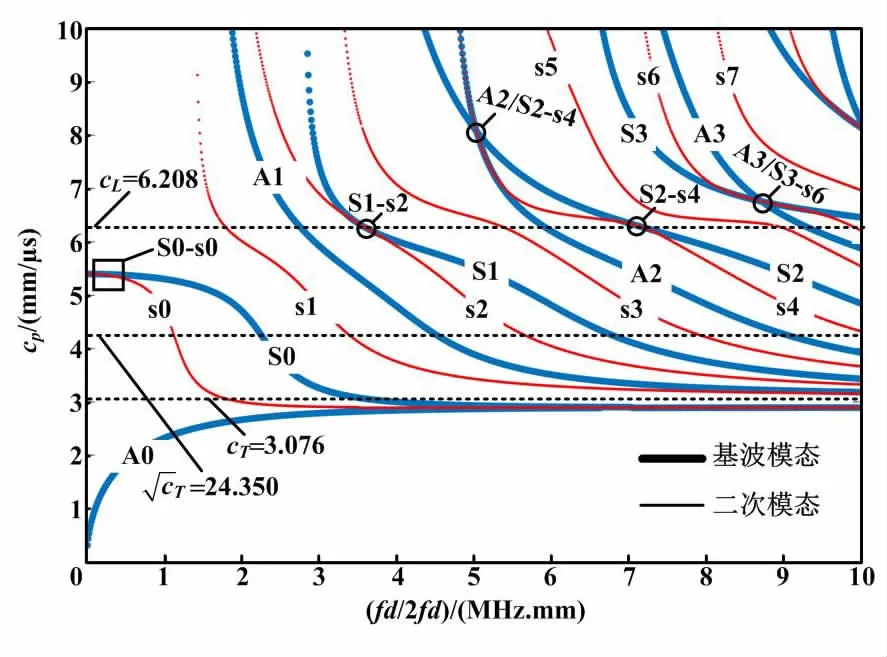
图5 用于激励累积增长二次谐波的5个模式对Fig.5 Five mode pairs for excitation of cumulative growth second harmonics

①S1-s2模式对是激励谐波的常用模式对[50,52,55],与S2-s4模式对均属于cp=cL时的情况。Lissenden等已经分析了这2处模式对的基频兰姆波与二次谐波除相位匹配外还具有相等的群速度值。群速度匹配作为附加条件,可使能量流传递效率大幅提高[18]。佐治亚理工学院的Kim等从试验角度论证了群速度匹配对能量流传递效率的积极作用[56]。Jacobs等通过试验证明了S1-s2模式对是该试验最优选择,并表明了S2-s4模式对具有对材料非线性的强敏感性[57]。

除上述内部共振点之外,Fan等通过试验证明了在低频范围内的S0模式同样具有激励累积二次谐波s0模式的能力[52],并且Liu等也表明了该模式对激励二次谐波及三次谐波的适用性[48]。如图5中的黑色方形标记所示,S0-s0模式对虽然属于有空间周期性的有界振荡,但在如fd<1 MHz.mm这种低频范围内,该模式对能激励出累积二次谐波。由于二次谐波幅值与波数平方成正比[3],S0-s0模式对会存在因谐波共振能量流有限而易受到外界系统非线性干扰的问题。

值得一提的是,Rose对源影响的分析表明了内部共振点的区域大小依赖于激励信号的频率带宽和与换能器尺寸相关的cp带宽[37],因此图5中的5个标记点均在一定区域内有效。

4 超声导波层析成像方法

4.1 典型超声导波层析成像方法

非线性超声导波虽可大幅度改善材料结构系统的生命周期管理,但在激励与接收换能器之间,其仅能在传播路径所覆盖区域内进行声场监测,而难以在该区域内准确且高效地定位诱发非线性响应的早期损伤位置[58]。近年来,国内外学者开始将层析成像方法应用于超声导波检测领域[37]。该方法将具有激励和接收位移功能的换能器组成一定规模的阵列,并在阵列内进行大物理域声场监测,而无需再逐一检测传播路径中的每个点。在NDE领域,典型的超声导波层析成像方法主要分为3类,分别为射线层析成像、衍射层析成像和全波形反演成像。

射线层析成像方法忽略波的折射和衍射,仅考虑以直线的形式传播,采用导波信号中的飞行时间、幅值、信号差异系数等作为变量进行重构。该方法适用于重构较大且平滑变化的缺陷,最小可分辨尺寸通常由第一菲涅耳区来描述[59-62]。衍射层析成像方法通常基于线性化散射场近似模型(如Born或Rytov近似),适用于重构相位畸变较低且对比度较低的缺陷。该方法的分辨率高于射线层析成像[63-66]。全波形反演成像方法起初应用在地震波成像领域[67-68],2016年被Fan等用于腐蚀金属板剩余厚度的精确重构[69]。该方法利用数值正演模型预测导波通过腐蚀缺陷时所产生的散射,并采用迭代逆模型重构腐蚀剖面。超声导波层析成像的代表性研究进展如表2所示。

4.2 非线性超声导波层析成像方法

上述典型超声导波层析成像方法采用的特征参量均源于线性导波,包括走时、幅值、信号差异系数、相速度、群速度等。因为没有利用非线性导波参数,所以检测的缺陷均属于宏观缺陷。尽管如此,超声导波层析成像一直在向着更高精度、更快速度、在线监测方向不断发展。最近,部分国内外学者开始专注于将非线性超声和阵列相结合以检测金属材料早期损伤的研究。Cho等通过分析非线性导波技术的发展,展望了非线性导波层析成像方法在NDE和SHM领域开展应用的潜力[72],研究了基于兰姆波的非线性超声导波层析成像方法。巴斯大学的Meo等发展了1种针对各向同性损伤结构动力响应的非线性超声导波层析成像方法。该方法使用双相干参数描述检测信号中由结构缺陷引起的二阶非线性特征,并通过与传统超声成像方法的对比证明了将非线性超声导波与层析成像方法结合的优势[73]。Meo等还采用稀疏压电陶瓷换能器阵列和二阶非线性超声对复合材料板中的冲击损伤进行了定位,将兰姆波的二倍频与基频的幅值之比的极大值点确定为冲击点。此方法在200 mm范围内的定位误差为4～22 mm[74]。南京邮电大学的王强等将二阶相对非线性参数变化率作为射线层析成像方法的特征参数,实现了6061铝合板材料疲劳损伤的定位和疲劳程度的表征[75]。

为充分证实非线性超声导波层析成像对材料早期检测的潜力与优势,本文举例介绍几项非线性层析成像研究并进行讨论。厦门大学与釜山大学的合作研究团队利用试验频域声场中的非线性表面波,实现了铝板微腐蚀缺陷图像的重构[76]。这项研究在尺寸为500 mm×500 mm×10 mm的铝板表面布置了由32个换能器组成的矩形阵列,利用大功率音脉冲系统产生中心频率为1 MHz的窄带信号作为激励源,并检测由氢腐蚀所引发的微坑或微裂纹。

在这项研究中,Cho等证明了传统线性损伤概率检测重构算法(reconstruction algorithm for probabilistic inspection of damage,RAPID)难以在检测区域内显示出任何含有微腐蚀损伤的信息。

代表性非线性层析成像结果如图6所示。

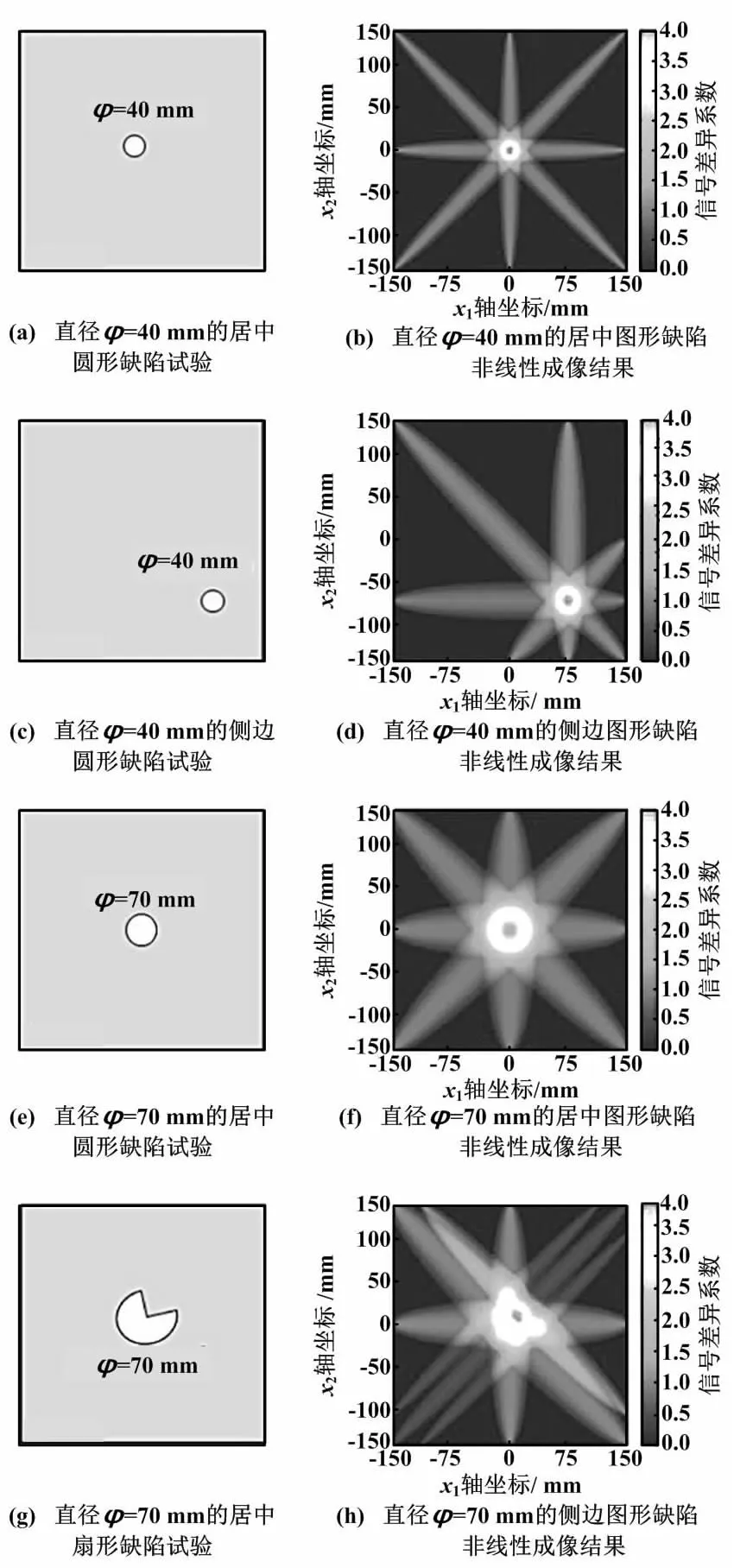
图6 代表性非线性层析成像结果Fig.6 Representative nonlinear tomography results

图6表明,由于微腐蚀缺陷的存在,频域声场中的二倍频处已产生明显的非线性响应。利用二倍频能量流变化的RAPID,可以将具有不同微腐蚀损伤试件中的声场失真转变为缺陷的可视化形式。

通常情况下,二倍频振幅比基频振幅小2个数量级,这意味着二次谐波往往会在声场中被忽视。重庆大学团队与厦门大学团队采用反相方法抵消了基频波,从而提高了累积二次谐波的信噪比[77]。

反相方法实现了二倍频在频域声场中的主导作用,显著提高了RAPID对微缺陷的成像分辨率。这项研究在尺寸为350 mm×350 mm×1 mm的铝板表面加工了尺寸约为20 mm×0.5 mm×0.2 mm的缺陷,并布置了由16个换能器组成的环形阵列;使用RAM 5000 SNAP超声波系统输出频率为0.6 MHz、循环为15个周期的正弦频响,通过衰减器进行信号降噪;以斜入射方式进行激励。

文献[77]的代表性非线性层析成像结果如图7所示。如图7(a)所示,采用反相方法可以有效抵消0.6 MHz处的基频峰,同时放大1.2 MHz处的二倍频峰至原来的2倍,使其在频谱中占据主导地位。

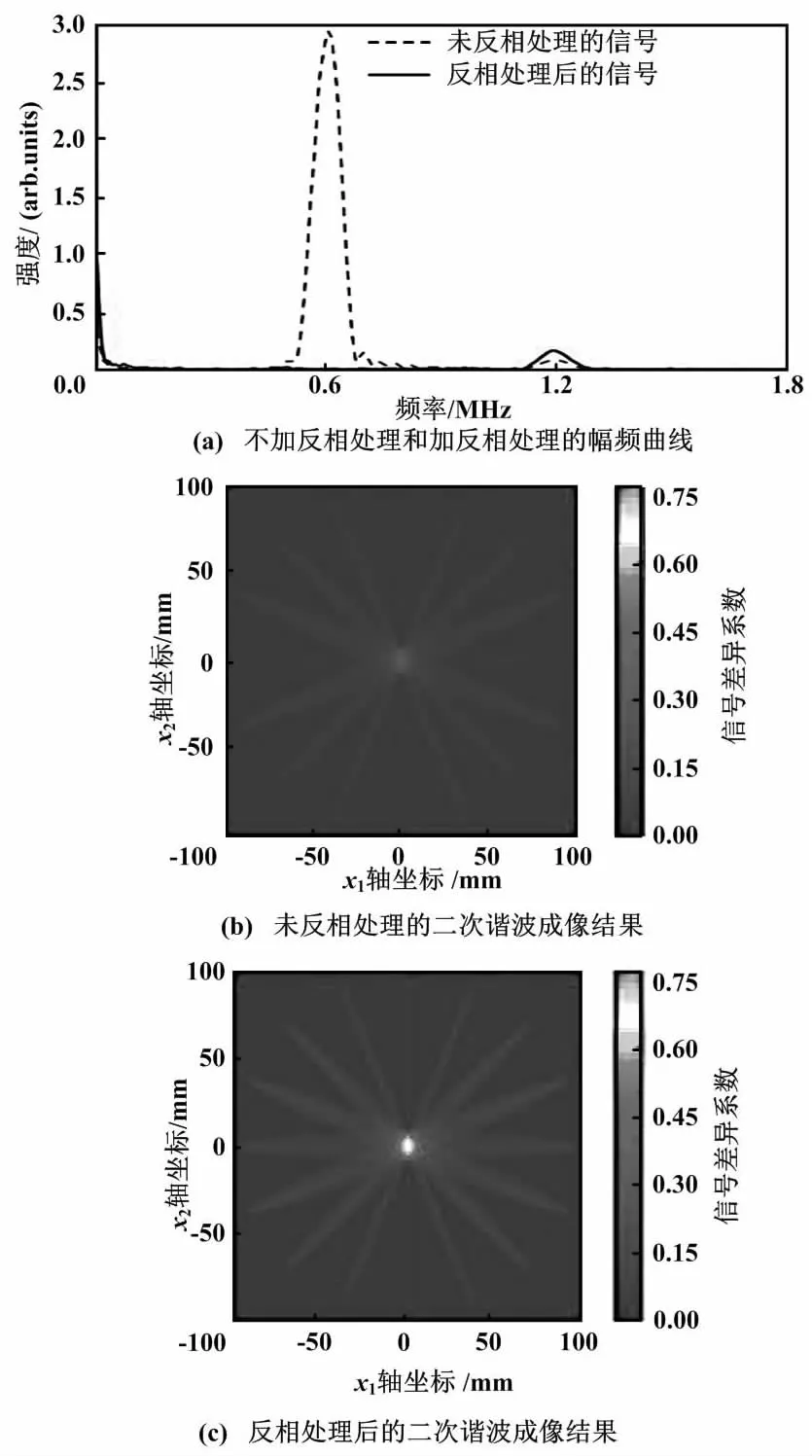
图7 文献[77]的代表性非线性层析成像结果Fig.7 Representative nonlinear tomography results from literature[77]

需要说明的是,由于兰姆波的频散特性,反相方法在本质上需要满足基频模式与二次谐波模式之间的相位匹配条件。图7(b)与7(c)的对比表明,在相同的成像可视化范围内(信号差异系数为0～0.75),基于反相方法的RAPID结果成像分辨率要明显优于传统提取二次频的RAPID成像分辨率。此外,虽然阵列仅由较为稀疏的16个换能器组成,但反相方法的应用有效改善了换能器数量和位置对成像质量的影响,间接地提高了RAPID的计算效率。

根据检测时换能器阵列中同时激励位移信号阵元数量的不同,阵列激励方式可分为串行激励和并行激励模式。虽然在线性导波领域,这2种激励模式的声场响应和成像结果完全相同,但在非线性领域2种激励模式会由于聚焦处的非线性响应与能量流损失的较大差别,从而导致非线性声场传播特性完全不同[78]。北京工业大学的研究团队通过对传感器阵列接收延时进行参数优化,成功实现了非线性阵列成像方法在微裂纹检测方面的应用[78]。这项研究在尺寸为240 mm×48 mm×25 mm的钢块表面放置了阵列探头,用于检测总长约29 mm的开口裂纹和闭合裂纹,并利用幅值为200 V、脉冲宽度为80 ns和中心频率为5 MHz的矩形脉冲信号,在采样率为25 MHz/s的条件下分别施加串行激励和并行激励。

在不同接收延时tr条件下,文献[75]的代表性非线性层析成像结果如图8所示。

图8 文献[75]的代表性非线性层析成像结果Fig.8 Representative nonlinear tomography imaging results from literature[75]

图8中:串行激励声动能Es和并行激励声动能Ep分布图的单位采用与信号差异相关的量纲单位,而通过Es-Ep获得的非线性成像结果的单位为dB。由成像结果可知,Es与Ep均随着tr的增加而减小。这是因为声场能量流随着传播时间增加而逐渐衰减。当tr=0.35 ms时,由于2种激励模式的声动能差异较小,非线性成像几乎无法准确反映裂纹的信息。当tr=0.67 ms时,非线性成像结果中可测得长度为29 mm的裂纹,与实际长度基本吻合。当tr=0.83 ms时,虽然非线性成像仍然能保持对裂纹表征的有效分辨率,但过大的时延会导致声场信噪比降低,从而使得成像结果中的缺陷范围明显增大。

文献[48]的代表性非线性层析成像结果如图9所示。

图9 文献[48]的代表性非线性层析成像结果Fig.9 Representative nonlinear tomography imaging results from literature[48]

材料蠕变产生的退化要比微裂纹具有更强的隐蔽性。关于采用非线性超声导波层析成像方法实现金属板材退化的可视化检测,天津大学的研究团队已经详细研究其理论模型与数值结果[48]。

由图9(a)可知,沿用图5对应的铝板材料参数,在由64个换能器组成的半径为400 mm的传感器阵列中,本文设置3个半径r和深度d相同但TOECs不同的圆形退化。其中,TOECs倍数的高/低代表退化的重/轻程度[79-80]。在这项研究中,Liu等证明了利用波衰减、波峰值和信号差异系数作为特征参量的线性超声导波层析成像方法几乎无法用于材料早期评价的层析成像方法之中[3,81-82]。基于非线性导波理论,该研究在ABAQUS VUMAT子程序中实现了Murnaghan超弹性本构关系,建立了广义非线性声学框架。该框架直接描述了Murnaghan材料应力场与弹性常数之间的关系。为有效限制高频段导波多模式干扰,其选用了如图5所示的S0-s0模式对激励累积二次谐波。不同程度退化的成像结果如图9(b)～图9(c)所示。其中,黑色虚线代表退化的实际位置。虽然RAPID会导致退化重构位置产生轻微的向心偏移[81],但其相对准确的重构结果足以体现二次谐波用于表征板材不同程度退化的潜力。此外,3个退化的信号差异峰值与退化程度呈现出标准的线性关系,表明非线性导波层析成像方法具有定量表征退化程度的潜力。

5 展望

尽管国内外学者已经通过理论和试验充分证实了利用非线性超声导波及其层析成像技术定性表征结构早期损伤的可行性和优势,但在实际工程应用方面仍有问题亟待解决。

①目前常用的基于整数倍高次谐波的非线性超声导波检测极易受到外界系统非线性的干扰。这些干扰包括检测系统的非线性、换能器的非线性、耦合剂的非线性,都属于非线性噪声的来源,很可能会导致对谐波来源的误判。

②非线性导波所利用的层析成像方法通常存在成像速度与重构精度不可兼得的问题,具体为:射线层析成像忽略了许多声场信息,从而难以实现材料早期损伤的定量化检测;衍射层析成像尽管成像分辨率有所提高,但距实现高分辨率定量化成像仍有一定距离;全波形反演成像由于海森矩阵计算的时间成本过高,严重影响了其在SHM领域的适用性。

面对这些挑战,本文认为发展任意阶和差谐波理论将是非线性超声导波方法的发展趋势[83-84]。该方法可借助非线性导波混频方法来消除系统非线性的影响,从而提高检测灵敏度。此外,为提升损伤区域的非线性力学本构方程的精确性,本文认为未来可以借助晶体塑性有限元法[85-86],通过精密微观形态观测和跨尺度数值计算[87-88],发展声导波精准混频理论与非线性导波散射声场理论[89-90]。该理论有望实现材料早期损伤微观形态和非线性导波可测特性的精确定量关联。另外,发展多参融合的射线层析成像方法可以提高重构分辨率,利用全部高次谐波与和差谐波的时域信号、频域信号、时频分析信号计算特征参数的信号差异系数。其中,特征参数包括但不限于走时、速度差异、幅值、反射系数、衰减、相位偏移、谐波幅度比等。同时,利用精确非线性力学本构方程可获得对实际导波波形的产生/传播具有更强描述能力的数学物理模型,从而可发展非线性导波全波形反演成像方法[91-92]。在此基础上,通过深度学习方法离线训练代替数据残差的在线迭代修正,结合有效避开局部极小值并加快收敛速度的方法,可以进一步提高材料早期损伤定量化检测成像速度[71,93-94]。

综上所述,非线性超声导波及其层析成像技术经过国内外学者多年来的潜心钻研,已在NDE和SHM领域占据重要地位。可以预见,非线性超声导波层析成像方法在未来将进入从定性表征向定量检测的跨越发展。其融合非线性超声导波与损伤微观结构演变耦合规律、精准非线性超声导波混频机理等,实现非线性超声导波检测定量化成像技术在实际工程方面的广泛应用,并为核电、氢能储运、石油化工、测井勘探、航空航天等众多工程领域结构健康监测提供技术支持。

6 结论

本文梳理了非线性超声导波与层析成像方法的代表性文献,总结了非线性超声导波在理论、耦合机理和试验方面的研究进展,推导了非线性波动理论、基频兰姆波与谐波的相位匹配和非零能量流耦合基础式;同时,本文概述了层析成像技术的分类,介绍了非线性超声导波层析成像方法的发展与应用,并对未来研究方向作出了展望。通过本文的综述可知,非线性超声导波可对改善SHM和结构生命周期管理提供强有力的NDE技术。具有累积效应的导波谐波不仅对微裂纹、位错、晶相析出等材料的早期损伤敏感,还可以传播相对较长的距离。此外,本文还介绍了结合层析成像的非线性超声导波方法。该方法能实现在阵列大物理域内微腐蚀、微裂纹和疲劳等早期损伤的定位和损伤程度的表征,从而大幅度提高成像分辨率。