家用自动洗碗机自由卫星喷臂设计研究

张婧宜 杜光辉 赵 通 李 翔 熊好平

（佛山市顺德区美的洗涤电器制造有限公司 佛山 528311）

引言

目前市面上洗碗机大多采用一字型单转喷臂，如图1 所示，喷孔洗涤轨迹为若干个同心圆，这些轨迹为喷孔直接喷射位置，而同心圆之间的区域，需要依靠水流的溅射、反射来清洗。相比传统单转喷臂，卫星喷臂的主副喷臂绕不同轴旋转，通过喷孔布局以及选取合适的转速比等，可加密轨迹、使喷射角度更加多样化，有利于减少洗涤死区。

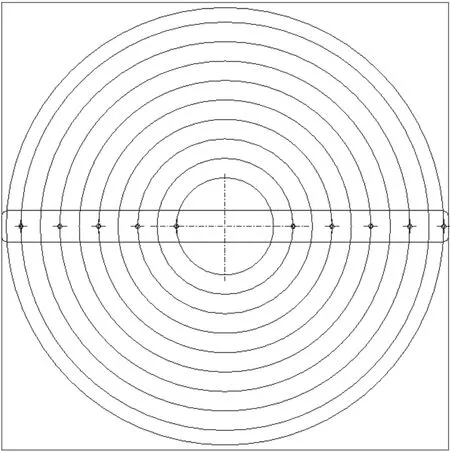
图1 传统单转喷臂洗涤轨迹

国内外洗碗机厂商对卫星喷臂的设计进行了大量研究，目前主要分为两个方向：一种是引入行星轮机构的卫星喷臂设计，如惠而浦采用了双副喷臂系统，其中一侧为齿轮传动，齿轮传动比为2 ∶1， 喷孔走对角线椭圆轨迹，可以更好的覆盖洗涤区域四角[1]；BEKO 采用特殊传动比4 ∶3，使喷孔走方形轨迹，减少四角洗涤死区[2]；美的45 机齿轮喷臂，利用双侧齿轮传动，使喷孔轨迹更匹配长方形洗涤区域等[3]。另一种方向为无齿轮传动系统的自由卫星喷臂设计，如AEG、伊莱克斯等卫星喷臂技术。本文将重点放在自由卫星喷臂的研究设计。

1 自由卫星喷臂主喷臂运动方式

无齿轮传动的自由旋转卫星喷臂，通过对主喷臂以及副喷臂上驱动孔的调整，可呈现两种运动方式。

1.1 主喷臂旋转呈现明显的周期性运动或“摇摆式”转动

如图2 所示，自由旋转的卫星喷臂系统，主喷臂在转动过程中，除了受主喷臂上驱动孔反冲力产生的转矩影响，同时副喷臂上驱动孔反冲力也会对主喷臂产生一个力矩，且随着副喷臂的转动周期性变化。当副喷臂对主喷臂产生的力矩接近或者大于主喷臂喷孔产生的驱动力矩时，主喷臂会呈现出明显的周期性转速变化或者“摇摆式”转动现象，比如AEG、伊莱克斯等卫星喷臂便是采用了该种运动方式。这种主喷臂“摇摆式转动”的方案优势在于增加副喷臂喷孔轨迹的复杂性，加密喷射轨迹，避开无齿轮卫星喷臂在某些特定的转速比下可能出现的较为稀疏的轨迹。

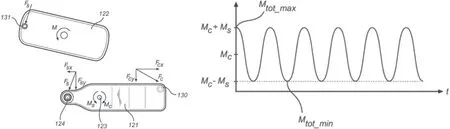
图2 伊莱克斯卫星喷臂转矩示意图[4]

1.2 主喷臂接近匀速转动

另一种情况是主喷臂接近匀速转动，假使副喷臂驱动孔对副喷臂产生的XY 平面方向的分力如图3 所示，根据力的平移定理，将这几个分力平移至副喷臂转轴位置，如果XY 平面方向的合力为零时，或者合力较小，则副喷臂驱动孔的反冲力对主喷臂的力矩远小于主喷臂驱动孔产生的力矩，此时副喷臂的转动对主喷臂转动产生的影响较小，主喷臂接近匀速转动，该转动状态可通过驱动孔的设计实现。但是采用该方案需特别注意，当主副喷臂均接近匀速转动时，某些特定的转速比下，可能出现较为稀疏的轨迹，背离了我们想利用卫星喷臂来加密喷射轨迹的初衷。因此，我们可以通过选择主副喷臂的旋转方向、转速比范围以及副喷臂的形态，比如双臂或者多臂来降低出现稀疏轨迹的风险。

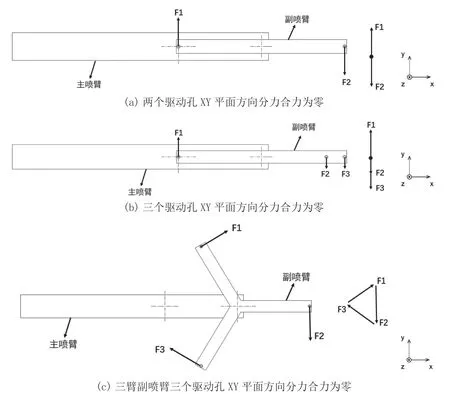
图3 副喷臂驱动孔XY 平面方向分力合力为零的几种情况

2 卫星喷臂副喷臂喷孔轨迹探究

以下将重点研究主副喷臂接近匀速转动时旋转方向、不同转速比、以及不同副喷臂形态对喷孔轨迹的影响。

2.1 主副喷臂同向转动时洗涤孔数量和转速比对喷孔轨迹的影响

2.1.1 单洗涤喷孔

如图4 所示，当主喷臂接近匀速转动且主副喷臂同向转动时，此时副喷臂上喷孔A 的轨迹满足外摆线参数方程：

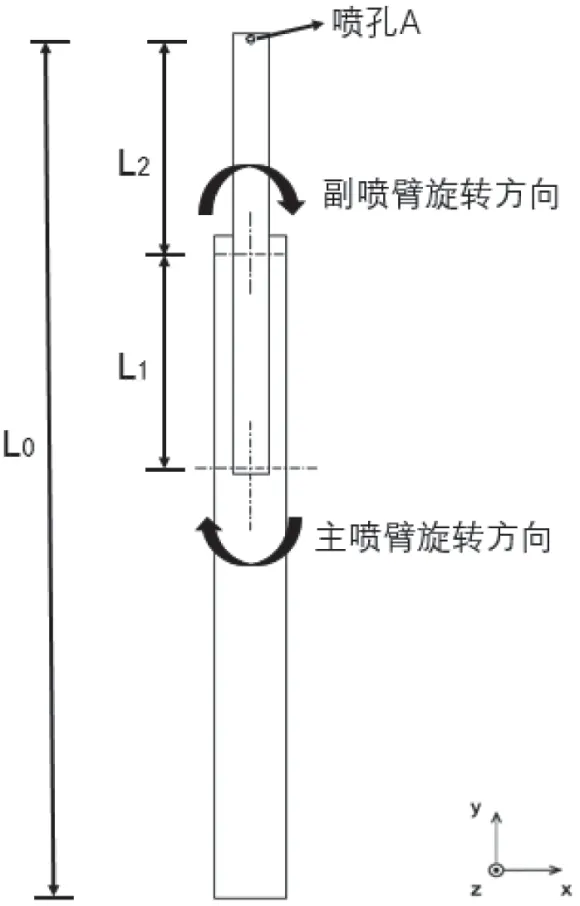
图4 单洗涤喷孔示意图

式中：

XA、YA—喷孔A 的横纵坐标；

θ—主喷臂转过的角度；

L1—主喷臂转轴距副喷臂转轴距离；

L2—副喷臂上喷孔距副喷臂转轴距离；

K—副喷臂与主喷臂转速比，取K=M/N，且M 与N互质。

假设洗涤区域为L0*L0的正方形区域， 取L1=L2=0.25*L0。

取不同转速比K 时，喷孔A 对应的轨迹曲线如下（正方形区域边长为L0）。

如图5 所示有如下规律，见图5（a）～（e），当K为整数时，K 越大，副喷臂喷孔A 轨迹越密集。当K 为有理数时，K=M/N，M+N 值越大，副喷臂喷孔A 走过的轨迹更加密集（M+N 相等时，K 值越大轨迹越密）。

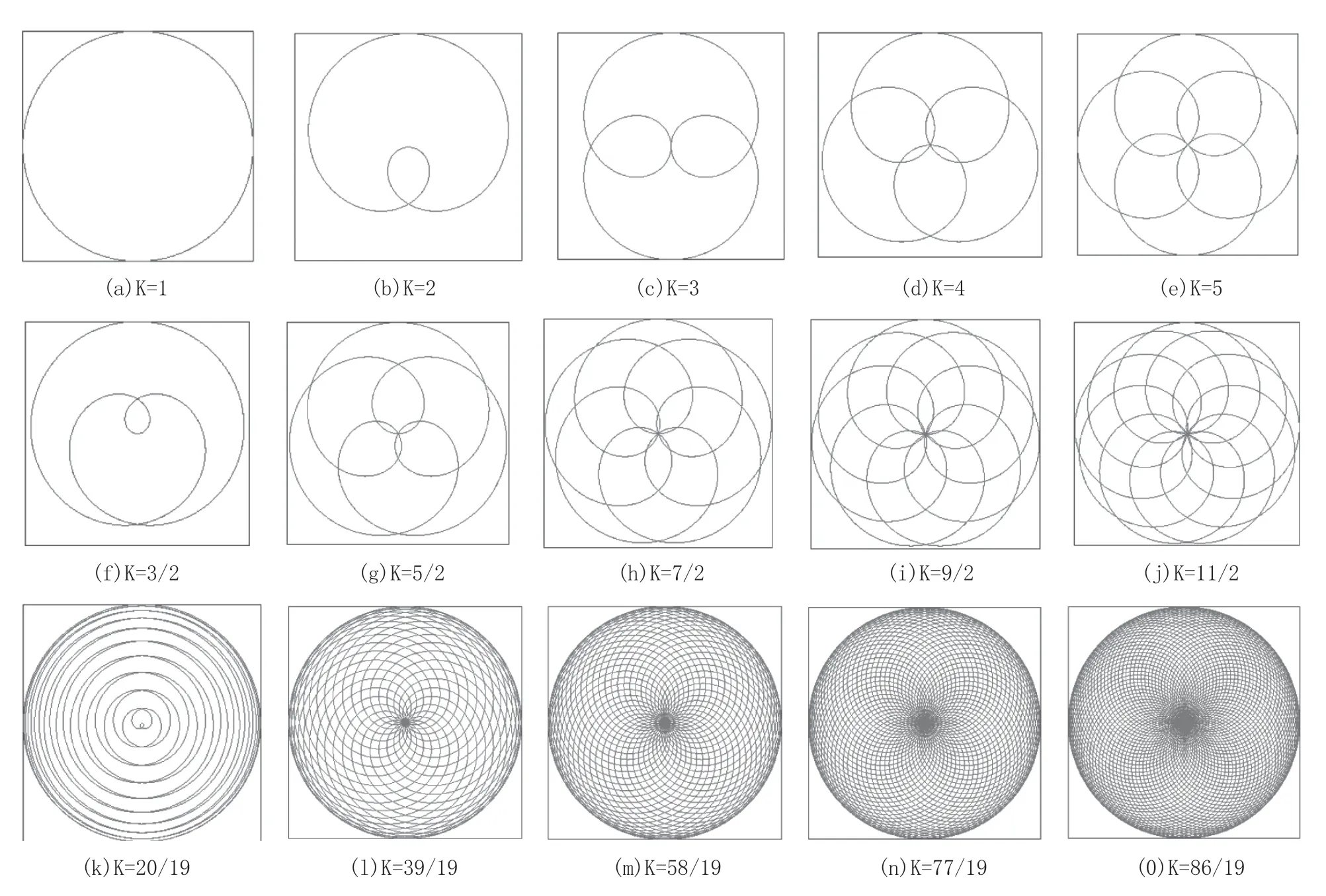
图5 喷孔A 轨迹曲线

在实际应用过程中，由于主副喷臂均为自由转动，无齿轮连接，因此无法确定具体的转速比，但是可以通过主副喷臂驱动孔的设计调整来确定主副喷臂的转速比范围。当在副喷臂上仅设置单个洗涤孔A 时（不包括副喷臂驱动孔），可取转速比K 大于4，这样即便出现最差的轨迹图（e），相比单转喷臂的圆形轨迹，单个喷孔走过的路径大大加长，到达的喷射位置更多，已经具备轨迹优势。

2.1.2 双洗涤喷孔

如图6 所示，当在副喷臂上设置两个洗涤喷孔时，需叠加喷孔B 的轨迹图如图7（灰色为喷孔A 的轨迹，黑色为喷孔B 轨迹）。

值得注意的是，当在副喷臂双侧设置喷孔A 和B 时，虽然对k=2、3、4、5 有加密喷射轨迹的作用，但当K取3/2、5/2、7/2、9/2、11/2 时，两个喷孔轨迹是重叠的，无加密喷射轨迹的作用。此时，推荐转速比为K 大于2.5，则可能出现的最差轨迹为图7（c），而该轨迹相比单转喷臂两个喷孔走的两个同心圆轨迹相比，已经具备优势。

2.1.3 三臂三洗涤喷孔

如图8 所示，当副喷臂形态为3 臂时，设置三个洗涤喷孔，此时喷孔轨迹图如图9（灰色曲线为喷孔A轨迹，浅灰色曲线为喷孔B 轨迹，黑色曲线为喷孔C轨迹）。

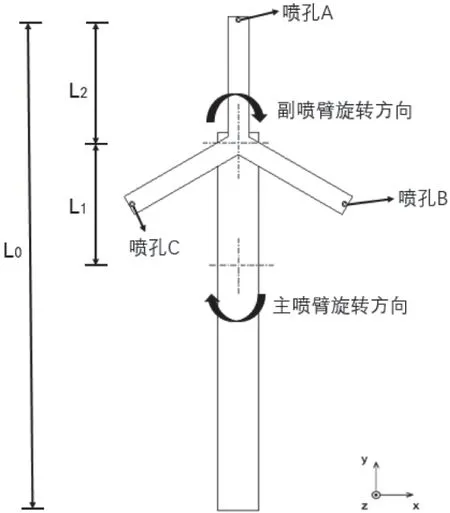
图8 三洗涤喷孔示意图

注意，当副喷臂形态为3 臂，夹角为120 °，且在其上设置3 个洗涤喷孔A、B、C 时，虽然对k=2、3、4、5、5/2、7/2、9/2、11/2 等轨迹有加密作用，但对K 取M/N，N=3 时，三个喷孔轨迹是重叠的，此时无加密轨迹的作用。推荐转速比范围取K 大于2，当K=7/3 时，即图9（i）为可能出现的最稀疏的轨迹，但此时三个喷孔的轨迹也比单转喷臂上的三个同心圆轨迹更具优势。

2.2 主副喷臂反向转动时洗涤孔数量和转速比对喷孔轨迹的影响

2.2.1 单洗涤喷孔

如图10 所示，当主喷臂接近匀速转动且主副喷臂反向转动时，此时副喷臂上喷孔A 的轨迹满足内摆线参数方程：

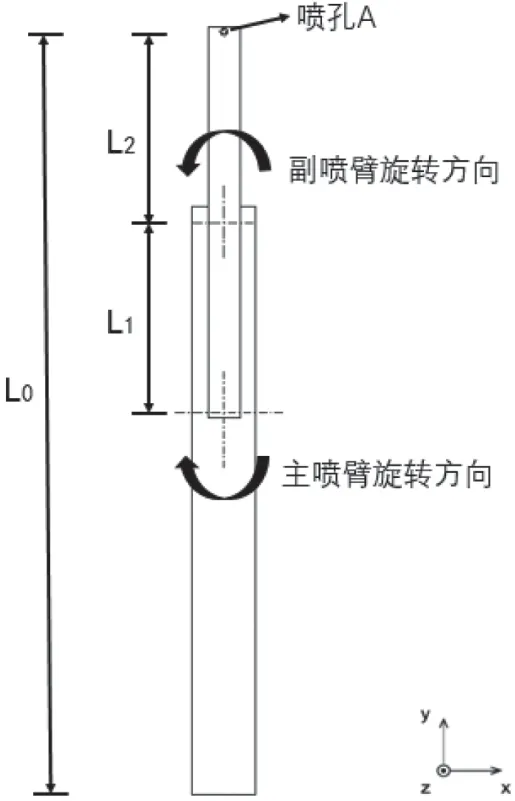
图10 单洗涤喷孔示意图

式中：

XA、YA—喷孔A 的横纵坐标；

θ—主喷臂转过的角度；

L1—主喷臂转轴距副喷臂转轴距离；

L2—副喷臂上喷孔距副喷臂转轴距离；

K—副喷臂与主喷臂转速比，取K=M/N，且M 与N互质。

假设洗涤区域为L0*L0 的正方形区域， 取L1=L2=0.25*L0。

取表中不同转速比K 时，喷孔A 的轨迹曲线如图11（正方形区域边长为L0）。

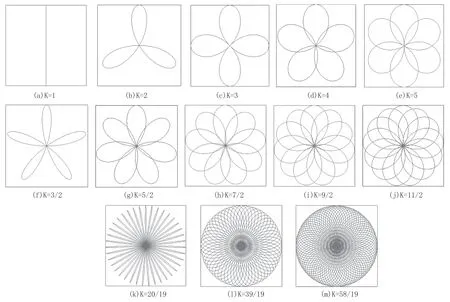
图11 喷孔A 轨迹曲线

如图11 所示有如下规律，见图11（a）～（e），当K 为整数时，K 越大，副喷臂喷孔A 轨迹越密集。当K 为有理数时，K=M/N，M+N 值越大，副喷臂喷孔A 走过的轨迹更加密集（M+N 相等时，K 值越大轨迹越密）。

表2 不同的转速比K

副喷臂依靠单喷孔A 进行洗涤时，推荐选取转速比K 大于3，这样即使出现最差轨迹，单个喷孔的轨迹不会比图（d）更为稀疏。而且相比单转喷臂单个喷孔的圆形轨迹，卫星喷臂单喷孔走过的路径大大加长，到达的喷射位置更多，已经具有轨迹优势。

2.2.2 双洗涤喷孔

如图12 所示，当主副喷臂转向相反，在副喷臂上设置两个洗涤喷孔时，需叠加喷孔B 的轨迹图如图13（灰色为喷孔A 的轨迹，黑色为喷孔B 轨迹）。

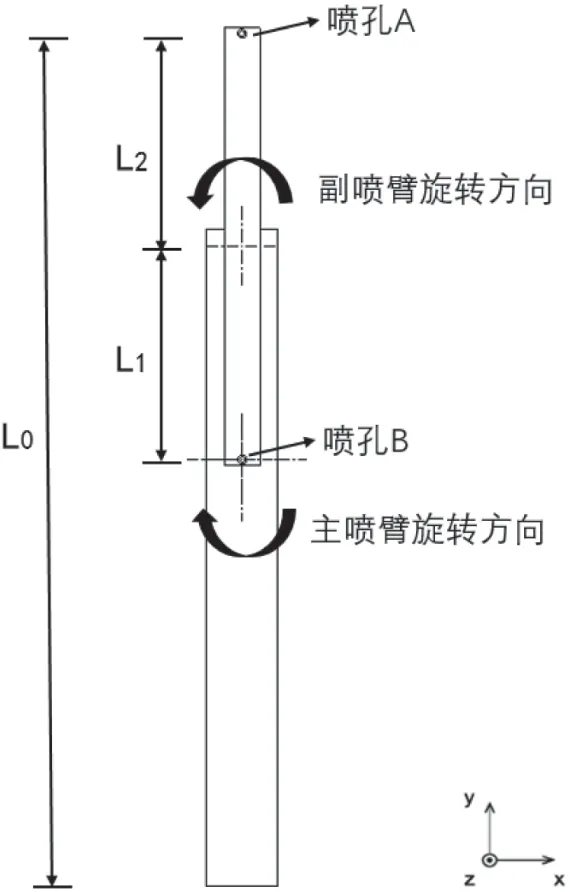
图12 双洗涤喷孔示意图

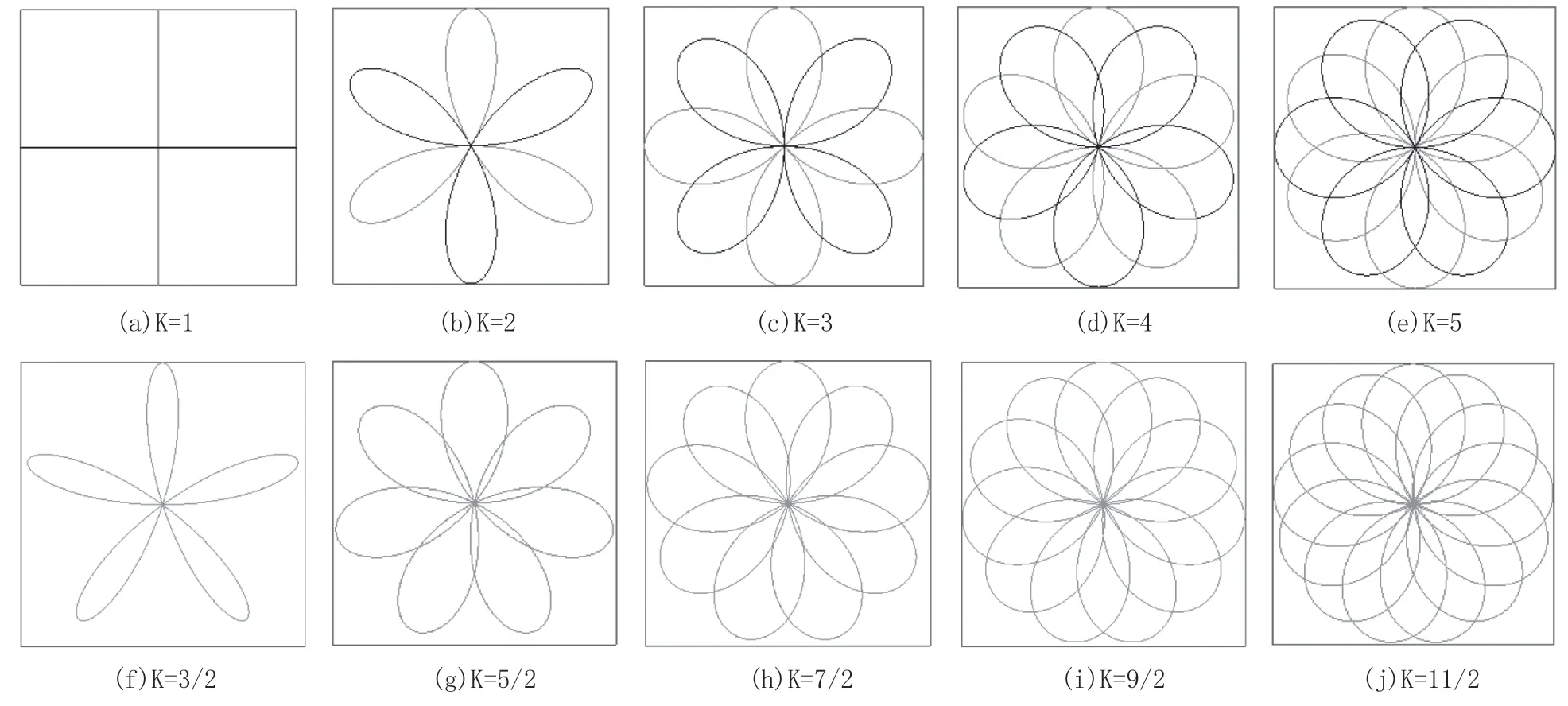
图13 喷孔A、B 轨迹曲线

在副喷臂双侧设置喷孔A 和B 时，虽然对k=1、2、3、4、5 有加密喷射轨迹的作用，但对K 取3/2、5/2、7/2、9/2、11/2 时，两个喷孔轨迹是重叠的，没有加密作用。推荐转速比K 大于2.5，则可能出现的最差轨迹为图13（c），而此时轨迹相比单转喷臂两个同心圆轨迹相比，已经具有优势。

2.2.3 三臂三洗涤喷孔

如图14 所示，当副喷臂形态为3 臂时，设置三个洗涤喷孔，此时喷孔轨迹图如图15（灰色曲线为喷孔A 轨迹，浅灰色曲线为喷孔B 轨迹，黑色曲线为喷孔C轨迹）。

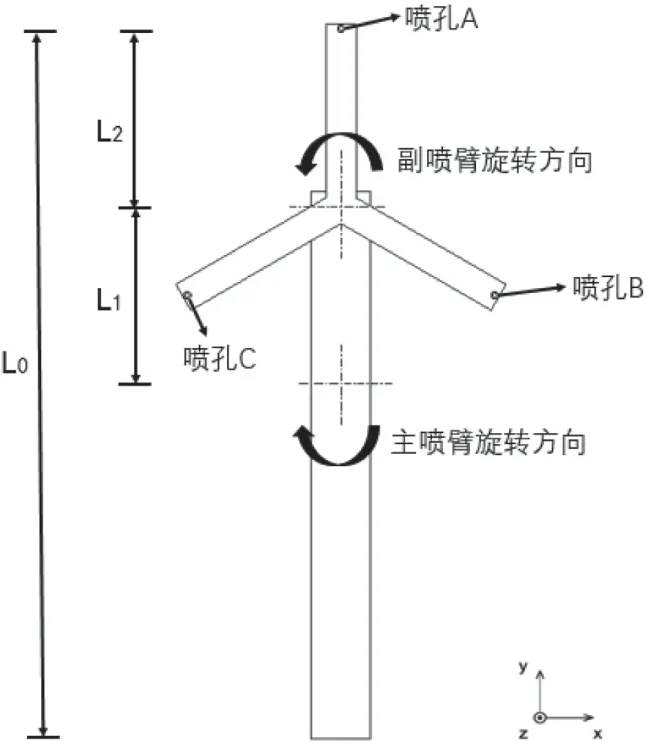
图14 三洗涤喷孔示意图

当副喷臂形态为3 臂，夹角为120°，且在其上设置3 个洗涤喷孔A、B、C 时，虽然对k=2、3、4、5、5/2、7/2、9/2、11/2 等有加密喷射轨迹的作用，但对K取M/N， N=3 时，三个喷孔轨迹是重叠的，没有加密作用。推荐转速比范围K 大于2，取K=7/3 时，轨迹是最稀疏的，但此时三个喷孔的轨迹相比单转喷臂上的3 个同心圆具有轨迹优势。

以上为副喷臂洗涤喷孔轨迹，再叠加驱动孔，以及主喷臂上喷孔的轨迹，方构成完整的洗涤轨迹。当然在喷臂的实际运行情况中，主副喷臂转速受各零件的配合间隙的影响，同时也受洗碗机洗涤过程中的水温、洗涤剂、污染物状态等影响，出现并维持某个固定转速比的臂设计，介绍了主喷臂周期性摇摆式转动和接近匀速转动两种状态；分析了当主喷臂接近匀速转动情况下，旋转方向、转速比及多臂形态副喷臂对喷孔轨迹的影响，并分别给出了在同向转动和反向转动时，对应不同喷臂形态的推荐转速比，避开某些特定转速比下的稀疏轨迹，充分发挥卫星喷臂的轨迹优势，对自由旋转卫星喷臂设计具有一定指导意义。概率极低，且喷臂每次启停时，初始位置都会发生改变，所以即便维持了某个固定转速比，出现了较稀疏的轨迹，但这些轨迹也会随着洗涤泵每次启停旋转一定角度，因此出现大片洗涤死区的概率较低。本文针对不同转向、不同副喷臂形态提出了推荐转速比范围，在喷臂驱动孔设计中参考以上转速比范围，可以进一步降低出现稀疏轨迹的概率。

3 结论

本文主要研究了无齿轮传动系统的自由旋转卫星喷