沿海地区径流对厄尔尼诺南方涛动的响应研究——以浙江省椒江流域为例

蔡周杰,陈 浩*,魏阜森,黄赛花,谢华伟,聂 会

(1. 浙江水利水电学院 水利与环境工程学院,浙江 杭州 310018;2.湖州市水文中心,浙江 湖州 313000)

目前,关于径流对ENSO事件的响应研究已有一定基础,但鲜有研究关注气候变异对沿海地区径流的影响及其响应机理。笔者采用多种方法,对ENSO事件椒江流域中径流变化过程的影响进行探讨,旨在为椒江流域的水文工作提供科学指导。

1 研究区域与数据处理方法

1.1 研究区域概况

椒江流域处于浙江省中部沿海,位于120°14′—121°55′E,28°22′—29°19′N,属亚热带季风气候,东接台州湾,南西北部分别毗邻瓯江、浦阳江、曹娥江等水系。流域形状为三角形,干支流呈树状分布,具体水文站分布情况如图1所示。图中沙段站位于始丰溪支流,柏枝岙站位于永安溪支流。年径流低值区位于天台、仙居两县山间盆地,多年平均径流深700～900 mm,最低值区位于椒北平原等沿海一带。

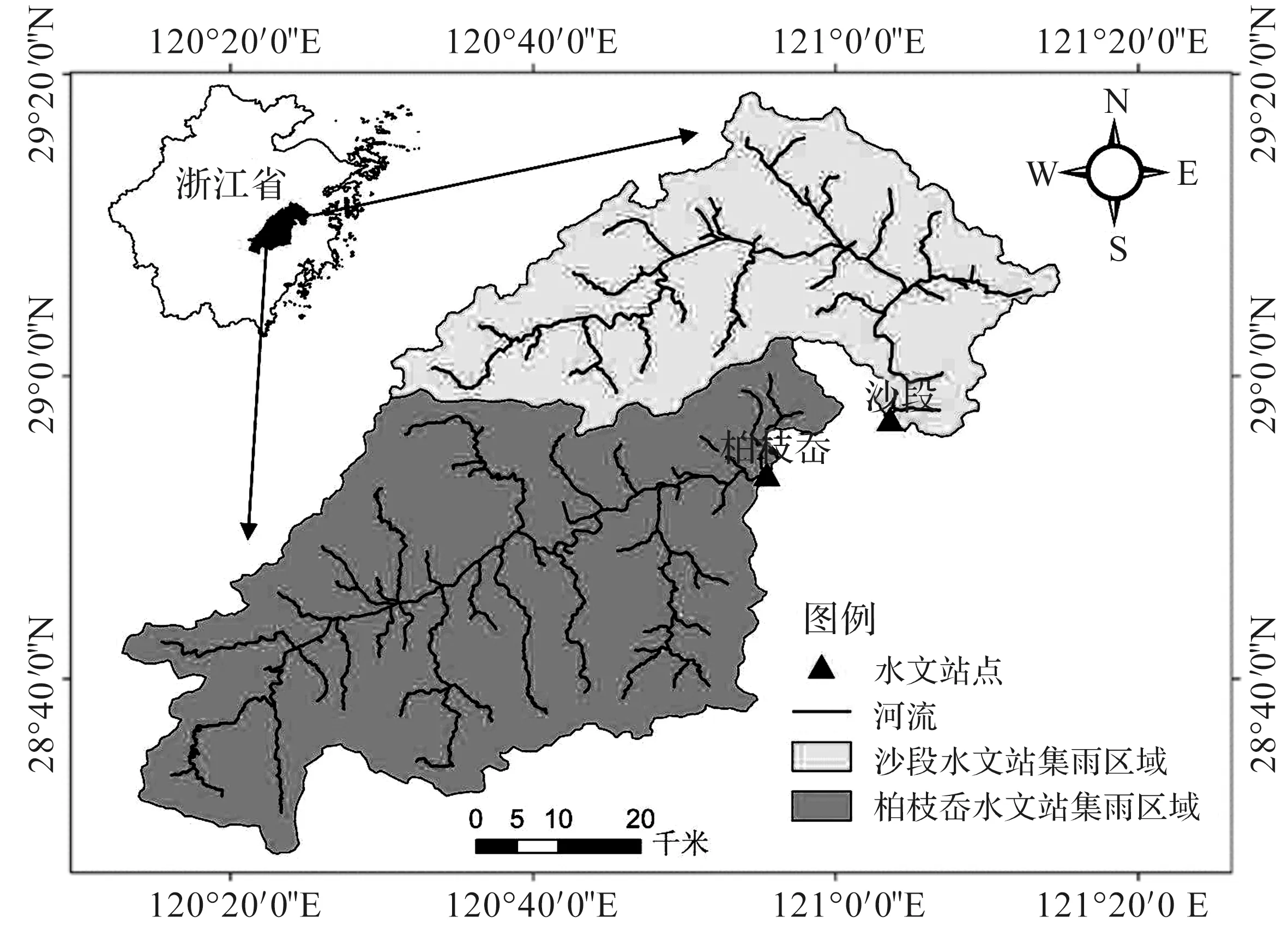
图1 椒江流域水文站点分布图

1.2 数据来源

台州市水文站实时水雨情数据库、台州市防汛专用遥测水雨情数据库提供了椒江流域水文观测站的径流量数据。本研究选取椒江流域的柏枝岙和沙段共两个水文站的径流量数据并对其进行分析,两站点所选数据时间段分别为1957—2018年、1980—2018年。从中国气象局国家气象中心获取有关ENSO事件的评判标准以及在1957—2018年内ENSO事件发生的次数、强度及峰值时间的相关资料。

1.3 研究方法

1.3.1 趋势分析

1) 一元回归分析:该方法是用于研究一个变量如何随另一个或某一些变量变化的方法,用yi代表水文站点为n的径流量,用xi作为yi相应的时间变量,建立yi与xi的回归方程函数。

2) Mann-Kendall趋势检验法:该方法能检验时序数据分布的大致趋势,其趋势表述可分为无明显趋势、上升趋势、下降趋势三类[7]。

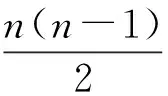
(1)

计算方差值S,即为差值为正的数量减去差值为负的数量,其计算式为

(2)

如果S为正值,那么后部分的观测值相比之前的观测值呈现变大的趋势;如果S为负值,那么后部分的观测值相比之前的观测值呈现变小的趋势。

当n≤10,则需要在概率表中查找S。

当n>10,则计算式为

(3)

(4)

在时序数据趋势的检验中,当ZMK>0时,时序数据存在上升趋势;当ZMK<0时,则时序数据存在下降趋势。

式(1)—式(4)中,f(xi-xj)为差值函数,S为方差,Var(S)为方差S的平均值,ZMK为统计量。

1.3.2Mann-Kendall突变检验

将水文站径流数据按时间依次排列[8],设为X={x1,x2,…,xn},取数据组中后一个数值大于前面所有数值的个数计数值为序列Pk。

(5)

(6)

再将Pk累加得到Sk,即

(7)

计算Sk的方差与平均值,即

(8)

(9)

统计量UFk为

(10)

式(5)—式(10)中:Pk为秩序列;Sk为秩序列的累加值;E(Sk)为Sk的方差;Var(Sk)为Sk的平均值;UFk为统计量。

UFk为标准正态分布,当UFk>0时,则表示数据序列呈现上升的趋势;当UFk<0时,则表示数据序列呈现下降趋势;当|UFk|>UFk时,则表示数据序列的变化趋势是显著的,否则其趋势不显著。

重复以上的计算过程,对计算得到的结果进行倒序并取负值,最后得到的就是UBk统计量序列。将UFk统计量、UBk统计量与临界值U0.05的直线在同一张图上分析。若在两条正负临界直线之间与UFk、UBk曲线相交,那么突变出现的时间就是交点的横坐标。该方法是世界气象组织荐举且已普遍采用的检验方法[8]。

1.3.3Pearson相关系数分析

Pearson相关系数是用来描述两组随机数据统计量的线性相关[9],其计算式为

(11)

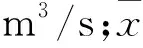
一天，宋太宗和苏易简唠嗑，纵论天下美食，太宗问他：“天下什么东西最好吃？”苏易简说：“臣感觉齑汁为美。”原来苏易简有一次又喝多了，到了深夜，口渴难耐，便来到屋外，以雪洗手，抱着腌菜坛子喝酸菜汁，越喝越觉得好喝。宋太宗听后，哈哈大笑，深以为是。而“物无定味，适口者珍”的论断，也为后世美食家所认可。

1.3.4 小波分析

小波分析可以有效地处理时间序列数据,用于分析径流量和ENSO事件的变化趋势和周期性规律以及它们之间的相互关系等[10]。本研究所用的小波函数计算式为

(12)

式(12)中:ψ(t)为小波函数的复共轭;fb为带宽,BPs;fc为频率,Hz;t为取样时间间隔,年。Morlet小波的实部为Morlet实际值,实部和虚部间存在的相位差可用于消除数据之间的波动。小波方差可用于获得时间序列的主周期,其表达式为

Var(a)=∑(Wf)2(a,b)

(13)

式(13)中:Var(a)为小波方差,Wf为小波系数,a为尺度变量,b为时间尺度变量。小波方差的最大峰值可视为最强振荡,用来分析径流和ENSO事件的振荡变化及平均周期。

2 结果与分析

2.1 椒江流域径流量变化趋势分析

采用一元回归法,以年尺度计算柏枝岙和沙段水文站径流数据的一元方程。两站点的年径流序列变化趋势如图2所示。根据趋势线可知,柏枝岙和沙段的年径流量均呈下降趋势。采用Mann-Kendall趋势分析方法,计算得到柏枝岙和沙段站径流数据两站点的ZMK和S。ZMK分别为-0.34和-0.56,可见两站的径流量呈下降趋势。而S=0,从年尺度上来看,柏枝岙和沙段站点的径流量变化趋势并不显著。

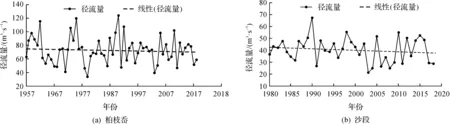
图2 柏枝岙、沙段站点 1957—2018年年径流趋势变化图

2.2 径流量突变分析

根据M-K突变检验分析方法,以年尺度做两站点的突变图,识别研究时段内的径流突变点(图3)。由图3可得,柏枝岙和沙段站的UF曲线与UB曲线分别有13个和8个交点。根据曲线UF与UB的交点及数值可知,以上交点均未突破±0.05的置信水平线,可以大体判定椒江流域年径流量变化比较平稳且没有发生突变。

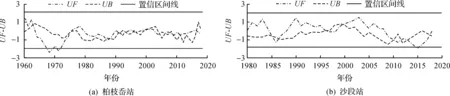
图3 柏枝岙、沙段站点年径流量M-K检验图

2.3 椒江流域径流对ENSO事件的响应分析

2.3.1 Pearson相关系数分析

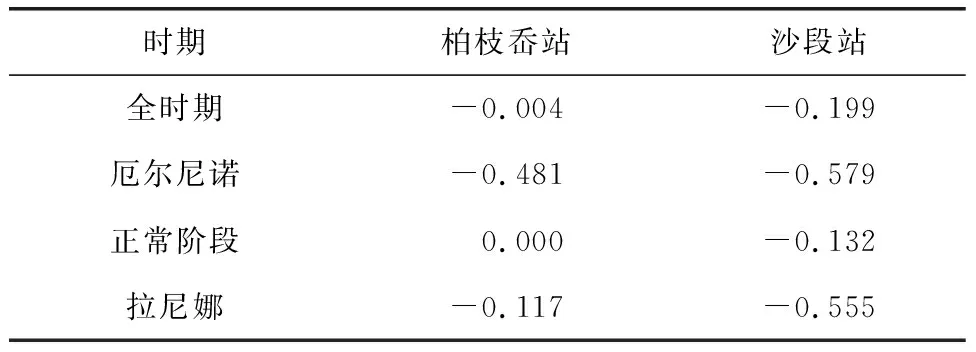
表1 柏枝岙、沙段站年径流量与各时期ENSO指数相关系数

由表1可知,柏枝岙和沙段的年径流量在全时期时与ENSO指数的Pearson相关系数分别为-0.004和-0.199,呈负相关。根据其数值可知,柏枝岙站的年径流量与ENSO事件的强度的相关性并不显著,沙段站的年径流量与ENSO事件强度具有一定的相关性。在厄尔尼诺时期,两站点的年径流量与ENSO指数的Pearson相关系数分别为-0.481和-0.579,呈强烈的负相关。在正常阶段,柏枝岙站的年径流量与ENSO事件不相关,沙段站的年径流量与ENSO事件呈一定程度的负相关。在拉尼娜时期两站点的年径流量与ENSO指数的Pearson相关系数分别为-0.117和-0.555,可知柏枝岙站的年径流量与ENSO事件呈一定程度的负相关,沙段站的年径流量与ENSO事件呈强负相关。从数值上看,厄尔尼诺时期和拉尼娜时期的ENSO指数与径流量的相关系数远高于全时期和正常阶段。由此可知,在厄尔尼诺时期和拉尼娜时期,ENSO事件对椒江流域径流的影响程度更为强烈。

2.3.2 小波分析

对椒江流域年径流量与ENSO指数进行小波分析,年径流量与ENSO指数的连续小波谱如图4所示。由图4可知,在2年、2～4年、4～5年和12年的周期上其显著性均相对较高。柏枝岙站年径流量的4个显著周期与ENSO指数的4个显著周期都有具明显的吻合度,其年径流量与ENSO事件的强度在时、频域上基本一致。沙段站年径流的2 年周期(2007—2011年)与同时段内ENSO指数的2年周期(2010—2011年)也有较高程度的吻合,且ENSO指数在这一显著周期附近的年份也属于高能量区。综上可得两站点年径流量与ENSO事件的强度有着一定程度的响应关系。

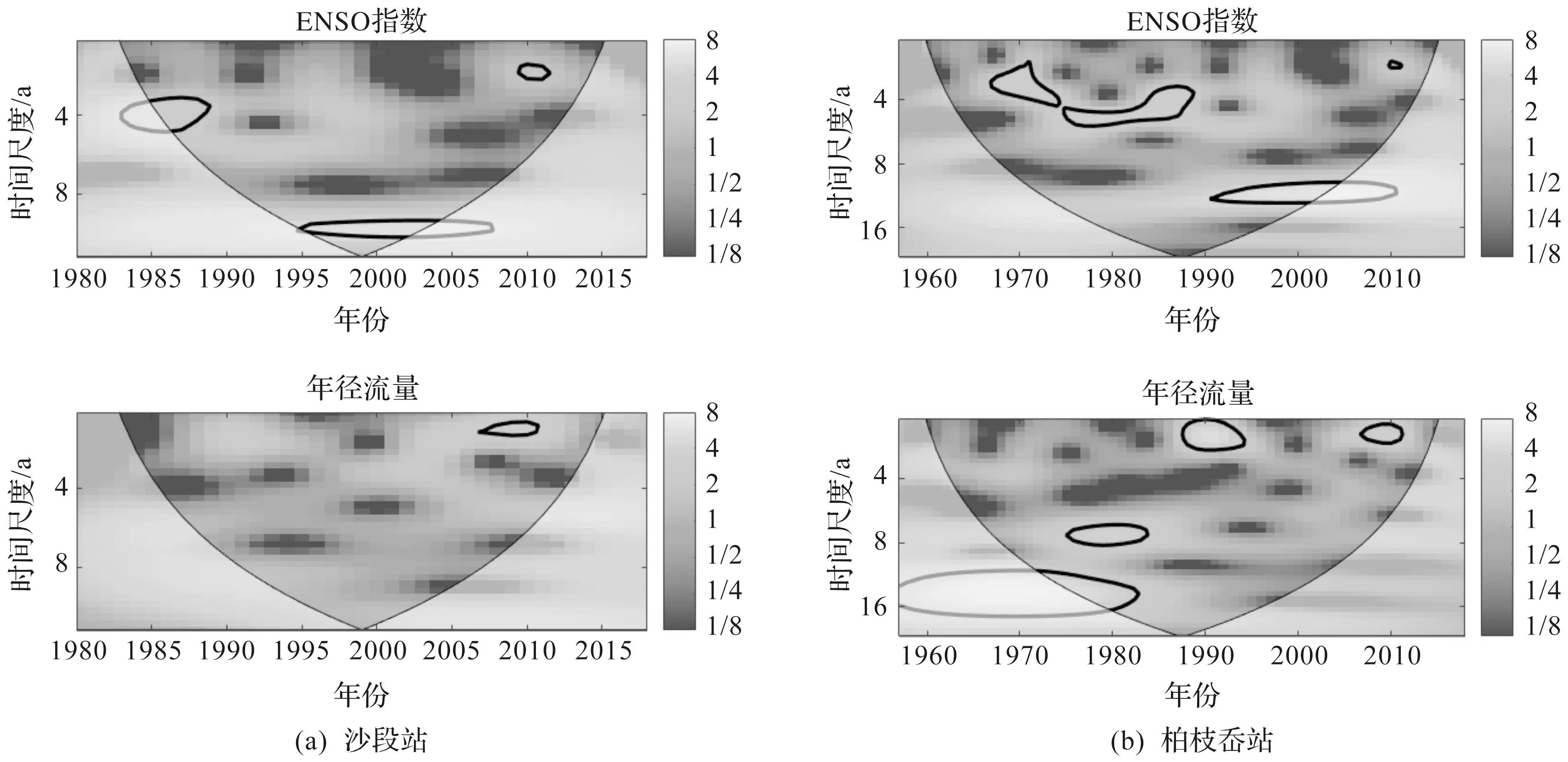
图4 各站点的年径流与ENSO指数的连续小波谱

交叉小波变换虽能较好地进行信号耦合和信号分辨,但是交叉小波变换对于低能量区的解析不够详细,因此需要结合交叉小波能量谱(图5)进行分析。根据图5(a)可知,沙段站径流数据中存在3个显著共振周期,分别为11年周期(1996—2003年)ENSO指数与年径流量呈现正相关,表现为位相差相近;6年周期(1990—1998年)呈正相关,表现为位相差相反;1～3年周期(2007—2012年)呈负相关,表现为位相差相近,虽然这一高能量区未通过置信度检验,但由于这一区域相较于周围能量较高,故可将其放在一起讨论。

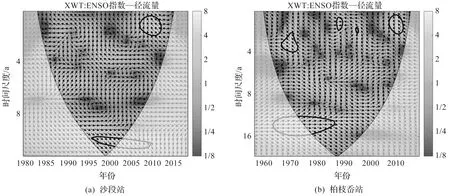
图5 各站点的年径流与ENSO指数的交叉小波谱

根据图5(b)可知, ENSO指数和柏枝岙站的年径流量有着5个显著共振周期,分别为2～4年周期(1966—1973年)呈现负相关,12～16年周期(1973—1987年)呈正相关,2年周期(1986—1990年)呈负相关,3年周期(1994—1996年)以及1～3年周期(2007—2012年)均呈现负相关关系。这些周期中,数个高能量区表明了ENSO指数和年径流量在不同时间段内的相关性。这些分析结果揭示了ENSO指数和年径流量之间的关联关系及其在不同时间段的变化情况。

2.3.3 不同时期年径流差异性分析

为了能更好地分析椒江流域径流对ENSO事件的响应关系,对不同时期柏枝岙站和沙段站的年径流数据进行差异性分析(表2,表3)。通过观察表2可知,柏枝岙站的年径流量在拉尼娜事件时与正常阶段时相近,在厄尔尼诺事件时最小,前者比后者的径流量大8 m3/s。此外,由方差及标准差可知,年径流量在正常阶段时波动最大,在拉尼娜事件时次之,在厄尔尼诺事件时波动最小。由表3可知,沙段站的年径流量在正常阶段时最大,约为44 m3/s,在拉尼娜事件时较小,约为39 m3/s;在厄尔尼诺事件时最小,约为37 m3/s。年径流量在正常阶段时波动最大,在拉尼娜事件时次之,在厄尔尼诺事件时波动最小。通过对表2与表3的分析可知,柏枝岙与沙段的年径流量的基本特征在3种ENSO事件时期大致相同。也可以说椒江流域的径流特征与ENSO事件的类型有一定关联,在厄尔尼诺和拉尼娜事件时径流量偏小,且在厄尔尼诺事件时的影响程度更大。

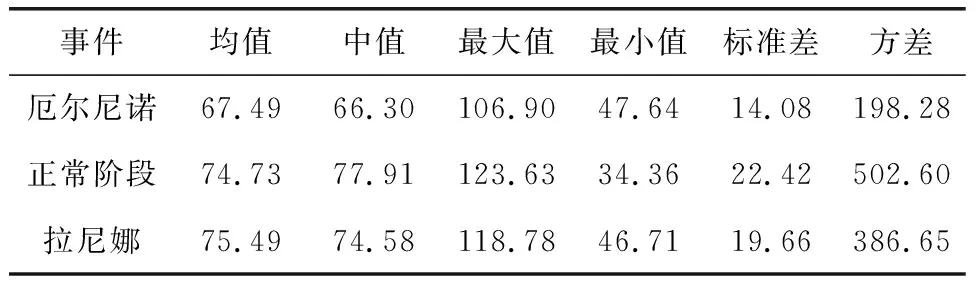
表2 柏枝岙站各ENSO时期年径流统计表 单位:m3/s

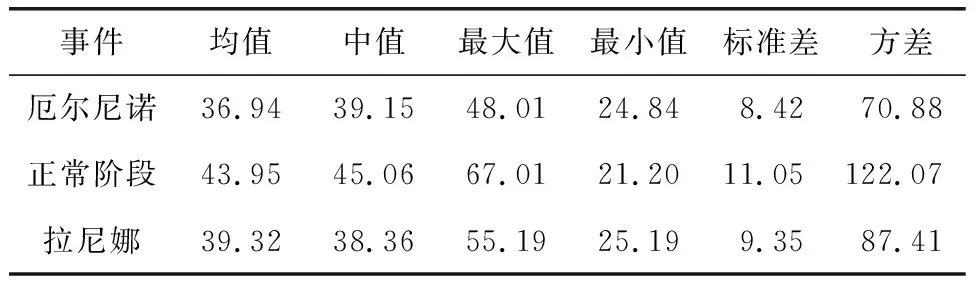
表3 沙段站各ENSO时期年径流统计表 单位:m3/s

3 结 论

以浙江省椒江流域为例,选取椒江流域的柏枝岙和沙段2个水文站的径流量数据和ENSO事件资料进行分析,研究沿海地区流域径流对ENSO事件的响应。主要得出了以下结论:1) 采用一元线性回归法和Mann-Kendall趋势分析法发现这两个流域的径流变化趋势基本相同。同时,通过Mann-Kendall突变检验法,并未发现这两个流域在研究时段内出现径流突变的情况。2)Pearson相关系数分析表明,椒江流域的径流量与不同类型ENSO事件之间呈不同程度的负相关。3)通过分析连续小波谱、交叉小波谱,根据其显著共振周期,不难看出在周期、时间、趋势上都能较好地吻合,由此可知,椒江流域的年径流与ENSO事件的强度、频次均有一定程度的响应关系。4) 椒江流域年径流在不同ENSO时期存在显著的差异性,两个流域在拉尼娜时期的年径流要大于其在厄尔尼诺时期,且年径流在厄尔尼诺事件时波动最小。