基于脑部电阻抗信息的非线性动力学脑卒中诊断方法
2023-10-31施艳艳高振王萌娄亚君杨滨
施艳艳,高振,王萌,娄亚君,杨滨
(1.河南师范大学 电子与电气工程学院,河南 新乡 453007;2.中国人民解放军空军军医大学 生物医学工程学院,西安710032)
脑卒中已成为我国成人致死、致残的首要原因[1].其中,缺血性脑卒中的发病人数约占脑卒中发病总人数的55%~90%[2],一旦发病极容易致残,治愈后复发概率也较高[3].如何降低患者死亡率并改善预后效果,是目前亟待解决的问题.
在临床诊断中,计算机断层扫描(Computed Tomography,CT)和磁共振成像(Magnetic Resonance Imaging,MRI)是常用的监测方法[4-5].然而,CT和MRI不能对缺血性脑卒中的病情发展进行动态监测.电阻抗层析成像(Electrical Impedance Tomography,EIT)作为一种便携无创的动态监测手段,更适用于疾病的早期诊断和床边监护[6].EIT脑卒中监测采用安全电流注入附着在头皮上的一对相对电极中,测量剩余电极对之间的边界电压,以重建检测区域内的电导率分布.然而,电导率重建逆问题具有严重的病态性,易导致重建质量不佳,严重影响诊断的准确性[7].为了提高重建图像质量,国内外学者提出了一些高性能的图像重建算法[8-10],但以上研究主要针对单帧检测信息条件下病态逆问题的求解,缺乏对EIT数据时间序列信息的深入挖掘和分析,难以建立电阻抗信息与脑卒中病情的内在联系,进而实现脑卒中病情的准确诊断.
为了实现脑卒中病情诊断,本文提出一种基于脑部电阻抗信息的非线性动力学脑卒中诊断方法.该方法研究了正常大脑和缺血性脑卒中大脑的电阻抗变化,通过对获取的电阻抗信息进行预处理得到阻抗变化的一维时间序列;研究了2组一维时间序列分别在距离矩阵和递归图上的差异性,采用递归率、确定性和平均对角线长度对2组递归图中非线性动力学参数变化进行定量分析;揭示了由缺血性脑卒中所引发的非线性动力学参数变化;最后通过假手术组和右侧中动脉阻塞组大鼠的实验中验证了缺血性脑卒中会引发阻抗变化的非线性动力学参数改变,并通过统计学分析加以证明.
1 研究方法
1.1 电阻抗信息采集和预处理
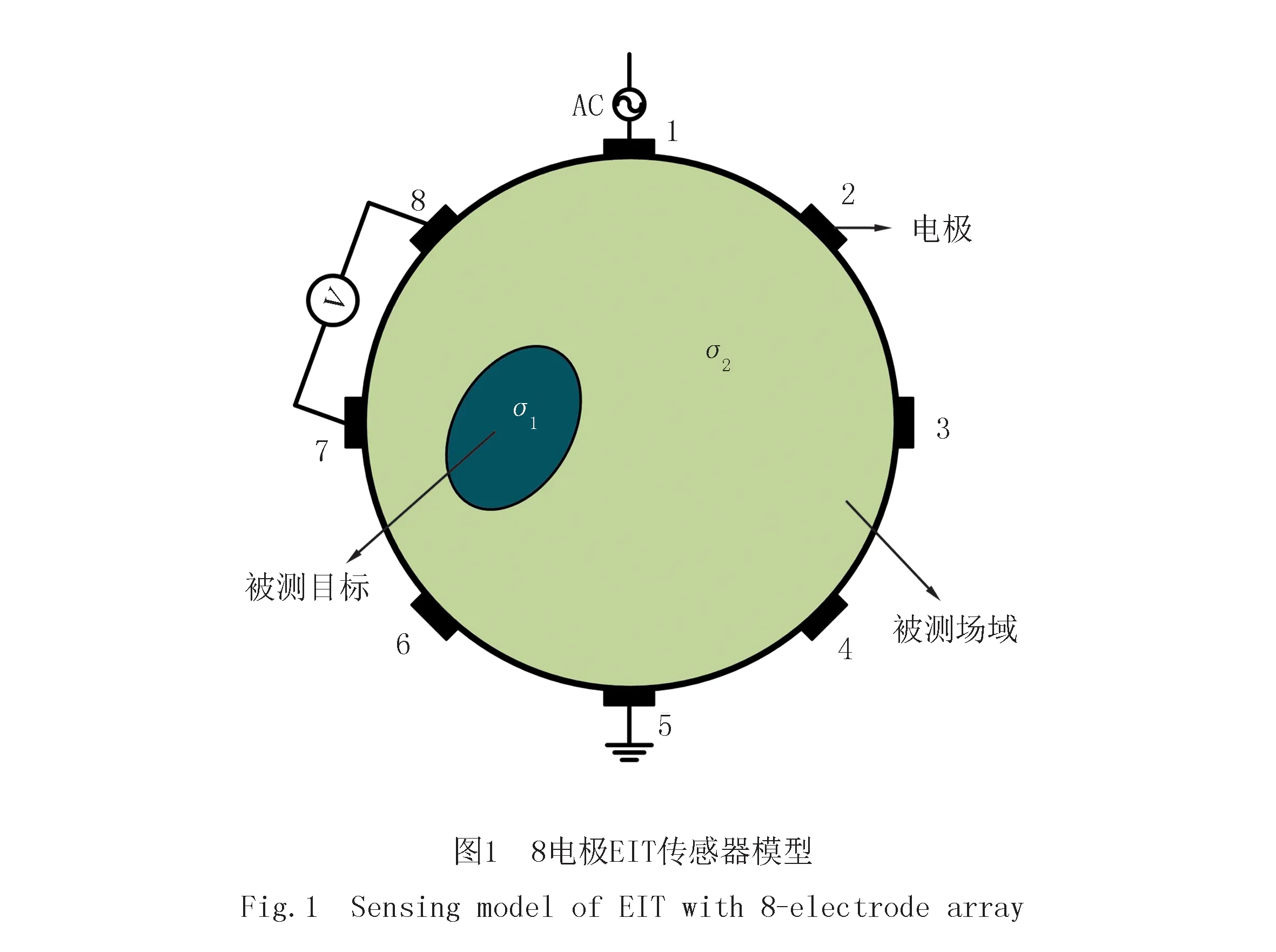
在电阻抗信息采集过程中,电极传感器阵列作为激励源和测量传感器,需在相对电极对上施加电流激励,测量除激励电极外相邻电极之间的电压[11].采用8电极EIT传感器模型进行测量时,每测量一帧数据需要进行8次相对电流激励,每次激励采集除对向激励电极(1和5)外的其余6个相邻电极间的电压信号.每次激励可得4个电压值,故一帧共采集到32个电压数据.图1为8电极EIT传感器模型.σ1和σ2分别表示被测场域中不同介质的电导率.σ1对应脑缺血区域.
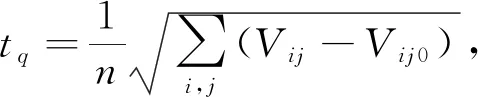
1.2 递归图建立与定量分析方法
根据EIT数据预处理得到的一维时间序列,采用非线性动力学分析方法,建立其递归图[12].
首先,将被分析的时间信号映射到相空间,获得对应的相空间轨迹.通常将时间序列T进行m维的一个拓展,xk=(tk,tk+τ,tk+2τ,…,tk+(m-1)τ),式中,tk表示时间序列T中第k(k=1,2,…,L-(m-1)τ)次激励的值,m为嵌入维度,τ为延迟时间.嵌入维度和延迟时间分别采用假临近法和平均互信息法[13]确定.根据相空间轨迹xk,求出欧式距离Di,j=‖xi-xj‖.最后,求得递归矩阵R.当距离Di,j<ε,Ri,j=1;否则Ri,j=0;式中,ε为阈值,取为原始信号标准差的10%.
进一步,为了更好地描述信号的特性,获取递归点的分布规律,需要对所建立的递归图进行小范围复杂度分析即递归定量分析[14].
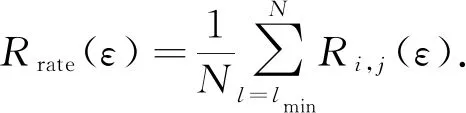
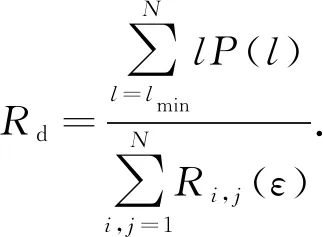
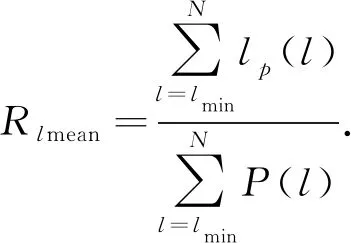
2 研究结果和讨论
2.1 动物模型和数据提取
为了验证该方法对缺血性脑卒中诊断的性能,开展了大鼠模型实验研究.该实验得到中国人民解放军空军军医大学动物研究伦理委员会的批准,并按照该委员会的动物实验指导方针进行.实验系统采用自主研发的FMMU-EIT5系统进行数据采集,正弦激励电流大小为250 μA,频率为50 kHz,采集速度为1 帧/s.实验共采集了8只雄性Sprague Dawley 大鼠(体质量240~270 g)连续监测7 000 sEIT数据.实验中,剃掉大鼠头顶的毛发,并用手术刀切除头顶皮肤和骨膜.在大鼠头顶形成一个冠状方向(宽)2.5 cm,矢状方向(长)3 cm的椭圆区域.将8枚电极(牙钉)沿椭圆区域缘均匀钉入颅骨但不穿透,深度控制在1 mm以下.其中4只大鼠采取右侧大脑中动脉栓塞手术处理,另外4只采用假手术操作进行处理[15].图2为实验数据采集装置和EIT电极排列位置.

2.2 实验结果分析
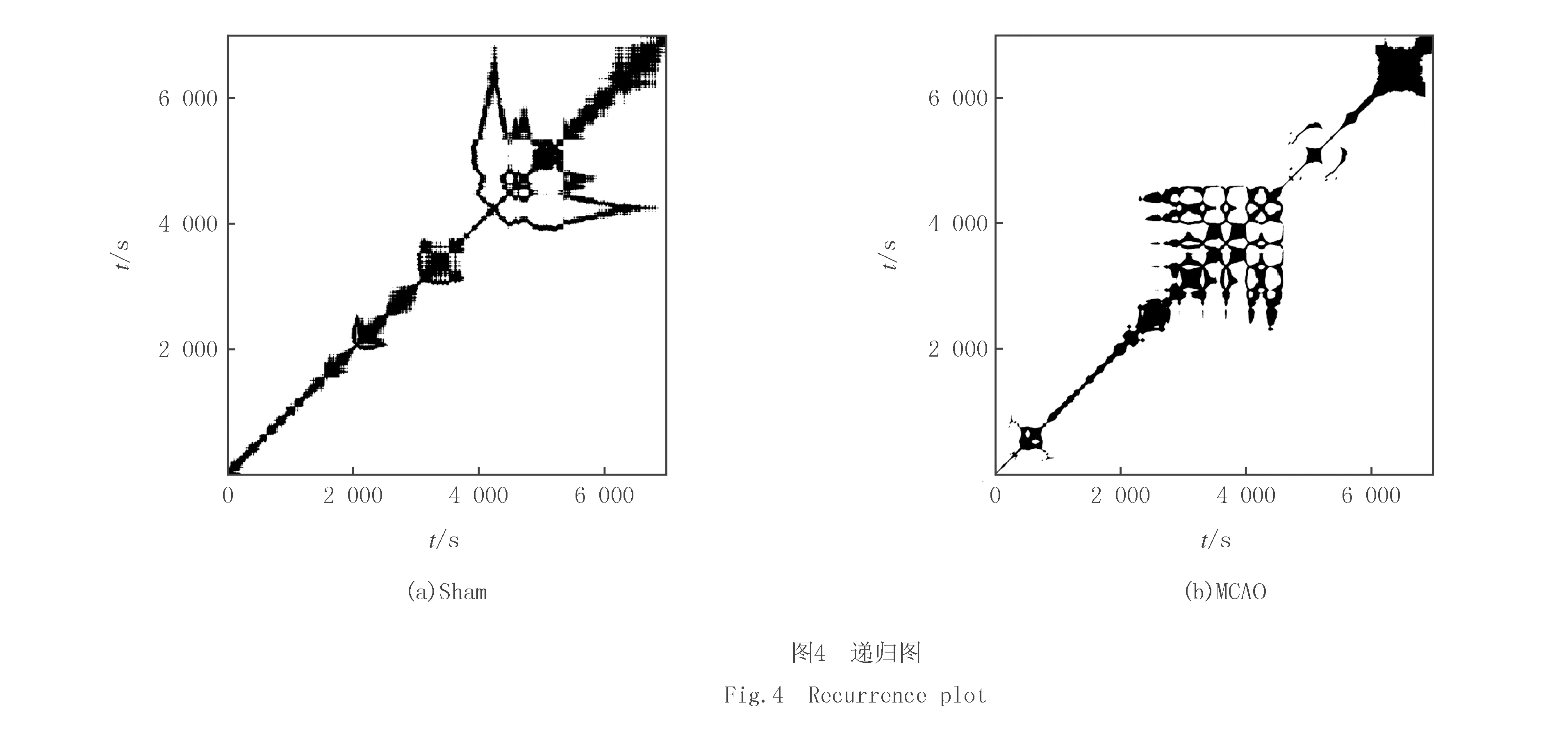
对采集到的数据进行预处理,分别得到术后2组大鼠脑部阻抗变化的一维时间序列{tq}.图3为各组中某只大鼠的数据.从图3(b)可以看出右侧大脑中动脉阻塞组大鼠脑部电压幅值急速上升后趋于平缓,这是由于右侧中动脉阻塞形成后,右侧脑部供血不足所引发的局部阻抗上升.而当被测区域的激励电流不变,在边界上采集到的电压将升高.将2组数据的一维时间序列进行相空间拓展,嵌入维度m=3,延迟时间τ=10,求取距离矩阵D.为了更直观地观察递归状态点的分布特征,求出2组数据的递归矩阵并绘制出对应的递归图(如图4所示,Ri,j=1对应黑点).

从图4可以发现,相对于假手术组,右侧大脑中动脉阻塞组拥有更多的递归状态的点和较为大的块状结构,且递归状态的点出现成块状集中.这表明缺血性脑卒中发生时,脑部阻抗变化的非线性特征显著增加,通过递归图中递归状态点的数量和块状的排布方式可以明显分别假手术组和右侧大脑中动脉阻塞组大鼠.
为了量化分析递归图中递归状态点的分布,分别计算了2组数据的递归率、确定性和平均对角线长度参数,并对这3个参数进行统计分析,以确定其分布是否有差异.附图Ⅰ为递归定量分析参数的箱线图和统计学分析图,其中,箱线图的上下限代表每组参数的最大值和最小值,横线为中位数,小方块为均值.
通过对比附图Ⅰ(a)中2组数据递归率Rrate的均值可以发现,当缺血性脑卒中发生时大脑阻抗变化的递归状态的点增多,递归特性提升.附图Ⅰ(b)右侧中动脉阻塞组大鼠的确定性Rd均值要高于假手术组,表明缺血性脑卒中发生时由于血管阻塞导致大脑局部血流减少,阻抗上升,导致脑部阻抗变化的相关性增强.并且附图Ⅰ(c)动脉阻塞组大鼠的平均对角线长度Rlmean均值高于假手术组.附图Ⅰ(d)中,采用独立分析T检验分别对2组数据的递归率、确定性和平均对角线长度进行统计分析.从附图Ⅰ(d)可以看出,2组数据中递归率和确定性的P<0.05,表明其分布具有显著差异,且平均对角线长度的P<0.01,表明平均对角线长度具有非常显著的差异.通过统计学分析可知,假手术组和右侧大脑中动脉阻塞组大鼠的非线性动力学参数递归率、确定性和平均对角线长度分布具有显著的差异.进一步证明了当缺血性脑卒中发生时,由于大脑部分阻抗上升导致脑部阻抗变化的相关性增强,如递归率、确定性和平均对角线长度升高且在分布上与正常大脑具有显著差异,可以作为诊断脑卒中的依据.
3 结 论
针对现有EIT研究难以建立电阻抗信息与脑卒中病情的内在联系,进而实现对脑卒中病情准确诊断的问题,本文提出了一种基于脑部电阻抗信息的非线性动力学脑卒中诊断方法.通过测量假手术组和右侧中动脉阻塞组大鼠脑部的阻抗信息,并采用非线性动力学的分析方法递归图和递归定量分析提取与缺血性脑卒中诊断相关的非线性动力学特征,将其作为诊断缺血性脑卒中的依据.实验结果表明,假手术组大鼠和右侧中动脉阻塞组大鼠在递归图上具有不同的结构,并且2组递归图的递归率(P<0.05),确定性(P<0.05)和平均对角线长度(P<0.01)具有显著差异.实验结果支持该方法诊断缺血性脑卒中的有效性.
附 录
附图Ⅰ见电子版(DOI:10.16366/j.cnki.1000-2367.2023.06.009).
