随机实验法在社会科学因果分析中的应用
——以女性生育行为的选择效应为例
2023-10-31薛君魏雷东
薛君,魏雷东
(河南师范大学 河南省社会工作与社会治理软科学研究基地,河南 新乡 453007)
因果分析是社会科学研究的难点,休谟认为因果关系需要具备相关性、时间性和必然性三要素[1],即A和B相关,A必须发生在B之前和所有其他的因素C都已经被排除,只有同时满足上述3个条件,才能说A和B之间存在着因果关系.随机实验方法可以同时满足这3个条件,是因果推论的唯一可靠方法,这是目前科学界的共识[2],在所有因素已知、未知或者无法严格控制其他因素的前提下,可以通过实验构造“实验组”(Treatment Group)和“对照组”(Control Group)的双盲法(Double Blind)来分析核心自变量对结果变量的影响.但在社会科学领域,由于受研究伦理等限制,因果分析中很难具备必然性条件,社会科学研究常用的非随机性分析的多元统计模型只能有效检验休谟因果律的相关性,不能完全检验因果律的必然性[3],统计模型再精巧,也只是对密尔因果分析逻辑的近似模拟[4].基于观测数据的各种统计模型分析控制只是近似满足因果分析[5],如何基于观测数据,在研究设计中利用自然科学中随机试验思路控制所有的混淆变量来探讨因果关系成为当下社会科学研究的热点.
本文提出在研究设计中利用自然科学随机试验思路控制所有混淆变量,以满足因果分析中的必然性.同时为社会科学研究中因果关系的探讨提供一定的参考.
1 社会科学领域因果分析的难点
1.1 社会科学研究中的数据局限
在社会科学领域,由于受研究伦理等限制,无法像自然科学那样做“控制实验”,所获得的数据一般不是“实验数据”,而是自然发生的“观测数据”,按其性质大致可分为3种类型:横截面数据、时间序列数据和面板数据.横截面数据是指多个行为个体变量在同一时点上的描述取值,时间序列数据是指某个行为个体变量在不同时点上的描述取值,面板数据是指多个行为个体变量在不同时点上的描述取值.
由于观测数据缺乏人为控制,这就给干预构造实验组和对照组探索因果关系带来一定的挑战.
1.2 社会科学研究中的方法局限
在社会科学常用的线性回归模型中,高斯-马尔科夫定理指出普通最小二乘法(Ordinary Least Squares,OLS)能满足最佳无偏线性估计,即“BLUE”(Best Liner Unbiased Estimator)特性的前提是自变量独立于误差项且误差项的均值为零,可以理解为yi=α+βxi+εi,其中εi是完全随机决定的,故而xi与εi相互独立,Cov(xi,εi)=0,因此无论是否有遗漏变量,OLS估计都是一致的,且E(εi|x1,…,xn)=0,满足模型中的外生性假定,OLS估计也是无偏的.其中,随机性是外生必然性的保证,这就是OLS估计中的正交假定,即误差项与自变量不相关,是完全随机的,违背正交假定就会产生内生性问题.一般而言,产生内生性问题的原因主要有3种:遗漏解释变量、解释变量测量误差和双向因果关系.内生性问题会使得参数估计结果有偏且非一致,进而导致因果关系的识别结果不可靠,而引入随机性是解决回归模型中内生性问题的根本.
2 随机实验法引入社会科学因果分析的探索
随机实验的思路是在已知所有因素的前提下,控制{x2,…,xk},观察因变量y的变化.或在所有x因素未知或者无法严格控制{x2,…,xk}其他因素的前提下,可以通过随机性构造“实验组”和“对照组”来分析实验因素对结果变量的影响.其中的关键点是控制或者随机性来达到“实验组”和“对照组”的“总体相同”,继而实施不同的干预,通过处理效应的差异来获得真实的因果关系.因此,能否在社会科学研究中构造出总体相同的实验组和对照组是因果分析的关键.
2.1 自然实验的研究思路
实验设计是揭示变量之间因果关系最有效的工具,假定{x1,x2,…,xk}包含了所有可能影响因变量y的因素,相关研究设计可分为控制实验,随机实验,自然实验.
在社会科学领域,由于研究伦理等限制,很难通过人为干预构造实验分组,一般会采用自然实验的方法来探索变量间的因果关系[6].自然实验是指某些并非实验目的的随机性事件构造了实验组和对照组,且在两个分组之间施加不同的自变量影响,最终得出自变量对因变量真实影响,在自然实验中,自变量x对因变量y的因果效应可以简单地表现为条件期望的差别,即E(y|X=x)-E(y|X=0).自然实验虽然能够揭示真实的因果关系,但与研究主题相关的数据可遇不可求.
2.2 倾向值匹配的研究思路
在社会现象是多因、随机的和未知的前提下,FISHER[7]提出通过随机实验来达到“总体相同”的必然性,即大数定理保证了实验对象的各种不可控差异被随机化分配平均了,实验组和对照组之间“总体相同”.如果社会现象是在已知、清晰和可控的前提下,能否通过已知的混淆变量构造出实验组和对照组?倾向值匹配分析方法试图基于多维混淆变量构造不同的分组并进行因果分析.
倾向值匹配是基于反事实框架下的因果分析方法,即在可忽略性假定下,利用观测数据按照一定的原则在实验组和对照组之间进行匹配,从而控制由于选择偏差(Selection Bias,SB)带来的混淆变量,得到参与者平均处理效应(Average Treatment Effect on the Treated,ATT)[8].具体逻辑为:
如果ATT=E{Yi(1)-Yi(0)|D=1},那么实验组和对照组之差可分解为
E{Yi(1)|D=1}-E{Yi(0)|D=0}=(E{Yi(1)|D=1}-E{Yi(0)|D=1})+(E{Yi(0)|D=1}-E{Yi(0)|D=0})=ATT+SB,
其中,D=1表示接受干预的分组,D=0表示未接受干预的分组.因此通过倾向值匹配,采用类实验的方法控制选择偏差,在观测数据的基础上获得真实的处理效应.
总之,在社会现象是多因、随机和未知的前提下,随机性的引入是社会科学因果分析的关键,在社会现象是已知、清晰和可控的前提下,可以利用倾向值匹配基于反事实框架,降维构造实验组和对照组探讨社会科学中的因果关系.
下文以女性生育行为的选择效应为例,详解自然实验与倾向值匹配法的应用.女性生育行为的选择效应可以理解为女性不同的个人特征、家庭禀赋和工作环境等因素既会影响女性的生育行为,也会影响其市场劳动参与收入.在研究女性生育行为对其市场劳动收入影响时,首先需控制生育行为之外对女性市场劳动收入有影响的混淆变量,再叠加不同的生育行为,最终获得女性生育行为对其市场劳动收入影响的真实因果关系.同理,在研究女性市场劳动参与对其生育行为影响时,首先需控制市场劳动参与之外对女性生育行为有影响的混淆变量,再叠加是否参与市场劳动,最终获得市场劳动参与对其生育行为影响的真实因果关系.
自然实验法在生育行为选择效应的应用可以理解为通过一孩性别的随机性分组,可以保证男婴组和女婴组一孩生育前女性的个人特征、家庭禀赋和工作环境等混淆变量总体相同,再叠加不同的多孩生育行为,来测量女性多孩生育对其收入真实的影响.而倾向值匹配法的应用重点关注“谁是职业女性”,通过倾向值计算把与职业女性生育行为相关的混淆变量降为一维,并在职业女性与非职业女性之间进行配对,形成实验组和对照组以消除职业女性与非职业女性之间由于混淆变量形成生育水平的选择性差异,即两者的生育行为的差异只来源于参与市场劳动这一因素.
3 案例分析
3.1 自然实验法在女性多孩生育惩罚效应研究中的应用
生育事件对女性收入影响的因果分析涉及女性个人特征、家庭禀赋和工作环境等混淆变量的控制[9],传统的多元统计模型很难克服众多的遗漏变量导致的内生性问题,案例采用自然实验的研究设计,来达到一孩生育前女性“总体相同”的必然性[10],即大数定理保证了影响女性收入的各种不可控差异被随机化分配平均了,通过一孩性别随机分组保证男婴组和女婴组一孩生育前女性的个人特征、家庭禀赋和工作环境等混淆变量总体相同,然后在性别偏好外生性的假设下叠加不同的多孩生育行为,通过类实验干预后的组间差异来测量女性生育收入惩罚效应的差异.这种随机实验的研究设计包含了生育前后的时间变化,基于一孩生育前变量控制去对比多孩生育对收入的影响可以有效控制生育行为的选择效应.具体表示如下:i代表了实验组与对照组的虚拟变量,可以设定i=1为实验组,i=0为对照组;t代表了时间要素,t=1为实验前,t=2为实验后.结合女性生育收入惩罚效应的虚拟变量如下:
通过一孩性别的随机分组把女性生育多孩的收入惩罚效应分解为分组效应Gi(Group-specific Effects)和时间效应Di(Time-specific Effects).
当t1为不育时:yi1=β0+β2Gi+εi1,当t2为多孩生育时:yi2=β0+β1GiD2+β2Gi+γ+εi2.
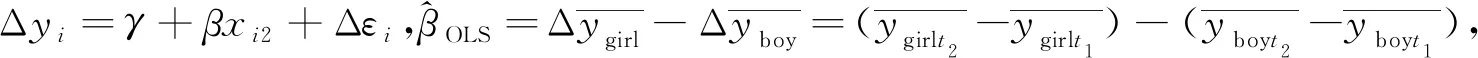
基于以上研究思路,利用2017年全国生育状况抽样调查数据,引入自然实验,通过一孩性别随机分组控制女性生育前个人特征、家庭禀赋和工作环境等难以观测的混淆变量,然后在男孩偏好下叠加不同的多孩生育行为,来对比分析城乡女性多孩生育收入惩罚效应的差异.
3.1.1一孩性别的随机性分组的均衡性检验
相关研究已经证实了我国一孩的出生性别是外生的、随机的,不存在人为干预的一孩性别分组满足随机性要求[11],从表1一孩性别的随机性分组的均衡性检验结果也印证了相关研究结论,即女性的年龄、婚姻状况、民族、受教育程度、健康状况,配偶的健康状况、就业状况、主要职业、单位性质和照料替代多个方面的相关变量在一孩男婴和一孩女婴分组间都不存在显著性差异(5%和1%水平).结合人力资本和补偿工资理论,可以看出一孩性别的随机分组能够很好地控制影响女性生育收入惩罚效应且难以观测的个人特质、家庭禀赋和工作环境因素,从而为多孩生育行为对女性收入高低、就业状态影响的无偏估计奠定了分析基础.
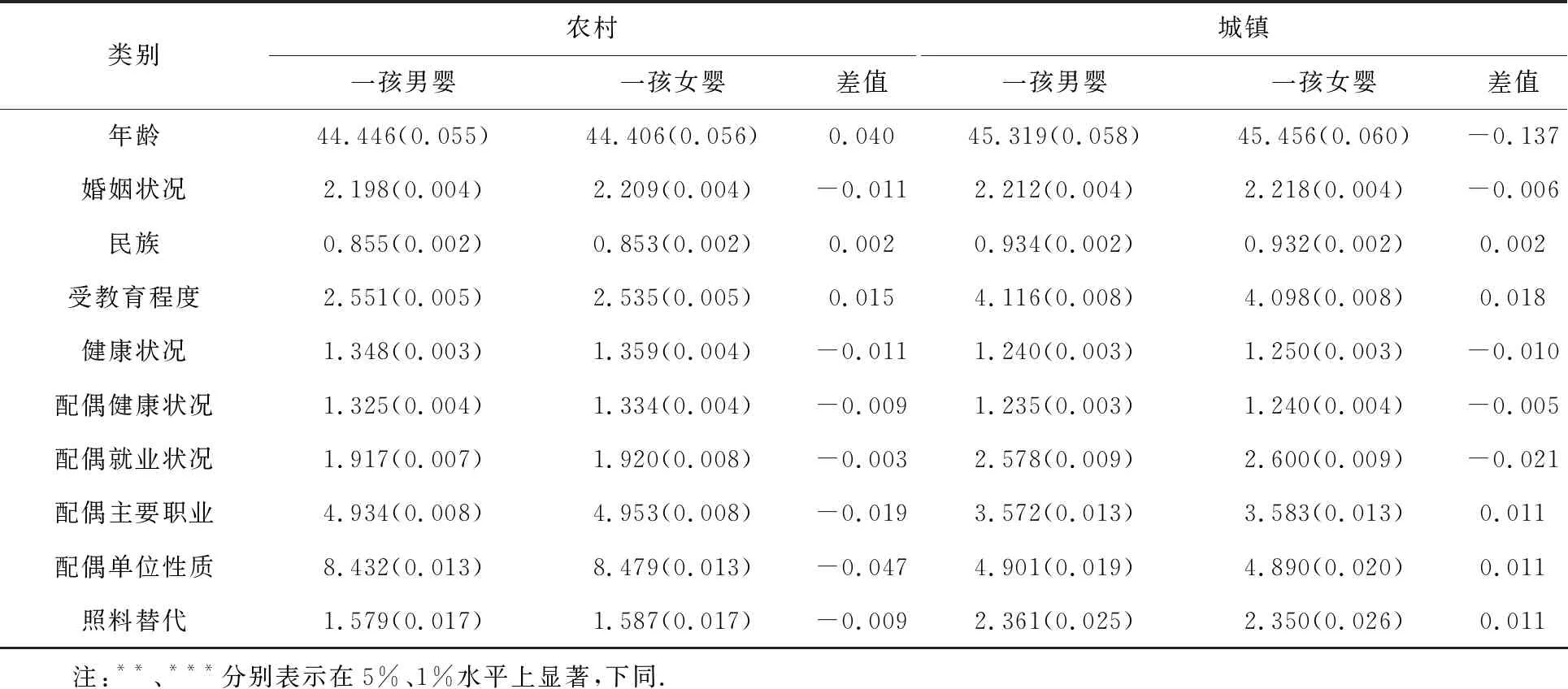
表1 一孩性别随机性分组的均衡性检验
3.1.2女性多孩生育的收入惩罚效应
生育数量、生育意愿和是否有不满六周岁孩子的对比结果发现(见表2),一孩女婴组女性多孩生育行为和意愿水平显著多于一孩男婴组女性,这一研究结论验证了男孩偏好下的一孩女婴多生育行为的研究假设,也间接证明了本文基于一孩性别随机性分组分析多孩生育行为惩罚效应的可行性.
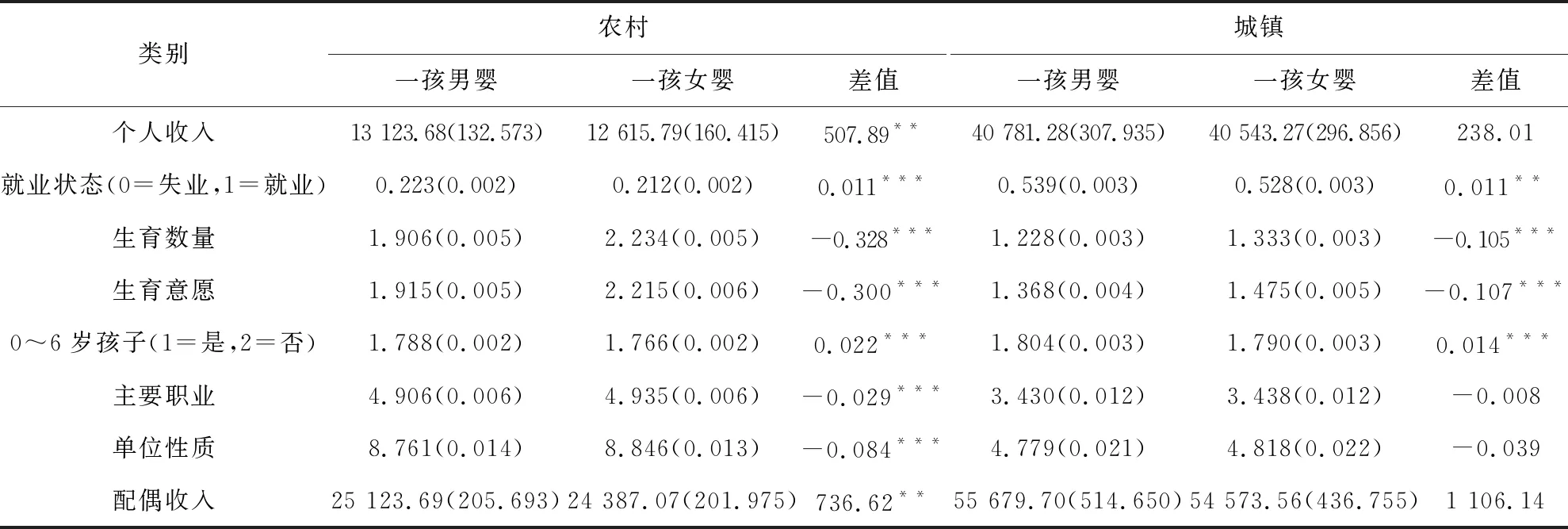
表2 女性多孩生育收入惩罚效应差异的城乡对比
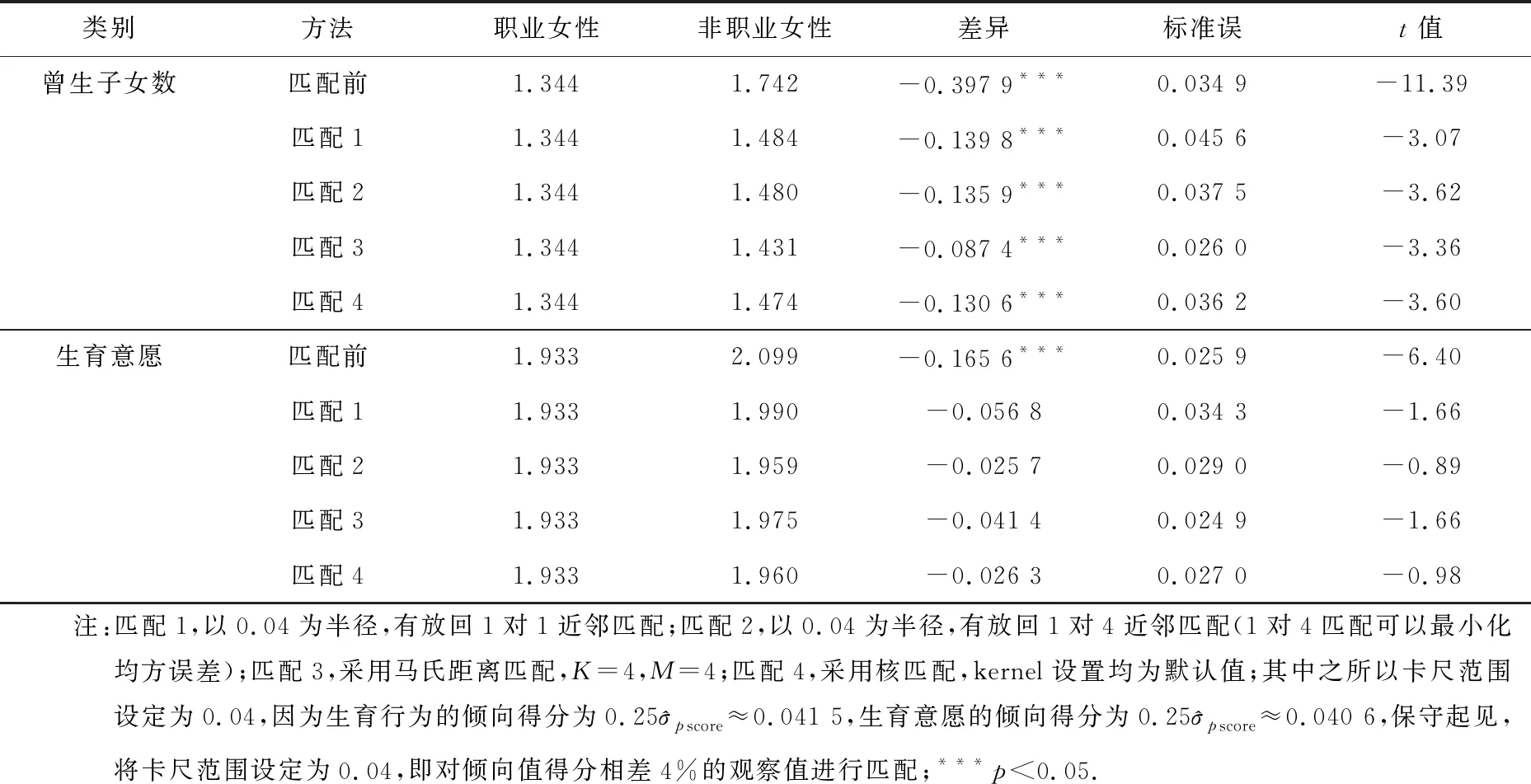
表4 生育行为和生育意愿的平均处理效应
分析结果显示:存在男孩偏好下多孩生育行为差异.无论城乡都存在显著的男孩偏好,体现为一孩女婴组的多孩生育数量和生育意愿显著大于一孩男婴组,区别为农村男孩偏好较强,城镇男孩偏好较弱.这种性别偏好下的多孩生育行为差异构建了通过一孩性别的随机分组,测量多孩生育行为惩罚效应的研究设计,即“总体相同”分组间,多孩生育行为不同是否会造成女性收入、就业状态的差异;城乡女性多孩生育存在一定的收入惩罚效应,两者的差异体现在农村女性多孩生育的收入惩罚效应显著高于城镇女性,且多孩生育对农村女性收入和就业状态都有着显著负面影响,而对城镇女性影响只体现为短暂的工作中断,对收入影响不显著.
3.2 倾向值匹配在职业女性低生育行为分析中的应用
相对于非职业女性,职业女性的低生育行为既有可能来自职业女性高学历,城镇户口,高社会阶层和更为开放的生育观念等与生育行为有关的选择性特征[12],也有可能来自参与市场性劳动而提高的生育机会成本、职场生存压力和家庭照顾压力等与劳动相关的生育困境[13].探讨市场劳动参与对职业女性生育行为的影响必须分离出选择效应才能得出真实的因果关系[14].因此本案例基于2015年中国综合社会调查数据(Chinese General Social Survey,CGSS),利用反事实框架的倾向值匹配方法,在控制学界已认同的年龄、教育程度、户口、家庭收入、社会阶层和生育观念等混淆变量下探讨职业女性和非职业女性生育行为的差异是否存在选择效应,以及劳动参与率提高是否降低女性的生育行为.
具体的研究思路为通过倾向值计算把与职业女性生育行为相关的混淆变量降为一维,并在职业女性与非职业女性之间进行配对,形成实验组和对照组以消除职业女性与非职业女性之间由于混淆变量形成生育水平的选择性差异,即两者的生育行为的差异只来源于参与市场劳动这一因素,在CGSS截面数据的基础上以准实验的方法分析劳动参与和生育行为之间的因果关系.其通过倾向值配对思路化解了对影响职业女性生育水平的多维特征难以控制的难题,并通过反事实的分析在只有观测数据的基础上得到劳动参与和生育行为之间因果关系的结果.
一定意义上,可把倾向值匹配分析方法视为一种再抽样,即通过匹配再抽样的方法使得观测数据尽可能地接近随机实验数据,本文选用了最近邻居、马氏距离和核匹配3种匹配方法,并对比各自的分析结果,以测试方法的稳健性.
3.2.1匹配的均衡性检验
倾向值匹配的均衡性检验是考察匹配结果是否较好地平衡了数据,是匹配质量好坏的检验.下文以最近邻居匹配方案为例,在0.04卡尺范围设定和有放回1对1匹配下,通过stata命令pstest的匹配结果.匹配前后各混淆变量在职业女性和非职业女性的两个分组之间标准化偏差和显著性变动可以看出,匹配后大部分变量标准化偏差都在10%以内,且两组间的差异都不显著,虽然教育程度和户口分布两个变量匹配后差异依然显著,但两者的标准化偏差分别下降了50.2%和18.5%,说明了匹配的整体均衡性较好.
3.2.2生育意愿与生育行为分析
不同因变量和不同匹配方法的平均处理效应分析结果可分为3部分,即匹配前的差异、匹配后的差异和不同匹配方法下结果差异以测试匹配的稳健性.
首先,从匹配前生育意愿与生育行为的差异可以看出,职业女性都显著低于非职业女性.具体为职业女性的曾生子女数低于非职业女性0.397 9,职业女性如果没有政策限制的话,希望的孩子数低于非职业女性0.165 6.这种差异既有可能是由于参与市场劳动导致的,也有可能是由于职业女性选择偏差的结果.
其次,结合匹配后的两组之间生育意愿和生育行为的差异可以得出,控制选择效应后不同匹配方法下生育行为差异依然显著,即职业女性曾生子女数显著低于非职业女性,利用反事实因果推断可以解释为职业女性如果不参加工作的话,他们的平均生育子女数应该比现在职业女性要高,说明了劳动参与显著降低了职业女性的生育行为;而不同匹配方法下控制混淆变量的生育意愿差异都不显著,即希望的孩子数在两个分组间没有差异,说明了劳动参与对职业女性的生育意愿没有显著影响.
最后,对比不同匹配方法下的分析结果可以看出各系数的方向性和显著性保持一致,生育行为和生育意愿的平均处理效应是稳健的.以曾生子女数为例,最近邻居、马氏距离和核匹配3种平均处理效应结果差异都为负且T检验显著,而希望孩子数的3种平均处理效应结果差异为负且T检验不显著.从具体系数值来看,不同匹配方案下变化也很小,说明了以上分析的结果是稳健的.
4 结论与讨论
本文提出在研究设计中利用自然科学随机试验思路控制所有混淆变量,以满足因果分析中的必然性.生育行为选择效应的案例分析结果显示:(1)自然实验法与倾向值匹配法都能较好的控制混淆变量的影响,组间均衡性检验结果验证了“实验组”和“对照组”的“总体相同”假设;(2)女性多孩生育行为对其市场劳动收入影响分析来看,城乡女性多孩生育存在一定的收入惩罚效应;(3)女性市场劳动参与对其生育行为影响分析来看,女性参加工作而产生的成本与效用权衡和工作与家庭失衡成为生育行为的抑制因素.
对比组间均衡性检验结果可以得出,自然实验法对混淆变量的控制优于倾向值匹配法,但随机性条件的满足在人文社科研究中可遇不可求,适用面更宽广的倾向值匹配法再抽样研究设计不失为一个有效的补充,在社会现象是已知、清晰和可控的前提下,也能大体做到实验组和对照组之间的“总体相同”.
进一步讨论认为:随着社会科学的研究重点由统计推断向因果关系识别转变,分清相关关系和因果关系显得尤为重要.其中相关关系仅指二者在变化趋势上存在着某种程度的一致性,而因果关系强调的是二者之间存在的某种理论逻辑上客观规律的联系.传统意义上的统计推断是基于成熟理论思辨,借助统计学模型,利用样本信息对总体进行参数估计,依靠假设检验以判断估计结果的统计显著性,从而识别所谓的因果关系.但是,这种统计推断由于内生性等问题,其对因果关系的识别并不可靠.利用随机实验的思想,根据混淆变量的特性在研究设计中引入随机性或人为构造实验组和对照组,以达到总体相同的必然性,继而识别因果关系是十分有意义的探索,其中包括了反事实理论框架思想,自然实验、倾向值匹配、断点回归、双重差分、工具变量等方法的应用.
