利用低数据率HRRP序列进行弹道中段目标识别
2023-10-31韦楠楠张兴敢
袁 雪,韦楠楠,张兴敢
(南京大学电子科学与工程学院,江苏南京 210023)
0 引言
随着周边国家洲际导弹的成功试射和该领域的迅速发展,我国现代弹道导弹防御系统面临着巨大的挑战,其中区分弹头目标和诱饵目标给导弹防御系统提出了更高的要求。相控阵雷达作为导弹防御系统主要探测手段,可同时执行多目标搜索与跟踪,但其工作能力会受到雷达时间资源、雷达辐射信号总能量等因素的限制。因此,通过合理利用雷达信号能量,以及改善信号处理等方式,有利于提升整个雷达系统的性能。
雷达目标识别的基本途径,是从目标后向电磁散射中提取目标的结构特征和运动特征,再根据一定的先验信息来辨别真伪,结构特征包括目标的尺寸、形状、材料等,是鉴别真假目标的直观属性;运动特征包括宏观弹道特征和运动特征,它们从不同侧面反映目标的本质属性[1]。对于已稳定跟踪的目标,采用宽带雷达可提取更多的目标特征信息,目标HRRP(High Resolution Range Profile)则是用宽带雷达信号获取的目标散射点的子回波在雷达射线上投影的矢量和,它提供了目标散射点沿距离方向的分布信息,其包含了有关目标的结构、大小和形状等信息,便于对目标进行分类、识别。
目前大多数基于HRRP 序列特征的研究主要是利用中、高重复频率的雷达发射脉冲,以达到高精度的目标参数测量。文献[2]利用弹头目标的径向长度序列的极值信息估计出进动参数和形状参数的耦合结果,再根据径向长度序列构造一个辅助函数来实现进动参数和形状参数的解耦,最终利用提取的参数信息进行目标识别。文献[3]提出了通过计算距离像序列最大滑动相关系数变化的方法来进行周期以及频率提取。文献[4]通过对相邻一维距离像进行差分计算降低其他频率成分,增强进动频率成分再进行提取,避免了因目标散射点分布模型变化而导致的估计误差。文献[5]利用散射中心位置变换规律,基于广义Radon 变换来估计空间弹道的目标进动频率等微动参数。然而对于远程雷达来说,雷达需发射宽脉冲以保证有足够的辐射能量来获取有效目标信息[6],合理分配对于不同跟踪目标之间的数据率,是有效使用相控阵雷达信号能量的一个关键,同时合理的算法有利于节约雷达时间资源和降低对计算机处理能力的要求,而目前对低数据率下HRRP 序列的特征提取与识别缺少相关研究。
因此,本文以低数据率HRRP 序列为研究对象,研究进动特征提取方法以及联合多特征进行弹道中段目标识别。本文考虑目标的尺寸、形状和微运动模型等差异,仿真弹道导弹中段飞行场景中弹头、重诱饵、轻诱饵、碎片目标的特性数据,结合仿真数据,研究利用低数据率HRRP序列提取目标进动特征、结构特征,并利用随机森林方法对各类特征的重要性进行评估,应用多特征融合技术联合雷达目标的各类特征进行弹道目标识别,提升雷达目标的识别性能。
1 弹道中段目标特性分析
1.1 弹道中段目标运动特性
弹道导弹飞行包括助推段、中段、再入段。弹道导弹点火后,先在助推段以直线路径上升,导弹在此阶段的飞行时间较短,当达到预定高度后,则进入中段飞行阶段,此时弹头和弹体分离,弹头依靠惯性飞向目标,最后再次进入大气层向目标飞行的阶段为再入段。由于中段为反导系统提供识别目标的时间较长,若该段的弹头精准识别能提高整个反导系统的拦截概率。因此,中段目标识别是导弹防御系统的研究重点之一。
弹道中段目标主要包括弹头、诱饵和碎片等。利用图1(a)表示一个典型的锥形弹头在中段飞行过程中的进动模型,其运动可以看作两种类型的旋转运动的组合:自旋以及目标轴线围绕进动轴的锥旋,图1(b)利用方形柱体表示碎片的翻滚运动。为区分不同类型的微动,利用自旋频率ωz、进动频率ωp、翻转频率ωt和章动角θ参数对目标微动进行建模[7]。以图1(a)所示的进动模型为例,假设以目标质心O为原点建立参考坐标系XOYZ。目标围绕自身对称轴OA旋转的自旋角速度设为ωz,目标绕着进动轴OZ旋转的运动称为锥旋,目标锥旋角速度设为ωp,OZ与OA的夹角为θ,称为进动角。假设雷达视线(Radar Light of Sight,RLOS)方向位于平面内,YOZ与OZ的夹角α为雷达视线角,RLOS 与OA轴的夹角ρ称为姿态角。假设在t=0时刻,自旋轴在YOZ平面的初始方位角为φ0,则姿态角ρ随时间的变化公式为
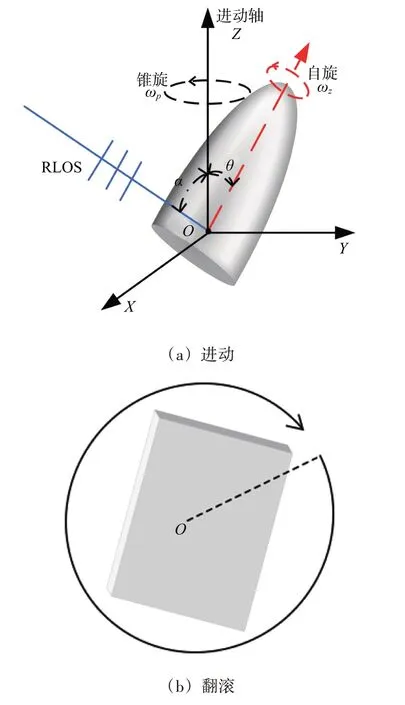
图1 弹道中段目标的运动模型
其中雷达视线角α会随着弹道目标飞行时间的推移而改变,弹道导弹中段的飞行时间一般为十几分钟,而进动周期为秒级,α在一个进动周期内的变化几乎可以忽略,所以α可看作固定值。进动角θ对姿态角ρ(t)的影响与α等效。当进动角确定时,姿态角ρ是随时间周期性变化的,从而可根据目标姿态角的改变来估计目标的进动周期。
利用公式(2)表示HRRP,其中f为频率,c为光速,k为目标上的散射点数,Bk和Rk分别是第k个散射点的幅值和第k个散射点与观测雷达的距离。
1.2 宽带雷达HRRP回波仿真
本文利用卫星工具箱(Systems Tool Kit,STK)模拟弹道导弹飞行,飞行轨迹如图2所示,图中粗体线显示部分为导弹飞行中段,宽带雷达在此阶段对目标进行观测,观测时长为280 s,仿真获得的雷达视线角范围在[55°~85°]。
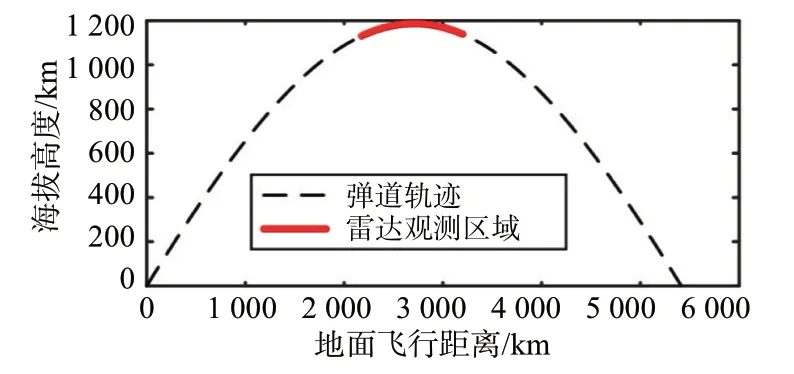
图2 仿真弹道导弹轨迹示意图
根据弹道中段的弹头和诱饵在运动过程中进动频率、翻滚频率、章动角的差异,仿真了弹头、重诱饵、轻诱饵和碎片4 种类别目标,并分别设置不同的尺寸类型(如图3所示)和不同的微动参数(如表1所示)。目标微动模型通过以下4 种参数确定:自旋频率ωz、进动频率ωp、翻滚频率ωt,以及进动角θ。
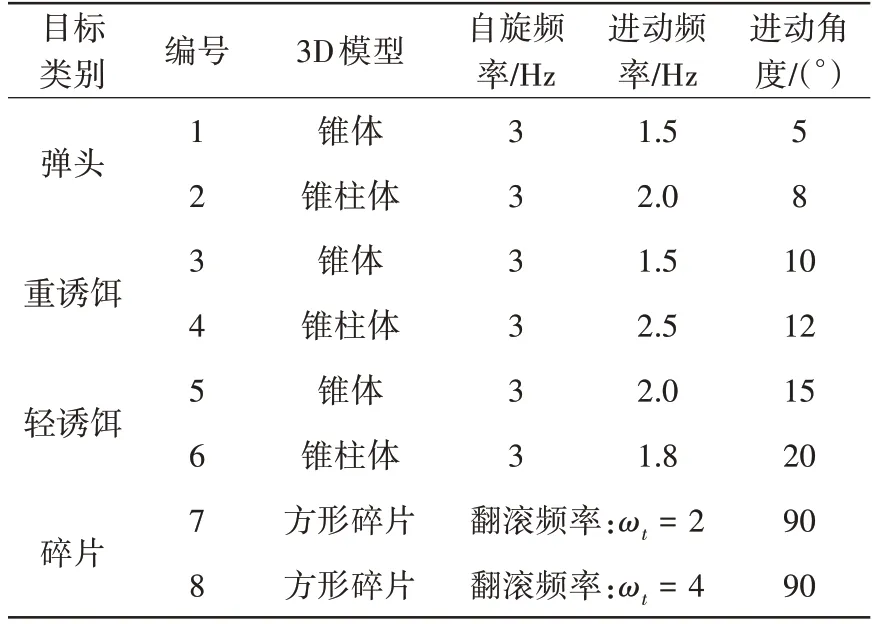
表1 仿真目标的微动参数

图3 3种典型模型示意图
将表1 设置的目标微动参数和STK 仿真获得的雷达视线角数据代入公式(1)中,可获得每个采样时刻的目标姿态角。利用目标姿态角,查找使用电磁散射仿真工具(FEldberech-nung bei Körpern mit beliebiger Oberfläch,FEKO)仿真获得的雷达散射幅度和相位,再将STK 仿真的导弹轨迹信息(距离、速度)、目标姿态时间序列和对应的电磁计算结果联合获得宽带回波信号[8]。最后,将高斯白噪声与理论雷达回波信号叠加,得到雷达观测回波信号。观测区域目标飞行时长共280 s,在此范围内,使用1 s 窗长将雷达的回波信号切片以形成280 个窗口信号,采用4∶1 比例将280 个信号窗口进行随机划分,获得224 个信号窗口作为训练集,其余56 个信号窗口用于测试集,每个信号窗口中均包含表1所示的8个类别的样本。
2 低数据率下HRRP进动频率特征提取方法
为了使远程雷达发射的脉冲有足够的辐射能量来获取有效目标信息,对应地就需要降低雷达脉冲重复频率,而进动频率又是识别运动弹头目标的关键性特征,因此本节研究对低数据率HRRP序列进行频率特征提取方法。
以图1的锥柱体模型作为实验对象进行分析,选用表1 中编号为2 的锥柱体目标,具体参数如表1所示。假设宽带雷达发射频率步进信号,将雷达中心频率f0设置为9.5 GHz,频率步长Δf设置为15.625 MHz,频率步进数N设置为64。取雷达视线角为50°时,雷达脉冲重复频率(Pulse Repetition Frequency,PRF)分别为500,200,50 和10 Hz 的雷达回波HRRP 序列,取HRRP 序列的第32 个散射单元进行短时傅里叶变换(Short Time Fourier Transform,STFT),获得图4 的时频图。可以看到PRF 为500 Hz 的时频图中有明显近似于正弦振荡的时频曲线,在PRF 为200 Hz和50 Hz时时频曲线特征削弱,但回波产生的HRRP序列的时频曲线仍具有明显的周期特征。以往研究中对散射点的时频曲线进行拟合,再求出震荡频率,从而估计出目标的频率特征,但是这类直观的进动频率估计方法只适用于高重频。当PRF 值过低(10 Hz 以下),时频曲线会出现严重的频域模糊和交叠现象,从而导致从时频图中提取出时频脊线的方法会变得复杂,但通过观察时频分布图4(d)可以发现,强散射中心的能量强弱在时域呈现出周期性变化,依据此特性,本文通过将能量在时间轴上进行竖投影,可以将能量强弱在时频图上的分布特征变成一维特征,如图5(a)所示。

图4 不同PRF值下的时频图
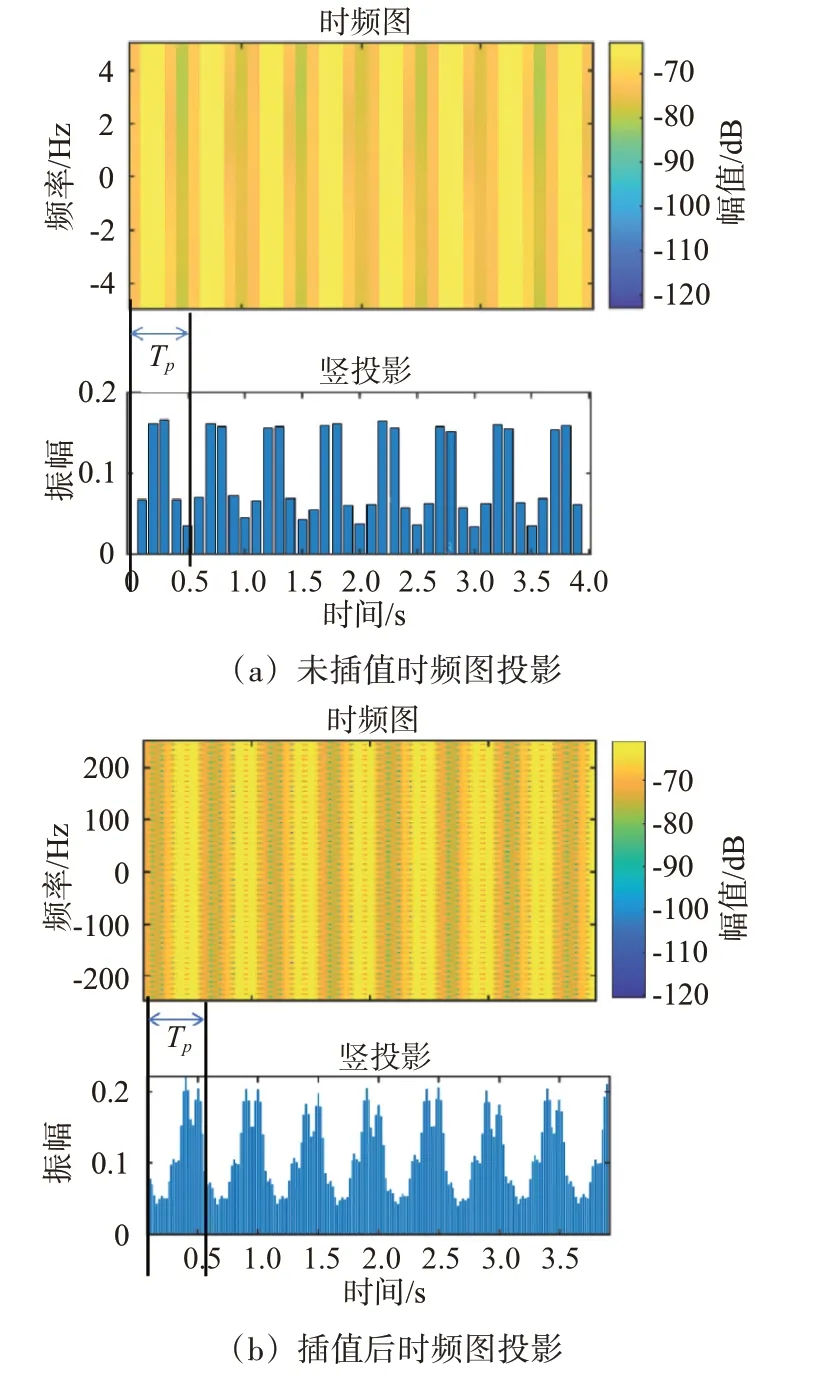
图5 时频图一维投影曲线对比(PRF=10 Hz)
对图4(d)中PRF 为10 Hz 时的时频图进行投影,结果如图5所示,图5(a)为进行时频投影后的曲线,振幅代表投影后能量强弱分布。由于在进行竖投影时原采样率低,导致幅度在时间轴上呈现的周期性特征仍不够明显和精确,因此对HRRP序列在慢时间域进行插值,插值后的采样率为500 Hz,此时竖投影后的效果如图5(b)所示。经插值再投影后的幅度强弱在时间轴上呈现出更加明显的正弦周期性变化,竖投影序列的幅频图如图6所示,可以得到其峰值处的频率为2.050 8 Hz,与真实值2 Hz误差较小,说明该一维曲线的震荡频率与目标的进动频率接近,可作为目标进动频率的估计值。
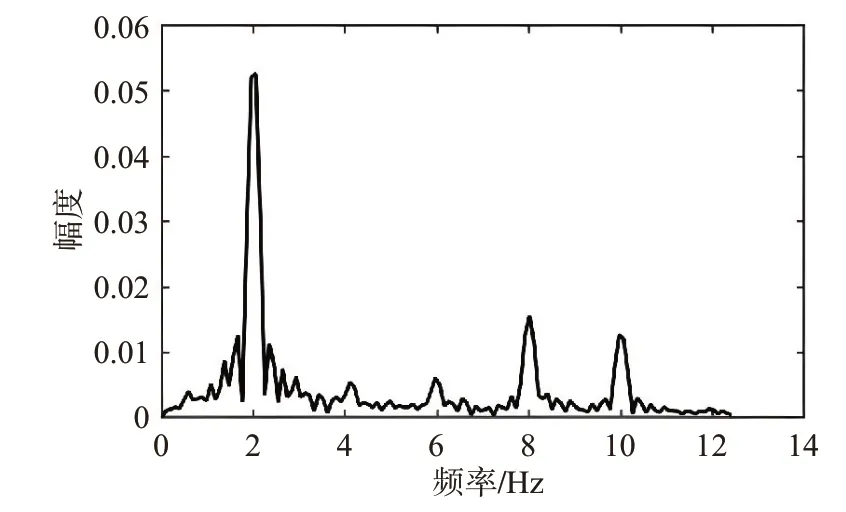
图6 竖投影序列的幅频图
低数据率HRRP 序列下进动频率特征提取算法步骤如下:
步骤1:首先对接收到的Np帧目标HRRP 进行进动周期提取,其中每幅距离像内距离单元数为Ns,则建立待处理一维像数据矩阵为
式中Ns代表每幅距离像内的距离单元数,Np代表接收到的目标HRRP帧数。
步骤2:对Np帧HRRP 序列在慢时间域进行补零插值,获得矩阵H1MNp×Ns,假设原HRRP 序列的采样率为fs,补零插值为M,插值后的采样率为fd且有以下关系:
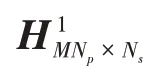

式中fi=i⋅Δf,Δf代表采样频率间隔。假设从HRRP 序列中提取出Nsk个强散射中心单元,对每个强散射中心单元重复步骤3、步骤4,获得Nsk个进动频率估计值,对其求均值,得到最终的频率估计值。
3 基于多特征融合的弹道中段目标识别
上节提出了低数据率HRRP 序列的进动频率特征提取方法,但由于轻、重诱饵与弹头存在相似的进动特性,因此还需要提取多个目标特征联合对目标识别,提升低数据率HRRP序列下目标识别准确率。本文对低数据率HRRP 序列提取了目标结构特征、熵特征和周期特征等,各特征具体计算方法如表2所示。
多特征级融合是指在融合前传感器对原始数据进行特征提取,产生特征向量并进行关联,再利用分类器进行分类识别[9]。本文基于低数据率HRRP 序列与特征级融合方法对弹道中段目标分类和识别整体方案如图7所示。整体分为训练和测试两大模块,训练部分包括4 个步骤:1)目标信号获取 将通过雷达传感器观测目标获得的HRRP 序列作为样本数据输入待训练模型;2)特征提取 对信号提取稳定、可分性高、易于提取的特征,包括目标结构特征和进动频率特征;3)信号特征融合处理 采用拼接方式将传感器测得的信号特征融合为长向量;4)特征分类 采用随机森林分类算法对特征进行分类,获得待识别目标的类别并输出最终融合结果。测试部分通过对HRRP 样本测试数据基于特征重要性分析投入到分类器中,根据训练结果进行分类识别,最终输出结果。
4 实验与分析
4.1 进动频率提取算法性能分析
为分析低数据率下HRRP 序列的进动频率提取方法性能,考虑回波统计窗长为2~7 s,PRF 为10~100 Hz,间隔为1 Hz 的情况下,对本文所提方法与文献[5]所使用的广义Radon方法的进动频率提取性能进行比较。为保证结果的可靠性,本文进行50 次蒙特卡洛实验,得到的估计均值分别如图8所示。可以看出本文方法下当回波统计窗长为2 s,PRF 值为10 Hz 附近时,进动频率估计均值在2 Hz 上下有微小浮动;当回波统计窗长达到4 s时,估计值结果相较于窗长为2 s时更为稳定,几乎无浮动,因此准确率更高。而广义Radon法在低数据率下准确率低,曲线有明显波动。从实验结果可以看出窗长为4 s时即可达到理想效果。可以看出本文算法相较于广义Radon 法误差值更低且更稳定。通过实验结果对比可得,文献[5]的基于广义Radon 变换方法在低数据率和多散射点的情况下,对频率值的估计会产生较大偏差,而本文所提出的方法在低数据率和复杂模型下具有更好的估计准确性和稳定性,因此在低PRF 下采用本文方法估计频率更具优势。因此综合考虑时间成本及测试效果,本文选取回波统计窗长为4 s,PRF 为10 Hz时进行后续分类识别实验。

图8 算法在不同数据长度下的进动频率估计均值
4.2 特征重要度分析
在弹道中段目标识别中,分类器的选择至关重要。常用的分类器有:kNN、朴素贝叶斯、集成学习法中的Bagging 算法、随机森林等。不同的分类器适用于不同类型和容量的样本,k 邻近属于无监督学习,更适用于样本容量适中、相似度较低、代表性强的场景,如区分碎片、轻诱饵和弹头,当样本容量不平衡或者相似度很高、代表性弱化时,误差较大,如区分重诱饵和弹头;集成算法在多诱饵干扰场景下由于其模型的集成泛化能力更强,因此方法的稳定性能优于kNN。而随机森林是在Bagging 算法基础上,选择决策树作为基学习器,除了具有Bagging 随机样本还包含了随机样本特征,提高了泛化能力。将表2 中的特征融合成特征向量,输入kNN、Bagging、随机森林分类器,获得的各目标分类结果如表3所示,结果随机森林法效果拥有更好的识别性能,对真弹头的识别率达到95.3%。

表3 各目标在不同分类算法下的识别准确率%
一个数据集中往往包含很多特征,从中选择对结果影响最大的几个特征,以此提升存储与识别的性能也是十分重要的问题。因此在这一步中本文基于特征重要性评估来进行特征选择[10],其思想是根据不同特征在数据森林中每个决策树上的贡献度先选取合适的特征子集,按照各个特征的重要性度量将特征重要性依次排序,再对每个特征进行遍历搜索,在每次迭代过程中从特征子集中删除一个重要性低的特征,逐次进行,最终选取分类精度最高的对应的特征作为选取结果。各个特征的重要性排序情况如图9所示。
参数f1~f10所对应的特征类别如表2所示,图9为特征重要性从高到低排序结果,依次代表进动频率、散射点数、目标长度、偏度、不规则度、目标长度周期、SVD、熵值、长度变化幅度、回波功率。从图中可以看出本文所提取的进动频率重要程度最高,而锥体结构上的散射点数特征重要程度次高,有效证明了进动频率特征的提取对于目标识别的重要性。
4.3 多特征融合的弹道中段目标识别
根据图9对各特征的重要性排序结果,将不同目标特征构成10个特征子集分别对弹头目标进行识别,各目标在不同特征级融合方法下的识别准确率如表4所示。由表4 可以看出,仅利用进动频率特征时,识别准确率为68.33%,识别效果不佳。随着特征子集中特征数量的增加,目标的识别准确率呈现出逐步上升的趋势,当特征数量达到6个时,此时特征集合为{进动频率、散射点数、目标长度、偏度、不规则度、目标长度周期},准确率达到96%并趋于稳定。

表4 各目标在不同特征级融合方法下的识别准确率
5 结束语
本文通过分析中段弹道的锥柱体模型,结合仿真数据研究,提出了低数据率下HRRP序列的目标进动特征提取方法,再利用多特征融合技术联合目标运动、结构等特征进行弹道目标识别,提升雷达目标的识别性能。首先,对不同数据率HRRP序列的时频图进行分析,提出了利用时频投影法的进动频率特征提取算法,该算法能够在低PRF范围(10~100 Hz)时对进动频率的提取具有高准确性和稳定性,误差值小于0.05 Hz;其次,提取多个目标结构、熵等特征,利用随机森林对目标多特征进行重要性分析,给出不同数量的特征子集下的识别效果,通过实验分析可知,当联合进动频率、散射点数、目标长度、偏度、不规则度、目标长度周期时,准确率在96%并趋于稳定。
对于低数据率HRRP的弹道中段目标识别,本文方法达到了节约宽带雷达资源的目的,同时获得了较好的识别结果。在多目标跟踪情况下,按目标重要性或威胁度可以有不同的跟踪采样间隔时间,这些情况使得数据率这一指标在相控阵雷达信号资源分配和工作方式安排与控制中起着十分重要的作用,因此基于本文的工作,接下来将研究弹道中段目标识别系统的资源调度方法,能够根据雷达系统的技术特点、探测任务、目标特性及电磁环境等条件,合理调度时间和能量等有限资源,提升识别资源利用效率。
