基于质点模型的船用空压机振动诊断与分析
2023-10-31蔡晓涛黄志武
刘 金,张 浩,蔡晓涛,方 正,黄志武
(1.江南造船(集团)有限责任公司,上海 201913;2.中国船舶集团有限公司第七一一研究所,上海 201108)
0 引言
随着造船事业的蓬勃发展,现代船舶向绿色、智能、安全、舒适性方向发展,对船用机械设备的性能要求愈加重视。空压机作为关键的船用设备,是一些工程船、公务船和港作船舶的重要动力装置,由于科考船、物探船、客滚船等船舶对振动噪声的严苛要求,使得对船用空压机等机械设备的振动噪声控制也具有较高的要求。
针对空压机的振动噪声控制,国内学者进行了诸多研究。朱宝庆等[1]分析了船用立式高压空压机的振动机理,通过对比分析和改进试验实现了空压机与隔振装置的最佳控制效果。刘雁等[2]研究得出压缩机出口动态压力的最大Lyapunov指数特征能够实现离心压缩机的初始喘振识别和预测以及控制。为避免往复式压缩机曲轴系出现扭振,陈振等[3]建立了曲轴系在全周期交变载荷作用下的动力学模型,得到了曲轴系的固有频率以及振型,通过分析曲轴系在不同转速点的耦合振动速度响应规律,提高了压缩机曲轴系的使用寿命和工作可靠性。戚蒿等[4]采用平面波动理论和转移矩阵法,对空压机系统进行优化设计,能够有效地避免空压机管道系统在不同操作工况下的气柱和管路机械共振问题。针对空压机振动故障的分析和振动控制,李树勋等[5]基于ANSYS有限元分析软件,对振动剧烈的管路进行流体压力脉动计算和流固耦合模态分析,得出空压机管路振动是流体压力脉动频率和管道机械固有频率均落在了压缩机激振频率共振区内,通过增加防振管托在一定程度上减弱了管道振动。黄辉等[6]着重探讨了造成压缩机切向振动和径向振动的原因,并针对性地提出动平衡优化、排气口优化、转动惯量优化等压缩机振动的控制方法。倪天智等[7]搭建一种自适应窄带陷波滤波器的主动减振系统,并首次用于压缩机减振,能够将压缩机基频振动减小21.2 dB。
综上所述,船用空压机的减振设计和振动控制一直是机械领域研究中需要持续关注和解决的问题,而基于质点模型的船用空压机隔振装置系统的振动故障识别方法研究而言,相关研究成果较少,国内外对空压机与隔振装置的振动分析也通常是将两者分开单独考虑,很少对隔振系统整体特性进行研究。因此,本文针对某船用空压机隔振装置系统出现的振动问题,建立质点有限元模型进行仿真验证,得出空压机基频激励引起了系统的共振。提出通过更改隔振器刚度的方式进行优化,并得到实船测试证明,该空压机振动问题成功解决,为船舶安全作业提供了可靠保障。该研究可为船用机械设备出现异常振动时的判断、识别以及治理提供十分有益的参考。
1 空压机基本参数及振动现象
通过上船勘验,该空压机组采用单层隔振的方式弹性安装在船体基座上,每台空压机安装6个隔振器,如图1所示。其中,技术图纸中空压机组隔振装置的隔振效果不小于10 dB(10 ~10 kHz频带范围内),空压机参数见表1。
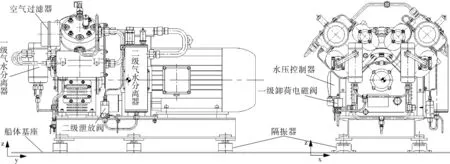
图1 空压机布置Fig.1 Air compressor layout
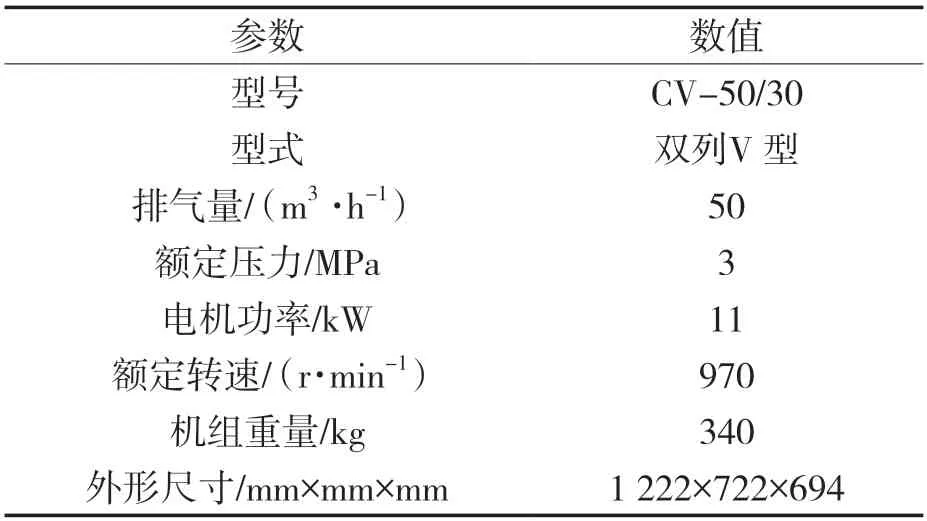
表1 空压机参数Tab.1 Parameters of air compressor
在系泊调试阶段发现,当空压机达到额定转速970 r/min时,整个机组出现明显异常振动,机组振动幅度远远大于机舱内的其他机械设备,并且强烈的振动引起空压机摔油杆断裂。
2 实船振动测量与分析
2.1 测试设备及测点布置
为了明确机组振动的原因,采用振动测量的试验方法对其进行振动信号的采集。测试系统主要有单向加速度计(丹麦B&K,4514-B-001),信号采集分析系统(丹麦B&K,3050-A-060),安装有PULSE软件的测试电脑等组成。分别测量空压机的机脚振动加速度,测量参数为1/3倍频程振动加速度级,频率范围为10 Hz~10 kHz;并测量机组隔振装置的隔振效果,测量参数为机组机脚至船体安装基座的平均加速度振级落差,频率范围为10 Hz~10 kHz。测量参考值为1 mm/s2,频率分辨率为1 Hz。
振动测点为空压机组的机脚以及靠近隔振器的船体基座,加速度传感器通过螺纹连接在金属座上并通过粘接剂安装在机组各测点。布置测点时注意避开结构局部振动过大的部位(如罩壳、薄板、悬臂等),测试结果中振动加速度振幅均为所测频段内的有效值。
2.2 振动测试及分析
通过对空压机组的振动测试,机脚振动加速度级1/3倍频程如图2所示,振动加速度级垂向为144 dB、船宽方向为143 dB、船长方向为148 dB;振动速度线谱结果如图3所示:振动速度总值在船宽方向为61.3 mm/s、船长方向为28.4 mm/s、垂向为33.5 mm/s。振动烈度远超GB/T 7184-2008的C级要求(小于28.2 mm/s),此状态继续工作会对空压机造成严重的损坏。
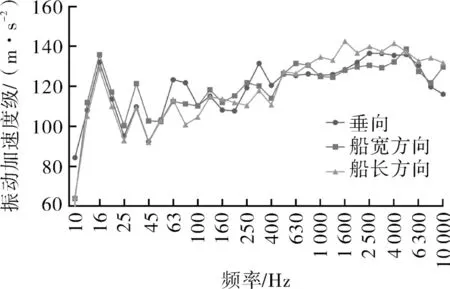
图2 机脚振动加速度级(1/3倍频程)Fig.2 The vibration acceleration level of the machine foot(1/3 octave chart)

图3 机脚振动速度(线谱)Fig.3 The vibration velocity of the machine foot(line profile)
分析频谱可知,船宽方向振动最大,垂向振动次之,船长方向振动最小。从图2,3可知,各测点数据中振动能量最大的频率均为16 Hz,对应空压机的基频,并且远远大于其他响应频率,说明空压机发生了基频振动异常故障。
对空压机组隔振装置的隔振效果进行了测试,其结果如图4所示。在10 Hz~10 kHz频段的隔振效果为24 dB,远大于指标要求的10 dB。表明隔振装置具有较好地减少振动传递的效果,在减振设计上留有较大的裕量。
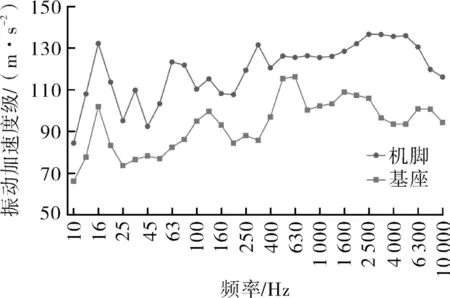
图4 空压机隔振效果曲线(1/3倍频程)Fig.4 Vibration isolation effect curve of air compressor(1/3 octave chart)
往复式机械设备出现基频振动异常的故障,往往存在以下几种原因:(1)对中不满足要求,存在角度不对中、平行不对中或综合不对中;(2)机械设备的机脚紧固螺栓出现松动;(3)设备弹性安装时,设备和隔振装置组成的系统发生共振。
针对以上3种可能,逐一进行确认。
(1)通过现场检查测量,该空压机对中状态良好。
(2)通过复查空压机与隔振器连接螺栓,隔振器与船体基座连接螺栓,均未出现松动现象,且螺栓扭矩均在标准范围之内。
(3)验证系统是否存在共振。
由于该空压机组采用单层隔振方式进行弹性安装,因此需要验证整个机组系统是否存在共振。
3 质点模型的有限元分析
3.1 质点模型的建立
考虑到数值模拟结果对实船空压机系统模态计算的准确性,本文基于质点模型进行有限元分析。质点是物理上描述物体运动时建立的一种理想化模型,是一个具有质量的点,它的质量等于物体的全部质量,但体积为零。杨辉等[8]为减少重载列车因制动延时导致的纵向冲动,将列车的每节车辆作为一个质点,建立重载列车多质点动力学模型,试验结果与质点模型的仿真结果相吻合。王志斌等[9]针对多分支电缆的柔性特征以及复杂拓扑结构导致的装配仿真困难的问题,提出一种面向电缆虚拟装配仿真的多分支弹簧质点模型,能够满足柔性电缆碰撞检测的效率和精度要求[9-12]。
针对空压机组系统是否存在共振,利用有限元分析软件,建立质点模型,采用0维MASS单元将船用空压机等效为一个质点,并在这个质点上赋予机组重量和转动惯量等信息,质点位置为机组的重心位置。机组转动惯量JX=15 195 T·mm2,JY=30 361 T·mm2,JZ=29 686 T·mm2。隔振器采用SPRING弹簧单元,根据设计图纸可知,本船空压机所使用的隔振器为BE-85型,该隔振器单个承载为50 kg,动刚度x向(船宽方向,记为横向)为600 N/mm,y向(船长方向,记为纵向)为230 N/mm,z向(垂向)为250 N/mm。将空压机质点与隔振器单元通过MPC点RBE2单元进行约束,实现节点自由度耦合,如图5所示。考虑到隔振器通过螺栓与船体基座相连接,对隔振器单元节点底面的平动和转动方向施加全约束,进行模态分析。
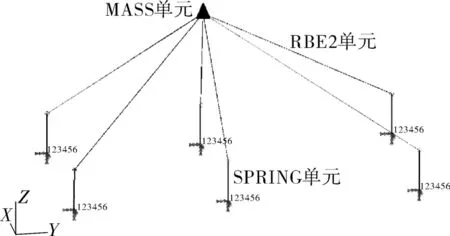
图5 空压机组系统质点模型Fig.5 Particle model of air compressor system
3.2 空压机系统模态分析
系统前6阶模态频率计算结果见表2。根据空压机隔振系统运行时的机脚振动测试结果可知,空压机在额定转速970 r/min时,振动的峰峰值对应的中心频率为16 Hz,结合线谱可知该频率为空压机的基频(970 r/min对应激励频率为16.17 Hz),与系统第4阶频率15.55 Hz吻合。可以认为该机组弹性安装后发生的基频振动异常故障的原因是系统存在共振所导致的。

表2 系统模态计算结果(原始隔振器刚度)Tab.2 Calculation results of system modal(Stiffness of original vibration isolator)
结构共振问题导致发生振动故障一般需要满足2个条件,首先结构的模态频率与激励频率吻合;其次,激励源在该频率下能够提供足够的能量输入。根据线谱和1/3倍频程谱可知,在16 Hz及其倍频处均出现峰值,并且基频响应较为突出,因此基频提供了足够的能量贡献造成整个系统出现共振。
由于隔振器与船体基座刚性连接,船体基座已有较大的刚度,改变船厂基座刚度并不能较好地改变整个系统的频率,因此改变隔振器刚度能够避免系统固有频率与空压机基频吻合,有效减弱空压机的振动。通过对隔振装置的隔振效果测试可知,该机组使用的隔振器刚度太弱,因此有足够的裕量可以在满足隔振效果的同时,提高刚度来避开共振频率。
3.3 系统模态验证
通过定量化设计,改变隔振器橡胶胶料来改变隔振器刚度,计算中应考虑10%的共振带范围,系统模态需要避开14.5~17.8 Hz共振带。隔振器动刚度x向取2 260 N/mm,y向取820 N/mm,z向取800 N/mm。通过质点模型计算得出系统前6阶模态频率结果见表3。根据模态计算结果得到其2阶模态频率提高至14.01 Hz,3阶至19.16 Hz,可以看出该隔振器刚度能够使空压机系统避开基频16.17 Hz,减少空压机组的振动。

表3 系统模态计算结果(定制隔振器刚度)Tab.3 Calculation results of system modal(Stiffness of customized vibration isolator)
4 隔振器更换后实船振动测试
按照上文相同设置和测点布置,对空压机组进行振动复测,机组振动得到有效改善,测试结果如图6-7所示。振动速度总值在船宽方向为22.7 mm/s、船长方向为19.3 mm/s、垂向为26.2 mm/s,且振动线谱中16 Hz处振动幅值明显降低,无异常,系统共振现象已消除。说明通过改变隔振器刚度,改变了系统的固有频率,避免了在空压机额定转速激励下的共振现象。更换隔振器后,隔振装置的隔振效果为15.0 dB,满足指标要求。
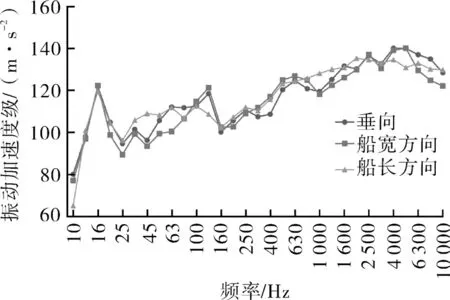
图6 机脚振动加速度级(1/3倍频程)Fig.6 The vibration acceleration level of the machine foot(1/3 octave chart)
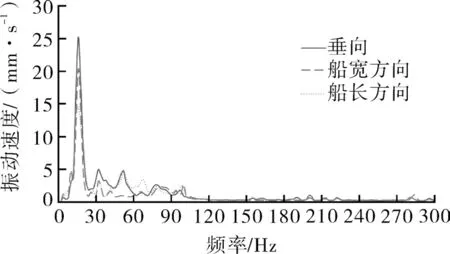
图7 机脚振动速度(线谱)Fig.7 The vibration velocity of the machine foot(line profile)
5 结论与建议
本文通过采用有限元分析软件建立质点模型以及实船空压机振动测试,对空压机出现的振动问题进行分析,研究振动控制措施在该空压机产生振动前后的控制效果,主要结论如下:
(1)对空压机设备进行振动测试,得到了设备实际振动响应数值和方向,振动的主要频率为空压机的基频。
(2)通过建立空压机质点有限元模型进一步确认系统的固有频率与空压机基频吻合,导致发生了共振。
(3)针对性地提出振动控制措施,通过改变隔振器刚度进而改变系统固有频率,并进行质点模型仿真计算和实船振动测试验证。空压机额定转速下振动速度发生明显的降幅,振动处于正常水平,证明空压机的振动问题得到有效解决。
(4)当机械设备出现异常振动时,利用质点模型进行有限元仿真,可以快速确认故障特征,进而制定有效控制方案,解决设备的安全隐患。
以上研究结果为船舶动力设备的设计和船舶振动故障的判断、识别以及治理提供了宝贵的经验,具有较好的借鉴意义。
