基于Arrhenius公式的电缆附件硅橡胶寿命预测模型

2023-10-31朱卫东

绝缘材料 2023年10期

朱卫东，谢庆

（华北电力大学电力工程系，河北保定 071003）

0 引言

在电缆接头及终端处安装电缆附件，可通过附件结构改变物理场分布，使得电缆中间接头及终端连接处的各项电气参数满足安全需求[1-2]。但电缆本体的交联聚乙烯（XLPE）与电缆附件的硅橡胶（SiR）之间会形成复合界面，这一特殊的结构使得电缆附件成为电力输电系统中最薄弱的环节和运行故障的典型部位[3-6]。

冷缩附件使用的冷缩管在使用前是被塑料芯绳撑开的状态，内径大于电缆本体，而其自然状态下，内径小于电缆本体[7]。由于SiR材料的弹性形变特性，电缆附件在安装后会在界面形成一定的“抱握力”，即界面压力[8]。界面压力的存在是确保电缆附件长期安全可靠运行的关键[9]。张静等[9]采用内置传感器法对长期热老化电缆附件的界面压力松弛特性进行了研究，结果表明随老化时间的增加与老化温度的升高，电缆附件的SiR 材料会产生不可恢复形变，从而使得界面压力降低，界面密封性能变差，进而影响SiR 附件的使用寿命。但该研究在压力测量环节未对压力传感器进行校准，试验结果在一定程度上无法反映真实的界面压力变化规律。王霞等[10]从高压电缆附件的设计角度出发，给出了当前电缆附件工艺设计上的一些建议，认为运行温度越高，SiR 材料的伸长率越大，应力松弛越快，附件的使用寿命下降越明显。包淑珍等[11]基于橡胶本构模型的超弹性力学理论，利用有限元分析软件COMSOL建立了电缆接头的二维轴对称仿真模型，研究了在不同温度下，不同运行年限电缆XLPE 绝缘弹性模量变化对界面压力的影响，获取了接头轴线上的界面压力分布情况。王子康等[12]研究了电缆长期处于冷热循环状态时附件界面压力的变化规律，结果表明SiR 材料特有的弛豫特性会导致附件的界面压力先增大后减少，但即便是在50个周期的高温热循环老化后，界面压力仍满足运行要求。

我国对于冷缩附件的应用起步较晚，相关研究也大多数集中在理论层面，相关标准的制定也仍旧处于摸索阶段。然而，随着电缆投运时间的增加，近几年电缆附件事故频发，其中很大一部分原因是长期处于运行状态下的SiR 材料力学性能下降[13]。为此，本研究对某主流电缆附件进行加速热老化，对热老化后SiR 的材料特性和热失重特性进行测试，并利用Arrhenius 公式基于SiR 的断裂伸长保留率构建其寿命模型。

1 试验

1.1 试验对象

目前工业用硅橡胶材料主要是由聚二甲基乙烯基硅氧烷与氢基硅氧烷在催化剂的作用下发生加成反应，生成的以Si-O键为主链的聚二甲基硅氧烷（PDMS），并在此基础上添加一定量的白炭黑（SiO2）和Al(OH)3填料用以对材料进行机械强度补强[14]。本研究选取当前某主流10 kV 电缆附件，该附件套管材料与附件主体材料组分完全一致，套管各处的厚度一致，因此为保证试样的受热分布一致且便于后续力学性能测试以及对材料进行切样采集，试验均选取该厂家生产的同一批次套管进行相关试验。

1.2 热老化试验与试样采集

将套管的支撑条抽离，并安装在处理好后的短电缆试样上。将制作好的短电缆样本放置于烘箱中进行加速热老化，由于电缆主绝缘XLPE 材料的熔点在130℃左右[12]，为避免不必要的绝缘损伤对试验结果造成影响，老化温度选择为120℃。参考文献[12]的试验方案，对试样进行共计1200 h 的老化处理，每隔240 h 进行一次采样，每次采样时选取距离端部总长度1/6 的位置进行切向环切，以保证在后续制作哑铃状试样时，切割样本有足够的宽度，总共得到6组不同老化时间的样本。

1.3 拉伸性能测试

杨氏模量和断裂伸长率是构建SiR 材料老化寿命模型的关键参数[15]。使用SGH-A102 型万能材料试验机对老化后的试样进行力学性能测试，测试中使用位移控制模式，并设置加载应变率为0.001 s-1。使用万能试验机上的夹头来固定平板状试样，从而尽量避免由于试样在测试中滑动所带来的结果误差。拉伸试验在室温条件下进行，测试时将试样裁剪为标准哑铃状，其中拉伸有效长度为10 mm，拉伸速度为50 mm/min。取从中间断裂而非压口处断裂的试样为有效试样，每组有效试样不少于3片，记录试样的杨氏模量与断裂伸长率，结果取平均值。

1.4 热重-差示扫描量热（TG-DSC）测试

通过Arrhenius公式预测材料的寿命时，根据反应动力学原理，需要获取材料的活化能，因此本研究采用STA449F3 型同步热分析仪对套管用SiR 材料进行测试。该仪器能够同时生成TG 曲线和DSC曲线，仪器可测试的温度范围为-120～1650℃。对于DSC 测试而言，升温速率越快，分辨率越低，灵敏度越高。反之，分辨率越高，灵敏度越低，测试时的升温速率通常建议控制在5～20℃/min。本研究的升温速率β选取为5℃/min和10℃/min。

2 试验结果

2.1 拉伸性能试验结果

未老化及老化SiR 材料试样的拉伸测试结果如图1 所示。由图1 可以看出，随着老化时间的增加，SiR 材料的弹性模量整体呈现增大的趋势，而断裂伸长率和拉伸强度整体逐渐减小。此外，可以直观感受到老化时间越长的SiR 材料越硬。上述现象表明，热老化过程中，SiR 材料的力学性能发生了较大的变化，这可能是由于热老化过程中材料内部分子发生了交联和热降解等化学反应[16]。

图1 老化过程中SiR材料的力学参数变化Fig.1 Changes of mechanical parameters of SiR materials during the ageing process

2.2 TG-DSC测试结果

对全新的SiR 材料进行TG-DSC 测试（β=10℃/min），结果如图2 所示。由图2 可以看出，SiR 材料的热失重曲线基本符合工业用硅橡胶的特性，对于工业常用硅橡胶而言，其主要成分包含硅氧烷基胶、Al(OH)3和白炭黑，其中Al(OH)3的热分解温度为250～350℃，硅氧烷基胶的分解温度大于350℃，而白炭黑最为稳定，在极高温下也不会分解，因此图2 中SiR 试样的TG 曲线上出现两个平台，分别在0～240℃和380～410℃，而在两个平台以外的快速下降曲线则分别对应Al(OH)3和硅氧烷基胶的分解过程。

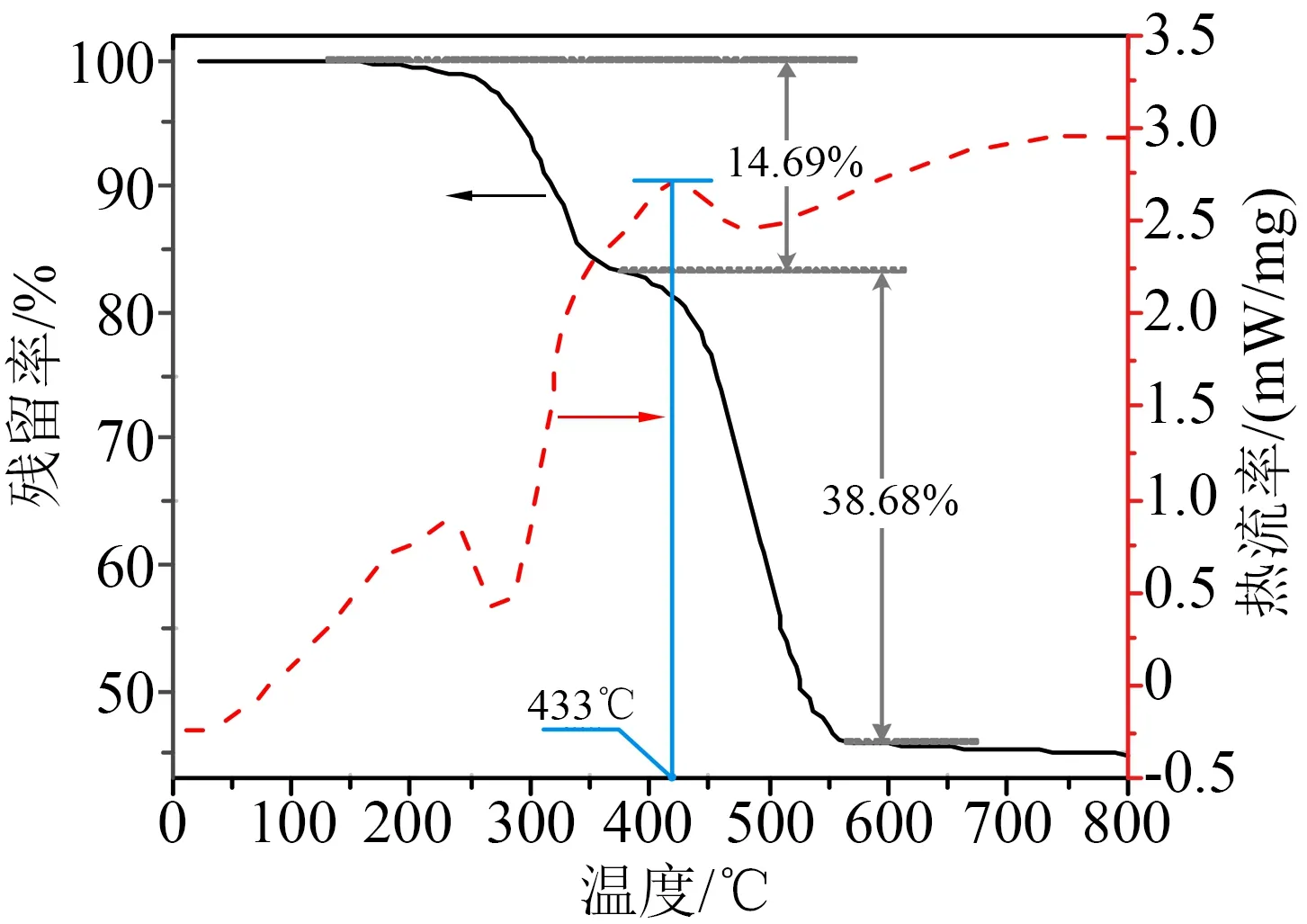
图2 SiR材料的TG-DSC测试结果Fig.2 TG-DSC test results of SiR material

DSC 一般用以测量升温过程中的焓变，在有机材料的分解过程中，一定会伴随着分子链段的解排与化学键的断裂，而活化能就用以定义反应物分子从稳定态到活化态所需要吸收的能量。图2 中SiR试样的DSC 曲线具有两个明显的放热峰，表明SiR在升温过程中发生了两次相态变化（固-固变化、熔融-结晶变化等），每次相态变化对应温度下的热效应发生最快[17-18]。从图2 可看出，当升温速率为10℃/min时，热效应发生最快的温度为433℃。

3 分析与讨论

3.1 基于力学特性分析的SiR热寿命分析

首先计算材料的断裂伸长保留率，计算公式如式（1）～（3）所示。

式（1）～（3）中：K表示断裂伸长保留率；K'表示老化后试样的断裂伸长率；K0表示试样的初始断裂伸长率；L0表示初始试样的标线间距，10 mm；ΔL'表示老化后试样断裂前标线间距变化值；ΔL表示试样断裂前标线间距的变化值。

不同热老化时间SiR 试样的断裂伸长保留率整理如表1所示。

以SiR 材料的老化时间作为横坐标，以平均断裂伸长保留率作为纵坐标并将散点图拟合成多项式，分别利用一次、二次和三次函数对上述数据进行拟合，发现三者的RMSE（标准误差）分别为0.583 8、0.664 9 和0.699 8，RMSE 越小，拟合精准度越高，因此采用一次函数进行拟合，结果如图3所示。

图3 SiR老化时间与断裂伸长保留率的拟合曲线Fig.3 Fitting curve of ageing time and breaking elongation retention rate of SiR

根据上述拟合曲线，将断裂伸长保留率分别为40%、50%、60%、70%和80%时作为其寿命终点，得到SiR材料的热老化寿命如表2所示。

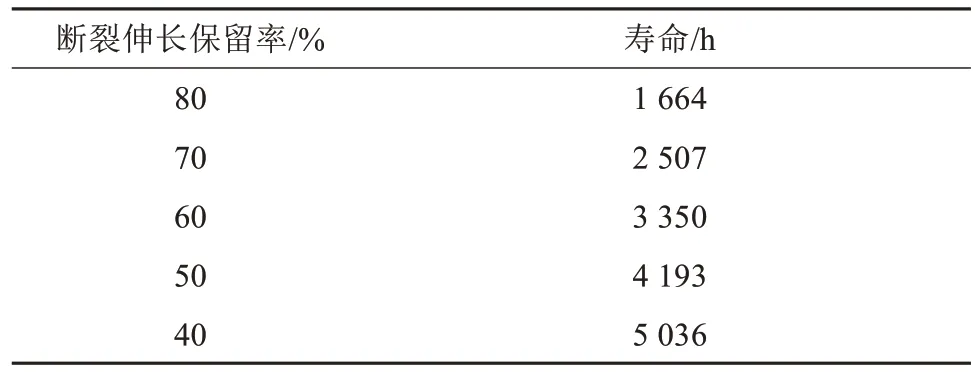
表2 以不同的断裂伸长保留率为寿命终点时，SiR材料的预计寿命Tab.2 Predicted life of SiR material with different breaking elongation retention rate as life end

3.2 基于Arrhenius公式的SiR热寿命分析

在化学反应动力学中，由反应速率方程及Arrhenius 方程，可得到高分子聚合物材料的热老化方程，如式（4）所示。

式（4）中：τ为材料的寿命；T为老化温度；a为与规定失效性能有关的常数；b=0.401×E/R，是与活化能E相关的常数，其中R为气体常数，其值为8.314 J/(mol·K)。

由式（4）可知，如果给定了材料的性能失效标准，则材料寿命的对数与材料所处环境的绝对温度的倒数成线性关系。因此如果能求出活化能E，就能确定直线上的斜率b；通过一个温度点下的加速热老化试验，可以确定直线上的一个点坐标，从而确定材料的热老化方程。

活化能可基于Arrhenius反应动力学进行推算，其原理如下：物质分子从稳定态跃升至活化态需要吸收或释放能量，亦即需要分子的热力学能发生改变（焓变），而DSC 采用动态零位平衡原理，即要求无论是吸热还是放热，试样与参比物的温度都要维持动态零位平衡状态，保持试样和参比物的温度差趋向于零。DSC 测定的是维持试样和参比物处于相同温度所需要的能量差（ΔW=dH/dt），反映了样品焓的变化。最终即可通过动力反应方程将焓变与活化能构建起联系[17]。

根据反应动力学原理，可以得到式（5）[19]。

对式（5）两边进行积分，可以转化为式（6）。

式（6）中：Tmax表示绝对温度；β表示升温速率；R和C分别表示气体常数与普通常数。

由式（6）可知，ln(β/T2max)与1/Tmax为线性关系，-E/R为其斜率。此时根据DSC 曲线在尖峰时对应的温度和升温速率，便可计算出相应的反应活化能。

对图2中的相关参数进行整理得到反应动力学方程参数如表3 所示。将相关参数代入式（6）可计算出SiR材料的活化能为126.87 kJ/mol。

表3 反应动力学方程参数Tab.3 Parameters of reaction kinetics equation

计算得到Arrhenius 方程中的b=6 125，并结合表2，以1/T为横坐标，lnτ为纵坐标，得到5种断裂伸长保留率下，电缆附件用硅橡胶在不同温度的寿命曲线如图4所示。

图4 不同断裂伸长保留率下SiR寿命随温度的变化曲线Fig.4 Change curves of SiR life with temperature at different breaking elongation retention rate

GB/T 11026.2—2012[20]中建议将绝缘材料断裂伸长保留率为50%时作为绝缘材料热老化寿命的终点，取图4中断裂伸长保留率为50%的寿命曲线，得到SiR 材料分别在60、70、80℃下的预估寿命，分别为389 994 h（约44.5 年）、113 760 h（约13.0 年）、35 563 h（约4.1年）。

电缆长期带载时缆芯温度可达90℃，而附件界面温度常为60～70℃[21]，由此可知，若仅考虑硅橡胶材料的热学老化，工况下运行的电缆附件寿命应为13.0～44.5年。

然而实际上，由于极端天气环境[22]、附件受潮[23]以及人为破坏等诸多原因，加之早期附件安装工艺不佳导致界面存在集中性缺陷[24]，部分现场电缆附件的寿命往往远低于上述寿命预测值，而且本研究是采用50%断裂伸长保留率作为寿命终点，断裂伸长保留率为50%仅仅是从SiR材料特性本身出发的结果，考虑到电缆附件对保持电气性能所需要的界面压力要求，当断裂伸长保留率仅为50%时，界面压力已经远远不能保证电缆的电气性能。

因此，在后续电缆附件的发展中，对材料的改进与及时的寿命评估应当是重点发展的方向。