一种基于SPWVD-WVD的高质量时频分析方法及ISAR成像应用*

赵 婷,张成祥

(1.中国人民解放军陆军工程大学通信士官学校,重庆 400055;2.北京理工大学 重庆创新中心,重庆 401120)

0 引 言

时频分析方法是一种联合时间和频率的信号处理方法,它能够对非平稳信号进行直观处理和分析,是现代信号处理领域关键技术之一[1]。常用的时频分析方法分为线性时频分析方法和非线性时频分析方法。线性时频分析方法有短时傅里叶变换(Short-time Fourier Transform,STFT)[2]、小波变换[3]等。该类方法主要利用窗函数得到局部平稳信号,并且对多信号进行时频分析时不会产生交叉项,但该类方法的时频聚集性较差。而非线性时频分析方法具有良好的时频聚集特性,然而当对多信号进行时频分析时存在交叉项干扰。因此,在实际运用中容易产生虚假频率,导致最终分析结果较差。最典型的非线性时频分析方法为Wigner-Ville分布(Wigner-Ville Distribution,WVD)[4-5]。

为了获得良好的时频聚集性,同时避免交叉项干扰,国内外学者提出了多种时频分析方法,其中运用最广泛的是Cohen类时频分布方法,即利用不同的核函数与WVD进行二维卷积,从而抑制交叉项。如平滑Wigner-Ville分布(Smoothed Wigner-Ville Distribution,SWVD)利用高斯核对WVD进行平滑处理,从而减小交叉项的产生;伪Wigner-Ville分布(Pseudo Wigner-Ville Distribution,PWVD)通过加窗函数完成WVD在频域上的平滑,用于抑制WVD产生的交叉项[6]。然而上述算法在减少交叉项干扰的同时,也在一定程度上影响了WVD的重要性质,导致时频分布的分辨率较低。而SPWVD主要是利用两个窗函数分别对WVD的时域和频域进行平滑处理,虽然能够极大地抑制交叉项,但降低了一定的时频聚集特性,尤其是当信号带宽越宽时其时频分布的分辨率越差[7]。

针对上述问题,本文利用SPWVD与WVD之间的滤波互消效应,提出了基于SPWVD-WVD的高质量时频分析方法。该方法能够抑制交叉项的产生,同时也能够保留较好的时频聚集特性,实现信号时频分布特征的准确反映。通过仿真实验分析可知,本文提出的算法能够获得较好的时频分析结果。将本文算法成功应用于逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像系统中,获得了分辨率较高的成像结果。

1 基于SPWVD-WVD的时频分析方法

1.1 WVD原理

WVD是一种基本的二阶时频分布方法,具有良好的时频凝聚性。当信号为单分量线性调频信号时其时频聚集性较好,然而当信号为多分量线性调频信号时其时频分析结果受交叉项影响较为严重;并且对于高阶多项式相位信号,WVD还会产生自交叉项。假设解析信号为z(t),则其WVD的数学表达式为

(1)

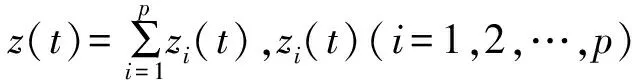
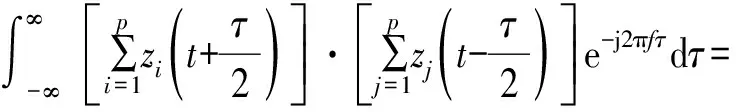
(2)

式(2)中第一项为信号自身项,第二项为交叉项。对于多分量信号,任意两个信号就会产生一个交叉项,且该交叉项位于两个信号频率分量的中间。交叉项将对信号本身项的理解产生极大的影响,尤其是在ISAR系统中,WVD中的交叉项会以虚假散射点的形式反映到ISAR成像当中,严重降低了成像质量。因此,需要进一步研究抑制WVD交叉项的方法[8]。

1.2 SPWVD原理

SPWVD是WVD的一种改进算法,它通过在时域和频域上分别调节两个窗函数来获得最优的时频分布,其数学表达式为

(3)

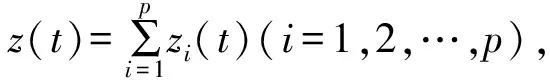
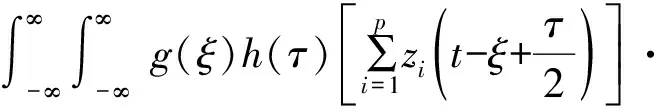
(4)

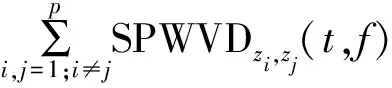
1.3 基于SPWVD-WVD的时频分析方法

为了抑制交叉项的同时保留高时频聚集性,本文提出了基于SPWVD-WVD的时频分析方法。算法具体实现思路如下:

1) 对输入信号进行WVD变换,得到WVDz(t,f)矩阵,如式(2)所示。

2) 对输入信号进行SPWVD变换,得到SPWVDz(t,f)矩阵,如式(4)所示;然后将SPWVD结果进行二值化处理,即

GSPWVD(t,f)=

(5)

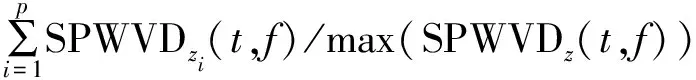
3) 利用WVD变换和SPWVD变换之间的滤波互消效应,抑制产生的交叉项的同时提高时频分析图的分辨率,即将WVD变换结果与SPWVD变换二值化结果进行矩阵运算,其数学表达式为

SPWVD-WVD(t,f)=GSPWVD(t,f)·WVDz(t,f)。

(6)

4) 输出SPWVD-WVD矩阵,得到最后的时频分析结果。

算法流程如图1所示。

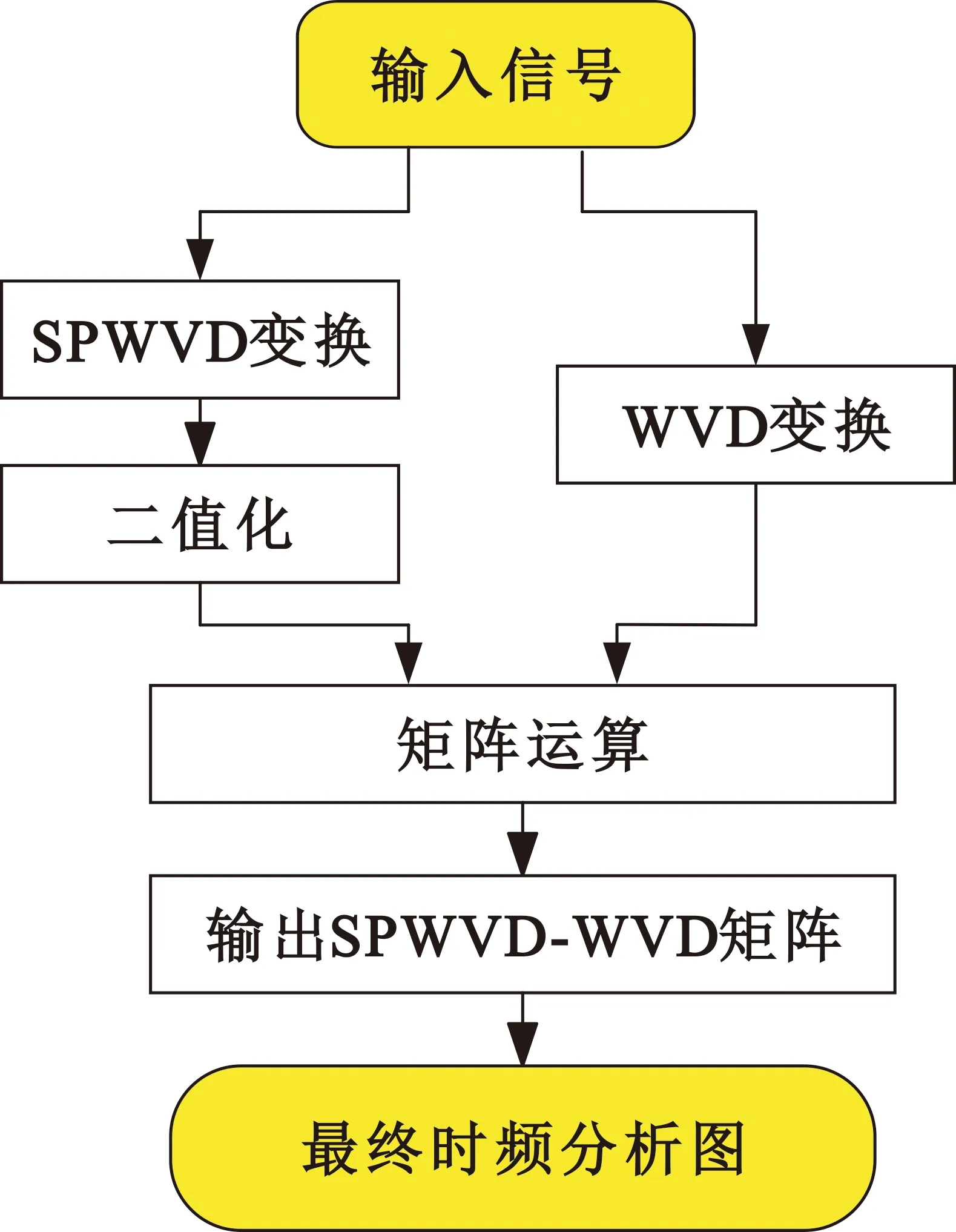
图1 SPWVD-WVD的时频分析算法流程

2 数值实验分析

2.1 仿真实验

为了验证上述算法的有效性,本文构造多分量线性调频(Linear Frequency Modulation,LFM)调频信号对提出的算法进行仿真分析,并与WVD算法、SPWVD算法进行分析比较。设输入信号为多分量LFM信号,其数学表达式为

(7)

式中:Ai为幅度值;ai0为中心频率,ai1为调频率值,i=1,2,3。相对应的仿真参数为A1=A2=A3=1;a10=80,a11=30,a20=150,a21=50,a30=-150,a31=-30;采样点数为256。图2为WVD算法、SPWVD算法以及本文提出算法的时频分析图,其中输入信号时频图如图2(a)所示,图2(b)为WVD算法的时频分析图。由图可知,WVD算法的时频聚集性较好,然而信号与信号之间产生了交叉项,严重影响了后续信号的分析处理。图2(c)为SPWVD算法的时频分析图,可见与WVD算法相比,SPWVD算法极大地抑制了交叉项的产生,然而却降低了时频分析的分辨率。图2(d)为本文提出算法的时频分析图,可见其不仅能够得到高分辨率的时频分析图,并且还抑制了交叉项的产生。因此,综上所述,本文提出的算法能够取得较好的时频分析结果。

2.2 算法性能评价

为了定量的分析提出算法的性能,本文从交叉项抑制和时频聚集度两方面来评价本文算法的有效性。

2.2.1 交叉项抑制评价

本文利用无交叉项信号的时变功率谱与各算法在时频平面上的时变功率谱之差作为交叉项抑制评价的标准,其中无交叉项信号的时变功率谱Ps为各分量信号WVD变换后的时变功率谱之和,其数学表达式为

(8)

式中:PWVD(k)为第k个信号分量WVD变换后的时变功率谱,k=1,2,3,…,N。交叉项抑制误差为[9]

(9)

式中:N为采样点数;P(i)为时变功率谱。

多分量LFM仿真信号s(t)的不同算法的交叉项抑制误差如表1所示。由表可知,WVD算法的交叉项误差最大,即WVD算法的时频分布产生交叉项较多,而经过SPWVD变换后,虽能够在一定程度上抑制交叉项,但交叉项抑制误差仍然较大,而本文提出的算法交叉项抑制误差最小,即能够很好地抑制交叉项误差。

表1 不同算法的交叉项抑制误差

2.2.2 时频聚集度评价

本文采用文献[10]中提出的时频聚集度评价方法来定量的分析仿真信号的时频聚集度,其表达式为

(10)

式中:Q为输入信号的时频分布;n为信号的时间窗宽度;ω为信号的瞬时频率值。则对于仿真信号s(t),其时频聚集度评价如图3所示,可知SPWVD算法的时频聚集度最差,在抑制交叉项的同时降低了时频聚集度。WVD算法的时频聚集度较好,但其交叉项误差较高,不利于后续的信号处理。而本文提出的算法的时频聚集度明显好于WVD算法,且能够很好地去除交叉项误差。因此,本文提出的算法能够得到高质量的时频分布图,较为准确地反映信号时频分布特征。

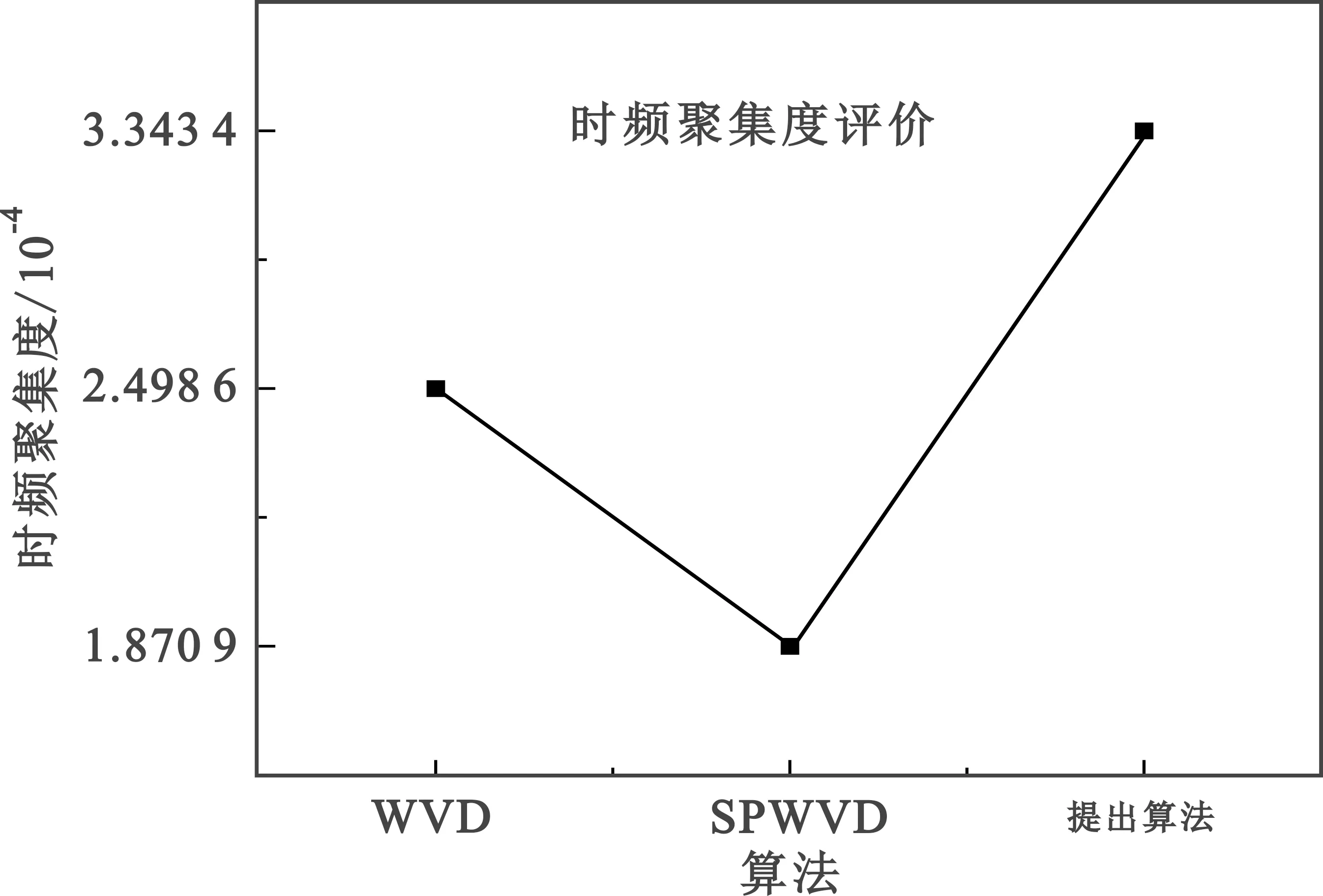
图3 WVD、SPWVD以及本文提出算法的时频聚集度值

3 ISAR成像应用

3.1 基于SPWVD-WVD的ISAR成像方法

ISAR是一种高分辨成像雷达,广泛应用于国土防御、空间探测等领域[11]。最常用的ISAR成像方法为距离-多普勒(Range Doppler,RD)算法[12]。该算法首先对ISAR回波信号进行距离压缩得到距离向高分辨率图像,然后对每一个距离单元数据进行频谱分析获得方位向高分辨,其中最基本的频谱分析方法为离散傅里叶变换(Discrete Fourier Transform,DFT)[13]。然而对于复杂的运动目标,其多普勒频率随着时间的变化而变化,运用RD算法会导致最后的成像结果产生散焦和拖尾。因此,传统的处理方法很难获得高质量的ISAR图像,需要采用时频分析方法对ISAR回波数据进行时频分析。该类方法不仅能够消除散焦和拖尾的影响,还能得到机动目标的瞬时多普勒频率分布图[14]。

在实际运用中,最典型的时频分析方法有WVD、SPWVD等方法。然而经过前面分析可知,WVD算法与SPWVD算法都不能够在抑制交叉项的同时获得较好的时频聚集特性。因此,本文利用SPWVD-WVD对回波信号进行成像,其成像处理流程如图4所示。即首先将ISAR回波数据进行距离压缩处理获得距离向高分辨率图像,然后运用SPWVD-WVD算法对每个距离单元的回波数据进行时频分析,最后通过时间采样得到运动目标的瞬时多普勒频率ISAR图像。

图4 基于SPWVD-WVD算法ISAR成像流程

为了验证上述算法的性能,本文利用仿真数据进行分析验证,假设、信号的采样频率、载波频率、传输带宽、脉冲重复频率分别为200 MHz,9.8 GHz,150 MHz,200 Hz。图5为不同算法的ISAR仿真结果图。

图5(a)为RD算法成像结果,出现了散焦和拖尾的现象。图5(b)为WVD算法成像结果,其成像模糊不清。图5(c)为SPWVD算法成像结果,其成像出现了散焦。经过距离压缩后得到了距离向高分辨率图像,图5(d)为最终的ISAR成像结果,可见经过SPWVD-WVD算法时频分析后能够消除散焦和拖尾等影响,得到高质量的ISAR成像结果图。

3.2 全局阈值Ta的选取

本文采用最大类间方差(Otsu)法计算全局阈值Ta[15],即将成像结果分为目标和背景两类,利用类间距离极大准则来确定最佳阈值,其计算公式为

Ta=P1(m1-m0)+P2(m2-m0)。

(11)

式中:P1和P2分别为目标和背景出现的概率;m1和m2分别为目标和背景的灰度均值;m0为成像结果的灰度均值。

图6～8为不同Ta时不同信噪比(Signal-to-Noise Ratio,SNR)的ISAR成像结果,其中图7为最佳阈值。由图可知,当Ta值小于最佳阈值时,最终的成像结果易受到SNR的影响,尤其当SNR越低时最终的成像结果越不理想,如图6所示;当Ta值大于最佳阈值时,受到SNR的影响较小,但容易导致目标重要信息的缺失,如图8所示。因此,本文采用Otsu法来确定最佳阈值,从而获取最佳的成像结果。

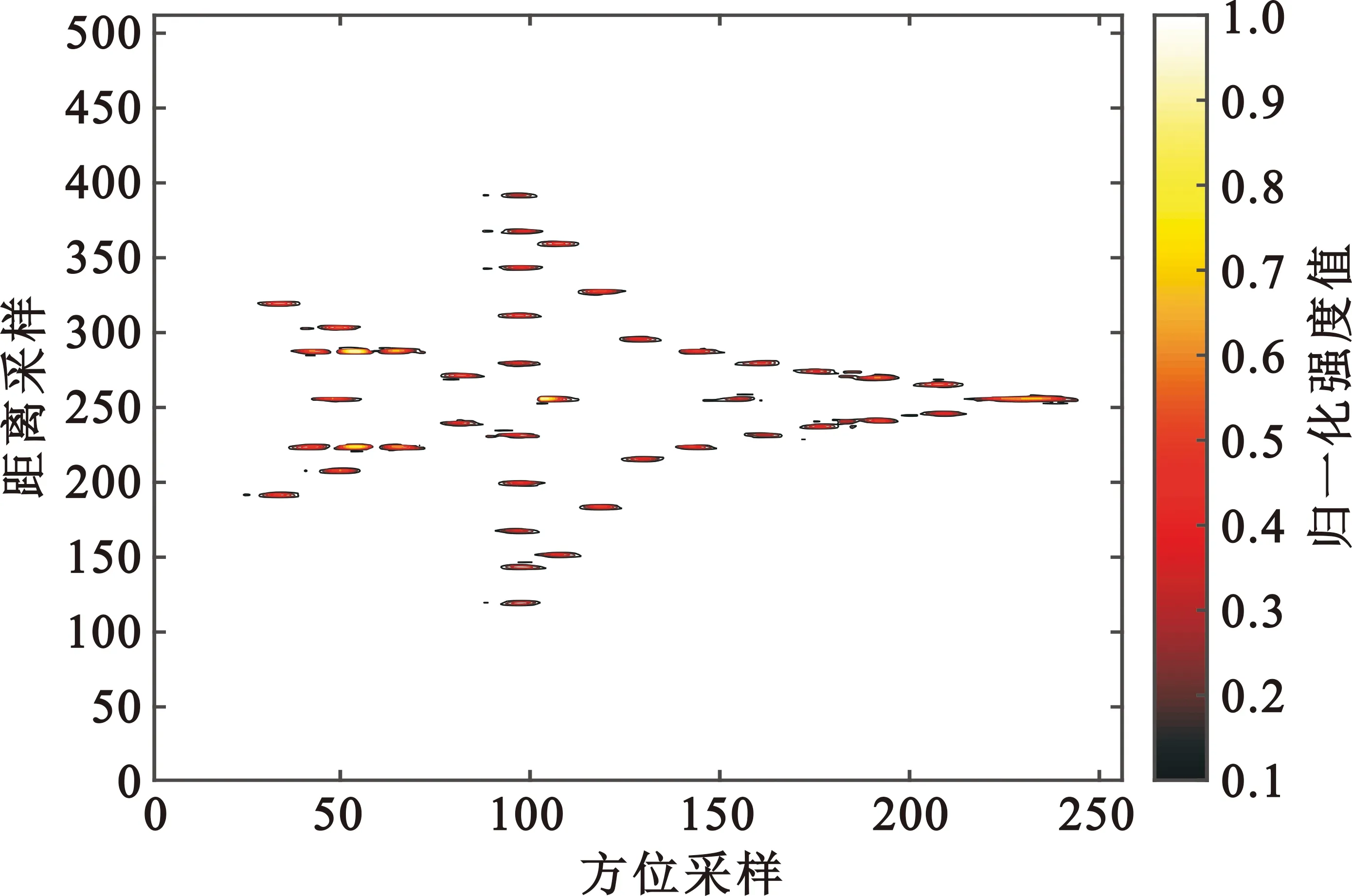
(a)SNR=0 dB

(a)SNR=0 dB

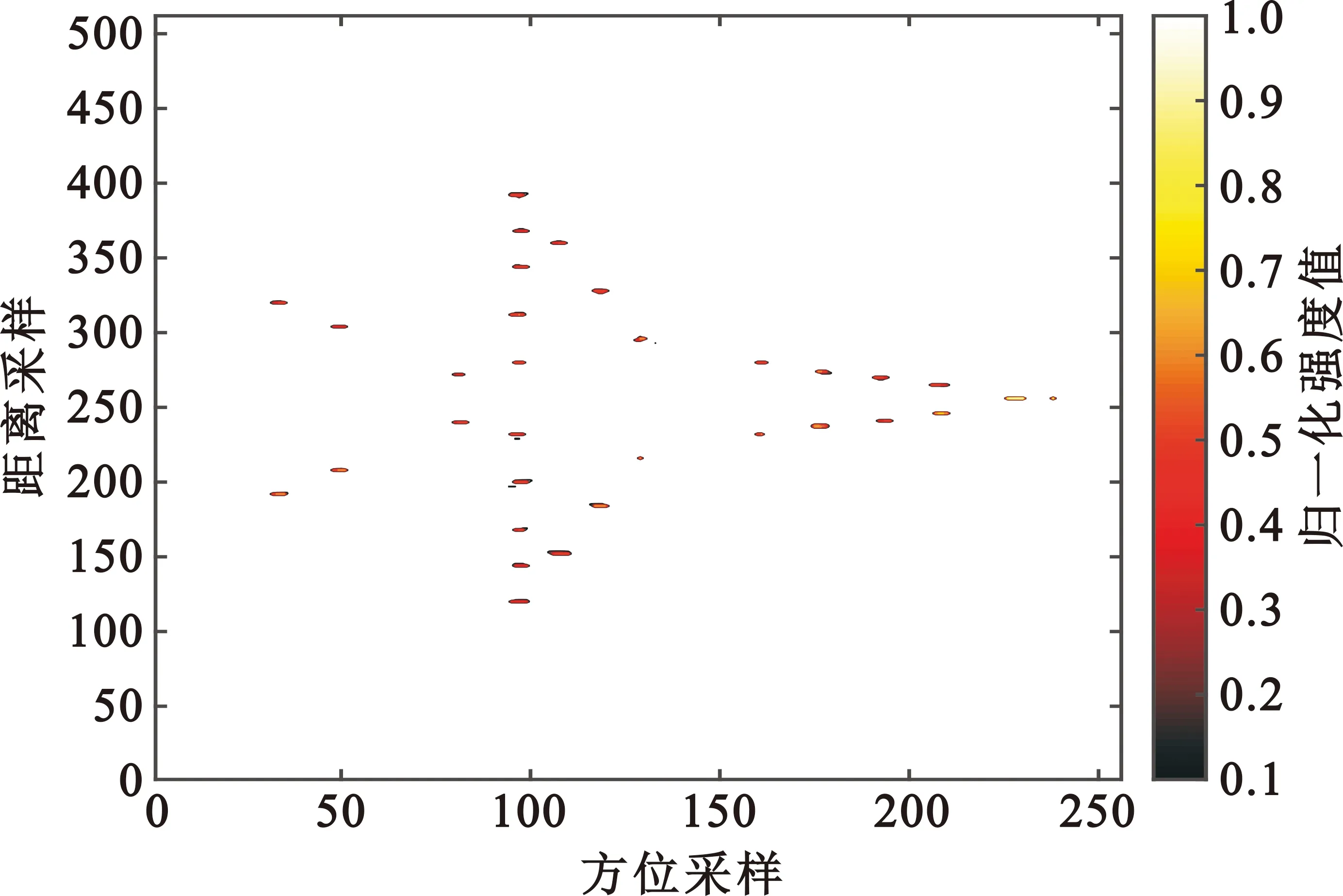
(a)SNR=0 dB

3.3 实测数据分析

为了更进一步验证改进后的时频分析算法的成像效果,本文选用C频段、带宽400 MHz的波音B727飞机的实测数据信号对RD算法、WVD算法、SPWVD算法以及本文提出的算法进行对比分析,脉冲宽度为25.6 μs,脉冲重复频率为100 Hz,ISAR成像结果如图9所示。图9(a)为RD算法的成像结果,可见得到的目标图像有严重的散焦和拖尾现象,严重影响后续的信号处理。图9(b)为WVD算法成像结果,可见受交叉项的影响导致最后的成像结果模糊不清。而SPWVD算法虽然抑制了交叉项的影响,但在一定程度上减小了时频聚集度,导致最后成像结果不理想,如图9(c)所示。图9(d)为本文提出算法的成像结果,可见其较为清晰。与上述算法相比,本文提出的算法不仅消除了交叉项的影响,还提高了时频聚集度。

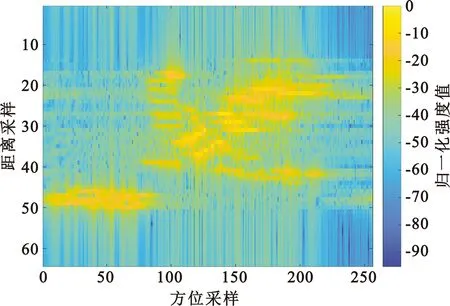
(a)RD算法成像结果

本文采用信息熵来分析ISAR目标图像的成像质量,其数学表达式为

lb abs(s(i,j)2)+lb(E)。

(12)

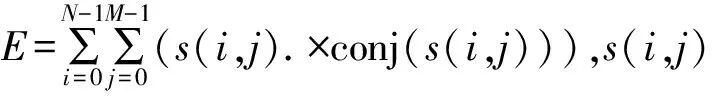
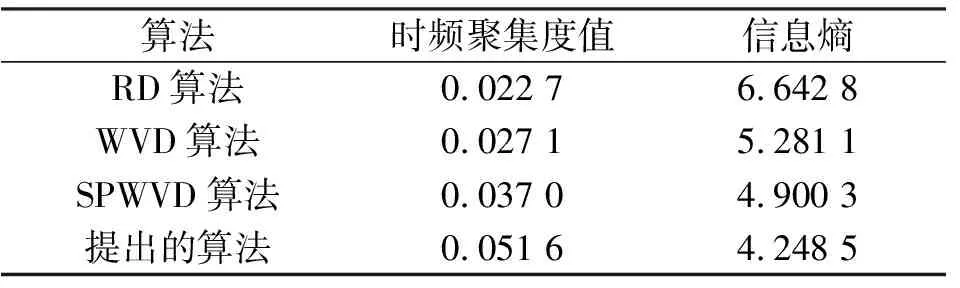
表2 不同算法的时频聚集度值及信息熵值

3.4 运算复杂度分析

设距离向采样点数为Nr,方位向采样点数为Na,则RD算法的运算复杂度为

CRD=O(2Nr×Na×lb(Nr)+2Nr×Na×lb(Na))。

(13)

基于SPWVD的ISAR成像算法总的计算复杂度主要有距离校正和时频分析,其表达式为

CSPWVD=O(Nr×Na×lb(Nr)+Nr×Na×lb(Na)+Nr×Na)。

(14)

根据图4所示的基于SPWVD-WVD的ISAR成像算法实现流程图,本算法总共进行了Nr次Na维FFT,一次SPWVD运算和WVD运算,以及一次二值运算和矩阵运算,其运算复杂度为

CSPWVD_WVD=O(Nr×Na×lb(Nr)+

Nr×Na×lb(Na)+

2Nr×Na+2Nr×Nr)。

(15)

根据上述分析可知,SPWVD算法的运算复杂度最低但都不能同时抑制交叉项和获得高的时频聚集特性;RD算法不仅运算复杂度更高,而且得到的最后的成像结果产生了严重的散焦和拖尾。因此,与上述两种方法相比,本文算法的性能更好,在工程实现中具有一定的优势。

4 结 论

本文分析了WVD与SPWVD两种算法原理,针对交叉项干扰和时频聚集度问题提出了SPWVD-WVD的时频分析算法。该算法利用WVD与SPWVD的滤波互消效应,不仅抑制了交叉项还提高了时频聚集度。数值仿真结果表明,本文提出的算法能够获得高质量的时频分布图。将本文算法用于ISAR成像,能够得到高分辨率的ISAR目标图像,为后续信号处理提供了有效依据。