脆性各向同性材料的强度准则数学形式研究
2023-10-30汪璋淳张桂荣梅聚福刘中仪
孔 洋,汪璋淳,张桂荣,张 贤,梅聚福,刘中仪
(南京水利科学研究院岩土工程研究所,江苏 南京 210024)
0 引 言
在岩石强度准则研究中,线性摩尔-库伦(M-C)准则适用于较低应力水平情形,较高围压工况下其描述的岩石强度随围压线性增大的特征与实际岩石力学试验结果不符[1];胡克-布朗(H-B)准则能反映岩石强度随围压非线性增长的特征,但存在一定程度的高应力条件下过高估计岩石强度的问题[2-3]。除经典M-C准则与H-B准则外,常用的岩石强度准则还有指数型强度准则[4]与幂函数形式强度准则(如Bieniawski准则[5]、Balmer准则[6-7]等),各强度准则数学表达形式不一,其适用性应根据岩石类型、节理裂隙发育情况、围压工况以及是否考虑抗拉强度指标等具体分析。
国内外学者基于岩石临界状态或岩石临界围压概念,对经典M-C准则与H-B准则进行了改进研究[8-9],认为岩石进入临界状态后其剪切应力及对应的偏应力不再随围压发生变化,岩石进入临界状态所对应的围压即临界围压[1]。针对不同类型的岩石,虽然临界状态围压取值差异性较大,但既有研究成果均依据围压增大到一定量值时偏应力趋近于常数概念进行状态判定。
笔者采用1stOpt软件并基于共轭梯度法CGM+全局优化算法研究发现,修正M-C准则[10]与修正H-B准则[11]在数据拟合过程中参数极易出现负数项,表明利用临界围压状态概念改进后的强度准则参数稳定性较低,在脆性类岩石材料方面的适用性存在一定不足之处。为此,本文针对一种用于研究完整玄武岩块体力学行为的典型脆性各向同性材料[12-14],探究了H-B准则、Power Curve准则与单参数Bieniawski准则等3类岩石经典非线性强度准则与Singh抛物线型强度准则的适用性,基于临界围压概念引入参数n,对Singh抛物线型强度准则数学形式进行了修正。
1 脆性类岩石水泥砂浆材料
制备一种脆性各向同性质量比为水泥∶河砂∶水∶减水剂=1∶0.5∶0.4∶0.002的试样[12-14],试样制备与试验方案参照GB/T 50266—2013《工程岩体试验方法标准》,采用MTS311.31S型电液伺服试验机开展单轴压缩与巴西劈裂试验,采用Hoek三轴试验装置开展不同围压工况下的三轴压缩试验。试验预设9组围压工况,分别为0、1.5、3.0、4.5、6.0、6.4、7.5、10.5 MPa和14.0 MPa。实测水泥砂浆材料的平均单轴抗压强度为70.40 MPa,平均抗拉强度为4.43 MPa,基于前3组围压工况计算得到内摩擦角为31.26°,材料压拉比为15.89。
基于脆性类岩石水泥砂浆材料三轴试验结果,可将强度指标整理成如图1所示的3级围压段摩尔圆及其切线簇。图1中,围压段1为0~3.0 MPa,围压段2为4.5~6.4 MPa,围压段3为7.5~14.0MPa。相似模型材料平均单轴抗压强度为70.4 MPa,其中3.0~4.5 MPa围压区间内包含5%峰值抗压强度点3.52 MPa,6.4~7.5 MPa围压区间内包含10%峰值抗压强度点7.04 MPa。从图1可以看出,不同围压段内近似线性的强度包络线差异较大,表明脆性类岩石水泥砂浆材料不同围压下,强度包络线切点斜率是连续变化的曲线,即表现出典型强度演化非线性特征。

图1 摩尔圆及其切线簇
2 经典岩石强度准则适用性研究
根据国内外研究成果,选取H-B准则、Power Curve准则与单参数Bieniawski准则等3类经典岩石强度准则,探究其对脆性类岩石水泥砂浆材料的适用性,利用非线性最小二乘优化方法确定强度准则参数,以拟合值与试验值的残差平方和RSS[15]最小作为定量评价依据,强度准则参数通过RocData软件计算或1stOpt软件非线性回归分析得到。
为克服H-B准则在工程应用中的不足与局限性,Hoek与Brown多次对强度准则进行了补充与修正,得到广义H-B准则的表达式,即
σ1=σ3+σc(mbσ3/σc+s)κ
(1)
式中,σ1为最大主应力;σ3为最小主应力;σc为岩石类材料单轴抗压强度;mb为描述岩体强度特征的折减材料参数;s为经验参数,对于完整岩石材料取1;κ为材料常数。
大量试验结果表明黏土、堆石料与节理岩体等岩土材料失效包络线是非线性的,特别是在较低法向应力应力状态下,非线性特征比较显著,该类型强度包络线对应的剪应力τ与法向应力σn的关系符合Power Curve模型形式,即
τ=a(σn+d)b
(2)
式中,a、b与d为试验参数。
1974年Bieniawski提出了幂函数形式强度准则,用以评估岩石的强度参数,即
(3)
式中,e为试验参数。
3类经典非线性岩石强度准则对9组围压工况试验数据拟合结果见图2。从图2可知,3类强度准则拟合结果中,单参数Bienianski准则RSS值仅为0.019,为最优拟合模型,可较好反映脆性类岩石材料非线性强度特征,但单参数Bienianski准则无拉应力象限,故无法考虑抗拉强度对强度指标的影响;H-B准则与Power Curve准则均能反映抗压强度指标的非线性特征,但两者均过高估计了抗拉强度值,即基于H-B准则的抗拉强度拟合值为9.39 MPa,基于Power Curve准则的抗拉强度拟合值为6.09 MPa,实测值为4.43 MPa。
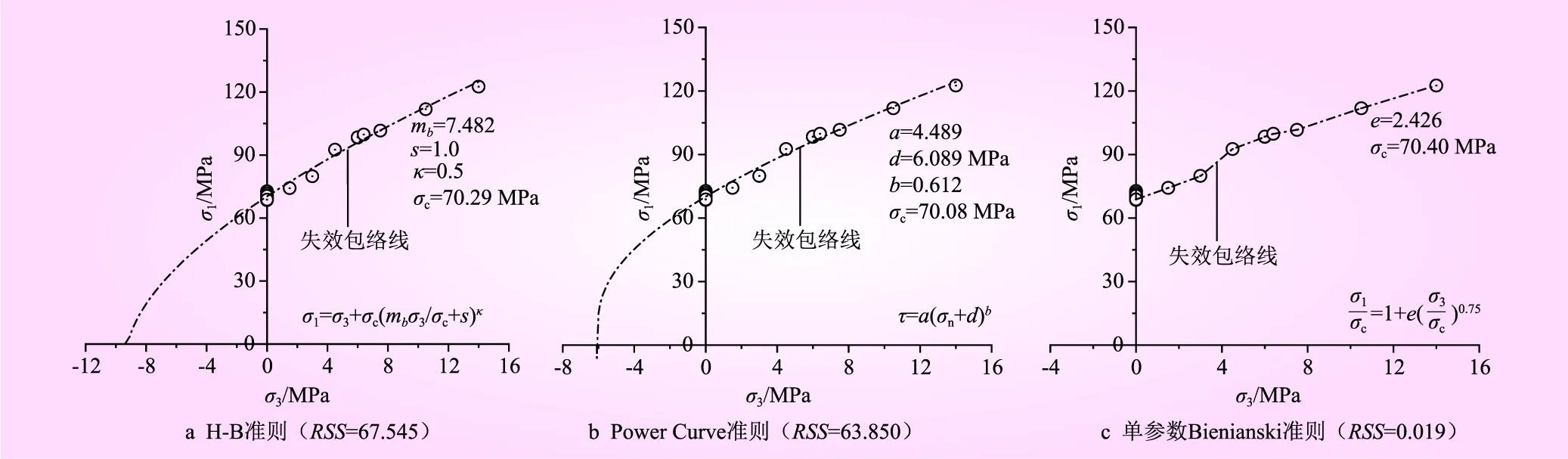
图2 经典非线性岩石强度准则试验数据拟合结果
3 Singh抛物线型强度准则修正研究
3.1 Singh抛物线型强度准则基本形式
对于各向同性的干燥岩石材料,M. Singh与B. Singh于2005年提出了一种形式简单、非线性的抛物线型强度准则[16],即
(4)
式中,(σ1-σ3)为偏应力;A0、B0与C0为试验参数,可由下述边界条件计算得到,即
假定当σ3=σc时岩石进入临界状态,即临界状态围压值σcrt=σc,则Singh抛物线型强度准则的具体形式可表示为
式中,B0=-2A0σc,C0=σc,此时σc为试验已知值,仅有的未知项A0可由下式推算
(7)
3.2 Singh抛物线型强度准则适用性研究
本文选用的脆性类岩石水泥砂浆材料属于标准的各向同性材料,同时在试样制备阶段进行了充分干燥,故基于Hoek三轴试验结果式(4)中C0项应取为试验值70.40 MPa,A0项由式(7)计算,为-0.106,则B0项应为14.883,则依据本文试验结果,式(4)应表述为
(8)
Singh抛物线型强度准则试验数据拟合结果见图3。从图3可知,式(8)所述曲线与试验值偏差明显,B0=-2A0σc项是导致曲线数值偏大的主要原因,故M. Singh与B. Singh给出的抛物线型强度准则假定岩石材料进入临界状态的围压σ3=σc的设想是值得商榷的,应对强度准则进行修正。

图3 Singh抛物线型强度准则试验数据拟合结果
3.3 Singh抛物线型强度准则的修正形式
式(4)在数据处理时,可等效为因变量(σ1-σ3)与自变量σ3的二次多项式数据拟合,笔者得到脆性类岩石水泥砂浆材料的修正Singh抛物线型强度准则试验数据拟合结果见图4。图4中,σ3i为试验材料进入临界状态的围压值;σcrti为临界状态围压计算值。从图4可以看出:
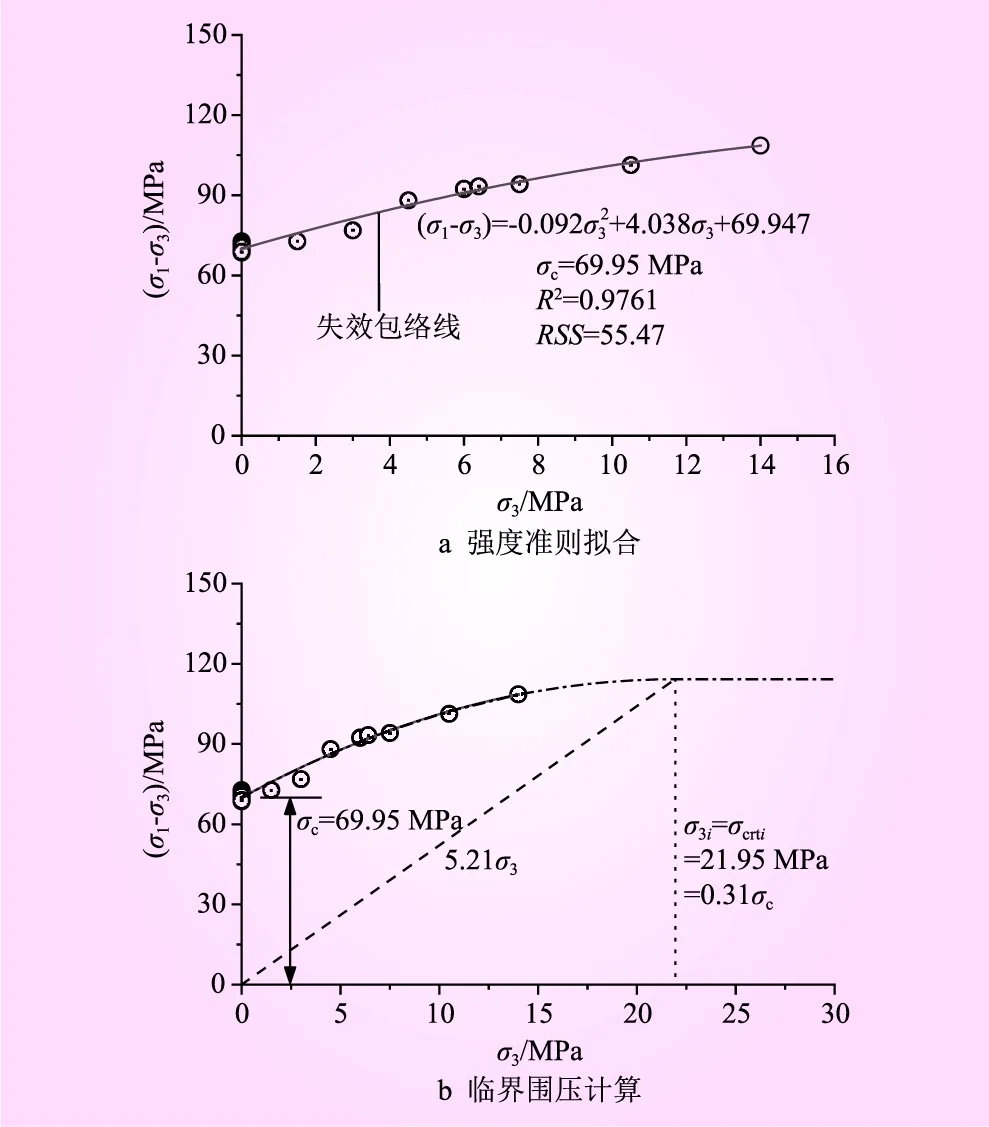
图4 修正Singh抛物线型强度准则试验数据拟合结果
(1)式(4)中,C0项本应取为试验值70.40 MPa,但二次多项式拟合预估值约为69.95 MPa,与试验值相对误差绝对值仅为0.64%,偏差较小,故将Singh抛物线型强度准则等效为二次多项式拟合,并取拟合值C0项进行研究是合理的。
(2)将Singh抛物线型强度准则数学形式等效为因变量(σ1-σ3)与自变量σ3的二次多项式,数据拟合相关系数R2=0.976 1、残差平方和RSS=55.47,拟合效果较好;仅在1.5 MPa与3.0 MPa低围压数据点存在一定偏差。

M. Singh与B. Singh给出的抛物线型强度准则假定岩石材料进入临界状态的围压σ3=σc,实际临界围压值远比σc值小;可引入参数n表征岩石进入临界状态时围压σcrt=nσc,对Singh抛物线型强度准则数学形式进行了改进,将式(5)修正为
将式(4)代入式(9),可得修正的Singh抛物线型强度准则具体数学表达式为
式中,B0=-2A0nσc,C0=σc,此时σc可取试验已知值或强度准则公式数据拟合值,A0与n可由试验数据进行二次多项式拟合得到。
4 结 语
本文针对可模拟完整玄武岩块体力学行为的脆性各向同性材料,探究了胡克-布朗(H-B)准则、Power Curve准则与单参数Bieniawski准则等3类岩石经典非线性强度准则与Singh抛物线型强度准则的适用性,并对Singh抛物线型强度准则数学形式进行了修正,得到以下结论:
(1)单参数Bienianski准则可较好反映脆性类岩石水泥砂浆材料非线性强度特征,数学形式拟合值与试验值的残差平方和(RSS)最小,但Bienianski准则无拉应力象限;H-B准则与Power Curve准则均能反映抗压强度指标的非线性特征,但两者均过高估计抗拉强度值。
(2)将Singh抛物线型强度准则数学形式等效为因变量(σ1-σ3)与自变量σ3的二次多项式,数据拟合效果较好,得到脆性类岩石水泥砂浆材料进入临界状态的围压σcrt=0.314σc。
(3)M. Singh与B. Singh给出的抛物线型强度准则假定岩石材料进入临界状态的围压σ3=σc,实际临界围压值远比σc值小;通过引入参数n表征岩石进入临界状态时围压σcrt=nσc,得到了改进的Singh抛物线型强度准则数学形式。
