基于p-y 曲线法的深埋桩桩-土相互作用研究
2023-10-30张培强黄桂祥林荣顺
司 翔, 张培强, 黄桂祥, 林荣顺
(中国建筑第七工程局有限公司, 河南 郑州450000)
0 引言
桩基础常用于软土地区的地基处理之中, 在软土地基中埋入桩基可以提升地基承载力, 防止下沉。 近年来, 随着经济建设的快速发展和施工技术的不断进步, 在全国各地新建了许多的超高层建筑, 对基础中单桩承载力的要求也在不断提高。 桩基础特别是超长桩, 因其具有较高的单桩承载力而被广泛的应用于各类建筑之中。 然而,目前有关超长桩的理论计算方法相对滞后, 在实际工程中通常采用普通桩柱的计算方法对超长桩进行计算。 但在实际工程中, 超长桩和普通桩之间工作原理、 变形特征存在一定的差异, 时常出现理论计算结果与实际情况不相符的现象。 因此,针对超长桩的理论计算模型的研究不仅有助于桩基础理论研究的发展, 也有助于解决工程建设领域的一些难题。
对于超长桩的界定, 在学术界目前还没有一个统一的判断方法, 不同领域关于超长桩的划分界限有所不同。 通常认为当桩的总长L≥50 m 且桩的总长L 与桩的直径D 的比值L/D≥40 时可作为超长桩进行分析[1]。 由于工程建设的需要, 许多专家学者针对具体的工程结构提出了对应的超长桩的理论计算模型。 李韬[2]通过群桩试验分析得到适用于软土地区桩基沉降量的估算方法; 蒋建平等[3]通过现场试验比较了大直径超长桩桩身总侧阻力与端阻力的承载特性; 李传勋等[4]在综合考虑桩侧土抗力、 桩侧摩阻力以及自重的影响之后, 总结出了可用于计算超长桩屈服荷载和有效长度的计算方法; 郑刚等[5-6]通过有限元分析计算了超长桩的荷载传递特性; 姚文娟等[7]利用侧位移修正法计算了分层土中受水平荷载的超长桩的侧位移解; 林骁骋等[8]采用有限元法分析了边载和水平荷载共同作用下的超长桩的承载性状;谢新宇等[9]在考虑桩土相对位移的基础上, 通过Geddes 应力法计算了成层土中桩基的沉降量; 杨明辉等[10]通过理论推导出了桩侧摩阻力在桩周围土体产生的位移场, 得到了可用于分析计算群桩相互作用时桩侧单位土体的计算方法。 此外, 还有部分学者对软土地基中长桩的极限承载力分析方法、 多层地基中超长桩荷载传递的非线性计算方法等进行了深入研究, 并得到了许多经典理论[11-13]。
以上研究主要集中于超长桩的轴向荷载传递理论、 群桩的侧摩阻力等方面, 然而在实际工程中, 超长桩受到的荷载是由多个因素产生的, 荷载的作用方式也是多样的, 这就导致了桩基础在实际工作中不仅要受到纵向荷载, 同时也有可能受到水平荷载或倾斜荷载在水平方向的分项的共同作用[14], 常导致模型计算结果与工程实际之间存在较大出入的问题。 因此, 本文基于上述研究,将轴向荷载产生的横向作用等效为横向荷载, 并根据弹性力学中的变分原理得出对称的有限元刚度矩阵, 与p-y曲线相结合, 建立起考虑土抗力分布的超长桩单桩内力位移求解的非线性有限元计算模型, 并以新玺中心-钻孔灌注桩工程为背景建模分析, 以验证本模型的正确性。
1 p-y 曲线模型的建立
当桩顶的水平荷载增加时, 在桩柱周围土体的塑性区将沿着桩柱向下扩张, 然后根据不同荷载作用下桩柱土体周围的最终位移来区分土体的弹性区域和塑性区域, 最后分析出地基反力的方法称为p-y曲线法。p-y曲线法是一种用来描述桩-土之间相互作用力p与桩身位移,y和桩的埋深深度之间的曲线关系, 因此p-y曲线法的关键就是确定p-y曲线。 目前, 国内外的专家学者通过试验的方法得出许多关于p-y曲线的确定方法,本文根据不同土体性质选取p-y曲线确定的方法如下。
1.1 不同土体p-y 曲线的确定
1.1.1 砂土
本文利用Atanh(B) 的双曲正切函数来描述砂土的p-y曲线, 该曲线的参数A、B比较容易求得。 砂土的p-y曲线公式为:
上述公式中的k(φ) 是砂土的初始模量, 与土体内摩擦角φ有关, 可根据公式(2) 拟合求得。
式中的极限抗力pu的计算方法如下:

1.1.2 黏土
对于黏土的p-y曲线, 本文根据试验结果和相关学者的研究结论[15-17], 确定出黏土的p-y曲线形式如下:

上述公式中的Cu为不排水时的抗剪强度;γ为土体的平均重度;z为计算土体抗力时桩的对应深度;D为桩的半径;J为经验系数, 本文取为0.5。
1.2 p-y 曲线非线性弹簧设置方法
本文在综合分析了前人的研究结论后, 提出采用Newmark 弹簧的设置方法和有限杆单元的等效荷载求解原理综合得出与p-y曲线相适应的非线性弹簧的设置方法。 基于上述设置方法, 将超长桩沿桩长方向划分为多个区段, 每段设置一个等效弹簧支座并设置弹性系数, 把超长桩的非线性求解问题转化为简支梁问题进行求解。 根据上述原理, 将桩的埋入深度设为h, 整个桩基共分为了n个区段, 则每个区段的长度L=h/n, 将桩上任意一点的弹性系数设为k(z), 则第i个弹簧的弹性系数可由下列公式进行设置:
可将上述公式用于求解有限杆单元中的水平抗力节点弹簧。 将水平抗力的影响范围假设为节点上下两个单元的一半, 公式(12) 中积分的上下限取对应节点的上下单元的1/2, 由于这种假设将杆中的实际抗力做了过多简化, 容易导致计算结果与实际情况之间存在较大出入, 因此, 需对上述方法进行改进。 假定在埋深深度为z的桩上的土体抗力p(z) 与水平位移y(z) 之间为线性关系, 则:
公式中的punit(z) 为单位位移下的水平抗力。将各单元产生aunit位移时所需要的等效应力记为, 可将公式(12) 改写为:
由p-y曲线法可知, 在埋深为z处的桩身受到的土体水平抗力为p(z,y(z) ), 采用迭代法取任意迭代步骤中水平位移y(z) 与土体水平抗力p(z,y(z) ) 的线性弹簧系数作为下一步迭代的基本弹簧系数:
在计算过程中,y(z) 为已知量, 故可将土体的水平抗力表示为:
对于纯弯杆单元的等效荷载, 可按下式计算:
公式中的zi,zi+1为第i,i+1 个桩节点在土体中的埋深深度,N为纯弯梁的插值函数矩阵[14],综合公式(16)、 (17), 可得:
公式中的ξ可按下式计算:
将公式(18) 进行非线性方程组迭代计算,在进行迭代计算时, 可将上一步计算所得位移向量通过公式(18) 求出等效水平土抗力的影响矩阵。 为使模型计算结果更贴合实际, 需要充分考虑多项因素的影响, 本文将轴向荷载的影响考虑进去, 将有限元求解方程改进为如下所示:

2 模型验证
2.1 工程背景介绍
拟建新玺中心项目, 该项目包括上部结构47 层建筑, 1 层至4 层为综合文化活动中心等, 5 层-44 层为商务办公, 标准层层高4.1 m; 45 层-47 层为综合文化活动中心、 大堂等, 层高为4.0 m~8.0 m; 11、 23、 35 层为安全层, 层高为4.9 m, 地下3层为车辆仓库和装备仓库, 人防区域则在地下室三层, 平战结合, 平时为车辆仓库。 负一层层高为6.0 m, 负二、 三层每层高度为3.9 m。 塔楼主要采用大直径冲孔灌注桩, 而裙楼和地下室则使用预应力管桩。
地貌单元属于河流冲积、 淤积平原地貌。 现有场地为空地, 场地由于建筑垃圾堆填, 地势略有起伏, 地面现有标高在7.31 m ~9.54 m 间。 根据土层的岩性, 将其基础土层划分为12 层, 其层厚、 类型、 深度等详细情况如表1 所示。 根据地基土的具体情况, 在成桩方法中, 选用了深埋式钻孔灌注桩, 其设计参数为: 在水下采用C50 级强度混凝土, 采用1.5 m 直径、 71 m 长的桩基。主要钢筋是26φ22 的通长钢筋, 其抗拉强度和抗弯强度均高于普通钢筋。 按规范规定设计计算的单桩承载力为Qu=23800 kN。
该工程的持力层为中等(微) 风化花岗岩层,整个桩端截面进入持力层的深度大小不低于0.5 m。
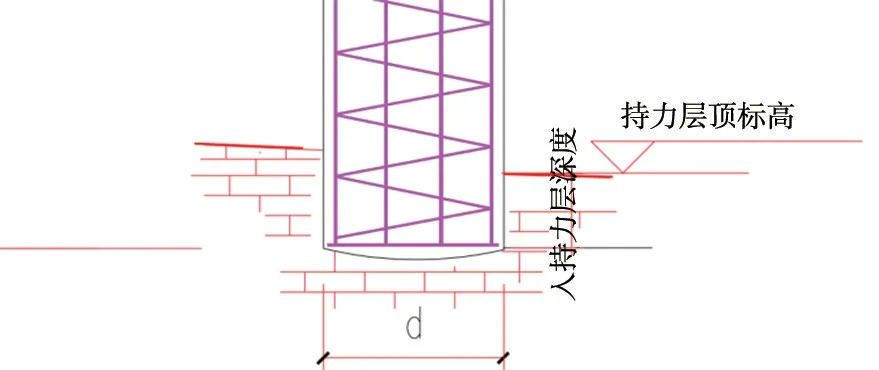
图1 灌注桩桩底进入持力层示意图Fig.1 Schematic diagram of cast-in-place pile bottom entering the bearing layer
2.2 数值模拟分析
以上述工程为建模对象, 利用ABAQUS 软件进行有限元分析。 建模过程中的网格划分如图2所示:

图2 网格划分Fig.2 Grid division
土体及桩基实体单元均采用C3D8 三维8 节点的网格划分技术, 边界条件设置为土体底部全约束, 桩基周围的土体侧向约束。 在桩顶施加上水平方向0.5 m 的位移荷载, 桩基内部应力变化如图3 所示。

图3 荷载作用下桩基础应力变化Fig.3 Stress change of pile foundation under load
由桩基础端部承受荷载后的内部应力变化可知, 在加载初期自桩基础顶端向下, 受到荷载影响, 桩基础周围土体的应力分布为“M” 型, 即越靠近桩基础的土体竖向应力越大, 且在桩基础周围土体出现多个“M” 的应力分布; 当加载进行到中后期时, 桩基础周围土体的“M” 型应力分布数量逐渐消失, 说明由于桩基础受水平荷载产生的土体应力随着土体的变形而逐渐消失, 即土体产生了位移。 加载过程中桩基础周围土体的土压力和桩侧水平位移如图4、 图5 所示。
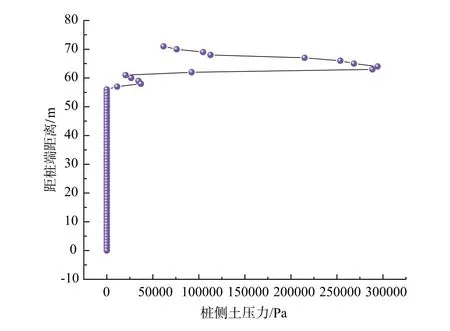
图4 桩侧土压力分布Fig.4 Distribution of soil pressure on pile side
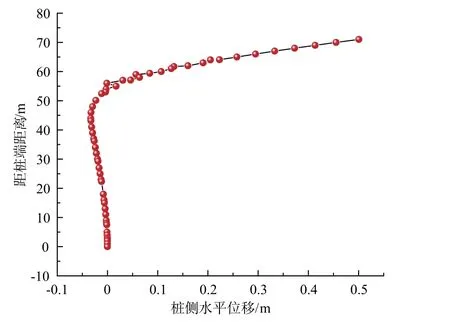
图5 桩侧水平位移Fig.5 Horizontal displacement at pile side
从图4 可以看出, 加载结束后, 当桩基础埋深深度为55 m, 桩侧土压力基本为0; 当埋深深度大于55 m, 桩侧土压力开始增加, 最大土压力达到了34 kPa。 桩侧水平位移如图5 所示, 从图中可以看出, 在埋深深度为7.5 m~57 m时, 桩侧发生的水平位移为负, 即桩侧产生的位移与水平加载的位移方向相反, 最大位移为3.3 mm, 埋深深度为44 m; 在埋深深度为57 m ~71 m时, 桩侧水平位移为正, 即桩侧水平位移方向与荷载方向一致,最大位移为550 mm, 在桩基础底端, 与桩顶所加的水平荷载大小相同。
为验证有限元分析的准确性, 选取部分与现场桩基观测点所对应的桩侧土压力和桩侧水平位移进行对比分析, 实测数据与模拟值及两组数据之间的相对误差分布如表2 所示。

表2 实测值与模拟值的结果比较Table 2 Comparison of measured and simulated values
由表2 可知, 通过数值模拟分析计算所得与现场实测数据之间的相对误差较小。 其中, 各实测点的桩侧土压力与模拟值之间的相对误差均小于2%; 实测的桩侧水平位移与模拟值之间的相对误差基本保持在5%以下, 仅埋深为10 m 处的实测值与模拟值之间的相对误差较大, 为17.6%,但观察此处桩侧的实际水平位移和数值模拟分析计算出来的水平位移可以发现, 实测值为-2.5 mm,模拟值为-2.94 mm, 两者之间仅相差0.44 mm, 在实际工程中可忽略不计。 由此说明通过ABAQUS 软件模拟桩基础受到水平荷载后产生的土压力和水平位移与实际情况基本一致, 可根据数值模拟结果对桩基础结构进行分析, 也说明可利用数值模拟结构来验证p-y曲线模型的准确性。
2.3 p-y 曲线模型验证
根据公式(1) ~公式(20) 的计算方法, 利用MATLAB 软件编制p-y曲线的计算程序, 计算得到桩侧土压力和桩侧水平位移。 由于现场试验条件有限, 不可能对桩基础各个部位进行实际测量, 故无法验证p-y曲线模型是否可准确计算出桩基础各个部位的实际情况; 但根据3.2 节中数值模拟结果和实测值之间的对比分析结果可知,数值模拟结果与实测值之间的差异不大。 因此,本文利用数值模拟结果验证p-y曲线模型的准确性。 由p-y曲线模型与数值模拟结果得到的桩侧土压力分布和桩侧水平位移分布分别如图6、 图7所示。

图6 桩侧土压力对比图Fig.6 Comparison diagram of soil pressure at pile side

图7 桩侧水平位移对比图Fig.7 Comparison diagram of horizontal displacement at pile side
综合图6、 图7 可知, 本文提出的p-y曲线模型计算得到的桩侧土压力和水平位移与数值模拟结果基本相同, 数值模拟结果均分布于模型曲线两侧。 相关性分析发现, 根据p-y曲线模型计算得到的桩侧土压力曲线与数值模拟计算结果之间的相关系数R2为0.97, 模型计算得到的桩侧水平位移曲线与数值模拟结果之间的相关系数R2为0.92。 由此说明本文提出的p-y曲线模型可用于分析超长桩承受水平荷载时的桩侧土压力和桩侧水平位移。 在运用p-y曲线模型进行计算时发现,本模型收敛速度较ABAQUS 快, 在相同精度条件下, 本模型将运算时间缩短了将近60%, 可将本文提出的计算模型应用于实际工程以缩短计算时间, 提高计算效率。
3 结论
本文改进了超长桩的计算方法, 在保证计算精度的前提下提出了计算速率更快的p-y曲线模型, 分别采用数值模拟和p-y曲线模型计算在桩基顶端施加水平荷载后的桩侧土压力和桩侧水平位移, 并对两种方法的计算结果进行对比分析,得到以下主要结论:
(1) 通过数值模拟计算发现, 在桩基顶端施加水平荷载后, 桩侧土压力呈现“M” 型分布,靠近桩基侧的土压力较大, 在加载后期, “M” 型的桩侧土压力逐渐消失; 当受到水平荷载时, 桩侧水平位移随着埋深深度的增加而增加, 桩基末端的水平位移最大。
(2) 对比数值模拟结果与现场实测结果可知,通过数值模拟计算得到的桩侧土压力和水平位移与现场实测值之间的相对误差分别控制在2%和5%以内, 可根据数值模拟结果分析桩基受到水平荷载时的实际情况。
(3) 以数值模拟结果作为参照, 发现通过p-y曲线模型计算得到的桩侧土压力曲线和桩侧水平位移曲线与通过ABAQUS 软件计算得到的数值之间的相关系数分别达到0.97 和0.92; 且p-y曲线模型收敛速度较ABAQUS 快, 节约了将近60%的运算时间, 可将本模型应用于实际工程的计算,以加快计算速率, 或将本模型用以验证三维有限元软件计算结果的准确性。
