拟人机械臂关节等效的运动学映射算法

李斯雨，闵华松，王 琪

武汉科技大学 机器人与智能系统研究院，武汉 430080

随着工业技术的发展，支持操作员远程控制的协作机器人在远程医疗[1-2]、空间探测[3]、抗灾救援[4]等复杂环境下的任务都取得了一定的成果。其中机器人从人类演示中学习技能，通常比代码编程更加容易[5]。将人的动作或技能迁移到机器人身上的挑战之一是运动学映射[6]。目前根据机械臂类型不同将映射方案广义分成了两大类：人臂到工业机械臂[7]，人臂到拟人机械臂[8]。其中广泛应用的是人臂到拟人机械臂的映射，该类型系统结合了人臂的高度灵活性以及冗余七自由度机械臂的适应性。但由于人臂与拟人机械臂的结构有差异以及关节的驱动方式不同，人臂到拟人机械臂的运动学映射算法的开发较为困难。

人臂到拟人机械臂的运动学映射算法主要有基于关节空间的映射算法和任务空间的映射算法。在关节空间内，Savevska等[9]和Gong等[10]将人臂等效为七自由度机械臂，获取人臂关节位姿后，以几何方法求解人臂关节角，将拥有相同自由度的关节一一对应映射。李家霖等[11]构建手臂外骨骼，进而将人臂转换成机械臂模型，完成运动映射。将人臂等效为七自由度机械臂模型避免拟人机械臂复杂的逆运动学，具有高效的映射效率，但人臂等效为机械臂模型后丧失了人臂关节的灵活性与自由度，导致机械臂位形相似度与末端位姿精度较差。为此在相同人臂模型下，Tomić 等[12]加入关键帧数据，优化末端精度。Wang 等[13]以机械臂连杆方向与人臂的相似性，优化机械臂位形相似度，但在末端姿态上仍有较大误差。关节空间映射能直接快速完成运动学映射，但关节空间映射的人臂模型提取丧失了部分人臂运动信息，难以在末端位姿精度和位形相似度上得到良好效果。

为优化末端位姿精度和位形相似度，一部分学者在任务空间内将人臂看作整体，以人臂末端位姿和臂形建立人臂模型，并基于此完成运动学映射。Luo 等[14]通过Kinect 相机获取人臂末端坐标，建立人臂模型，采用笛卡尔阻抗控制机械臂臂形。Shi等[15]提取人臂末端的位置和姿态，并设计一种相似度控制算法筛选符合要求的机械臂逆解。然而先求机械臂逆解，后对解进行筛选，优化机械臂运动，完成映射。此类方法映射时间长，稳定性差，无法完成实时模仿。为此Li等[16]和赵京等[17]通过人臂末端位姿与臂形角，建立人臂模型，提取人臂运动特征，在机械臂逆解完成前进行约束，提高映射效率。在任务空间内，以人臂末端位姿与臂形约束建立人臂模型，完成运动学映射，具有高末端精度，但在位形相似度上表现不好，以及求拟人机械臂逆解效率低，在实时映射中机器人响应速度慢。

为了完整地将人臂运动信息传递给拟人机械臂，提高拟人机械臂末端位姿精度和位形相似度，及在拟人机械臂对人臂运动的模仿中具有较好实时性，提出了一种基于等效关节的运动学映射方法。该方法将机械臂的多个关节融合等效为人臂生理关节，使得多个机械关节在一定条件下保持约束，重点解决了人臂关节与拟人机械臂关节之间驱动方式和关节旋转轴线不同的问题，以此为基础提取人臂到机械臂的转换模型。其次针对拟人机械臂逆运动学求解复杂的问题，根据人臂到拟人机械臂的转换模型，以及球关节的关节角的集合组成ZYZ欧拉角集合的特点，将拟人机械臂运动学逆解分解成多个子问题，分别求得各关节角。为验证提出算法的性能，设计了单臂跟随实验和双臂协调实验并分别与文献[10]的基于关节空间的运动学映射算法和文献[16]的基于任务空间的运动学映射方法进行了比较。

1 拟人机械臂正运动学

为直观表示机械臂关节旋转轴线，使用旋量法对机械臂进行运动学建模，如图1 所示，S1 到S7 分别表示拟人机械臂七个关节的旋转轴线。

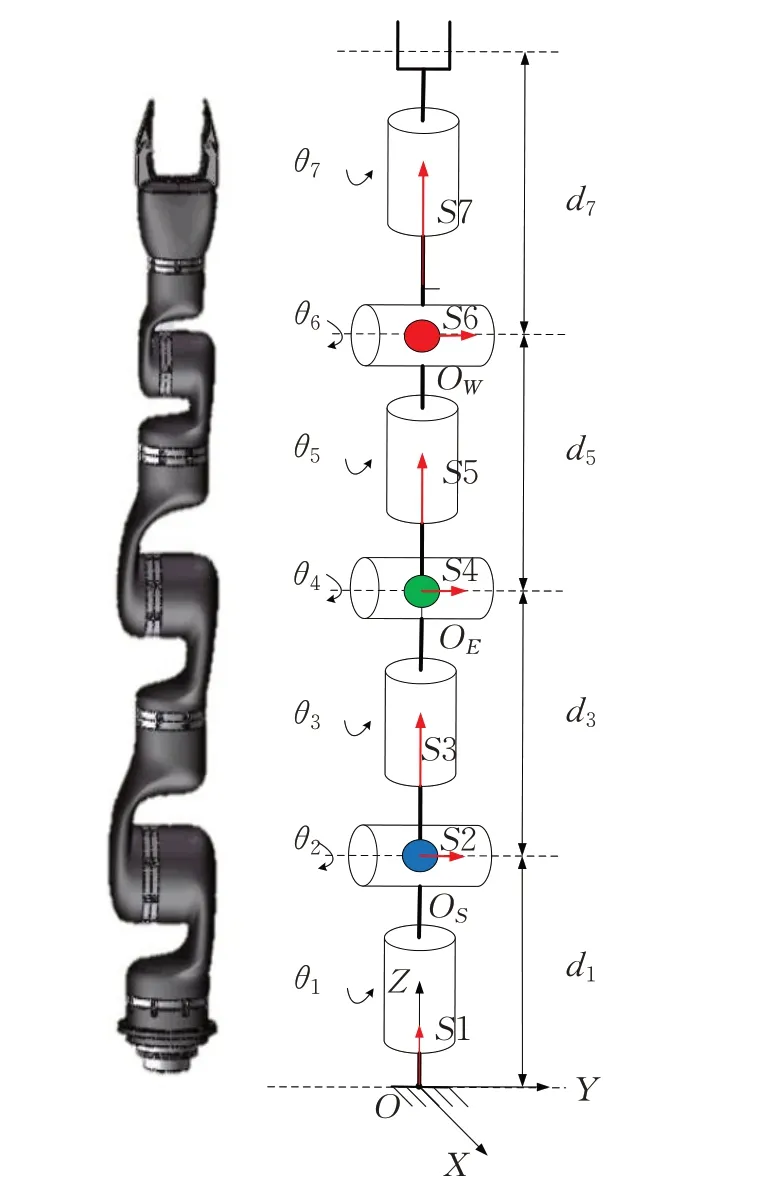
图1 拟人机械臂运动学模型Fig.1 Kinematic model of anthropomorphic robotic arm

当刚体绕某一单位矢量轴ω=[ω1,ω2,ω3]T纯转动θ角时，刚体的运动变换可以用矩阵指数形式表示：

式（1）中，为反对称矩阵：

由罗德里格斯公式可得：

式（3）中，I为单位矩阵。

拟人机械臂的运动本质上可以看成各关节的运动旋量复合而成，可以采用指数积公式进行表示：

式（4）、（5）、（6）中，gst(θ)是拟人机械臂末端位姿，为关节运动旋量，qi为关节转动位置。

联立式（4）、（5）得：

式（7）中，ωi≠0。

HR2 拟人机械臂旋量坐标ξi=[wi vi]T见表1，其中机械臂连杆长度为d1=174 mm，d3=292 mm，d5=242 mm，d7=234 mm，机械臂初始位姿gst(0)可用式（8）表达：

表1 拟人机械臂旋量坐标Table 1 Coordinates of anthropomorphic robotic arm screwtheory

2 基于等效关节的运动学映射

2.1 人臂模型到拟人机械臂模型转换

根据机器人学研究[18]，可以将人臂的小臂的旋前/旋后和腕关节的2个关节进行合并，从而在腕关节处形成一个球关节，因此人类手臂可以等效为一个S-R-S构型的七自由度机械臂，拟人机械臂和人类手臂具有相同的构型，在功能实现上能够完成人类手臂的所有动作。

人类手臂关节是靠骨骼和肌肉驱动的，以肩关节为例，肩关节以整体的形式进行运动，在完成任务时该关节自由度减少，关节旋转轴线会发生变化，如图2 所示在肩关节中心点位置建立右手笛卡尔坐标系，O为坐标原点，E点是肘关节中心点。当肘关节中心点E运动到E′位置时，在人体上表现为两个旋转轴运动，一个绕轴运动负责改变位置，一个绕轴运动负责调整姿态，其中改变位置的轴线可以随运动的改变而变化，使得人臂具有很强的灵活性。而拟人机械臂的关节转动轴线与机械结构相关，无法随任务变化，在运动中与人臂具有较大差异，给运动映射带来挑战。

图2 简化肩关节物理模型Fig.2 Simplifying physical model of shoulder joint

拟人机械臂的各个关节满足固定的运动学关系，每一个关节都是独立驱动的，可以通过合理的配合和控制来实现各个关节的联动，实现人臂到机械臂的运动映射。为完成各个关节的联合配置，暂时抛开拟人机械臂的机械结构，将其转化成三个生理关节，在生理结构上完成映射，确定拟人机械臂整体构型然后再映射回关节空间执行。定义机械臂第2个关节中心为肩关节中心，机械臂第4 个关节中心为肘关节中心，机械臂第6 个关节中心为腕关节中心。

图3 为人臂到机械臂在生理结构上的运动映射模型，SH、E H、WH和HH分别代表人臂的肩、肘、腕关节和手掌的中心，SR、E R、WR和HR分别是机械臂转化后的生理关节中心，lup和d3分别代表人臂和机械臂肩关节中心点到肘关节中心点的上臂长度，lfore和d5分别代表人臂和机械臂肘关节中心点到腕关节中心点的小臂长度，lh和d7分别代表人臂与机械臂代表腕关节中心点到手掌中心点长度。βH和βR分别是人臂与机械臂的上臂与小臂的夹角。

图3 运动学映射模型Fig.3 Kinematic mapping model

人臂运动特征函数为可用公式（9）进行表示：

式（9）中，qE、qW、qH分别是肘关节、腕关节和手掌中心的相对于肩部基坐标系的单位四元数。

将机械臂转化为生理关节后，以生理关节为映射单元，确定人臂与机械臂的比例，保证机械臂的特征姿态跟随人臂特征姿态，因此可以定义映射函数为：

式（10）中，i表示不同的关节，K为人臂与拟人机械臂连杆长度的比例，、分别表示人臂关节与拟人机械臂等效的关节的中心位置，(t)、(t)分别表示人臂关节与拟人机械臂等效的关节在某一时刻下的单位四元数。

2.2 运动映射算法

（1）坐标系转换

映射函数确定映射关系，将人臂运动信息传递给机械臂，通过映射信息求解出机械臂关节角。在机器人中间躯干建立机器人系统基坐标系{B}，同时坐标系{B}也为世界坐标系，在拟人机械臂的基座处分别建立机械臂基坐标{Rl}和{Rr}。选择在人体腰部躯干上建立人体基坐标系{HB}，以避免人上肢部分在运动过程中导致的基坐标系漂移。在人臂左肩关节中心和右肩关节中心建立人臂基坐标系{Hl}和{Hr}。坐标建立与转换关系如图4所示，下文计算均在世界坐标系{B}下完成。

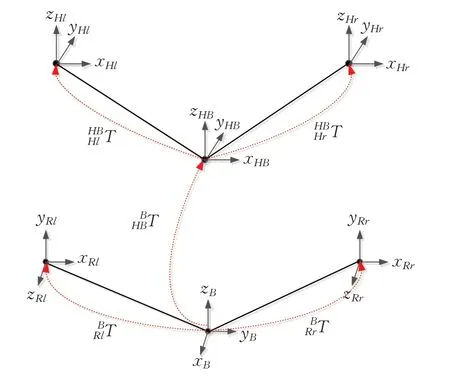
图4 人体基坐标系与基坐标转换关系Fig.4 Human base coordinate system and base coordinate conversion relationship

人体基坐标系到世界坐标系转换关系约束方程如下：

在统一基座标系下，由人臂到机械臂的转换模型可以求解出拟人机械臂的三个关节中心的位姿，因此拟人机械臂关节角可以分成子问题求解。

（2）求解θ1、θ2和θ3

肩关节决定了肘关节中心的姿态并且球形关节的关节角是构成基座标系下的ZYZ欧拉角的集合，因而可以根据肘关节中心的旋转矩阵R计算拟人机械臂的前三个关节角θ1、θ2、θ3：

式（12）是右手坐标系下单位四元数q=[w,x,y,z]到旋转矩阵的变化公式，式（13）、（14）分别表示θ2在不同的取值范围下的解。

（3）求解θ4

如图4所示肘关节只有一个自由度，通过四元数的变换即可求得肘关节夹角βR：

式（15）中Δq是在基坐标系下肘关节姿态qE到腕关节姿态qW的中间旋转变换。式（16）是单位四元数转轴角公式。

联立（15）、（16）求得βR，再由几何关系求得拟人机械臂第四关节的关节角θ4：

（4）求解θ5、θ6和θ7

由于腕关节角的配置与肩关节类似，只需求出人臂手掌旋转矩阵相对于腕关节旋转矩阵，就可由式（13）、（14）求得拟人机械臂后三个关节θ5、θ6、θ7的角度。

上述人臂到拟人机械臂的运动映射方法最多可以求出四组解，解的选取和验证在3.1.3小节详细说明。

3 实验

3.1 实验设置

3.1.1 实验平台

为验证提出映射算法，搭建遥操作系统的框架如图5所示。系统由拟人双臂机器人和惯性动作捕捉系统组成。

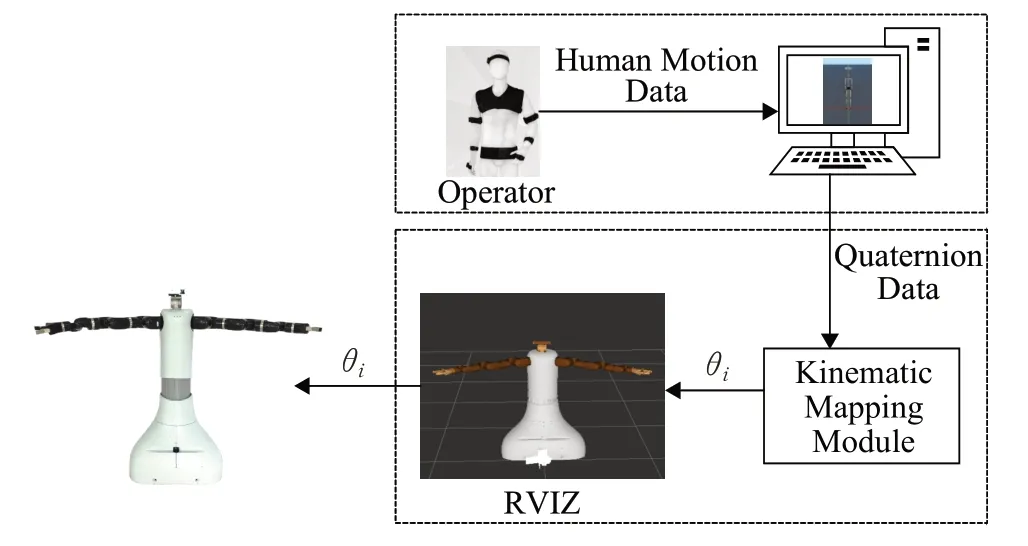
图5 实验系统结构图Fig.5 Experimental system structure diagram

3.1.2 实验流程

为验证人臂到拟人机械臂运动学映射算法的性能，设计单臂轨迹跟随和双臂协调任务实验，分别与文献[10]的运动学映射算法和文献[16]的运动学映射算法进行了对比，其中操作者的上臂和小臂参数分别为lup=280 mm和lfore=265 mm。

单臂轨迹跟随中，操作者通过手臂运动改变手臂末端位姿与姿态，拟人机械臂复现操作者手臂动作实验。双臂协调任务中，操作者控制双臂协调完成端盆，机器人实时精准复现人臂动作完成任务。

3.1.3 实验评价指标

（1）解的选取。

机械臂关节速度的限制，实验中将关节速度大于3.14 rad/s 的数据将会抛弃，因此在遥操作过程中，需要操作者对于动作速度进行控制，避免人为误差。

人臂的初始位姿及构型与机械臂的初始位姿及构型可能不尽相同，为保持运动的一致性，需要将机械臂的初始位姿和构型运动到人臂的初始位姿和构型，称该过程为映射对齐。拟人机械臂各关节转动的角度，直接反映了映射对齐的响应速度，并通过关节角度转动权重来减少靠近基座的关节运动对后面关节的影响。因此映射对齐过程需要对解进行选择，采用拟人机械臂关节转动角度的权重和进行衡量，衡量标准Mθ表达为下式：

式（18）中，ki表示机械臂各个转动关节的转动权值，由关节参数确定。θi_goal表示机械臂需要运动到的目标位姿的各个关节角，θi_ref表示机械臂初始位姿的各个关节角。

（2）位形相似度

其次通过以下标准进行评估人臂与机械臂位形相似度，在三维空间内，可将手臂到机械臂的相似程度转化成空间向量的相似度，通过拟人机械臂上臂向量和人臂上臂向量之间的夹角的均方根误差进行衡量整个运动过程的相似度。

式（19）中，d3、lup分别表示机械臂上臂和人臂上臂的方向向量，eupper(i)表示一帧动作的位形相似度。

对于小臂位形相似度衡量标准同上臂类似。从位形相似度进行约束保证机器人各个生理关节中心位置跟随人臂生理关节中心运动，同时保证机械臂末端姿态与人臂末端姿态保持一致。为直观显示，可将人臂与机械臂末端姿态转化成ZYZ欧拉角。

式（20）中，rot=α,β,γ,erot(i)表示人臂末端与机械臂末端欧拉角度的误差。

（3）运动学映射耗时时间

运动学映射方法的耗时时间包含人体数据转换时间和拟人机械臂关节角求解时间，直接影响拟人机械臂的响应速度。耗时时间采用式（21）进行计算。

式（21）中，tover为映射任务结束时间，tstart为映射任务开始时间，Sframe为数据总帧数。

3.2 实验结果

3.2.1 解的选取

一帧人臂运动数据映射到机械臂上可以求得四组解。相同的人臂位姿映射到拟人机械臂，求得四组解，其中每一组解的关节角度见表2。图6为同一个人臂动作姿态映射到拟人机械臂上，仿真得到的四种映射解。可以看到不同的解下机械臂肘关节中心的位姿和末端的位姿是相同的，而图6中虚线框标注出的拟人机械臂肩关节（图6 中蓝色虚线框）和腕关节（图6 中红色虚线框）的关节角不同。

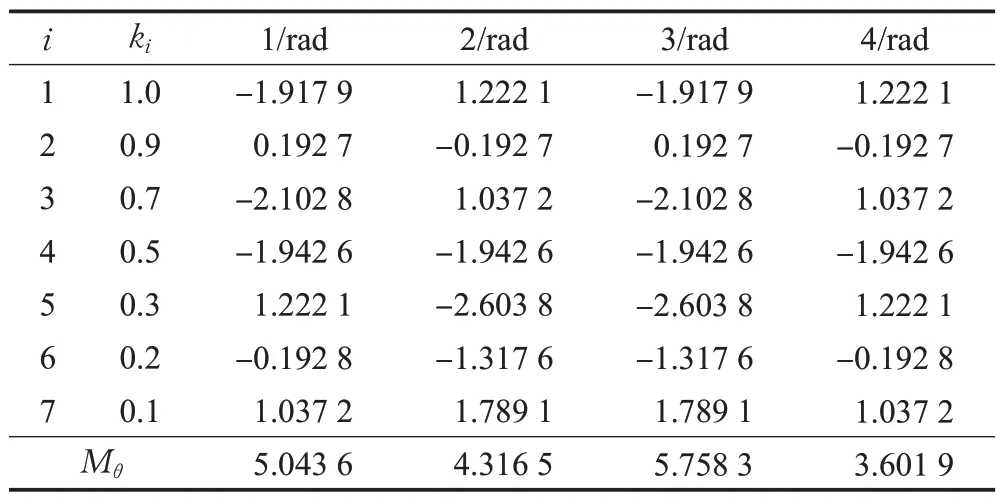
表2 不同解结果Table 2 Different results

图6 人臂位形到拟人机械臂位形的映射解Fig.6 Mapping solution of human arm bit shape to anthropomorphic robot arm bit shape

以图6为例，得到四组映射解，通过式（18）计算Mθ的值进行解的选择。首先需要人为确定ki值，其中越靠近拟人机械臂基座的关节对后面关节影响越大，其ki也越大。最终计算得到四组Mθ分别为5.043 6、4.316 5、5.758 3 和3.601 9，其中第四组解的Mθ是最小的，因此使用第四组解进行映射对齐的响应时间和关节变化幅度较少。ki的值与计算结果在表2。

3.2.2 单臂跟随实验

在单臂跟随实验中，提出方法、文献[16]方法和文献[10]方法的实验结果见图7 和表3。图8 为三种不同运动学映射方法得到的末端运动轨迹对比图。其中图（a）为三维空间下的末端轨迹对比，其XYZ轴坐标为位移；图（b）、（c）和（d）分别为末端轨迹在不同坐标轴下的投影对比，横轴坐标代表动捕数据帧数，纵坐标为不同坐标轴下的位移。从图8 中可以看出在Y轴方向上的误差比沿着X,Z方向上稍大。位形相似度上RMSEupper与RMSEfore的值为2%～4%，RMSErot小于1%，表明使用提出方法，拟人机械臂与人臂位形相似度高，机械臂末端较完美地跟踪了人臂末端姿态，提出方法成功复现了人臂动作。运动学映射消耗时间Mtime为0.082 ms。

表3 实验结果Table 3 Experimental results

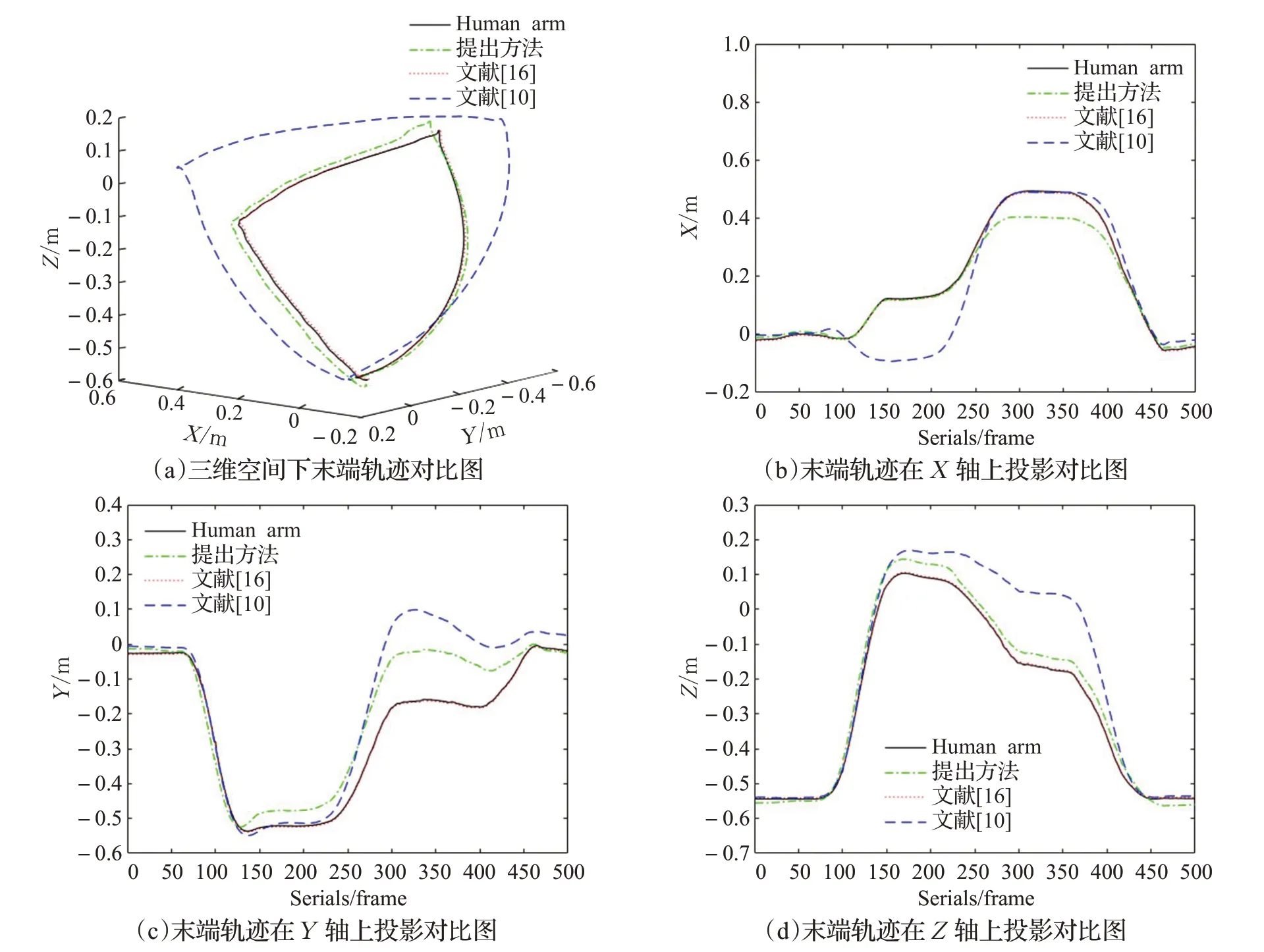
图7 人臂与拟人机械臂末端运动轨迹对比图Fig.7 Comparison of trajectory of human arm and end of robot arm

图8 遥操作双臂端盆任务Fig.8 Teleoperated dual-arms to carry basin task

文献[16]运动学映射方法，采用末端位姿和臂形角进行运动学映射，实验结果表明完美复现了人臂的位姿和末端轨迹，RMSErot小于1%，但RMSEupper与RMSEfore的值均接近20%，这意味着增加臂形角参数也无法完全保证位形相似度。其运动学映射消耗时间Mtime为0.096 ms。

文献[10]运动学映射方法，将人臂等效为拟人机械臂，并在关节空间里一一对应映射，实验结果表明，机械臂复现人臂轨迹存在一定误差，RMSErot在40%左右，RMSEupper与RMSEfore的值均接近10%，意味着末端位姿精度与位形相似度较低，其运动学映射消耗时间Mtime为0.078 ms。

由图7和表3实验结果分析得到：

在末端精度上，轨迹跟随提出方法和文献[16]方法都有良好的表现，而文献[10]方法末端轨迹精度较差。其中文献[16]方法中的末端位置轨迹是由计算误差得到的，提出方法和文献[10]方法的位置跟随误差主要是由人体运动过程中肩关节漂移带来的，可以看出提出方法肩关节漂移较文献[10]方法得到抑制。在提出方法和文献[10]方法的末端运动轨迹得到验证，在图8 子图（b）、（c）和（d）中可以看出拟人机械臂轨迹开始和终点与人臂轨迹重合，中间部分轨迹产生分离，其中文献[10]方法肩关节中心漂移未抑制，末端轨迹中间部分偏离严重。末端姿态通过RMSErot指标可以看出，提出方法和文献[16]方法产生的误差是由计算带来，而文献[10]方法丧失了末端姿态精度。

在位形相似度上，提出方法远远大于文献[10]方法和文献[16]方法，其中提出方法和文献[16]方法相比，都保持拟人机械臂臂形角与人臂臂形角一致，但文献[16]方法未对肘关节中心的姿态进行约束，使得在位形相似度上产生了较大的误差。提出方法与文献[10]方法相比，提出方法从整体出发考虑到人臂与机械臂的结构差异，文献[10]方法直接将关节一一对应映射，因此提出方法在位形相似度上优于文献[10]。

在运动学消耗时间上，运动学算法映射耗时时间与计算机性能拥有很大关系，但是在同一实验平台下，提出方法较文献[10]方法基本持平，较文献[16]方法计算效率提升了14%。其中提出方法将运动学映射问题分成三个阶段分开计算机械臂的逆解，从而避免了七自由度机械臂的逆运动学问题。实验结果表明提出的算法也具有较好的实时性。

综上所述，提出方法能够更好复现人臂的运动，计算效率高，在末端轨迹与位形相似度上，都达到了较好效果。

3.2.3 双臂协调端盆实验

完成了单臂的运动映射实验后，还进行了双臂端盆实验。实验过程如图8所示，每一步完成示意图：（a）初始位姿，（b）端上盆子，（c）端至一定高度。在运动过程中准确地复现了臂型和位姿，成功地完成了端盆任务。其中机械臂夹爪姿态复现人手掌心位姿而并非人手握取时手指姿态。

在此次任务中，统计了拟人机械臂各个关节角的变化。如图9 所示，端盆任务中双臂各个关节角变化曲线，关节角变化曲线可以看出关节运动具有连续性且平滑并且各个关节的角度变化范围都处于拟人机械臂关节可达范围中，可以有效地满足复杂任务。

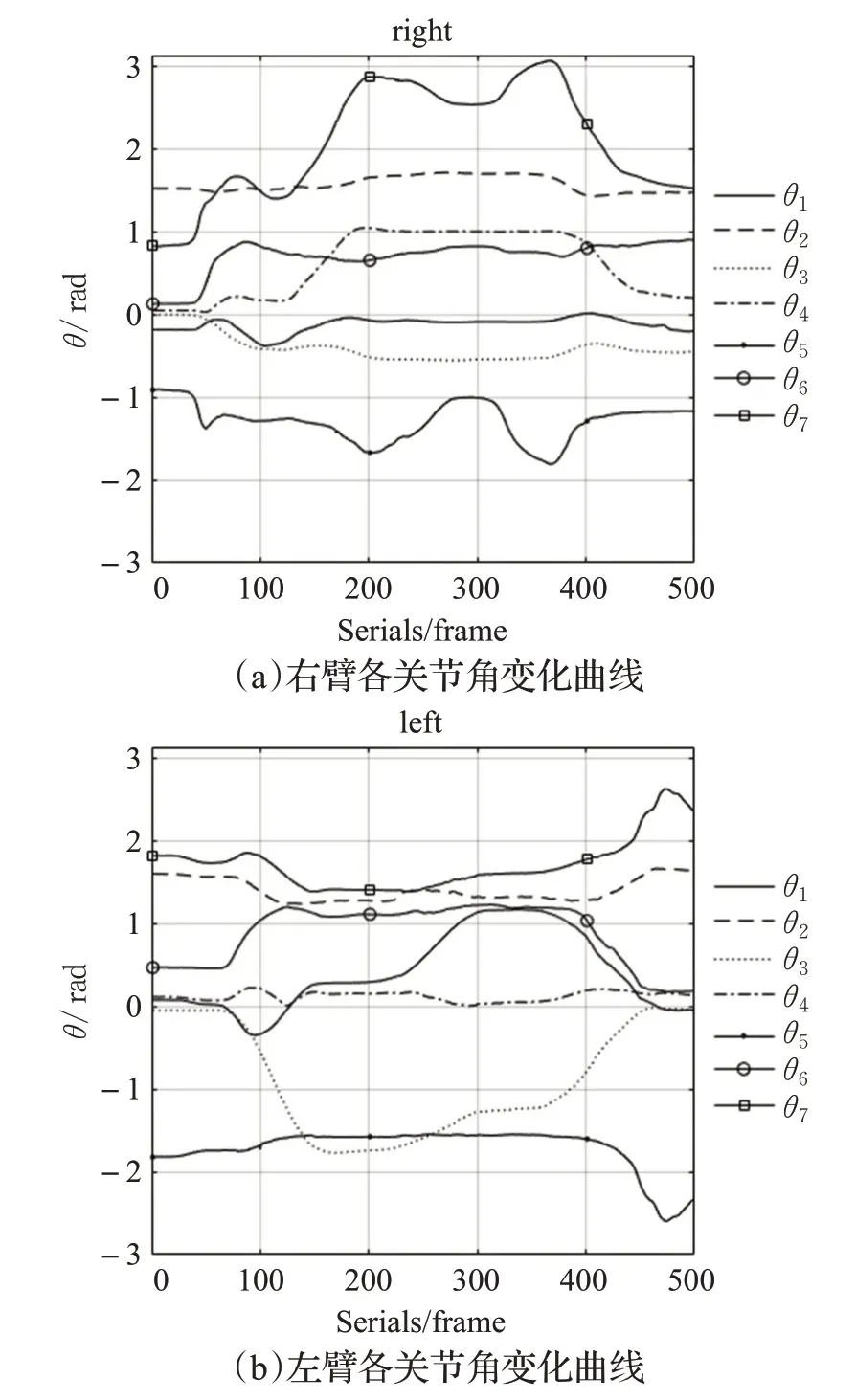
图9 双臂各关节角变化曲线Fig.9 Change curve of each joint angle of both arms

4 结束语

研究了基于等效关节的拟人机械臂运动学映射算法，该方法以人臂运动特点出发，将拟人机械臂等效为人臂生理关节，提出人臂到拟人机械臂的转换模型，重点解决了人臂关节与机械臂关节之间驱动方式和旋转轴线不同的问题。针对拟人机械臂关节角求解复杂的问题，将其分解成多个子问题，简化拟人机械臂逆运动学求解。通过仿真和实际实验表明，所提出映射算法能使操作者以更自然的方式控制拟人双臂机器人，同时机器人可以完美复现人臂动作，完成复杂的任务。

所提出方法仍然具有一定局限性，首先，未能完全通过算法抑制肩部漂移带来的误差，导致末端位姿有一定偏差。其次，可穿戴设备固定在人体表面，当操作者做一些特殊动作时，会出现传感器偏移造成误差，不能准确反映人体动作，从而造成拟人机械臂任务失败。

在未来工作中，希望设计一种更加合理的映射算法，抑制人臂运动过程中肩关节漂移带来的误差，以及更进一步将所提出算法推广到非拟人机械臂上，使其拥有更大的应用场景。