燃油喷雾碰壁数值模拟分析

秦文瑾，张雯，韩天祥，王家富

（200093 上海市 上海理工大学 机械工程学院）

0 引言

近年来，排放控制和化石能源储备成为影响内燃机技术发展方向的重要因素，尤其是在新提出的“碳达峰、碳中和”大背景下，节能减排技术成为了内燃机发展的必然趋势。燃油直喷技术作为提高发动机动力性和经济性的一种重要技术而被广泛应用。但是在直喷发动机中，尤其是小缸径发动机，燃油喷雾碰壁现象难以避免。燃油碰壁后，会附着在缸套和活塞表面，不利于燃料的充分燃烧。在燃烧过程中产生碳烟、碳氢化合物、CO 等导致排放效果变差[1]。由于发动机实际工作时缸内环境的复杂性和多变性，对于燃油喷雾碰壁现象还没有形成清晰的理论体系，因此针对燃油喷雾碰壁的研究十分必要，能够为完善燃油喷雾策略和发动机设计提供理论指导。

目前针对喷雾碰壁问题已有不少研究，周磊等[2]对定容弹中柴油的喷雾过程进行数值研究，验证了大涡模拟方法在预测燃油喷雾各项特性方面要优于RANS 模型，可以更精确地预测湍流特性，但是只具体研究了单一工况下的喷雾特性；张延志[3]构建了适用于内燃机的喷雾碰壁、油膜生成、蒸发和分离等一系列模型，对喷雾碰壁过程中存在的相关物理特性进行预测，但是忽略了碰壁过程中液滴间的相互作用；文华[4]针对燃油喷雾混合的机理进行多维数值模拟，通过对气液耦合法进行修正得出可靠的解，并与实验结果进行比较，但是没有考虑燃油喷射初期喷孔内部强烈的三维瞬态流动特征。

基于现有的研究成果，本文选择了更加精确的大涡模拟方法对燃油碰壁喷雾进行数值模拟研究，分析了不同喷射压力、环境压力及碰壁距离等多种因素对碰壁喷雾发展半径的影响。此外，还从液滴索特平均直径（Sauter mean diameter,SMD）角度直观分析了不同碰壁条件对燃油液滴碰壁破碎的影响，为后续燃油雾化、油气充分混合、提高燃烧效率以减少污染排放提供参考。

1 理论模型

1.1 喷雾碰壁模型

本研究采用Wall Film Model[5]模拟喷雾碰壁过程，图1 为液滴碰壁后运动形态示意图，液滴碰壁后可能会发生反弹、铺展、飞溅和破碎等。不同的碰壁模型对液滴的碰壁行为有不同的解释与模拟，划分液滴行为的标准也不同。

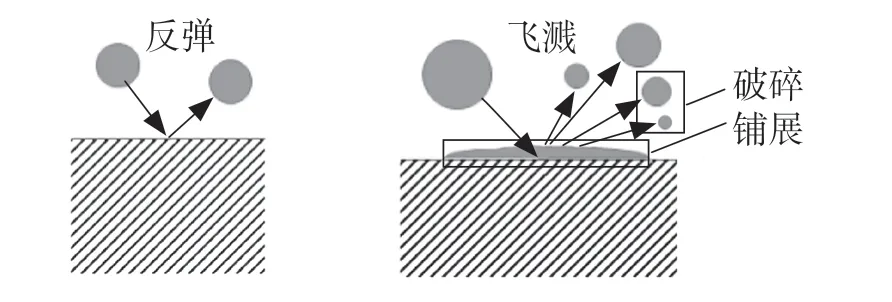
图1 液滴碰壁后运动示意图Fig.1 Schematic diagram of droplet movement after hitting the wall

Wall Film Model 根据液滴韦伯数判定是否反弹，韦伯数表达式为

式中：ρl——液滴密度；Vn——垂直于壁面的液滴速度分量；d——液滴直径；σ——液滴表面张力。

满足式（2）时液滴撞击壁面后就会发生反弹

本研究中的液滴飞溅子模型采用O'Rourke 模型，飞溅判据综合韦伯数、液膜厚度和粘度，用E2表示这3 个因素的综合作用，当满足式（3）时液滴/液膜就会发生飞溅。

式中：ha——局部液膜厚度；d——碰撞液滴直径；δbl——边界层厚度；O'Rourke 和Amsden 根据Mundo 等人的实验工作，提出=3 330。

式中：μl——液滴粘度。

1.2 大涡模拟数学模型

大涡模拟采用空间平均的方法，通过过滤函数将湍流场分解为可求解的大尺度量和不可直接求解的小尺度量，大尺度量与流场初始条件及边界条件相关，具有各向异性的特点，可直接求解瞬时三维湍流方程组获得；而小尺度量由粘性力产生，且各向同性，不可直接求解。大涡模拟对大尺度涡团的运动进行显示求解，是一种求解非稳态问题的方法，同时能够捕捉到湍流涡团的小尺度随机结构，使得对湍流特性的模拟更为精准。为使控制方程组封闭，必须建立关于亚网格应力的数学模型。本研究采用亚网格动态模态模型，该模型不使用湍流粘度模拟亚网格应力张量，而是将亚网格应力表示为一个张量系数与亚网格湍动能的函数式

式中：cij——张量系数；k——湍动能。

2 计算模型建立

Zhang 等[6]使用定容弹模型研究了喷射压力、碰壁距离等条件对碰壁射流演化和壁面液膜动力学的影响；Pan 等[7]利用激光诱导荧光、Mie 散射等光学诊断技术，捕捉喷雾碰壁过程的宏观行为，得到了相应工况下的碰壁喷雾发展特性数据。本研究基于Zhang 等[6]和Pan 等[7]的喷雾碰壁实验建立计算模型，选取的实验参数如表1 所示。

表1 碰壁喷雾实验参数Tab.1 Experimental parameters of wall impinging spray

本模拟采用的定容弹模型计算网格加密策略除了采取速度自适应加密、喷孔加密外，还在喷雾碰壁区域上添加了碰壁边界加密和喷雾卷吸区域的固定加密。文献[6]的垂直喷射实验喷射燃料为柴油，文献[7]的实验喷射燃料为异辛烷，本文模拟所用的模型设置为上壁面半径为10 mm，下壁面直径为30 mm，碰壁距离分别为30、40、50 mm 的3 个圆台型定容弹，其他的喷嘴直径、环境压力及温度、喷射条件等计算参数均与实验保持一致。

3 结果分析

3.1 喷雾碰壁模拟结果验证

（1）网格无关性验证

在进行模拟结果的对比分析之前首先进行网格无关性验证。使用不同的网格加密策略模拟了文献[6]的垂直喷射实验中喷嘴直径为0.135 mm、喷射压力为50 MPa、环境压力为0.1 MPa、碰壁距离为40 mm 的工况，并将模拟结果与实验数据进行对比。粗网格加密策略的最大网格数为250 万，最小网格尺寸为0.2 mm；细网格加密策略最大网格数为300 万，最小网格尺寸为0.1 mm。图2 是粗细2 种网格加密策略下模拟的喷雾发展半径随时间的变化情况，可以发现在各时刻2 种策略模拟的喷雾发展半径差别不大，并且二者的曲线发展趋势吻合度也较高，因此认为2 种加密策略模拟的喷雾半径接近一致。网格无关性得到验证，在保证足够计算精度的同时减少模拟时间。

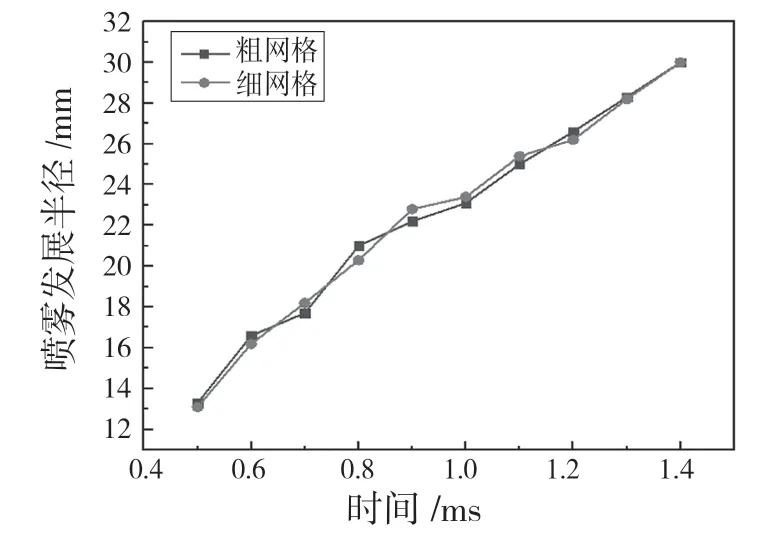
图2 不同网格加密策略下模拟的喷雾发展半径Fig.2 Simulated spray development radius under different mesh refinement strategies

（2）碰壁模型验证

在对喷雾碰壁特性及其影响因素进行研究之前需要验证所选碰壁模型的合理性。根据文献[6]的垂直喷射实验和文献[7]的60°斜喷实验的实验条件及工况建立模型，设定网格加密策略的最大网格数为2.5×106，最小网格尺寸为0.2 mm，通过对比模拟结果和实验数据验证模型的准确性。

图3 是文献[6]的垂直喷射实验测得的喷雾形态和模拟的碰壁喷雾液滴空间分布形态的对比，从喷雾的宏观形态上看，模拟的液滴空间分布与实验结果十分接近，碰壁模型较好地再现了喷雾碰壁后的径向发展和轴向卷吸过程，表明模型对碰壁喷雾的模拟从整体符合实际情况。

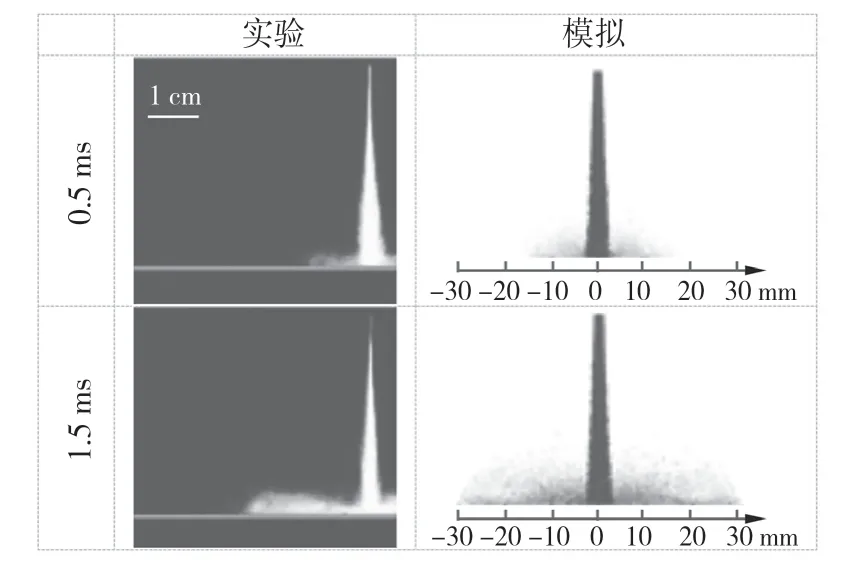
图3 碰壁喷雾投影与模拟的喷雾液滴空间分布图Fig.3 Projection of spray impringing on wall and spatial clistribution of simulated spray droplets

图4 是文献[7]的60°斜喷实验的不同时刻碰壁喷雾形态与模拟的碰壁喷雾液滴空间分布形态的对比，从喷雾发展的形态上看，不仅是喷雾的整体宏观形态较为一致，而且很好地呈现出喷雾碰壁后发生的液滴反弹、飞溅破碎等微观特性。对比2 组实验结果与模拟结果，可以认为所选碰壁模型较为准确地描述了喷雾碰壁过程的发展状况。

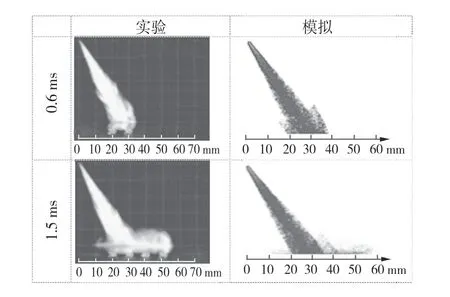
图4 碰壁喷雾投影与模拟的碰壁过程喷雾散点图对比Fig.4 Comparison of spray projection and simulated wallcollision process spray scatter plot

3.2 不同条件对碰壁喷雾发展的影响

使用已验证的碰壁模型模拟不同喷射压力、环境压力及碰壁距离下的喷雾碰壁过程，对不同条件下的碰壁喷雾特性进行研究，探究对碰壁喷雾发展的影响，结果如图5 所示。由图5（a）可以明显看出，喷射压力为100 MPa 的喷雾发展半径始终大于50 MPa 的喷雾发展半径，但是随着时间的推移，二者的差距逐渐减小。这可能是因为碰壁初始时刻100 MPa 的碰壁喷雾携带的动能更多，碰壁后发展较快；但是速度越快，受到周围空气阻力也越大，因此喷雾发展半径的发展趋势减缓，表现为随时间推移与50 MPa 碰壁喷雾发展半径差距逐渐减小。

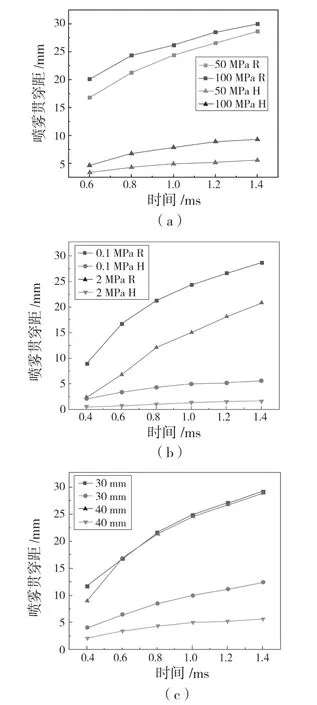
图5 不同条件下模拟的碰壁喷雾贯穿距随时间的变化Fig.5 Variation of wall-impacting spray penetration distance simulated with different conditions

图5（b）是其他条件相同只改变环境压力的碰壁喷雾发展半径及卷吸高度随时间变化曲线，可见，增大环境压力使得发展半径和卷吸高度均减小，原因在于较大的环境压力给予喷雾射流发展更大的阻力，限制其发展；图5（c）是不同碰壁距离的喷雾发展半径及卷吸高度随时间变化曲线，可以看出，碰壁距离减小，喷雾发展半径有所增大，但在初始时刻增大较明显。原因为碰壁距离减小，意味着喷雾自由射流阶段时间减少，在此期间的动能损失较少，碰壁后的动能较大，因此碰壁初始时刻发展半径有较为明显的增大特点。碰壁喷雾继续沿径向发展，由于其速度较快，受到周围空气阻力作用较大，损失的动能增加，因此发展速度降低，随后二者的发展半径在各时刻下差别不再显著。

3.3 碰壁喷雾粒径变化规律

从喷雾SMD 角度分析碰壁喷雾发展特性，不同条件下喷雾SMD 随时间的变化曲线如图6 所示。由图6（a）可见，不同喷射压力下的SMD 随时间的变化走势相似，即初期迅速减小、中期减小速率放缓并呈阶梯式下降、后期趋于稳定。SMD 发生阶梯式下降是因为此时喷雾开始碰壁，更多的液滴撞击壁面后飞溅破碎。此外，100 MPa 喷射压力下的喷雾SMD 始终小于50 MPa，且其率先发生阶梯式下降现象一方面是因为喷射压力增大而环境压力不变，更大的压差使喷雾射流速度变大，空气阻力相应变大，液滴破碎更加剧烈，碰撞韦伯数变大，低韦伯数液滴增加，碰壁后发生反弹，高韦伯数的液滴具有相对较大的动量，碰壁后飞溅破碎也相对更剧烈；另一方面是随着喷射压力增大，喷雾射流速度增大，使得液滴碰壁后飞溅反弹更剧烈，液滴间碰撞融合反向分离的频率变大，从而促进了SMD 的减小。

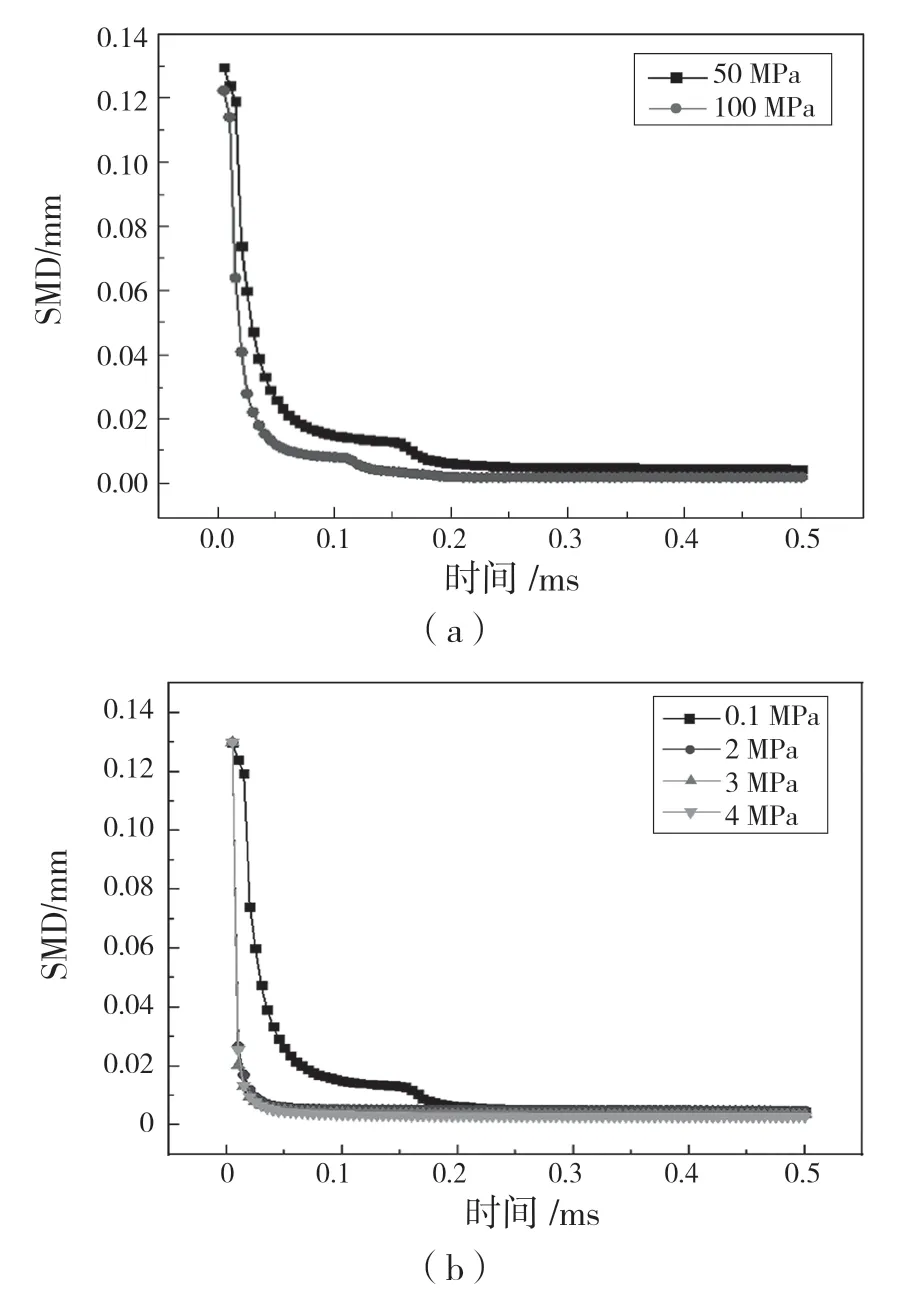
图6 不同条件下喷雾SMD 随时间的变化Fig.6 Variation of spray SMD with time under different conditions

从图6（b）可以看出，环境压力增大后SMD变化规律与0.1 MPa 时有较大区别。首先在喷雾碰壁前，环境压力增大的喷雾SMD 迅速减小并达到稳定；其次增大环境压力后，SMD 变化曲线没有了碰壁时的阶梯式下降阶段，且环境压力为2、3、4 MPa 下的SMD 曲线几乎完全重合，这可能是由于环境压力越高，定容弹内的空气密度越大，对燃油喷雾发展的阻力增大，燃油喷雾束与空气的相互作用也增强，有利于喷雾液滴破碎；另外由于定容弹内气动阻力增大，喷雾射流速度相对减小，碰撞韦伯数降低，致使产生更多的高韦伯数液滴撞击壁面发生飞溅破碎行为，使得SMD 减小。此外，较大的环境压力使喷雾在到达壁面前已损失更多的动能，再加上SMD 在碰壁前已经大大减小，二者共同作用使得碰壁后再飞溅破碎的可能性减小，因此不再出现喷雾SMD 在碰壁时阶梯式下降现象。图6（c）为不同碰壁距离的喷雾SMD 随时间的变化曲线，可以看出，喷雾在碰壁时SMD 均呈现阶梯式降低随后达到稳定，区别在于碰壁距离越近，碰壁时刻越早，SMD 曲线发生阶梯式下降的时刻也越早；此外，还可发现随着碰壁距离增大，下降曲线逐渐平缓，SMD 减小的速率逐渐降低，这可能是因为碰壁距离越小，喷雾到达壁面时携带的动能越多，碰壁后发生飞溅、破碎的速度也越快，从而使SMD 下降更快。最后，不同碰壁距离的喷雾SMD 均达到了比较接近的稳定值，说明碰壁距离对碰壁之后最终稳定状态的SMD 影响不大。

4 结论

本研究采用大涡模拟方法对碰壁喷雾进行数值模拟，研究喷雾与壁面的相互作用特性。对比了不同喷射压力、环境压力及碰壁距离对喷雾碰壁后的影响，此外，还从SMD 角度分析了不同碰壁条件下的碰壁喷雾特性，得出如下结论：

（1）喷射压力从50 MPa 增大到100 MPa 时，碰壁喷雾的发展半径和卷吸高度均有所增加，但是随着时间推移，其增大的趋势逐渐减小；环境压力从0.1 MPa 逐渐增大到4 MPa 时，碰壁喷雾的发展半径及卷吸高度均有所减小，并且这种减小的趋势并不随着时间的推移而改变；碰壁距离从50 mm逐渐减小到20 mm 时，碰壁喷雾的卷吸高度明显增大，而发展半径只在碰壁后初始阶段有所增大。

（2）喷射压力从50 MPa 增大到100 MPa 时，碰壁喷雾SMD 减小；增大环境压力，削弱了碰壁行为对SMD 的减小作用；碰壁距离越远，碰壁发生的时间越晚，但是并不影响碰壁之后最终稳定状态下的SMD。