开放实验室内部网络非法入侵准确检测仿真
2023-10-29吴延慧杨凌凤
吴延慧,杨凌凤
(南通大学信息化中心,江苏 南通 226019)
1 引言
在网络技术飞速发展的背景下,各种网络安全事件日益频发,使得信息安全受到人们的高度重视,如何有效确保网络安全是十分重要的[1-2]。在各个高校极力推广开设开放式实验室的情况下,如何确保实验室信息的安全性成为当前研究的热点话题。
国内相关专家对网络非法入侵检测方面展开了大量研究,例如芶继军等人[3]通过随机森林算法构建网络入侵检测模型,利用该模型完成网络攻击检测。张安琳等人[4]采用SMOTE-Tomek算法对数据集平衡处理,通过特征重要性算法完成特征选择;将CNN和BiGRU模型融合处理,同时引入注意力机制提取入侵特征,实现网络入侵检测。马泽煊等人[5]对数据展开独热编码和归一化处理,采用WaveNet执行卷积操作,对数据序列缩短处理,同时提取网络入侵特征,采用BiGRU完成模型的训练以及分类处理工作。在以上几种网络入侵检测方法的基础上,本文提出一种开放实验室内部网络非法入侵检测方法。经实验测试证明,所提方法不仅可以获取高精度的检测结果,同时还能够有效降低误检率,具有良好的适应性。
2 非法入侵检测方法
2.1 建立非法入侵检测模型
RBF神经网络属于前向神经网络,可以利用学习或者任意精度逼近非线性函数,全面提升收敛速度,被广泛应用于网络入侵检测中[6-7]。通过REF神经网络构建开放实验室网络非法入侵检测模型的核心部分,主要由三个不同的部分组成,如图1所示。
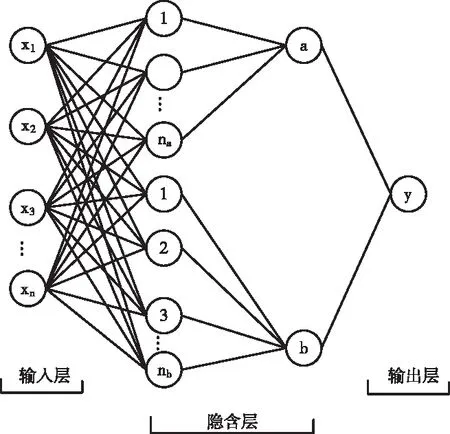
图1 RBF网络结构
将KDD99数据集特征向量作为RBF神经网络的输入向量,经过隐含层径向基神经元的非线性映射,将输入向量映射到高维空间内。径向基神经元主要是由两种不同类型的神经元组成,分别为正常类神经元和异常类神经元。
在传统的RDF神经网络中隐含层单纯采用径向基神经元。对于单一样本的分类准确率偏高。但是输入复杂的样本类别后,总体的准确率还需要进一步提升。所以,需要将改进的RBF网络应用到开放实验室内部网络非法入侵检测中[8-9],详细的入侵检测模型架构如图2所示。
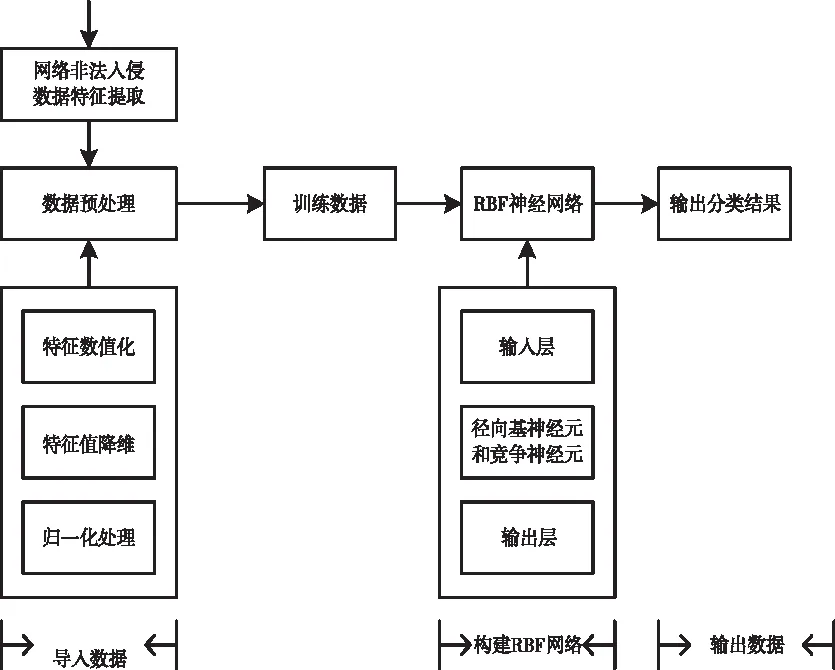
图2 非法入侵检测模型架构图
经过上述分析,引入RBF神经网络构建开放实验室内部网络非法入侵检测模型[10-11],详细的操作步骤如下所示:
1)优先输入神经网络输入向量和期望输出向量。其中,输入向量主要包含建立网络时的训练样本以及仿真测试时的测试样本。将全部样本归一化处理,经过归一化处理的样本XX可以表示为式(1)的形式:
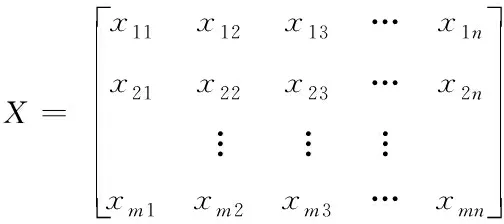
(1)
2)输入向量利用输入层直接传递到隐含层,同时对径向基神经元节点中心初始化处理,设定阈值的取值范围;其中,输入层的节点数即为样本向量的特征值总数。
在获取RBF神经网络中的特征值总数后,还需要进一步计算输入向量和隐含层节点中心两者之间的距离D(xi,cj),即欧式距离,如式(2)所示:
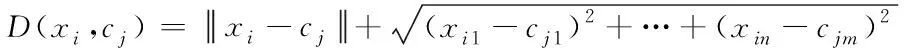
(2)
式中,xin代表特征空间内各个节点之间的距离;cjm代表各个径向基节点之间的距离。
通过非线性的径向基函数展开计算,计算随机一类数据出现的概率。设定径向基向量为S={s1,s2,s3,…,sm},m代表径向基神经元的总数,径向基层节点对应的输出可以表示为式(3)的形式:
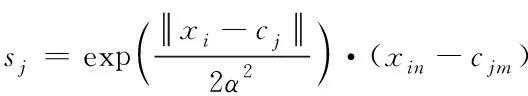
(3)
式中,sj代表径向基函数;α2代表高斯函数的方差。
隐含层第二层为竞争神经元,神经元的数量为样本数据的种类数,在两种不同类型的神经元中,每个神经元只和自身类别相同的上层神经元连接,同时各个神经元只需要计算相同样本输出值的加权即可。利用式(4)给出输入向量属于正常类的概率ρ(x|E(a)):
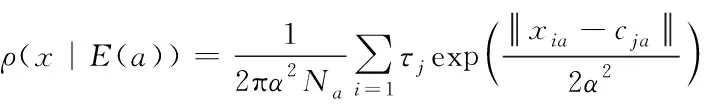
(4)
式中,Na代表正常类样本总和;τj代表网络输出特征。
输入向量属于异常类的概率ρ(x|E(b))如式(5)所示:
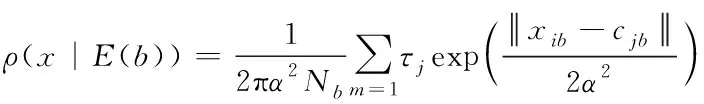
(5)
式中,Nb代表异常类样本总数。
3)对隐含层权值优化处理,具体操作步骤为:
①将隐含层中的参数集合设置为空,随机形成未成熟的参数集合,同时将对应的适应度取值设定为0;
②判断集合中各个参数的取值是否大于适应度,同时选取取值最高的参数建立参数集合,实现隐含层权值优化。
4)采用优化处理之后的参数建立基于RBF的开放实验室内部网络非法入侵检测模型ΔHx,y,如式(6)所示:
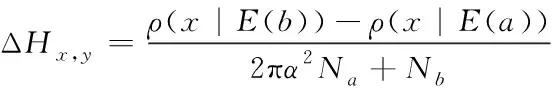
(6)
2.2 网络非法入侵检测模型求解
根据2.1节建立的网络非法入侵检测模型,采用自适应蛙跳算法对该模型求解。对于d维问题而言,初始群体是由一定数量青蛙随机形成的,根据种群类型将群体划分为s个种群,每个群体是由n只青蛙组成,在第1个群体内放入第1只青蛙;第s群体内放入到第s只青蛙,以此类推,直至全部青蛙完成分配处理。
在每个子群中,设定Xb代表适应度取值最佳的青蛙;Xw代表适应度取值最差的青蛙;Xg代表种群内适应度取值最佳的青蛙;完成上述操作后,对各个种群展开局部搜索处理,同时在迭代过程中只更新适应度取值最差的青蛙,则对应的更新策略Di如下所示:
Di=rand(Xb-Xw)
(7)
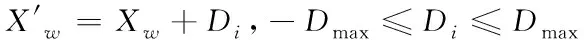
(8)
式中,rand()代表在0~1之间的随机数;Dmax代表青蛙在设定范围内的最大可移动距离。
自适应蛙跳算法主要通过青蛙的觅食行为展开协同优化处理,将全部青蛙划分为多个不同子群,利用各个子群实现消息的传递。另外,还需要将子群进化和全部交换两者有效结合,确保算法的性能得到有效优化。经典蛙跳算法主要划分为以下几个阶段[12],分别为:
1)种群初始化:
随机形成初始解集中的N个候选解,同时将N个候选解平均划分到多个不同的子群中。
2)子种群进化:
将全部青蛙划分为多个不同的子群,对于每一个子种群而言,通过最优适应度函数的候选集Sb对最差适应度的候选集Sm展开更新,对应的更新公式如下:
S*=Sm+U(Sb-Sm)
(9)
式中,S*代表全新候选集;U代表随机数。
3)全局交换:
当全部子群完成步骤2)的操作之后,经过混合计算获取全部候选集,将适应度按照从小到大的顺序排列,同时执行子种群划分,跳转至步骤2)重复上述操作。
为了有效改进经典蛙跳算法[13-14]存在的不足,本文对自适应蛙跳算法进行分析,使其可以获取更加满意的检测效果。重点需要针对以下两方面内容展开分析:
1)自适应变异操作:
经典蛙跳算法寻优过程是十分复杂的,且寻优性能也并不理想。为了有效解决上述问题,引入变异操作可以有效改进候选编码和解码的结构,确保各个子群的多样性,同时还可以解决经典蛙跳算法陷入局部最优的情况。
另外,在自适应调整中主要包含交换以及插入等相关操作,在各种优化算法中均得到应用。所以,在经典的蛙跳算法内加入自适应变异操作,确保算法的综合性能得到有效提升。
2)通过层次分析方法调整不同影响参数权重:
利用层次分析法调整经典蛙跳算法各个参数的取值,详细的操作步骤如下:
1)优先构建判断矩阵C,如式(10)所示:

(10)
在自适应蛙跳算法中,各个参数的相对权重表示为式(11)的形式:

(11)
式中,ωij代表参数的相对权重取值;kij代表各个因素的重要性程度值;qij代表种群中个体的最佳变异概率。
2)依据式(11)计算得到的参数相对权重,建立判断矩阵R,即:

(12)
利用式(12)中获取的判断矩阵调整各个参数的概率,对各个青蛙子群的分布情况展开分析,同时将不同子群参数应用到相同的集合内,引入德尔菲法调整全部参数的评分。提取不同评估参数的特征,采用集合构建模糊集,进而经过计算得到隶属集合L,如式(13)所示:

(13)
3)通过式(14)进一步获取对应的隶属度函数,即:
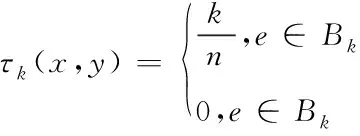
(14)
式中,τk(x,y)代表模糊隶属度函数;e代表随机常数。
采用自适应蛙跳算法对开放实验室内部网络非法入侵检测模型求解,操作步骤为:
1)设定自适应蛙跳算法中的参数取值。
2)随机形成多个候选集,进而建立对应的初始解集V,如式(15)所示:
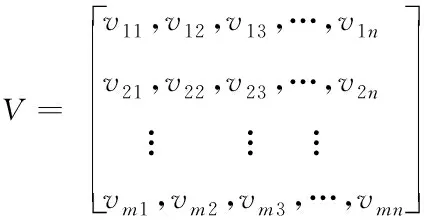
(15)
3)计算子群中不同个体的适应度取值Fm:
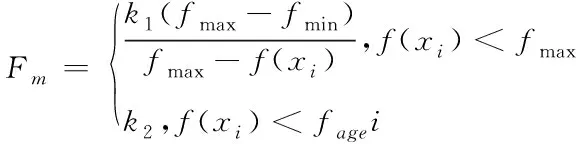
(16)
式中,fmax、fmin和fage分别代表最大、最小以及平均适应度值;f(xi)代表第i只青蛙的适应度取值;k1和k2均为常数。
4)对全部候选集合执行变异次数,同时判断是否大于最大搜索次数,假设是,则继续执行下一步骤;反之,则返回至步骤1)。
5)将适应度按照从小到大的顺序排序,完成子群划分。
6)通过自适应蛙跳算法对网络非法入侵检测模型求解,实现最终检测[15]。
3 仿真研究
为了验证所提开放实验室内部网络非法入侵检测方法的有效性,进行实验研究。实验数据集来自KDD99数据集,该数据集中包含多种不同类型的攻击。利用表1给出数据样本的分布情况:
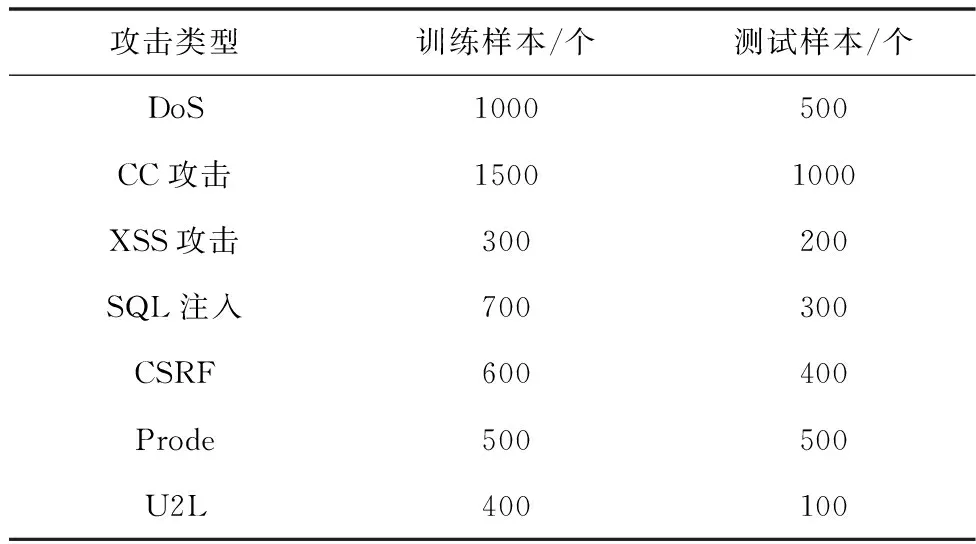
表1 样本分布情况
为了确保实验结果的可比性,实验选取两种传统方法作为对比方法,分别为文献[3]方法和文献[4]方法,测试指标主要包含检测率和误检率,对应的计算式如下:

(17)

(18)
利用图3和图4分别给出各个方法的检测结果:
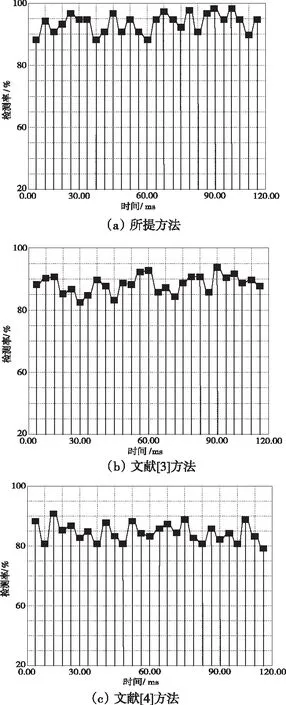
图3 不同方法的检测率测试结果对比
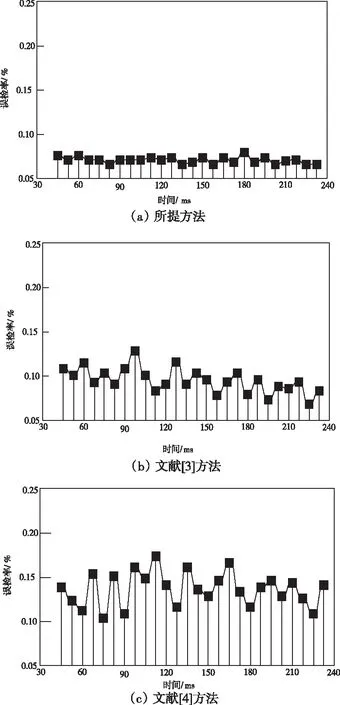
图4 不同方法的误检率测试结果对比
分析图3和图4中的实验数据可知,采用所提方法开展开放实验室内部网络非法入侵检测时获取的检测结果更加精准,而另外两种方法的检测性能明显不如所提方法,全面验证了所提方法的优越性。原因在于所提方法在经典蛙跳算法的基础上引入变异操作,不仅可以确保各个子群的多样性,同时还可以解决经典蛙跳算法陷入局部最优的情况,有利于提升入侵检测效果。
4 结束语
检测开放实验室内部网络是否存在非法入侵具有十分重要的研究意义,为了得到更加精准的网络非法入侵检测结果,提出一种开放实验室内部网络非法入侵检测方法。经过实验测试证明,采用所提可以更好完成实验室内部网络非法入侵检测,确保实验室的稳定运行。由于在构建入侵检测模型中涉及大量参数,没有考虑合适参数的选择问题,为了进一步提升所提方法的优越性,后续将引入相关方法确定最优参数。
