一种基于灰色理论的制导系统评估方法研究
2023-10-29李迎博谭黎立
李迎博,谭黎立,梁 卓,胡 骁
(中国运载火箭技术研究院,北京 100076)
1 引言
近几十年来,系统评估方法有了很大发展,各种评估方法已达数百种之多,这些评估方法都有其不同特点,在运用中也有各自的使用范围和利弊。常用的评估方法一般分为三类:定性评估法、定量评估法及定性定量综合评估法。
定性评估法主要依靠评估人员的经验和逻辑判断能力,主要有德尔菲法和专家评议法[1]。定性评估法可以充分发挥人的主观能动性,但对评估中的诸多影响因素难以全面表达;定量评估法是将统计数据作为依据,按照指标体系建立数学模型,依靠计算机或数学手段求得评估结果,常用的有主成份分析法[2]、数学分析法等。定量分析法完全以客观数据为评价标准,可靠性高,但评估对象往往过于复杂,不利于推广应用;定性定量综合评估法吸取上述两种方法的优点,融合数学分析与专家意见,应用较为广泛,常用的包括层次分析法[3]、模糊综合评价法[4]以及灰色系统理论法[5]。
本文以爱国者-3防空导弹为研究对象,建立了其制导系统性能评估指标体系,并采用了一种灰色系统理论与层次分析法相结合的评估方法进行性能评估,实际计算结果证明了指标体系与方法的合理性。
2 制导系统性能评估指标体系建立
影响制导系统性能的因素由很多,包括制导算法能力、战术指标满足性、过程约束等,本文从制导律性能、战术指标和其它性能指标三方面选取底层指标元素。
2.1 制导律性能
防空导弹的制导律一般分为中制导、末制导及中末交班规律三段,中制导负责将导弹导引至预测命中点,末制导直接导引导弹命中目标,中末交班规律负责二者之间的指令过渡。制导律性能主要要素包括最大需用过载、作战空域、适应目标机动的能力、计算量等。
● 最大需用过载
最大需用过载是导弹必须考虑的技术指标,飞行过程中的过载指令一般由制导算法给出。
● 最大航程、最大射高
为导弹重要技术指标,描述了制导律的基本性能。
● 适应预测命中点误差的能力
由于预测命中点是根据目标当前状态外推得到,因此存在一定的误差,制导律需适应这种误差。
● 适应目标机动能力
目标在进行机动突防或逃逸时,导弹制导律需有对应的策略。
● 技术实现难易程度
制导律引入实际应用中的难度。
● 制导律计算量
制导律单周期最大计算耗时,需与弹上计算能力相匹配。
2.2 战术指标
战术指标由导弹总体性能决定,与制导系统相关的主要包括如下内容。
● 燃料消耗
由于导弹燃料有限,因此导弹制导系统计算出的飞行轨迹需尽量减少燃料消耗。
● 姿态角变化量
为减少控制系统控制难度,制导系统给出的姿态角指令不能变化过大。
● 碰撞点交会角
交会角是指导弹速度矢量与目标速度矢量之间夹角的补角,由于交会速度往往比较大,因此碰撞点交会角的大小对拦截效果有很大影响。
● 飞行时间
飞行时间是指导弹从发射到命中的时间,飞行时间的长短会影响燃料消耗,制导系统规划出的飞行轨迹需考虑飞行时间的长短。
● 碰撞速度、命中精度
碰撞速度和命中精度直接决定了拦截威力,也是衡量制导系统性能的关键指标。
2.3 其它性能指标
其它性能指标主要考虑飞行安全性、可靠性相关的指标,本文选取飞行过载约束项。
由此可得到制导系统性能评估指标体系如图1所示。
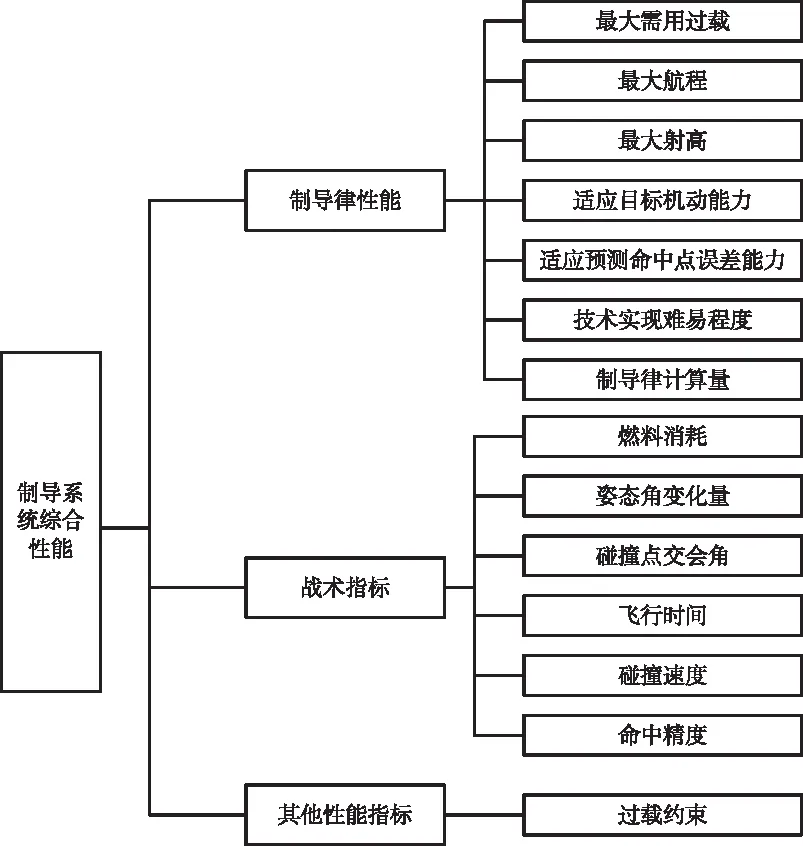
图1 制导系统性能评估指标体系
3 指标权重计算
本文使用应用最为广泛的层次分析法确定底层指标权重,具体步骤如下。
3.1 建立判断矩阵
根据指标之间的相对重要性,分别建立次层指标对顶层指标的判断矩阵A、底层指标对对应三个次层指标的判断矩阵B1、B2、B3。结果如下
B3=[1]
3.2 判断矩阵一致性校验
对上述四个判断矩阵A、B1、B2、B3进行一致性校验,得到的一致性指标如下
CIA=0.0012
CIB1=0.1032
CIB2=0.0091
CIB3=0
一般一致性指标临界值与判断矩阵阶数n有关,具体取值如表1所示。
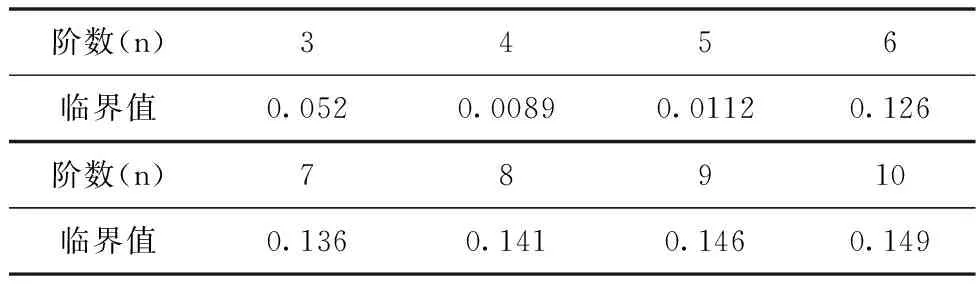
表1 一致性指标临界值
可见四个判断矩阵一致性指标均小于临界值,一致性校验通过。
3.3 相邻层指标权重向量计算
依据判断矩阵,使用对数最小二乘法求取权重向量,即对矩阵按行元素求积后,再求1/n次幂(n为矩阵阶次),最后进行归一化处理。
可得到判断矩阵对应的权重向量,结果如下
3.4 底层对顶层指标权重向量计算
首先,根据前文计算得到的各层权重向量描述底层指标对次层指标的组合权重,结果如下
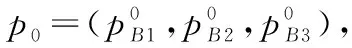
p=p0·pA
(1)
依据公式,计算得到底层指标对顶层指标的权重向量为
p=[0.1030 0.0478 0.0478 0.0918 0.1622 0.0259 0.1030 0.0257 0.0525 0.0525 0.0257 0.0850 0.0675 0.1095]T
4 灰关系系统评估
制导系统综合性能指标由底层指标评估值及底层指标对顶层指标的权重向量决定。对于底层指标的评估一般分为理论评估和人为评估两种。理论评估为建立底层指标评估相关的数学模型,严格按照指标数值计算得到评估值,但这种方法对数学模型要求过于苛刻,例如姿态角变化量、技术实现难易程度等,很难给出具体的评估模型;人为评估可以充分发挥评估专家的专业优势,但单名专家的评估往往主观性较强,而多名专家评估时,不可避免会存在一定的分歧,导致评估不准确甚至失败。
灰关系系统评估法是灰色系统理论与层次分析法结合的一种评估方法。它主要解决的是底层指标对顶层指标权重向量确定后,如何利用数学的手段综合多名专家的意见,完成对底层指标的评估,进而得到顶层指标的评估值。具体方法见下文。
4.1 评价灰类及白化权函数确定
定义灰关系系统中的指标评估分级,具体见表2。

表2 灰关系指标评估分级
对应的灰数和白化权函数如下:
第一灰类“优”,其白化权函数为f1(x);
第二灰类“良”,其白化权函数为f2(x);
第三灰类“中”,其白化权函数为f3(x);
第四灰类“差”,其白化权函数为f4(x)。
白化权函数以分段函数表示,见表达式(2)-(5)。
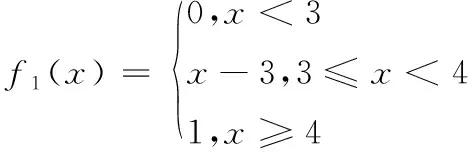
(2)
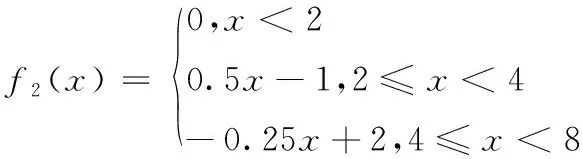
(3)

(4)
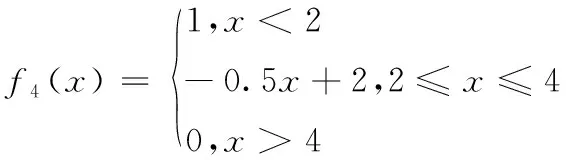
(5)
4.2 评价样本矩阵确定
邀请n名专家按照灰关系指标评估规则对底层m个指标进行打分,可得到评价样本矩阵Dm×n。
4.3 灰色评价数计算
假设U代表次层指标ui所组成的集合,记为U={u1,…,um}。ui为底层指标uij组成的子合集,记为ui={ui1,…,uin}。E代表评价专家打分Ek的合集,记为E={E1,…,El}。
则可定义评价专家打分属于灰类的评价数,具体公式见表达式(6)。

(6)
其中,dijk代表专家Ek对指标uij的打分;fe(dijk)代表dijk对应的灰类评价数。
依据表达式(6)可以得到底层指标的四类灰色评价数,例如最大需用过载指标得到的5名专家打分分别为5.0、4.5、5.0、4.5、5.0,则其四类灰色评价数如下:
X111=f1(5.0)+f1(4.5)+f1(5.0)+f1(4.5)+f1(5.0)=5
X112=f2(5.0)+f2(4.5)+f2(5.0)+f2(4.5)+f2(5.0)=4
X113=f3(5.0)+f3(4.5)+f3(5.0)+f3(4.5)+f3(5.0)=2
X114=f4(5.0)+f4(4.5)+f4(5.0)+f4(4.5)+f4(5.0)=0
4.4 灰色评价权向量及权矩阵计算
例如前文提到的最大需用过载指标示例,其灰色评价权向量为
r11=[5/11 4/11 2/11 0]
灰色评价权矩阵为灰色评价权向量的合集,具体为
R1=[r11r12r13r14r15r16r17]T
R2=[r21r22r23r24r25r26]T
R3=[r31]
4.5 综合指标评价
根据前文计算得到的灰色评价权矩阵R1、R2、R3与权重向量p,可得到顶层指标灰色评价结果计算公式见表达式(7)
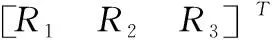
(7)
其中,C为各类评价灰类等级值向量,取值为C=[5.0,4.0,3.0,2.0]。
5 计算结果
为验证算法有效性,本文以爱国者-3防空导弹为研究对象,进行仿真验证。其中爱国者-3防空导弹采用公开数据建立其六自由度数学模型,拦截目标采用三自由度模型。
目标共选取五种运行模式,运动模式见表3。针对每种运动模式的目标进行1000条防空导弹拉偏弹道打靶,得到五种工况的仿真统计结果供性能评估使用。
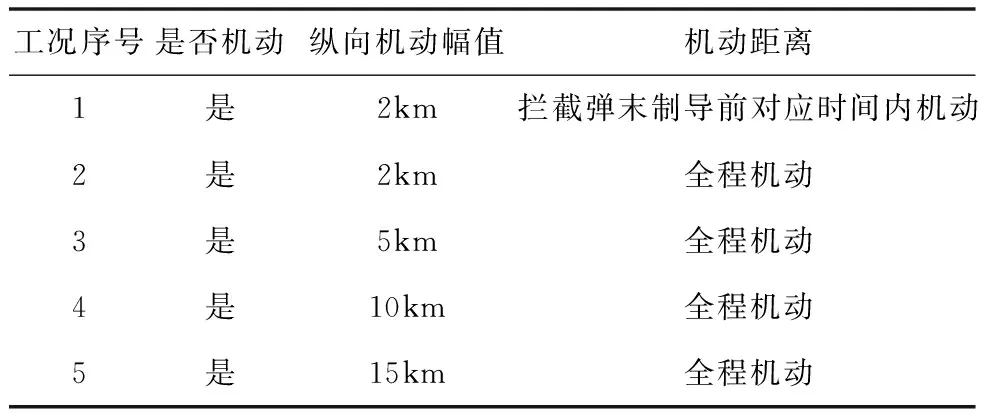
表3 目标机动模式
根据仿真结果进行如下计算分析。
5.1 指标打分
由于前文已经计算得到底层指标对顶层指标的权重向量,因此首先邀请5名专家对五条工况的14个底层指标仿真结果进行打分,得到的打分结果见表4。

表4 底层指标专家打分
其中,专家打分对应的指标次序按照图1从上往下排列,最大需用过载、最大航程、最大射高、技术实现难易程度为统计型或独立型数据,已通过其它遍历打靶或分析提前得到,因此每个专家针对这四项指标对应各个工况的打分均相同。
5.2 乘积计算评估值
乘积计算是一种常用的系统评估值计算方法,其原理为将底层指标对顶层指标的权重向量p与底层指标打分值向量Di直接相乘,即Zi=Di·pT,则可以计算得到5名专家的针对每条工况的打分情况见表5。

表5 乘积计算评估值
可见,由于每个专家的知识背景、对指标优劣的理解程度不同,导致专家的打分结果存在一定的差异。
前三条拦截效果较好的工况中,这种差异较小,可以使用平均值来作为系统的评估结果。但后两种拦截效果较差的工况中,专家之间的分歧过大(工况5中专家打分最大最小分值偏差比接近60%),显然无法将平均值作为评估结果;且工况5拦截效果明显不如工况4,但二者评分均为良好,与实际仿真结果不符,因此可以认为工况4、工况5评估失败。
5.3 灰关系系统评估
直接采用第4章中给出的灰关系系统评估法进行计算。可以计算得到五名专家的评估结果见表6。
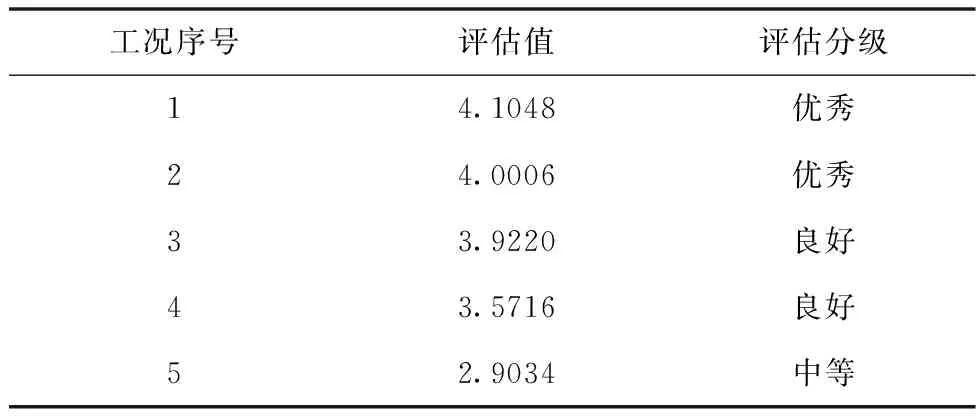
表6 灰关系系统评估值
由评估结果可知,前三条拦截效果较好的工况中,灰关系系统评估值与乘积计算评估值基本相同。而在后两条拦截效果较差的工况中,灰关系评估法通过将专家打分进行灰色分类,有效地中和了专家之间的打分差异,最终的评估结果也与实际仿真结果具有良好的符合性。
由此可见,灰关系系统评估法可以有效地综合多名评价专家的打分结果,针对各种工况,均可以给出合理的评估值,证明了该方法的合理性。
6 小结
本文以爱国者-3防空导弹为研究对象,首先建立了制导系统性能评估指标体系,之后采用了一种灰色系统理论与层次分析法相结合的评估方法进行性能评估,最后通过实际评估结果验证了该体系及评估方法的合理性。
